Basic Physics of Nuclear Medicine/Patient Dosimetry
This chapter overviews the MIRD method of estimating doses in nuclear medicine and gives results of surveys of typical patient doses for a small range of examinations. Doses from X-ray CT surveys are also given for comparison purposes, and to aid with your appreciation of the dosimetric impact of PET/CT and SPECT/CT.
MIRD Calculations
[edit | edit source]The direct measurement of the absorbed dose to organs of the body from nuclear medicine procedures is rarely possible. Most estimates depend on Monte Carlo simulation. To compute a dose distribution, many hundreds of thousands of virtual gamma rays originating in numerous source organs must be traced through the body as they interact with tissues by Compton scattering and photoelectric absorption. Contributions to the dose from Auger electrons, internal conversion electrons and beta decays must also be included This latter part of the simulation is usually quite straight-forward since these radiations can be considered to be absorbed in the organ they originate in.
The Medical Internal Radiation Dose (MIRD) Committee in the USA has provided a substantial body of data to assist in dose estimation. The MIRD method of calculation allows estimation of the dose to organs of significance from radioactivity distributed homogeneously throughout a particular source organ. The method can be split into two parts:
- Firstly, some assumptions are made about or measurements are taken of the biological distribution of radioactivity throughout the body, taking into account both the biological and physical half-life of the labelled radionuclide.
- The cumulated activity, Ãs, in any particular source organ is calculated by integrating the instantaneous activity over time. This data might be obtained from theoretical modelling (such as Compartmental Analysis) or from measurements using a gamma camera to measure the count rate as a function of time in the organ of interest - see the following figure:
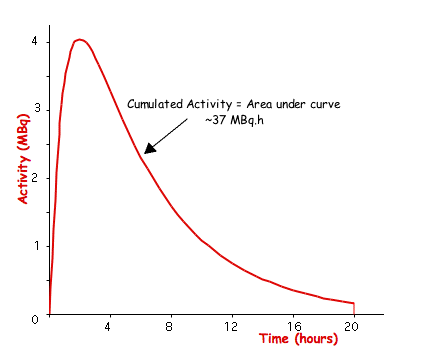
- Mathematically, this type of activity/time curve can be represented by the equation:
- where As(t) is the activity in the source organ, s at time, t.
- Secondly, the absorbed dose to a target organ, Dt, is calculated from:
- where the summation over s is intended to account for contributions from all source organs to the target organ. The S-factor, S(t,s) is the mean absorbed dose to the target organ, t, from unit activity of the relevant radioisotope distributed homogeneously within the source organ, s. Note that its possible for the source and target organ to be the same entity.
The S-Factor
[edit | edit source]The challenging part of the MIRD method is the calculation of the S-factor because it depends on accurate knowledge of the radiations emitted by the radionuclide. Although the MIRD publications assist by providing representative values of S-factors for most organs and for a variety of radionuclides, it is important to understand the methodology and hence the limitations of this technique.
The S-factor for each radiation type can be broken down into component factors:
where:
- D is a measure of the total energy associated with the particular radiation type and is a physical entity known from the radioisotope's decay scheme,
- f(t,s) is the absorbed fraction for the particular radiation emitted in the source organ, s, and absorbed by the target organ, t, and
- m is the mass of the target organ.
The absorbed fraction represents the fraction of the total energy emitted by radiation of a particular type that is absorbed in the target organ. For beta particles, which have a short range in tissue, it can be assumed that all the energy will be deposited in the source organ and other target organs will not be irradiated. That is:
Unless t = s, in which case:
The determination of the S-factor is very simple in this case.
For gamma-rays, however, no such simple approach is possible since the amount of energy deposited in the source organ and in the target organ is dependent on:
- the gamma ray energy, as well as
- the size, shape and separation of the two organs in question.
Furthermore, we need to take into account not just the gamma-rays from the nucleus of the radioisotope but also emissions from the whole atom, i.e. emissions resulting from the electron shells when stimulated by emissions from the nucleus. The situation for 99mTc is illustrated in the following table, as an example:
| Radiation | Radiations/Disintegration | Radiation Energy (keV) | Dose (keV/Disintegration) |
|---|---|---|---|
| Conversion electrons from M-shell, γ1 | 0.75 | 1.63 | 1.21 |
| γ2 | 0.89 | 140.5 | 125 |
| Conversion electrons from K-shell, γ2 | 0.09 | 119.5 | 10.6 |
| Conversion electrons from L-shell, γ2 | 0.01 | 137.5 | 1.47 |
| Conversion electrons from M-shell, γ2 | 0.002 | 140.0 | 0.27 |
| Conversion electrons from N- and outer shells, γ2 | 0.0004 | 140.4 | 0.05 |
| Conversion electrons from K-shell, γ3 | 0.006 | 121.6 | 0.67 |
| Conversion electrons from L-shell, γ3 | 0.002 | 139.6 | 0.24 |
| Conversion electrons from M-shell, γ3 | 0.0003 | 142.1 | 0.05 |
| Kα1 X-ray | 0.04 | 18.4 | 0.74 |
| Kα2 X-ray | 0.02 | 18.3 | 0.39 |
| Kβ X-ray | 0.01 | 20.6 | 0.25 |
| K-Auger electron | 0.02 | 15.5 | 0.32 |
| L-Auger electron | 0.1 | 2.2 | 0.22 |
We can see in the table that a range of radiations are generated within the atom as a whole. For instance, on the first line the energy of a gamma-ray emitted by the nucleus is given to an M-shell electron in about 75% of one type of isomeric transition giving it a maximum energy of 1.63 keV, i.e. about 1.2 keV per nuclear disintegration. On the second line, a gamma-ray resulting from another isomeric transition in 89% of instances emerges unscathed from the atom with an energy of 140.5 keV, or about 125 keV per disintegration. In a third case, in about 9% of these latter isomeric transitions, an electron in the K-shell gains energy of 119.5 keV, which is sufficient for it to overcome the binding energy (about 21 keV) of that shell and leave the atom. Notice that fluorescent X-rays, resulting from electronic transitions to fill vacancies in the K-shell are also produced - as well as Auger electrons.
Part of a resultant MIRD table of S-factors for 99mTc is reproduced below as examples of typical values:
| Target Organ | Liver as Source | Spleen as Source |
|---|---|---|
| Bladder Wall | 4.3 x 10-5 | 3.2 x 10-5 |
| Stomach Wall | 5.1 x 10-4 | 2.7 x 10-3 |
| Liver | 1.2 x 10-2 | 2.6 x 10-4 |
| Lungs | 1.4 x 10-4 | 6.2 x 10-4 |
| Pancreas | 1.1 x 10-3 | 5.1 x 10-3 |
| Spleen | 2.5 x 10-4 | 8.9 x 10-2 |
The unit of the S-factor is typically mGy/MBq/hour. Note that substantial discrepancies between actual and calculated values can be expected depending on differences in anatomy and physiological function between individual patients.
The Dose in a Liver Scan
[edit | edit source]To illustrate how the table above can be used in a hypothetical situation, suppose a liver scan is performed in which 37 MBq of 99mTc-labelled sulphur colloid is administered to a patient. Suppose also that it is found from metabolic modelling that:
- 80% of the cumulated activity goes to the patient's liver and
- 20% goes to their spleen.
When it is then assumed that the biological half-life for the colloid is infinite in these two organs, which is a reasonable approximation, the calculation of cumulated total activity is much simplified as illustrated in the box below:
Note that the liver dose arises almost exclusively from the presence of radioactivity in the liver and that the activity in the spleen contributes little to this dose - just 5%.
In similar way, the dose to the spleen can be calculated to be 5.8 mGy. Note that even though less activity accumulates in the spleen the absorbed dose is higher. This apparent paradox can be resolved however when you recall that the absorbed dose is the energy absorbed per unit mass.
The International Commission on Radiological Protection (ICRP) have published more accurate organ absorbed doses derived on the basis of knowledge of physiological data for what is known as the Reference Man and from the MIRD data. Note that the absorbed doses to the liver and to the spleen in the following table are 2.74 and 2.85 mGy, respectively - somewhat lower than we calculated in our simple, hypothetical situation above.
| Target Organ | wT | Absorbed Dose (mGy) | wT.HT (mSv) |
|---|---|---|---|
| Gonads (F) | 0.2 | 0.081 | 0.016 |
| Red Marrow | 0.12 | 0.41 | 0.049 |
| Colon | 0.12 | 0.07 | 0.008 |
| Lung | 0.12 | 0.2 | 0.024 |
| Stomach | 0.12 | 0.23 | 0.028 |
| Bladder | 0.05 | 0.04 | 0.002 |
| Breast | 0.05 | 0.1 | 0.005 |
| Liver | 0.05 | 2.74 | 0.137 |
| Oesophagus | 0.05 | 0.1 | 0.005 |
| Thyroid | 0.05 | 0.03 | 0.0015 |
| Bone Surfaces | 0.01 | 0.24 | 0.0024 |
| Spleen | 0.025 | 2.85 | 0.071 |
| Remainder | 0.05 | 0.21 | 0.005 |
Note that an effective dose of 0.35 mSv can be obtained by summing the values in the right hand column of the table.
Finally, note that a radiation weighting factor, wR, of unity has been assumed for simplicity throughout the above discussion for all the radiation energies arising from the decay of 99mTc.
Typical Nuclear Medicine Doses
[edit | edit source]The following table lists the effective dose from a number of nuclear medicine procedures (adapted from ICRP 53):
| Examination | Radiopharmaceutical | Activity (MBq) | Organ | Absorbed Dose (mGy) | Effective Dose (mSv) |
|---|---|---|---|---|---|
| Bone Scan | 99mTc-MDP | 740 | Bone Bladder |
46 38 |
4.2 |
| Heart Wall | 201Tl-Thallous Chloride | 120 | Testes Colon Kidney |
68 44 65 |
26(M) 16(F) |
| Infection | 67Ga-Gallium Citrate | 150 | Bone Colon Red Marrow Adrenal Glands Spleen |
94 25 31 14 15 |
15 |
| Renogram | 99mTc-DTPA | 150 | Bladder | 9.3 | 0.73 |
| Liver Scan | 99mTc-Sulphur Colloid | 74 | Liver Spleen |
5.2 5.6 |
0.7 |
| Lung-Perfusion | 99mTc-MAA | 74 | Lung Liver |
4.9 1.2 |
0.8 |
| Lung-Ventilation | 99mTc-Technigas | 20 | Lung | 2.2 | 0.3 |
| Thyroid Scan | 99mTc-Pertechnetate | 185 | Colon Stomach Thyroid |
8.0 4.8 4.1 |
1.9 |
| Thyroid Scan | 131I-Sodium Iodide | 150 | Bladder Stomach |
91 5 |
9.2 |
| PET Scan | 18F-2-Deoxyglucose | 180 | Bladder Heart |
29 11 |
3.4 |
Note that typical effective doses from 99mTc scans are of the order of a few mSv. Also note the high effective dose from a 201Tl scan - arising in part because of the high uptake of activity in the testes - and also those from 67Ga and 131I. The administered activities listed in the table are consistent with the most commonly used activities found in a survey of Australasian Nuclear Medicine practices conducted in 2000.
Typical Doses in X-Ray CT
[edit | edit source]The radiation dose delivered to the patient in X-ray CT is determined by factors which include the radiation energy and intensity characteristics, the size of the patient, the efficiency of the radiation detectors as well as factors derived from the specific form of image acquisition used (axial versus helical scanning, for example).
The absorbed dose is far from uniform within the patient - being greatest at the skin and a factor of about three lower in the centre of the irradiated region. Typical values for skin absorbed doses range from about 5 mGy to 50 mGy. Head scan absorbed doses are usually higher than body scan doses because of the substantial attenuation in the skull. In addition, the lens of the eye can receive a relatively large dose, typically 50 to 100 mGy, and if repeat examinations are undertaken the deterministic limit for cataract induction may be exceeded. Protocols, using appropriate gantry angulation, should be developed to minimise the possibility for direct irradiation of the eye. Likewise, relatively large uterine doses may arise from abdominal or pelvic CT scans and this may be a concern in scanning women of child bearing age.
A number of surveys have been published in recent years in which the effective dose from CT scans have been estimated - see the table below. The data indicates that the effective dose is typically 2 to 20 mSv with the higher values relating to CT scans of the abdomen and pelvis and the lower values relating to the head and cervical spine. This variation is largely a reflection of the number of radiosensitive organs that may be irradiated by the primary beam. The dose variation between countries is a different matter!
| Examination | New Zealand | Australia | United Kingdom |
|---|---|---|---|
| Head | 2.2 | 2.7 | 1.8 |
| Chest | 9.8 | 10.7 | 7.8 |
| Abdomen | 11.6 | 17.5 | 7.6 |
| Liver | 6.5 | 13.4 | 7.2 |
| Lumbar Spine | 5.0 | 5.4 | 3.3 |
| Pelvis | 7.2 | 11.2 | 7.1 |
Notice that effective doses from nuclear medicine procedures are of a similar order of magnitude, but generally lower, than that from CT examinations. To assist with your comparison: the effective dose from a chest X-ray is about 0.02 mSv, while that from a mammogram is about 0.4 mSv and from an intravenous pyelogram (IVP) its about 3 mSv. How does this last figure compare with the dose from a renogram? You might like to speculate on the reasons for the large difference as an exercise to further develop your understanding of this topic.
















