Basic Physics of Nuclear Medicine/Attenuation of Gamma-Rays

We covered the interaction of gamma-rays with matter from a descriptive viewpoint in the previous chapter and we saw that the Compton and Photoelectric Effects were the major mechanisms. We will consider the subject again here but this time from an analytical perspective. This will allow us to develop a more general understanding of the phenomenon.
Note that the treatment here also refers to the attenuation of X-rays since, as we noted before gamma-rays and X-rays are essentially the same physical entities.
Our treatment begins with a description of a simple radiation experiment which can be performed easily in the laboratory and which many of the early pioneers in this field did. We will then build on the information obtained from such an experiment to develop a simple equation and some simple concepts which will allow us generalise the situation to any attenuation situation.
Attenuation Experiment
[edit | edit source]The experiment is quite simple. It involves firing a narrow beam of gamma-rays at a material and measuring how much of the radiation gets through. We can vary the energy of the gamma-rays we use and the type of absorbing material as well as its thickness and density.
The experimental set-up is illustrated in the figure below. We refer to the intensity of the radiation which strikes the absorber as the incident intensity, I0, and the intensity of the radiation which gets through the absorber as the transmitted intensity, Ix. Notice also that the thickness of the absorber is denoted by x.
From what we covered in the previous chapter we can appreciate that some of the gamma-rays will be subjected to interactions such as the Photoelectric Effect and the Compton Effect as they pass through the absorber. The transmitted gamma-rays will in the main be those which pass through without any interactions at all.
We can therefore expect to find that the transmitted intensity will be less than the incident intensity, that is
But by how much you might ask. Before we consider this let us denote the difference between Ix and I0 as ∆I, that is
Effect of Atomic Number
[edit | edit source]- Let us start exploring the magnitude of ∆I by placing different absorbers in turn in the radiation beam. What we would find is that the magnitude of ∆I is highly dependent on the atomic number of the absorbing material. For example we would find that ∆I would be quite low in the case of an absorber made from carbon (Z=6) and very large in the case of lead (Z=82).
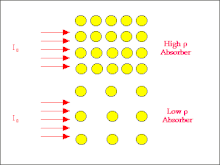
- We can gain an appreciation of why this is so from the following figure:

- The figure illustrates a high atomic number absorber by the large circles which represent individual atoms and a low atomic number material by smaller circles. The incident radiation beam is represented by the arrows entering each absorber from the left. Notice that the atoms of the high atomic number absorber present larger targets for the radiation to strike and hence the chances for interactions via the Photoelectric and Compton Effects is relatively high. The attenuation should therefore be relatively large.
- In the case of the low atomic number absorber however the individual atoms are smaller and hence the chances of interactions are reduced. In other words the radiation has a greater probability of being transmitted through the absorber and the attenuation is consequently lower than in the high atomic number case.
- With respect to our spaceship analogy used in the previous chapter the atomic number can be thought of as the size of individual meteors in the meteor cloud.
- If we were to precisely control our experimental set-up and carefully analyse our results we would find that:
- Therefore if we were to double the atomic number of our absorber we would increase the attenuation by a factor of two cubed, that is 8, if we were to triple the atomic number we would increase the attenuation by a factor of 27, that is three cubed, and so on.
- It is for this reason that high atomic number materials (e.g. Pb) are used for radiation protection.
Effect of Density
[edit | edit source]- A second approach to exploring the magnitude of ∆I is to see what happens when we change the density of the absorber. We can see from the following figure that a low density absorber will give rise to less attenuation than a high density absorber since the chances of an interaction between the radiation and the atoms of the absorber are relatively lower. In addition, the density determines the transmission coefficient as it relates to the sample, since the lower the density, the higher the transmission coefficient due to the porous nature of the material.
- So in our analogy of the spaceship entering a meteor cloud think of meteor clouds of different density and the chances of the spaceship colliding with a meteor.
Effect of Thickness
[edit | edit source]- A third factor which we could vary is the thickness of the absorber. As you should be able to predict at this stage the thicker the absorber the greater the attenuation.
Effect of Gamma-Ray Energy
[edit | edit source]- Finally in our experiment we could vary the energy of the gamma-ray beam. We would find without going into it in any great detail that the greater the energy of the gamma-rays the less the attenuation. You might like to think of it in terms of the energy with which the spaceship approaches the meteor cloud and the likelihood of a slow spaceship getting through as opposed to a spaceship travelling with a higher energy.
Mathematical Model
[edit | edit source]We will consider a mathematical model here which will help us to express our experimental observations in more general terms. You will find that the mathematical approach adopted and the result obtained is quite similar to what we encountered earlier with Radioactive Decay. So you will not have to plod your way through any new maths below, just a different application of the same form of mathematical analysis!
Let us start quite simply and assume that we vary only the thickness of the absorber. In other words we use an absorber of the same material (i.e. same atomic number) and the same density and use gamma-rays of the same energy for the experiment. Only the thickness of the absorber is changed.
From our reasoning above it is easy to appreciate that the magnitude of ∆I should be dependent on the radiation intensity as well as the thickness of the absorber, that is for an infinitesimally small change in absorber thickness:
the minus sign indicating that the intensity is reduced by the absorber.
Turning the proportionality in this equation into an equality, we can write:
where the constant of proportionality, μ, is called the Linear Attenuation Coefficient.
Dividing across by I we can rewrite this equation as:
So this equation describes the situation for any tiny change in absorber thickness, dx. To find out what happens for the complete thickness of an absorber we simply add up what happens in each small thickness. In other words we integrate the above equation. Expressing this more formally we can say that for thicknesses from x = 0 to any other thickness x, the radiation intensity will decrease from I0 to Ix, so that:
This final expression tells us that the radiation intensity will decrease in an exponential fashion with the thickness of the absorber with the rate of decrease being controlled by the Linear Attenuation Coefficient. The expression is shown in graphical form below. The graph plots the intensity against thickness, x. We can see that the intensity decreases from I0, that is the number at x = 0, in a rapid fashion initially and then more slowly in the classic exponential manner.
The influence of the Linear Attenuation Coefficient can be seen in the next figure. All three curves here are exponential in nature, only the Linear Attenuation Coefficient is different. Notice that when the Linear Attenuation Coefficient has a low value the curve decreases relatively slowly and when the Linear Attenuation Coefficient is large the curve decreases very quickly.

The Linear Attenuation Coefficient is characteristic of individual absorbing materials. Some like carbon have a small value and are easily penetrated by gamma-rays. Other materials such as lead have a relatively large Linear Attenuation Coefficient and are relatively good absorbers of radiation:
| Absorber | 100 keV | 200 keV | 500 keV |
|---|---|---|---|
| Air | 0.000195 | 0.000159 | 0.000112 |
| Water | 0.167 | 0.136 | 0.097 |
| Carbon | 0.335 | 0.274 | 0.196 |
| Aluminium | 0.435 | 0.324 | 0.227 |
| Iron | 2.72 | 1.09 | 0.655 |
| Copper | 3.8 | 1.309 | 0.73 |
| Lead | 59.7 | 10.15 | 1.64 |
The materials listed in the table above are air, water and a range of elements from carbon (Z=6) through to lead (Z=82) and their Linear Attenuation Coefficients are given for three gamma-ray energies. The first point to note is that the Linear Attenuation Coefficient increases as the atomic number of the absorber increases. For example it increases from a very small value of 0.000195 cm-1 for air at 100 keV to almost 60 cm-1 for lead. The second point to note is that the Linear Attenuation Coefficient for all materials decreases with the energy of the gamma-rays. For example the value for copper decreases from about 3.8 cm-1 at 100 keV to 0.73 cm-1 at 500 keV. The third point to note is that the trends in the table are consistent with the analysis presented earlier.
Finally it is important to appreciate that our analysis above is only strictly true when we are dealing with narrow radiation beams. Other factors need to be taken into account when broad radiation beams are involved.
Half Value Layer
[edit | edit source]As with using the Half Life to describe the Radioactive Decay Law an indicator is usually derived from the exponential attenuation equation above which helps us think more clearly about what is going on. This indicator is called the Half Value Layer and it expresses the thickness of absorbing material which is needed to reduce the incident radiation intensity by a factor of two. From a graphical point of view we can say that when:
the thickness of absorber is the Half Value Layer:

The Half Value Layer for a range of absorbers is listed in the following table for three gamma-ray energies:
| Absorber | 100 keV | 200 keV | 500 keV |
|---|---|---|---|
| Air | 3555 | 4359 | 6189 |
| Water | 4.15 | 5.1 | 7.15 |
| Carbon | 2.07 | 2.53 | 3.54 |
| Aluminium | 1.59 | 2.14 | 3.05 |
| Iron | 0.26 | 0.64 | 1.06 |
| Copper | 0.18 | 0.53 | 0.95 |
| Lead | 0.012 | 0.068 | 0.42 |
The first point to note is that the Half Value Layer decreases as the atomic number increases. For example the value for air at 100 keV is about 35 meters and it decreases to just 0.12 mm for lead at this energy. In other words 35 m of air is needed to reduce the intensity of a 100 keV gamma-ray beam by a factor of two whereas just 0.12 mm of lead can do the same thing. The second thing to note is that the Half Value Layer increases with increasing gamma-ray energy. For example from 0.18 cm for copper at 100 keV to about 1 cm at 500 keV. Thirdly note that relative to the data in the previous table there is a reciprocal relationship between the Half Value Layer and the Linear Attenuation Coefficient, which we will now investigate.
Relationship between μ and the HVL
[edit | edit source]As was the case with the Radioactive Decay Law, where we explored the relationship between the Half Life and the Decay Constant, a relationship can be derived between the Half Value Layer and the Linear Attenuation Coefficient. We can do this by using the definition of the Half Value Layer:
when
and inserting it in the exponential attenuation equation, that is:
to give
Therefore
and
These last two equations express the relationship between the Linear Attenuation Coefficient and the Half Value Layer. They are very useful as you will see when solving numerical questions relating to attenuation and frequently form the first step in solving a numerical problem.
Mass Attenuation Coefficient
[edit | edit source]We implied above that the Linear Attenuation Coefficient was useful when we were considering an absorbing material of the same density but of different thicknesses. A related coefficient can be of value when we wish to include the density, ρ, of the absorber in our analysis. This is the Mass Attenuation Coefficient which is defined as the:
The measurement unit used for the Linear Attenuation Coefficient in the table above is cm-1, and a common unit of density is the g cm-3. You might like to derive for yourself on this basis that the cm2 g-1 is the equivalent unit of the Mass Attenuation Coefficient.
Questions
[edit | edit source]Two questions are given below to help you develop your understanding of the material presented in this chapter. The first one is relatively straight-forward and will exercise your application of the exponential attenuation equation. The second question is a lot more challenging and will help you relate exponential attenuation to radioactivity and radiation exposure.
Question 1
How much aluminium is required to reduce the intensity of a 200 keV gamma-ray beam to 10% of its incident intensity? Assume that the Half Value Layer for 200 keV gamma-rays in Al is 2.14 cm.
Answer
- The question phrased in terms of the symbols used above is:
- We are told that the Half Value Layer is 2.14 cm. Therefore the Linear Attenuation Coefficient is
- Now combining all this with the exponential attenuation equation:
- we can write:
- Therefore
- So the thickness of aluminium required to reduce these gamma-rays by a factor of ten is about 7 cm. This relatively large thickness is the reason why aluminium is not generally used in radiation protection - its atomic number is not high enough for efficient and significant attenuation of gamma-rays.
- You might like to try this question for the case when Pb is the absorber - but you will need to find out the Half Value Layer for the 200 keV gamma-rays yourself!
- Here's a hint though: have a look at one of the tables above.
- And here's the answer for you to check when you've finished: 2.2 mm.
- In other words a relatively thin thickness of Pb is required to do the same job as 7 cm of aluminium.
Question 2
A 105 MBq source of 137Cs is to be contained in a Pb box so that the exposure rate 1 m away from the source is less than 0.5 mR/hour. If the Half Value Layer for 137Cs gamma-rays in Pb is 0.6 cm, what thickness of Pb is required? The Specific Gamma Ray Constant for 137Cs is 3.3 R hr-1 mCi-1 at 1 cm.
Answer
- This is a fairly typical question which arises when someone is using radioactive materials. We wish to use a certain quantity of the material and we wish to store it in a lead container so that the exposure rate when we are working a certain distance away is below some level for safety reasons. We know the radioactivity of the material we will be using. But its quoted in SI units. We look up a reference book to find out the exposure rate for this radioisotope and find that the Specific Gamma Ray Constant is quoted in traditional units. Just as in our question!
- So let us start by getting our units right. The Specific Gamma Ray Constant is given as:
- This is equal to:
- which is equal to:
- on the basis of the Inverse Square Law. This result expressed per becquerel is
- since 1 mCi = 3.7 x 107 Bq. And therefore for 105 MBq, the exposure rate is:
- That is the exposure rate 1 meter from our source is 891.9 mR hr-1.
- We wish to reduce this exposure rate according to the question to less than 0.5 mR hr-1 using Pb.
- You should be able at this stage to use the exponential attenuation equation along with the Half Value Layer for these gamma-rays in Pb to calculate that the thickness of Pb required is about 6.5 cm.
External Links
[edit | edit source]- Mucal on the Web - an online program which calculates x-ray absorption coefficients - by Pathikrit Bandyopadhyay, The Center for Synchrotron Radiation Research and Instrumentation at the Illinois Institute of Technology.
- Tables of X-Ray Mass Attenuation Coefficients - a vast amount of data for all elements from National Institute of Science & Technology, USA.