Associative Composition Algebra/Transcendental paradigm
In the ancient geometry of the circle, the relation between angle above the horizon and altitude of a star is called the sine function. Though a part of the nature of a circle, it is not an algebraic function in the sense of being expressible as a finite sequence of additions, subtractions, multiplications, divisions, powers or roots. Thus it is called a transcendental function. The invitation of this function "sine" into the polite company of algebraic manipulations required a fundamental innovation: a constant "base" b > 0 raised to a variable exponent: This innovation was used by Leonard Euler in his Introduction to the Analysis of the Infinite (1748). But the research that led to this development is due to a Jesuit trio: Gregoire de Saint-Vincent, A. A. de Sarasa, and Marin Mersenne working in the previous century. They tackled the ancient problem of quadrature of the hyperbola, a prominent issue since Archimedes had shown the quadrature of the parabola millennia before.
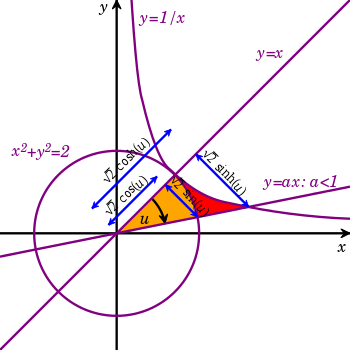
Consider first a unit square area. Then consider those rectangles that have the same area as the square. If x and y are the sides of such a rectangle, the graph of y = 1/x represents the rectangles {(0,0), (x,0), (0, 1/x), (x, 1/x)}. The rectangle with x = y = 1 is the unit square s. Now suppose b > a > 1 and (b, 1/b) is the corner of a rectangle h while (a, 1/a) is the corner of a rectangle g. The rectangles can be viewed as squeezed forms of one another: h is s squeezed by a, g is s squeezed by b. Then h can be re-inflated to s by a−1, so that g is obtained from h by squeezing with a−1b.
The squeezing operation corresponds to a positive real number p > 0. The squeeze is generally viewed with p > 1 so that x expands and y contracts, all the while area is preserved. This property of preservation of area, called equi-areal mapping, brings squeezing into contact with translations, rotations, and shear mappings which share the property. The squeeze is not part of classical kinematics but appears in special relativity as a re-linearization of velocity after the finitude of the speed of light exposes the non-linearity of classical velocity addition with vectors.
Note the axis of symmetry L: x = y of the hyperbola xy = 1. A point (x, 1/x) on the hyperbola determines a hyperbolic sector S(1,x) delimited by L, the hyperbola, and the line from (0,0) to the point. The perpendicular projection from the point to L establishes the hyperbolic sine, sinh v, where v is the area of the sector S(1,x), commonly called the hyperbolic angle. The foot of the projection determines cosh v by the length of the diagonal from (0,0) to the foot. In accord with a circle of area 2π, the sinh and cosh are normalized by a factor of √2.
Infinite series
[edit | edit source]Leonard Euler provided infinite series as an access point to the transcendental functions:
Look what happens when f is required to be its own derivative: the derivative of the nth term is
Given a0, where n! is the factorial. Take a0 = 1. Now which Euler computed to be 2.71828… and is now designated mathematical constant e.
The function f is known as the exponential function
Euler also broke the sum into even and odd terms: , where cosh takes the even terms, sinh the odd. The following lemma will be needed later.
Lemma:
proof: The odd terms of e−x turn negative, so they cancel in
- and add in
Now squaring and adding in the right hand side of the lemma yields
Exercises
[edit | edit source]- Use Euler's formula to show sine and cosine have alternating series.
- Using infinite series, show
- Exchange triangles of area 1/2 to show a hyperbolic sector has the same area as a dented trapezoid under the hyperbola and against its asymptote.
- What are the merits and demerits of calling a squeeze mapping a "hyperbolic rotation" ?
Sample
[edit | edit source]For a sample of AC algebra, the following is offered: Let A = (R2, xy) be the real plane with quadratic form xy. Further, let A be equipped with component-wise addition and multiplication, making it a real algebra. Denote N(x,y) = xy in this case. Then
Thus N is said to compose over the multiplication in A, and A might be called a composition algebra. However, in this text, AC algebras have an involution called a conjugation, written x*, used to define N by N(x) = x x*. Nevertheless, the algebra A constructed above is very closely related to split-binarions described in the next chapter. The split-binarions are a normalized form of A, where the multiplicative identity is a unit distance from the origin, and it has some formal correspondences with the complex field C. In A, the quadratic form can be interpreted as a weight, so that a transformation leaving it invariant is an isobaric transformation, a name used in 1999 by Peter Olver (Classical Invariant Theory, page 217) to describe a squeeze mapping.
Categorical treatment
[edit | edit source]In his essay "Cayley Algebras" included in a larger work published by American Mathematical Society (ISBN 978-0-8218-4459-5), Guy Roos presents a sequence of exercises which give a categorical expression of composition algebras. Say that A is a composition algebra over field K, so that it has a norm n: A → K and for every a, b in A, n(ab) = n(a) n(b). Composition algebras are sometimes non-commutative, so A is presumed to have non-commutative multiplication though the addition operation is commutative. The exercises culminate in showing a composition algebra is an alternative algebra. This property is connected with the associativity proposition a(bc)=(ab)c with three universal quantifiers, except that in alternative algebras only two quantifiers hold, meaning that a=b or b=c in the expression. In particular, when then the algebra is alternative.
Roos exercises
[edit | edit source]Definition: (a:b) = n(a+b) – n(a) – n(b)
- 2(ab:ab) = (a:a)(b:b)
- (ac:ad) = n(a)(c:d)
- (ac:bc) = (a:b) n(c)
- (ac:bd) + (ad:bc) = (a:b)(c:d)
- (aa:d) + n(a)(d:1) = (a:1)(a:d)
- (aa – (a:1)a + n(a)1 : d) = 0
- aa – (a:1)a + n(a) = 0
Definition: The trace of an element a is t(a) = (a:1)
As a unital algebra, 1 is in A, and A has a basis as a linear space. Write e = 1e as the basis element associated with the multiplicative identity, 1 or one (in oral communication).
Definition: The conjugate of a is a* = (a:e)e – a.
- (a*)* = a and n(a*) = n(a)
- a + a* = t(a)
- n(a) = a a*
- (a:b) = (a*:b*)
- (ac:d) + (ad:c) = ((a:1)c : d)
- (ad:c) + (a*c : d)
- (da:c) = (ca*:d)
- (ax:y) = (x:a*y) and (xa:y) = (x:ya*)
- (ab:1) = (a:b*) = (ba:1) so that t(ab) = t(ba)
- t((ab)c) = (ab:c*) = (a:c* b*) = (ca :b*) = t((ca)b)
- t((ab)c) = t(ca)b) = t(bc)a) = t(a(bc))
- (ab)* = b*a*
- For every c, ((ab)* :c) = (ab:c*) = (ca:b*) = (c:b*a*)
- (a:b)c = b*(ac) + a*(bc)
- For every d, (a:b)(c:d) = (b*(ac):d) + (a*(bc): d)
- (a:b)c = (ca)b* + (cb)a*
- n(a)c = a*(ac) = (ca)a*
- (a*a)c = a*(ac) and a+a* in K implies a2c = a(ac)
- (ca)a = ca2













