Artificial Neural Networks/Activation Functions
Activation Functions
[edit | edit source]There are a number of common activation functions in use with neural networks. This is not an exhaustive list.

Step Function
[edit | edit source]A step function is a function like that used by the original Perceptron. The output is a certain value, A1, if the input sum is above a certain threshold and A0 if the input sum is below a certain threshold. The values used by the Perceptron were A1 = 1 and A0 = 0.
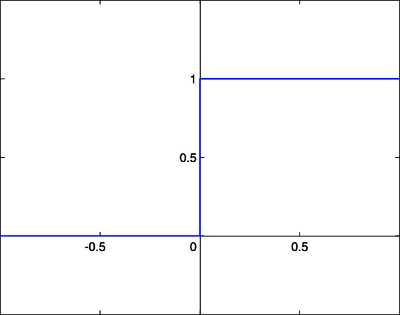
These kinds of step activation functions are useful for binary classification schemes. In other words, when we want to classify an input pattern into one of two groups, we can use a binary classifier with a step activation function. Another use for this would be to create a set of small feature identifiers. Each identifier would be a small network that would output a 1 if a particular input feature is present, and a 0 otherwise. Combining multiple feature detectors into a single network would allow a very complicated clustering or classification problem to be solved.
Linear combination
[edit | edit source]A linear combination is where the weighted sum input of the neuron plus a linearly dependent bias becomes the system output. Specifically:
In these cases, the sign of the output is considered to be equivalent to the 1 or 0 of the step function systems, which enables the two methods be to equivalent if
- .
Continuous Log-Sigmoid Function
[edit | edit source]A log-sigmoid function, also known as a logistic function, is given by the relationship:
Where β is a slope parameter. This is called the log-sigmoid because a sigmoid can also be constructed using the hyperbolic tangent function instead of this relation, in which case it would be called a tan-sigmoid. Here, we will refer to the log-sigmoid as simply “sigmoid”. The sigmoid has the property of being similar to the step function, but with the addition of a region of uncertainty. Sigmoid functions in this respect are very similar to the input-output relationships of biological neurons, although not exactly the same. Below is the graph of a sigmoid function.
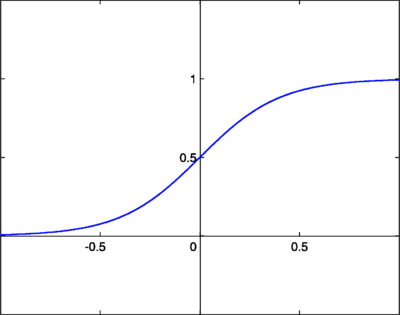
Sigmoid functions are also prized because their derivatives are easy to calculate, which is helpful for calculating the weight updates in certain training algorithms. The derivative when is given by:
When , using , the derivative is given by:
Continuous Tan-Sigmoid Function
[edit | edit source]Its derivative is:
ReLU: Rectified Linear Unit
[edit | edit source]The ReLU activation function is defined as:
It can also be expressed piecewise:

Its derivative is:
ReLU was first introduced by Kunihiko Fukushima in 1969 for representation learning with images, and is now the most popular activation function for deep learning. It has a very simple formula and derivative, making backpropagation calculations easier to calculate. As the output of the derivative function is always 1 for positive inputs, it suffers less from the gradient vanishing or exploding problem than other activation functions. ReLU does present the unique problem of "dying ReLU", where some nodes may very rarely activate or "die", providing no predictive power to the model. Variants of ReLU including Leaky and Parametric ReLU have been introduced to avoid the dying ReLU problem.
Softmax Function
[edit | edit source]The softmax activation function is useful predominantly in the output layer of a clustering system. Softmax functions convert a raw value into a posterior probability. This provides a measure of certainty. The softmax activation function is given as:
L is the set of neurons in the output layer.




![{\displaystyle {\frac {d\sigma (t)}{dt}}=\sigma (t)[1-\sigma (t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5cc22d67ef3f410413b2d68c6fb3091c06cc22)


![{\displaystyle {\frac {d\sigma (\beta ,t)}{dt}}=\beta [\sigma (\beta ,t)[1-\sigma (\beta ,t)]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a9a3b84b940e9843fbe5b55d281204acc91b6d3)





