Anatomy and Physiology of Animals/Nervous System

Objectives
[edit | edit source]After completing this section, you should know:
- the role of the nervous system in coordinating an animal’s response to the environment
- that the nervous system gathers, sorts and stores information and initiates movement
- the basic structure and functions of a neuron
- the structure and function of a synapse and neurotransmitter chemicals
- the nervous pathway known as a reflex with examples
- that training can develop conditioned reflexes in animals
- that the nervous system can be divided into the central and peripheral nervous systems
- that the brain is surrounded by membranes called meninges
- the basic parts of the brain and the function of the cerebral hemispheres, hypothalamus, pituitary, cerebellum and medulla oblongata
- the structure and function of the spinal cord
- that the peripheral nervous system consists of cranial and spinal nerves and the autonomic nervous system
- that the autonomic nervous system consists of sympathetic and parasympathetic parts with different functions
Coordination
[edit | edit source]Animals must be able to sense and respond to the environment in which they live if they are to survive. They need to be able to sense the temperature of their surroundings, for example, so they can avoid the hot sun. They must also be able to identify food and escape predators.
The various systems and organs in the body must also be linked so they work together. For example, once a predator has identified suitable prey it has to catch it. This involves coordinating the contraction of the muscle so the predator can run, there must then be an increased blood supply to the muscles to provide them with oxygen and nutrients. At the same time the respiration rate must increase to supply the oxygen and remove the carbon dioxide produced as a result of this increased activity. Once the prey has been caught and eaten, the digestive system must be activated to digest it.
The adjustment of an animal’s response to changes in the environment and the complex linking of the various processes in the body that this response involves are called co-ordination. Two systems are involved in co-ordination in animals. These are the nervous and endocrine systems. The first operates via electrical impulses along nerve fibres and the second by releasing special chemicals or hormones into the bloodstream from glands.
Functions of the Nervous System
[edit | edit source]The nervous system has three basic functions:
- 1. Sensory function - to sense changes (known as stimuli) both outside and within the body. For example the eyes sense changes in light and the ear responds to sound waves. Inside the body, stretch receptors in the stomach indicate when it is full and chemical receptors in the blood vessels monitor the acidity of the blood.
- 2. Integrative function - processing the information received from the sense organs. The impulses from these organs are analysed and stored as memory. The many different impulses from different sources are sorted, synchronised and co-ordinated and the appropriate response initiated. The power to integrate, remember and apply experience gives higher animals much of their superiority.
- 3. Motor function - The third function is the response to the stimuli that causes muscles to contract or glands to secrete.
All nervous tissue is made up of nerve cells or neurons. These transmit high-speed signals called nerve impulses. Nerve impulses can be thought of as being similar to an electric current.
The Neuron
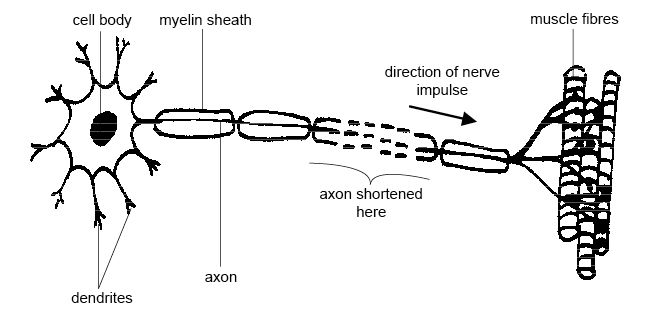
[edit | edit source]Neurons are cells that have been adapted to carry nerve impulses. A typical neuron has a cell body containing a nucleus, one or more branching filaments called dendrites which conduct nerve impulses towards the cell body and one long fibre, an axon, that carries the impulses away from it. Many axons have a sheath of fatty material called myelin surrounding them. This speeds up the rate at which the nerve impulses travel along the nerve (see diagram 14.1).
Diagram 14.1 - A motor neuron
The cell body of neurons is usually located in the brain or spinal cord while the axon extends the whole distance to the organ that it supplies. The neuron carrying impulses from the spinal cord to the hind leg or tail of a horse, for example, can be several feet long. A nerve is a bundle of axons.
A sensory neuron is a nerve cell that transmits impulses from a sense receptor such as those in the eye or ear to the brain or spinal cord. A motor neuron is a nerve cell that transmits impulses from the brain or spinal cord to a muscle or gland. A relay neuron connects sensory and motor neurons and is found in the brain or spinal cord (see diagrams 14.1 and 14.2).
Diagram 14.2 - The relationship between sensory, relay and motor neurons
Connections Between Neurons
[edit | edit source]The connection between adjacent neurons is called a synapse. The two nerve cells do not actually touch here for there is a microscopic space between them. The electrical impulse in the neurone before the synapse stimulates the production of chemicals called neurotransmitters (such as acetylcholine), which are secreted into the gap.
The neurotransmitter chemicals diffuse across the gap and when they contact the membrane of the next nerve cell they stimulate a new nervous impulse (see diagram 14.3). After the impulse has passed the chemical is destroyed and the synapse is ready to receive the next nerve impulse.
Diagram 14.3 - A nerve and magnification of a synapse
Reflexes
[edit | edit source]A reflex is a rapid automatic response to a stimulus. When you accidentally touch a hot object and automatically jerk your hand away, this is a reflex action. It happens without you having to think about it. Animals automatically blink when an object approaches the eye and cats twist their bodies in the air when falling so they land on their paws. (Please don’t test this one at home with your pet cat!).
Swallowing, sneezing, and the constriction of the pupil of the eye in bright light are also all reflex actions. Some other examples of reflex actions in animals can be shivering with cold and the opening of the mouth on hearing a sudden loud noise.
The path taken by the nerve impulses in a reflex is called a reflex arc. Most reflex arcs involve only three neurons (see diagram 14.4). The stimulus (a pin in the paw) stimulates the pain receptors of the skin, which initiate an impulse in a sensory neuron. This travels to the spinal cord where it passes, by means of a synapse, to a connecting neuron called the relay neuron situated in the spinal cord. The relay neuron in turn makes a synapse with one or more motor neurons that transmit the impulse to the muscles of the limb causing them to contract and remove the paw from the sharp object. Reflexes do not require involvement of the brain although you are aware of what is happening and can, in some instances, prevent them happening. Animals are born with their reflexes. You can think of them as being wired in.
Diagram 14.4 - A reflex arc
Conditioned Reflexes
[edit | edit source]In most reflexes the stimulus and response are related. For example the presence of food in the mouth causes the salivary glands to release saliva. However, it is possible to train animals (and humans) to respond to different and often quite irrelevant stimuli. This is called a conditioned reflex.
A Russian biologist called Pavlov carried out the classic experiment to demonstrate such a reflex when he conditioned dogs to salivate at the sound of a bell ringing. Almost every pet owner can identify reflexes they have conditioned in their animals. Perhaps you have trained your cat to associate food with the opening of the fridge door or accustomed your dog to the routines you go through before taking them for a walk.
Parts of the Nervous System
[edit | edit source]When we describe the nervous system of vertebrates we usually divide it into two parts (see diagram 14.5).
- 1. The central nervous system (CNS) which consists of the brain and spinal cord.
- 2. The peripheral nervous system (PNS) which consists of the nerves that connect to the brain and spinal cord (cranial and spinal nerves) as well as the autonomic (or involuntary) nervous system.
Diagram 14.5 - The nervous system of a horse
The Central Nervous System
[edit | edit source]The central nervous system consists of the brain and spinal cord. It acts as a kind of ‘telephone exchange’ where a vast number of cross connections are made.
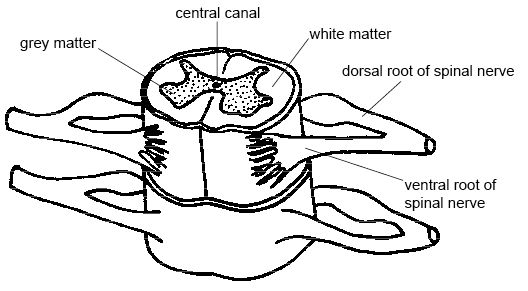
When you look at the brain or spinal cord some regions appear creamy white (white matter) and others appear grey (grey matter). White matter consists of masses of nerve axons and the grey matter consists of the cell bodies of the nerve cells. In the brain the grey matter is on the outside and in the spinal cord it is on the inside (see diagram 14.2).
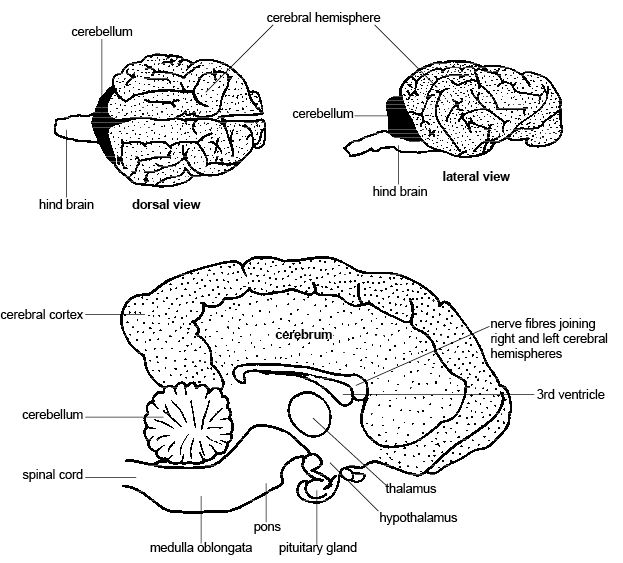
The Brain
[edit | edit source]The major part of the brain lies protected within the sturdy “box” of skull called the cranium. Surrounding the fragile brain tissue (and spinal cord) are protective membranes called the meninges (see diagram 14.6), and a crystal-clear fluid called cerebrospinal fluid, which protects and nourishes the brain tissue. This fluid also fills four cavities or ventricles that lie within the brain.
Brain tissue is extremely active and, even when an animal is resting, it uses up to 20% of the oxygen taken into the body by the lungs. The carotid artery, a branch off the dorsal aorta, supplies it with the oxygen and nutrients it requires. Brain damage occurs if brain tissue is deprived of oxygen for only 4–8 minutes.
The brain consists of three major regions:
- 1. the fore brain which includes the cerebral hemispheres, hypothalamus and pituitary gland;
- 2. the hind brain or brain stem, contains the medulla oblongata and pons and
- 3. the cerebellum or “little brain” (see diagram 14.6).
Diagram 14.6 - Longitudinal section through the brain of a dog
Mapping the brain
[edit | edit source]In humans and some animals the functions of the different regions of the cerebral cortex have been mapped (see diagram 14.7).
Diagram 14.7 - The functions of the regions of the human cerebral cortex
The Forebrain
[edit | edit source]The cerebral hemispheres are the masses of brain tissue that sit on the top of the brain. The surface is folded into ridges and furrows called sulci (singular sulcus). They make this part of the brain look rather like a very large walnut kernel. The two hemispheres are separated by a deep groove although they are connected internally by a thick bundle of nerve fibres. The outer layer of each hemisphere is called the cerebral cortex and this is where the main functions of the cerebral hemispheres are carried out.
The cerebral cortex is large and convoluted in mammals compared to other vertebrates and largest of all in humans because this is where the so-called “higher centres” concerned with memory, learning, reasoning and intelligence are situated.
Nerves from the eyes, ears, nose and skin bring sensory impulses to the cortex where they are interpreted. Appropriate voluntary movements are initiated here in the light of the memories of past events.
Different regions of the cortex are responsible for particular sensory and motor functions, e.g. vision, hearing, taste, smell, or moving the fore-limbs, hind-limbs or tail. For example, when a dog sniffs a scent, sensory impulses from the organ of smell in the nose pass via the olfactory (smelling) nerve to the olfactory centres of the cerebral hemispheres where the impulses are interpreted and co-ordinated.
In humans and some animals the functions of the different regions of the cerebral cortex have been mapped (see diagram 14.8).
Diagram 14.8 - The functions of the regions of the cerebral cortex
The hypothalamus is situated at the base of the brain and is connected by a “stalk” to the pituitary gland, the “master” hormone-producing gland (see chapter 16). The hypothalamus can be thought of as the bridge between the nervous and endocrine (hormone producing) systems. It produces some of the hormones that are released from the pituitary gland and controls the release of others from it.
It is also an important centre for controlling the internal environment of the animal and therefore maintaining homeostasis. For example, it helps regulate the movement of food through the gut and the temperature, blood pressure and concentration of the blood. It is also responsible for the feeling of being hungry or thirsty and it controls sleep patterns and sex drive.
The Hindbrain
[edit | edit source]The medulla oblongata is at the base of the brain and is a continuation of the spinal cord. It carries all signals between the spinal cord and the brain and contains centres that control vital body functions like the basic rhythm of breathing, the rate of the heartbeat and the activities of the gut. The medulla oblongata also co-ordinates swallowing, vomiting, coughing and sneezing.
The Cerebellum
[edit | edit source]The cerebellum (little brain) looks rather like a smaller version of the cerebral hemispheres attached to the back of the brain. It receives impulses from the organ of balance (vestibular organ) in the inner ear and from stretch receptors in the muscles and tendons. By co-ordinating these it regulates muscle contraction during walking and running and helps maintain the posture and balance of the animal. When the cerebellum malfunctions it causes a tremor and uncoordinated movement.
The Spinal Cord
[edit | edit source]The spinal cord is a cable of nerve tissue that passes down the channel in the vertebrae from the hindbrain to the end of the tail. It becomes progressively smaller as paired spinal nerves pass out of the cord to parts of the body. Protective membranes or meninges cover the cord and these enclose cerebral spinal fluid (see diagram 14.9).
Diagram 14.9 - The spinal cord
If you cut across the spinal cord you can see that it consists of white matter on the outside and grey matter in the shape of an H or butterfly on the inside.
The Peripheral Nervous System
[edit | edit source]The peripheral nervous system consists of nerves that are connected to the brain (cranial nerves), and nerves that are connected to the spinal cord (spinal nerves). The autonomic nervous system is also part of the peripheral nervous system.
Cranial Nerves
[edit | edit source]There are twelve pairs of cranial nerves that come from the brain. Each passes through a hole in the cranium (brain case). The most important of these are the olfactory, optic, acoustic and vagus nerves.
The olfactory nerves - (smell) carry impulses from the olfactory organ of the nose to the brain.
The optic nerves - (sight) carry impulses from the retina of the eye to the brain.
The auditory (acoustic) nerves - (hearing) carry impulses from the cochlear of the inner ear to the brain.
The vagus nerve - controls the muscles that bring about swallowing. It also controls the muscles of the heart, airways, lungs, stomach and intestines (see diagram 14.5).
Spinal Nerves
[edit | edit source]Spinal nerves connect the spinal cord to sense organs, muscles and glands in the body. Pairs of spinal nerves leave the spinal cord and emerge between each pair of adjacent vertebrae (see diagram 14.9).
The sciatic nerve is the largest spinal nerve in the body (see diagram 14.5). It leaves the spinal cord as several nerves that join to form a flat band of nervous tissue. It passes down the thigh towards the hind leg where it gives off branches to the various muscles of this limb.
The Autonomic Nervous System
[edit | edit source]The autonomic nervous system controls internal body functions that are not under conscious control. For example when a prey animal is chased by a predator the autonomic nervous system automatically increases the rate of breathing and the heartbeat. It dilates the blood vessels that carry blood to the muscles, releases glucose from the liver, and makes other adjustments to provide for the sudden increase in activity. When the animal has escaped and is safe once again the nervous system slows down all these processes and resumes all the normal body activities like the digestion of food.
The nerves of the autonomic nervous system originate in the spinal cord and pass out between the vertebrae to serve the various organs (see diagram 14.10).There are two main parts to the autonomic nervous system—the sympathetic system and the parasympathetic system.
The sympathetic system stimulates the “flight, fright, fight” response that allows an animal to face up to an attacker or make a rapid departure. It increases the heart and respiratory rates, as well as the amount of blood flowing to the skeletal muscles while blood flow to less critical regions like the gut and skin is reduced. It also causes the pupils of the eyes to dilate. Note that the effects of the sympathetic system are similar to the effects of the hormone adrenaline (see Chapter 16).
The parasympathetic system does the opposite to the sympathetic system. It maintains the normal functions of the relaxed body. These are sometimes known as the “housekeeping” functions. It promotes effective digestion, stimulates defaecation and urination and maintains a regular heartbeat and rate of breathing.
Diagram 14.10 - The function of the sympathetic and parasympathetic nervous systems
Summary
[edit | edit source]- The neuron is the basic unit of the nervous system. It consists of a cell body with a nucleus, filaments known as dendrites and a long fibre known as the axon often surrounded by a myelin sheath.
- A nerve is a bundle of axons.
- Grey matter in the brain and spinal cord consists mainly of brain cells while white matter consists of masses of axons.
- Nerve Impulses travel along axons.
- Adjacent neurons connect with each other at synapses.
- Reflexes are automatic responses to stimuli. The path taken by nerve impulses involved in reflexes is a reflex arc. Most reflex arcs involve 3 neurons - a sensory neuron, a relay neuron and a motor neuron. A stimulus, a pin in the paw for example, initiates an impulse in the sensory neuron that passes via a synapse to the relay neuron situated in the spinal cord and then via another synapse to the motor neurone. This transmits the impulse to the muscle causing it to contract and remove the paw from the pin.
- The nervous system is divided into 2 parts: the central nervous system, consisting of the brain and spinal cord and the peripheral nervous system consisting of nerves connected to the brain and spinal cord. The autonomic nervous system is considered to be part of the peripheral nervous system.
- The brain consists of three major regions: 1. the fore brain which includes the cerebral hemispheres (or cerebrum), hypothalamus and pituitary gland; 2. the hindbrain or brain stem containing the medulla oblongata and 3. the cerebellum.
- Protective membranes known as the meninges surround the brain and spinal cord.
- There are 12 pairs of cranial nerves that include the optic, olfactory, acoustic and vagus nerves.
- The spinal cord is a cable of nerve tissue surrounded by meninges passing from the brain to the end of the tail. Spinal nerves emerge by a ventral and dorsal root between each vertebra and connect the spinal cord with organs and muscles.
- The autonomic nervous system controls internal body functions not under conscious control. It is divided into 2 parts with 2 different functions: the sympathetic nervous system that is involved in the flight and fight response including increased heart rate, bronchial dilation, dilation of the pupil and decreased gut activity. The parasympathetic nervous system is associated with decreased heart rate, pupil constriction and increased gut activity.
Worksheet
[edit | edit source]Test Yourself
[edit | edit source]1. Add the following labels to this diagram of a motor neuron.
- cell body | nucleus | axon | dendrites | myelin sheath | muscle fibres
2. What is a synapse?
3. What is a reflex?
4. Rearrange the parts of a reflex arc given below in the order in which the nerve impulse travels from the sense organ to the muscle.
- sense organ | relay neuron | motor neuron | sensory neuron | muscle fibres
5. Add the following labels to the diagram of the dog’s brain shown below.
- cerebellum | cerebral hemisphere | cerebral cortex | pituitary gland | medulla oblongata
6. What is the function of the meninges that cover the brain and spinal cord
7. Give 3 effects of the action of the sympathetic nervous system.
Websites
[edit | edit source]- http://en.wikipedia.org/wiki/Neuron Wikipedia. Lots of good information here but as usual a warning that there are terms and concepts that are beyond the scope of this course. Also try ‘reflex action’ ; ‘autonomic nervous system’ ;
- http://images.google.co.nz/imgres?imgurl=http://static.howstuffworks.com/gif/brain-neuron.gif&imgrefurl=http://science.howstuffworks.com/brain1.htm&h=296&w=394&sz=17&hl=en&start=5&tbnid=LWLRI9lW_5PZhM:&tbnh=93&tbnw=124&prev=/images%3Fq%3Dneuron%26svnum%3D10%26hl%3Den%26lr%3D%26sa%3DN How Stuff Works. This site is for the neuron but try ‘neuron types’, ‘brain parts’ and ‘balancing act’ too.
- http://web.archive.org/web/20060821134839/http://www.bbc.co.uk/schools/gcsebitesize/flash/bireflexarc.swf Reflex Arc. Nice clear and simple animation of a reflex arc.