Aeroacoustics/Acoustic Sources
Introduction
[edit | edit source]All normal material bodies, such a solids and gases, obey the mass continuity equation. In rectangular coordinates it can be expressed using several symbol methods
Essentially, the right side of the equation accounts for the mass inflow/outflow rate in a small volume. If the sum is zero, the density does not change with time. The material is considered incompressible and the signal propagation speed is infinite. Any local action is transferred instantly to all other locations. All materials have a degree of compressibility and so the density changes with time and have a finite propagation speed. Any local action takes a certain amount of time to reach remote locations so all descriptive equations must incorporate a time delay factor. Since the concern here is Aeroacoustics, the propagation speed is determined by several factors associated with the properties of gases. The motion of gases is governed by the above equation as well as by the momentum equation which relates fluid response to the several forces; this equation is nonlinear.
If a number of simplifying assumptions are made, the linear acoustical wave equation can be extracted from it.
Here it is expressed in terms of density changes and is tied to a constant fluid density and a constant propagation speed called the sound speed; these are denoted by the subscript 0. That speed is based on all the physical changes being quite small. If it is not, the propagation speed is higher and results in the well known phenomenon of shock waves. The developments here will separate the regions by a boundary beyond which the wave equation applies. This equation is for wave propagation and does not contain a source term. A pioneering work by Lighthill [1] reformulated these equations to separate out the region where the wave equations applies from the region where the sound field is embedded in the source motion. The equation below shows that separation in terms of a stress tensor .
There are a number of articles that show the general solution to that equationAeroacoustics[2][3] One form is shown in the equation below[4]
The variable r is the distance from the source region y to the far field position x. The square brackets imply the time delay factor associated with that position. The first term refers to the entire stress tensor and is related to a distribution of quadrupoles. The second term is related to the momentum or force exerted on the acoustic medium and is related to a distribution of dipoles. The last term is associated with mass flux and is related to a distribution of monopoles. What this equation says is that there are only three basic types of sound sources. In this article, these source are addressed as single sources rather than a distribution of sources, to uncover their basic characteristics. As will be shown below, and as suggested in the equation above, the dipole can be considered as a space derivative on the monopole, while the quadrupole can be considered a double derivative of the monopole. It has been found that if the wave equation is expressed in terms of a velocity potential , all the physical variables can be derived from it.
Monopole
[edit | edit source]Assume that we have a source at point which generates some volumetric expansion or contraction. The corresponding wave equation for such case is
Using the free space Green's function that was introduced before [1] , the velocity potential will be
The above solution looks like the following picture if the source is located at the origin. As you can see this type of source generates symmetric spherical waves. This omni-direction source is called a monopole.
Theory
[edit | edit source]The general theory noted above includes a source term that describes the motion that results in the sound field. It can be a single source or a distribution of sources with known characteristics (Lighthill). Below, the source is addressed as a black box by being enclosed within a spherical boundary beyond which the acoustic wave equation is valid. From that, the nature of the source is deduced from the motion in the acoustic medium. In this specific case, we are concerned only with spherically symmetric acoustic motion associated with a single monopole source. The wave equation for this can be described in the form
The symbol φ is called the velocity potential from which most of the physical variables can be derived such as pressure or velocity. The letter F represents an arbitrary function. Analysis of the dimensions suggests that Q have the dimensions of which can be interpreted as an oscillatory volumetric flow rate. When the intensity of the field is integrated over a sphere, the sound power W can be expressed in a fundamental way as
Z0 is the characteristic impedance of the medium into which the sound is propagated. The sound power of a monopole can be interpreted as the mean square of the time rate of change of the mass flow rate M. This relationship applies to any fluctuating flow rate, whether random or periodic. Of most interest is periodic motion at a prescribed frequency. It is described by a radian frequency ω=2πf, where f is the frequency in Hertz. Often the relationships for a point monopole are developed, but the solution blows up as the source point is approached if the source function is omitted. This is not a handicap if a monopole with finite radius a (a pulsating sphere) is described. Two useful relationships are this case are
Where a represents the sphere radius and ua represents the radial velocity on the surface. The solution of the wave equation for the sound pressure can be shown in the form
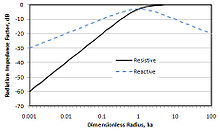
The symbol k is called the wave number despite the fact that it has the dimensions of reciprocal length. When combined with a distance, such as r, it is interpreted as a distance expressed in wavelengths. The pressure term in square brackets has a complex variable in it. This is due to two types of motion: reactive and resistive. The reactive motion can be considered incompressible; the pressure is at quadrature to the velocity so no work is done on the medium. The resistive motion represents the compressible motion that does work on the medium and radiates energy away from the source. Most sound measurements are made sufficiently far from the source that only the resistive, or sound, pressure is measured. That distance is called the far field, while the distance in which the reactive motion dominates is called the near field. The boundary between the two fields increases with the strength of the source and decreases with the frequency. The square bracketed term in the pressure equation is composed of two components, the resistive R and reactive X radiation impedance seen by the monopole. The two lower equations below are the expressions for them. The figure on the right shows the two forms of impedance as a function of dimensionless frequency. Very close to the source in wavelengths (low frequencies), most of the motion is incompressible and very little of the energy input is radiated away as sound. Loudspeaker designers increase the source strength at those frequencies to flatten the overall frequency response. At higher frequencies, monopoles radiate sound very efficiently. For a single frequency finite monopole, the sound power can be expressed in a simple way
A is the surface area of the sphere at radius a, and R is the resistive radiation impedance at the surface of the sphere.
Interaction of two Monopoles
[edit | edit source]
When a monopole is a distance h above a hard reflecting plane, an image source appears at the same distance below the surface. The sound power expression must account for the time delay associated with the reflection. The equation for that is
The additional term accounts for the constructive/destructive interference effects. As the distance from the surface approaches zero, the sound power is increased by 4 (6 dB). An example of interference effects is shown in the figure on the right; the graph shows the sound pressure level in the right quadrant above the plane. A monopole was located 10 inches above a hard reflecting surface and was radiating at 500 Hz. Destructive interference occurs at about 45 degrees from the origin. The blue arc represents a uniform monopole field. In the more general case, there are two monopoles in proximity to each other. The second source can have an output and phase that is different from the first. An interesting case is when the source size and frequency of each is the same. For this case the sound power equation becomes



The symbols u1 and u2 represent the surface velocities of the two sources, and the letter δ represents the phase difference between the two. An example is shown in the figure on the right of the combined sound pressure level of two monopoles radiating at 1000 Hz and separated by 72 cm with a 180 degree phase shift between them. Note that the sound level on the plane between them is minimized by the phase opposition.
Monopole-like Sound Sources
[edit | edit source]Very few real world sound sources are close approximations to the theoretical one. One example is largest monopole that has ever existed. It was the 57 Megaton hydrogen bomb exploded over Novaya Zemlya Island in the Soviet Union.[5] This extreme example points out the fact that the radius of the acoustic source must be at, or beyond, the boundary where the wave equations applies. In this case the source size must have a radius of several miles and the activity within that radius that generates the oscillatory mass flow rate is more like a black box from the acoustical viewpoint. Another example on the other side of the size scale is combustion in a propane burner with turbulent flow. As the gas transverses the flame front, the expansion creates a number of tiny monopole sound sources. Measurements of sound spectra were made at a number of angular positions. The results are shown in the figure on the right. There was essentially no difference between the on-axis spectrum and the 170 degree spectrum. Refraction effects changed the spectrum at other angles. There are numerous sound sources that are what may be called monopole-like. The similarity to the theoretical monopole lies in the fact that there is a variable mass flow creating the sound field. The difference is that solid boundaries are integral to the source as opposed to being just nearby. One example is a piston in a plane surface; the theory has been worked out.[6] At wavelengths large with respect to piston diameter (ka small), the sound field is radially symmetric. At shorter wavelengths, radiation from one part of the piston may cause destructive interference with that from another part, resulting in lobe patterns. The same applies to sound created by a piston in a sphere,[7] a loudspeaker at the end of a cylinder or sound radiated from the exit of a cylindrical duct. These are cases where the wave equation applies at the source boundary. There are other cases where the variable volumetric flow rate is associated with a mean flow. A classic example is the sound from the Vergeltungswaffe Eins (V1, buzz bomb) of World War II. The V1 flying bomb operated as a pulse jet and created a significant sound field at frequencies near 100 Hz. The directivity of the sound field has been measured and is shown in the figure on the right. During the exhaust phase, the duct inlet door was closed, so no forward radiation was created. This example highlights another important aspect of the monopole-like sound source. One would expect the sound field to be reasonably uniform at such low frequencies, (ka=0.27), but it is not. The exit plane of the pulsating exit flow, unlike the earlier examples, is not a boundary where the acoustical wave equation applies but is imbedded in a high velocity jet flow.
There is another category of monopole-like sound sources called aerodynamic whistles.[8] They are devices in which the sound created feeds back to the fluid motion to create an instability that is amplified. These whistles have symmetric flow oscillation that can result in vortex rings which impinge on a solid resulting in sound generation. Examples are the tea pot whistle, the Hartmann and Galton whistle, and the corrugated pipe tone. They are all associated with mean flows unlike the theoretical model.
Scaling Monopole Sources
[edit | edit source]Geometric and dynamic similarity are important when comparing different modes of operation and size for the same source type. The geometry is described by a dimension L and the dynamics are described by a speed U. If these values are chosen properly, they become characteristic of the device. They can be used to determine the change in sound power if the device is changed in size or speed. The first equation below is that for a point monopole at a discrete frequency. The volumetric flow rate term can be replaced by a dimensionless version and the frequency can be replaced by the dimensionless Strouhal number. This number was developed by Vincenz Strouhal while studying vortex shedding from cylinders. He found it to be relatively constant over a range of flow speeds (near 0.2). The Strouhal number can now be deduced directly by making the mass continuity equation dimensionless. If these two dimensionless values are inserted in the sound power equation, the last equation results. For many sound sources, both dimensionless parameters are relatively constant, so the sound power rises with the fourth power of the characteristic speed and the second power of the characteristic length.[9] This relationship has been confirmed with many sound sources from automobile tire noise to a variety of whistle mechanisms.


A good example of the applicability of the latter equation is motor vehicle sound. The upper figure on the right shows the sound pressure level measured at 50 feet from a variety of automobiles at several speeds.[10] The dashed line is the speed law, strongly suggesting the monopole nature of the radiation. For most well maintained vehicles, the major sources are the variable volumetric exhaust sound and tire sound. The source of tire sound had been a question for a number of years. Data for vehicles with little exhaust sound showed that at 60 mph the maximum spectrum level occurred near 1000 Hz. If a value of 0.2 is used for the Strouhal number, it is possible to estimate that the characteristic length was on the order of ¼ inch; tire tread pumping. Further corroboration was obtained by measuring the sound spectrum of an automobile with a quiet exhaust at a fixed distance at two vehicle speeds (30 and 60 mph).[11] The two spectra are compared in the figure on the right. The lower speed spectrum was as measured. The measured higher speed spectrum was reduced by 12 dB using the monopole speed law and the frequency spectrum was shifted down by one octave based on a constant Strouhal number. The frequency maxima compare closely. The close comparison suggests that the Strouhal number and the dimensionless volumetric flow rate was relatively constant. It need not be. The wave equation used here does not include a viscous term. In the far sound field, it has only a minor effect, but close to the source, particularly a fluid mechanical one, it can be important. Viscous effects are characterized by the Reynolds number and the two dimensionless factors can have a weak dependence on that number.
Dipole
[edit | edit source]A dipole is a source which appears in the wave equation as
Theory
[edit | edit source]The equation for a dipole, unlike the monopole, has two directions, the radius from the source and one angle. The equation for the acoustic motion outside the source can be expressed in these coordinates as
An outgoing solution of the wave equation is
This result can be obtained by differentiating the monopole velocity potential in a specific direction.
In a sense, a dipole is two merging monopoles aligned in that specific direction. The dimension of Q in this case is When the radial velocity is integrated over the sphere, it is found that the net volumetric flow rate is zero. When the component of pressure in a specific direction is integrated over the sphere a non-zero force results. When the component of pressure at right angles to the specific direction is integrated over the sphere, there is a zero result. The force F in the z direction (θ=0) is related to the Q variable as The velocity potential can now be expressed in terms of the applied force as
Similar to the monopole development, the sound power of a dipole can be expressed in terms of applied force in a fundamental way as
The sound power can be interpreted as the mean square of the time rate of change of a force applied to the medium in a specific direction.
Of most interest is a rigid sphere of radius a vibrating at a specific frequency in the z direction. (a finite sized dipole). The various fields are
The intensity has two components. The radial intensity has both a resistive and reactive component, while the angular intensity has only a reactive component. This suggests that the motion stores more incompressible energy in the field than the monopole. The figure on the right shows the directivity pattern that results.

The sound power of a finite dipole is
The radiation impedance of a finite dipole is

The reactive impedance of the dipole at low frequencies is considerably higher than that for a monopole suggesting the large amount of stored energy in the incompressible field. The resistive impedance at low frequencies is much lower that for the monopole suggesting the radiation inefficiency at these frequencies.
Interaction of Two Dipoles
[edit | edit source]When a dipole is a distance h above a hard reflecting surface, an image source appears at the same distance below the surface. Unlike the monopole, the orientation of the force vector must also be accounted for as well as the time delays associated with the reflection. The equation for the mean square sound pressure is


Because the reflection force vector direction is a mirror image of the source vector there are two angles to be accounted for. Examples of the influence of this cumbersome equation are given in the figures. In the first example, on the left, the dipole is oriented vertically with respect to a horizontal surface and radiating at 1000 Hz. The source is 20 cm above the surface, so destructive interference occurs and the standard dipole directivity is modified. The second figure, on the right, is when the dipole axis is horizontal; other conditions being the same. The more general case of two interacting dipoles at arbitrary magnitudes, frequencies, angles, and phase differences can be formulated but are not much more illuminating.
Dipole-like Sound Sources
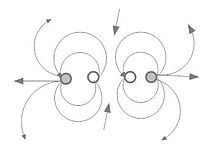
[edit | edit source]There are few sources that are close approximations to the theoretical dipole; most may be called dipole-like. The similarity is in the sound field created. The difference lies in the process by which the sound field is created. In actual situations, the force that drives the sound field is created by fluctuating momentum due to interaction of a flow with a solid object. Although the monopole source is clearly related to density variations, in real dipole situations the density variations can be buried in a flow field that can be treated as incompressible to make analysis progress. The theory of vortex sound was developed to handle this situation[12][13][14][15] The left figure shows the flow field around two monopoles of opposite phase. The center figure shows the flow field around a horizontally oscillating rigid sphere and the right figure shows the flow field around two vortices of opposite rotation.



A classic example of vortex flow is the Aeolian tone created by flow over a cylinder Vortices are alternatively shed from the cylinder. The figure on the left shows two phases of coherent vortex shedding from a cylinder (dark circle). The oscillating circulation around the cylinder results in a force that generates a dipole-like sound field. Unlike the theoretical dipole, the asymmetry results in a lift dipole perpendicular to the flow and a drag dipole parallel to the flow. It was this phenomenon that Vincenz Strouhal studied.[16]]. Philips[17] analyzed the fluid motion around the cylinder as if it were incompressible. Unlike the theoretical model, the cylinder does not move, only the fluid. Experiments have been performed on an unstable circular jet impinging on a downstream ring.[18] The jet instability resulted in a ring vortex impinging on a fixed physical ring. A sequential diagram is shown in the center figure It is circular version of the Aeolian tone. The sound field was clearly a dipole caused by the vortex circulation around the ring. Another example is the exhaust flow from pipe. At low speeds, the fluctuations in the flow rate create a monopole-like sound field. At much higher speeds, the vortex model shown in the figure on the right becomes applicable. A dipole sound field is created by the ring vortex acting at the pipe edge. materials. Powell had this to say about vortex sound: Because in a free flow there can be no change of the total vortex strength (circulation times area), there is no net dipole strength, but each moving element of vorticity still causes local dipole-like flow. A cardinal result is that the vorticity in a slightly compressible fluid can be considered to induce the whole flow field, both the hydrodynamic part and the acoustic part.



Scaling Dipole Sources
[edit | edit source]Geometric and dynamic similarity is important when comparing different modes of operation and size for the same source type. The geometry is described by a dimension L and the dynamics are described by a speed U. If these values are chosen properly, they become characteristic of the device. They can be used to determine the change in sound power if the device is changed in size or speed. The first equation below is that for a point dipole at a discrete frequency. The fluctuating force can be replaced by a dimensionless version and the frequency can be replaced by the dimensionless Strouhal number. If these dimensionless values are inserted in the sound power equation the last equation results. For many dipole sound sources, both dimensionless parameters are relatively constant, so the sound power rises with the sixth power of the characteristic speed and the second power of the characteristic length. This relationship has been confirmed with many actual sound sources.

The vortex whistle is the result of a precessing swirl flow at a tube exit.[19][20] A rotating dipole sound field has been measured. The rotating force vector was also deduced and was found to depend on the square of the swirl speed suggesting the dimensionless force was nearly constant. The aeolian tone tests of Strouhal demonstrated that his number can be nearly constant, so the U6 law would be expected in many cases. The edge tone is another example.[21] Turbulent flow over a flat plate or laminar flow over an airfoil is known to create nearly pure tones at the trailing edge of the surface. In one test[22] the tone frequency, the mean flow speed and the boundary layer thickness was combined to create a Strouhal number of 0.21. In the same tests the broad band spectra at a number of flow speeds were frequency and level scaled using the above dipole relationships to produce the figure on the right. The close fit suggests that trailing edge sound is of dipole nature.
Quadrupoles
[edit | edit source]A quadruple is a source distribution involving two space derivatives
An acoustic field generated by a point lateral quadrupole is shown below. Notice the angle of maximum sound level.
General Theory
[edit | edit source]The equation for a quadrupole, unlike the dipole and monopole, has three directions, the radius from the source and two angles. The equation can be expressed in spherical coordinates where the linear equations are valid as

The monopole is scalar, the dipole is a vector, while the quadrupole is a second order tensor. The dipole can be considered as two close monopoles out of phase with each other. The quadrupole can be considered as two close dipoles whose force vectors are in opposite directions or four monopoles oriented as shown in the figure eon the right. A lateral quadrupole is one where the force vectors are parallel to, but lateral to each other. As suggested in the figure, the lateral quadrupole is related to fluctuating shear forces. A longitudinal quadrupole is where the force vectors are parallel to each other but in line. As suggested in the figure, the longitudinal quadrupole is related to stretching forces (Poisson ratio type deformation).
Lateral Quadrupoles
[edit | edit source]These can be modeled as four monopoles, two dipoles, or two vortex rings. The force vectors for the dipoles are shown in the upper figure, the flow field for other two are shown in the figures on the right. There is no strictly radial flow vector that suggests effective sound generation. Although not shown, the radial component of the oblique flow at four forty- five degree angles is the maximum (See the above animation). Consequently there are four sound lobes that can be deduced without recourse to mathematics. This type of quadrupole can exist in flows that have a velocity gradient, and especially in turbulent flows.[23][24]
Modeling the Lateral Lateral Quadrupole Flow Field
[edit | edit source]The fluid mechanics of the close-in flow field of the lateral quadrupole can be modeled in several ways. The figure on the left used four monopoles to create the flow field. It is this arrangement that was the basis for the first equation in the next section. The center figure used two dipoles, pictured here as two spheres, to create the flow field. Two force vectors could also have been used. The right hand figure used two vortex rings to create the flow field. Distributions of lateral quadrupoles exist in flows with velocity gradients, and especially high speed turbulent flows.



Lateral Quadrupole Theory
[edit | edit source]A lateral quadrupole is one where the force vectors are in parallel but alongside each other line as suggested by the upper figure on the upper right. As with the less complex sources, this quadrupole has been considered as a collection of four point monopoles, each pair separated by a finite distance d longitudinally and both pairs separated by a distance D laterally. The equation below is an expression for the sound pressure in these terms.[25] The source function Q here is that of a point monopole.
A more illuminating method would be to use the derivative method. As the dipole velocity potential was obtained as the derivative of the monopole, the lateral quadrupole velocity potential can be obtained by the derivative of the dipole potential. For the lateral quadrupole, the derivative is taken at right angles to the direction of the primary dipole axis. This method reveals the shear forces acting on the volume. The first equation is the velocity potential; the second is the sound pressure; the third is the mean square sound pressure. The lateral quadruple sound source can be expressed as the time average of the mean square of the time rate of change of the shear forces acting on the volume.
The directivity of this quadrupole is shown in the figure n the right. The three dimensional form is much like an elongated balloon.

where the time derivative represents the time varying stresses applied to the medium.
Scaling Lateral Quadrupole Sources
[edit | edit source]As was done with the monopoles and dipoles, geometric and dynamic similarity can be applied to quadrupoles by using a characteristic dimension L and a characteristic speed U. The first equation below, using simplified form of the fluctuating stress τ (dimension F/L), is for a point quadrupole at a discrete frequency. The stress term can be replaced by a dimensionless version, and the frequency term can be replaced by the Strouhal number. If these dimensionless values are inserted in the sound power equation, the lower equation results. This is the well known speed law attributed to Lighthill. Since the Strouhal number is raised to a high power, one must not be surprised if the overall speed dependence deviates from that law.
The radiation impedance has been calculated as [26]

The figure on the right shows these impedances graphically. It is clear that resistive radiation efficiency R at low frequencies is considerably worse than for monopoles and dipoles while reactive impedance X is many orders of magnitude larger. The flow at these frequencies is primarily incompressible. This suggests that quadrupole sound radiation is more efficient at high frequencies and high shear stresses (high speed flows).
Lateral Quadrupole-like Sources
[edit | edit source]Theoretical models have their axes in defined directions, so one would expect to be able to measure source directivity. Unfortunately, not many higher order sources have such fixed directivity. The initial interest in these sources was in the noise from jet engines that was determined to be of quadrupole nature.[27][28] The flow from a subsonic jet is highly turbulent, so the source orientations are more nearly random. Most sound is generated in the region downstream of the nozzle exit with high velocity gradients and high turbulence, giving rise to lateral quadrupoles. The characteristic dimension L and the characteristic speed U are spatially varying both laterally and longitudinally. Sound measurements agree well with the eighth power law shown above.
Longitudinal Quadrupoles
[edit | edit source]Again, these can be modeled as four monopoles, two dipoles, or two vortex rings. The force vectors for the dipoles are shown in the upper figure, the flow field for other two are shown in the figures on the right. In tis case, there are purely radial flow vectors that suggest effective sound generation on the axis of the flow.
Modeling Longitudinal Quadrupole Flow Fields
[edit | edit source]The fluid mechanics of the close-in flow field of the longitudinal quadrupole can be modeled in several ways. The figure on the left used four monopoles to create the flow field. It is this arrangement that was the basis for the first equation in the next section. The center figure used two dipoles, pictured here as two spheres, to create the flow field. Two force vectors could also have been used. The right hand figure used two vortex rings to create the flow field. These models suggest the stretching of the volume.


Longitudinal Quadrupole Theory
[edit | edit source]A longitudinal quadrupole is one where the force vectors are in parallel and in line as suggested by lower figure on the upper right. As with the less complex sources, this quadrupole has been considered as a collection of four point monopoles, each pair separated by a finite distance d longitudinally and both pairs separated by a distance D longitudinally. The equation below is an expression for the sound pressure in these terms.[29] The source function Q here is that of a point monopole.
A more illuminating method would be to use the derivative method. As the dipole velocity potential was obtained as the derivative of the monopole, the longitudinal quadrupole velocity potential can be obtained by the derivative of the dipole potential. For the longitudinal quadrupole, the derivative is taken in the same direction as the primary dipole axis. This method reveals the stretch forces acting on the volume. The first equation is the velocity potential; the second is the sound pressure; the third is the mean square sound pressure. The longitudinal quadruple sound source can be expressed as the time average of the mean square of the time rate of change of the stretch forces acting on the volume.
The directivity of this quadrupole is shown in the figure n the right. The three dimensional form is much like an elongated balloon.

where the time derivative represents the time varying stresses applied to the medium.
Scaling Longitudinal Quadrupoles
[edit | edit source]Similar to the lateral quadrupole, a characteristic dimension L and a characteristic speed U must be chosen. The sound power equation below uses a simplified expression of the fluctuating stress τ (dimension F/L) for a point longitudinal quadrupole at a discrete frequency. Again, the stress term can be replaced by a dimensionless version, and the frequency term is replaced by the Strouhal number. The lower equation is similar to that for the lateral quadrupole.
Longitudinal Quadrupole-like sources
[edit | edit source]One demonstration of a longitudinal quadrupole-like sound field is the tuning fork.[30] When struck, the two bars of the fork oscillate out of phase. They act similarly to the two-dipole model shown in a previous section. The similarity to a true quadrupole is in the directivity of the sound field. The difference is in the finite distance between the two tines which are truly dipole sources. As long as the wavelength is long enough, the separation distance is important only in the near acoustic field.
References
[edit | edit source]- ↑ Lighthill, M., "On sound Generated Aerodynamically. Part I: General Theory", Proc. Royal Soc. London, 1952
- ↑ http://jullio.pe.kr/fluent6.1/help/html/acoustics/node4.htm
- ↑ Dawkins, S. "Aguide to Aeroacoustics", Bibliobazaar, 2011
- ↑ Norton, M. Karczub, D. "Fundamentals of Noise and Vibration Analysis for Engineers" Cambridge University Press, 2003
- ↑ http://gizmodo.com/5977824/the-biggest-bomb-in-the-history-of-the-world
- ↑ Kinlser, L.E., Frey, A.R., "fundamentals of Acoustics, John wiley and sons, 1962
- ↑ Morse, P.M., Ingard, K.U. "Theoretical Acoustics", McGraw-Hill, 1968
- ↑ http://www.scientificamerican.com/article/aerodynamic-whistles/
- ↑ Lighthill, M., "On sound Generated Aerodynamically. Part I: General Theory", Proc. Royal Soc. London, 1952
- ↑ Bernhard, R.J., Sandberg, U., "Where Does It Come From?", National Cooperative Highway Research Program, Report 630
- ↑ http://ccrllc/files/Tools-for-Analyzing-Sound-Sources.pdf
- ↑ Powell, A. "Theory of Vortex Sound," Jo. Acoust. Soc. Am., 36, 177-194, 1964
- ↑ Powell, A. "Vortex Sound: An alternative derivation of Mohring's formulation" Jo. Acoust. Soc. Am., 97, 684-686, 1995a
- ↑ Powell, A. "Vortex Sound Theory: Direct proof of equivalence of "vortex force" and "vorticity alone" formulations, n" Jo. Acoust. Soc. Am., 97, 1534-1537, 1995b
- ↑ Howe, M.S. "Vortex Sound", Cambridge University Press, 2003
- ↑ Strouhal, V. "Ueber eine besondere Art der Tonerregung" (On an unusual sort of sound excitation), Annalen der Physik und Chemie, 3rd series, 5 (10) : 216–251, 1878
- ↑ Phillips, O.M., "The intensity of Aeolian tones" Jo., Fluid Mech., 1, 607-624, 1956
- ↑ Chanaud, R.C., Powell, A., "Some experiments concerning the hole and ring tone", Jo. Acoust. Soc. Am., 37, 5, 902-911, 1965
- ↑ Vonnegut, B. "The Vortex Whistle" Jo. Acoust. Soc. Amer. 26, 16-20, 1952
- ↑ Chanaud, R.C., "Experiments Concerning the Vortex Whistle", Jo. Acoust. Soc., Amer. 35, No. 7, 953-960, 1963
- ↑ Powell, A., "On the Edge Tone", Jo. Acoust. Soc. Amer., 33, No. 4, 395-409, 1961
- ↑ Hayden, R.E., Fox, H.L., Chanaud, R.C. "Some Factors Influencing Radiation from flow interaction with edges of finite Surfaces", NASA Cr-145073, 1976
- ↑ Russell, D.A., Titlow, J.P., Bemmen,Y, "Acoustic monopoles, dipoles and quadrupoles:an experiment revisited", Am. J. Phys. 57, 8, August 1999
- ↑ Dowling, A.P., ‘‘Steady-State Radiation From Sources,'’ Encyclopedia of Acoustics, . John Wiley and Sons, Chap. 9, 107–125, 1997.
- ↑ Russell, D.A., Titlow, J.P., Bemmen, Y, "Acoustic monopoles, dipoles and quadrupoles: An experiment revisited", Am. J. Phys. 57, 8, August 1999
- ↑ Powell, A. Class Notes, UCLA, 1961
- ↑ Lush, P.A., "Measurements of subsonic jet noise and comparison with theory", Jo. Fluid Mech. 46,3, 477-500, 1971
- ↑ Goldstein, M. E., "A generalized acoustic analogy", Jo. Fluid Mech. 488, 315-333, 2003
- ↑ Russell, D.A., Titlow, J.P., Bemmen, Y, "Acoustic monopoles, dipoles and quadrupoles: An experiment revisited", Am. J. Phys. 57, 8, August 1999
- ↑ Russell, D.A., "On the sound field radiated by a tuning fork" Am. J. Phys. 68 ~121, December 2000





![{\displaystyle c_{0}^{2}(\rho -{{\rho }_{0}})={\frac {{\partial }^{2}}{\partial {{x}_{i}}{{x}_{j}}}}\int \limits _{V}{\left[{{T}_{ij}}\right]}{\frac {{{d}^{3}}y}{4\pi r}}-{\frac {\partial }{\partial {{x}_{i}}}}\oint \limits _{S}{\left[\rho {{u}_{i}}{{u}_{j}}+p_{ij}^{'}\right]{\frac {d{{S}_{j}}(y)}{4\pi r}}}+{\frac {\partial }{\partial t}}\oint \limits _{S}{\left[\rho {{u}_{j}}\right]{\frac {d{{S}_{j}}(y)}{4\pi r}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b75483b43dfda630514a935e11f85e64fa8b441)








![{\displaystyle {\begin{aligned}&p\left(r,t\right)=\left[{\frac {1}{1+ika}}\right]\left({\frac {a}{r}}\right){{Z}_{0}}{{u}_{a}}{{e}^{i\left(\omega t-k\left(r-a\right)\right)}}\\&k={\frac {\omega }{{c}_{0}}}={\frac {2\pi f}{{c}_{0}}}={\frac {2\pi }{\lambda }}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73821e313ba5c6f749792edaad70ba69052dc31b)

![{\displaystyle W=2Au_{a}^{2}R\left[1+{\frac {\sin(2kh)}{2kh}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c61c0c7483b62e0510bab6db4a734796cba55657)
![{\displaystyle W=Au_{1}^{2}R\left[1+\left({\frac {u_{2}^{2}}{u_{1}^{2}}}\right)+{\frac {2{{u}_{2}}}{{u}_{1}}}{\frac {\sin(2kh)}{2kh}}\cos \delta \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c271455b9ec11dd922eafd6cb6b590bc26dba8cd)








![{\displaystyle \phi (r,\theta ,t)={\frac {3{{F}_{z}}}{4\pi k{{Z}_{0}}}}\left[{\frac {1+ikr}{{r}^{2}}}\right]\cos \theta {{e}^{i(\omega t-kr)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5433288c4aa534d458a1976b7981e26f515abce)


![{\displaystyle {\begin{aligned}&{{I}_{r}}(r,\theta )={\frac {9F_{z}^{2}}{16{{\pi }^{2}}{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{r}^{2}}}{{{r}^{4}}(1+{{k}^{2}}{{a}^{2}})}}=+i{\frac {2+{{k}^{2}}{{r}^{2}}}{{{r}^{4}}(1+{{k}^{2}}{{a}^{2}})kr}}\right]co{{s}^{2}}\theta \\&{{I}_{\theta }}(r,\theta )={\frac {i9F_{z}^{2}}{32{{\pi }^{2}}{{Z}_{0}}}}\left[{\frac {1+{{k}^{2}}{{r}^{2}}}{{{r}^{4}}(1+{{k}^{2}}{{a}^{2}})kr}}\right]sin2\theta \\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0842d36a36d888a65e0db69beb76a961c8af59b7)
![{\displaystyle W={\frac {3F_{z}^{2}}{4\pi {{a}^{2}}{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{a}^{2}}}{1+{{k}^{2}}{{a}^{2}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4d8a806d04578d204f18dca05da85cfdcead473)

![{\displaystyle p{{p}^{*}}={\frac {9F_{z}^{2}}{16{{\pi }^{2}}(1+{{k}^{2}}{{a}^{2}})}}\left[{\frac {(1+{{k}^{2}}r_{1}^{2})}{r_{1}^{4}}}{{\cos }^{2}}{{\alpha }_{1}}+{\frac {(1+{{k}^{2}}r_{2}^{2})}{r_{2}^{4}}}{{\cos }^{2}}{{\alpha }_{2}}+{\frac {2\cos {{\alpha }_{1}}\cos {{\alpha }_{2}}}{r_{1}^{2}r_{2}^{2}}}\left[(1+k{{r}_{1}}{{r}_{2}})\cos k({{r}_{2}}-{{r}_{1}})+k({{r}_{2}}-{{r}_{1}})\sin k({{r}_{2}}-{{r}_{1}})\right]\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ddacaf278928a5fe82cfdbe6dd75d4be89e84f21)




![{\displaystyle {\begin{aligned}&\varphi (r,\theta ,\psi ,t)={\frac {3F}{4\pi k{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]\cos \theta \sin \theta \cos \psi {{e}^{i(\omega t-kr)}}\\&p(r,\theta ,\psi ,t)={\frac {i3F}{4\pi }}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]\cos \theta \sin \theta \cos \psi {{e}^{i(\omega t-kr)}}\\&{\overline {{p}^{2}}}(r,\theta ,\psi )={\frac {9{\overline {{\left({\frac {\partial F}{\partial t}}\right)}^{2}}}}{16{{\pi }^{2}}}}\left[{\frac {4+{{k}^{4}}{{r}^{4}}}{{r}^{6}}}\right]{{\cos }^{2}}\theta {{\sin }^{2}}{{\cos }^{2}}\psi \\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb6ceed5f4392505cfd9188503024dd4c31890ef)



![{\displaystyle {\begin{aligned}&\varphi (r,\theta ,t)={\frac {3F}{4\pi k{{Z}_{0}}}}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]{{\cos }^{2}}\theta {{e}^{i(\omega t-kr)}}\\&p(r,\theta ,t)={\frac {i3F}{4\pi }}\left[{\frac {{{k}^{2}}{{r}^{2}}-2(1+ikr)}{{r}^{3}}}\right]{{\cos }^{2}}\theta {{e}^{i(\omega t-kr)}}\\&{\overline {{p}^{2}}}(r,\theta )={\frac {9{\overline {{\left({\frac {\partial F}{\partial t}}\right)}^{2}}}}{16{{\pi }^{2}}}}\left[{\frac {4+{{k}^{4}}{{r}^{4}}}{{r}^{6}}}\right]{{\cos }^{4}}\theta \\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d444c5c2ff5c9d89cf361f3e3a3bcce3f2d97d60)
