Adventist Youth Honors Answer Book/Recreation/Canoeing
| Canoeing | ||
|---|---|---|
| Recreation General Conference |
Skill Level 2 | 
|
| Year of Introduction: 1945 | ||
|
The Canoeing Honor is a component of the Aquatic Master Award . |
1. Have the Intermediate level of the Swimming Honor.
[edit | edit source]Instructions and tips for earning the Swimming - Intermediate honor can be found in the Recreation chapter.
2. Demonstrate, first alone and then with a companion, the proper method of
[edit | edit source]a. Entering and launching a canoe
[edit | edit source](1) From a beach
[edit | edit source]This is much easier to do if the paddler gives up the idea of having dry feet. Wear a pair of sandals and wade right in. But it can also be managed without getting the feet wet. Slide the canoe's bow into the water and let the current (if there is one) push that end downstream. Hang onto the other end of the canoe (the stern) so that it does not get away. If two people are to enter the canoe, have the sternman stand with one foot on either side of the stern, steadying it with the knees. Then have the bowman enter the canoe from the right, by reaching over the canoe, grasping the left gunwale with the left hand, then setting the left foot in the center of the canoe (over the keel). Then the bowman grasps the right gunwale with the right hand and slowly shift bodyweight to the left foot, lifting the right foot over the gunwale. The bowman then carefully walks to the bow while holding onto the gunwales, finally taking position either on the bow seat, or kneeling in front of it. The bowman can then place the tip of the paddle blade into the ground (under water) to steady the canoe and keep it from floating off while the sternman enters.
The procedure for entering the canoe alone is much the same, except that the canoe will not be steadied by a companion. Concentrate on balance, and always keep your weight as centered over the keel as possible.
(2) From a landing dock or pier.
[edit | edit source]It is far more difficult to enter a canoe from a dock or pier than from a beach. This is because the canoe will not sit on the bottom of the river or lake helping to steady it as people enter. Instead, paddlers must be very careful to keep their weight centered over the keel until firmly in position. Once the first person is in the boat, that person should assume a kneeling position with the knees spread as far apart as the canoe will allow. This will allow the person to easily and quickly shift his or her weight to either the left or the right to steady the canoe as the other paddler enters. The paddler should also grip the dock or pier firmly to keep the canoe from pushing away while the partner has one foot in the boat and the other on the dock.
b. Landing and leaving a canoe
[edit | edit source](1) On a beach
[edit | edit source]When landing on a beach, the bow usually drives into the bank first. The mistake most novices make at this point is to begin exiting the canoe while the stern is still upstream from the bow. Allow the current to push the stern past the bow so that the bow is facing upstream. This is what a river will want to do to the canoe anyhow, so it is better if you do it while you are still firmly seated. The bowman is usually the first to exit, by stepping over the gunwale onto shore (or into the water if that's not an issue). Once the bowman's weight is out of the canoe, the bow will rise and the canoe will likely not be in contact with the river bottom anymore. The wise sternman will take a few strokes to get the bow back onto the bank, and the helpful bowman will assist by pulling the canoe gently as well. Do NOT haul the canoe out of the water with the sternman still inside. This puts excessive strain on the keel and can easily damage the canoe.
(2) On a landing dock or pier.
[edit | edit source]As with entering a canoe, exiting into a pier is far more difficult that exiting onto a beach. Position the canoe alongside the pier and hold firmly onto it. Place both hands on the pier and gently shift your weight to them, trying to not push the boat away as you do so. Lift your weight onto the pier, turn around, and sit. Then swing the legs out of the boat.
3. Accompanied by examining counselor, demonstrate correctly the following strokes
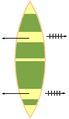
[edit | edit source]In the diagrams below, the bow is at the top and the stern is at the bottom. The hashed lines show the path of the paddle, with the hashes themselves indicating the orientation of the paddle's blade. The unhashed directional arrows show how the canoe will move when the stroke is executed.
-
Bow Stroke
-
Diagonal draw
-
Half sweep
-
J-Stroke
-
Reverse half sweep
-
Push-over stroke
-
Full sweep
-
Combination draw and J-stroke
a. Bow
[edit | edit source]The bow stroke is executed by inserting the paddle into the water well ahead of oneself with the blade perpendicular to the keel. The paddle is then pulled through the water parallel to the keel. This stroke is most often executed by the bowman, but can be used by the sternman as well.
b. Diagonal draw
[edit | edit source]The diagonal draw is a stroke used from the bow seat for gradual steering. It is made by inserting the paddle into the water well ahead and off to the side of the boat, then drawing the paddle towards the seat. A "regular" draw is similar, except that the paddle is inserted even with the seat instead of ahead.
c. Half sweep
[edit | edit source]A half sweep is used from either the bow or the stern to turn the canoe in the direction opposite to the paddle. In other words, if the paddle is on the left, the half sweep will turn the canoe to the left and vice versa.
When executing the half sweep from the bow position, the paddle is inserted into the water near the very front of the canoe with the power face of the paddle parallel to the keel. The paddle is then swept outward until it is straight out from the bow seat. The angle of power face is maintained perpendicular to the direction in which the paddle is drawn.
When executing the half sweep from the stern position, the paddle is inserted into the water straight out from the stern seat with the power face of the paddle perpendicular to the keel. The paddle is then swept around to the stern, and as when executed from the bow, the angle of power face is maintained perpendicular to the direction in which the paddle is drawn.
d. J-stroke
[edit | edit source]The J-stroke is so named because, when done on the port side, it resembles the letter J. It begins like a bow stroke, but towards the end the paddle is rotated and pushed away from the canoe with the power face of the paddle remaining the same throughout the stroke. This conveniently counteracts the natural tendency of the canoe to steer away from the side of the sternman's paddle.
e. Reverse half sweep
[edit | edit source]The reverse half sweep is a steering stroke executed from either the bow or the stern. It is executed in exactly the same fashion as the half sweep except in reverse.
f. Push over
[edit | edit source]The push over stroke is more often called a pry. This stroke is designed to move the canoe sideways. It is executed by inserting the paddle into the water with the power face pointing away from the keel. The center of the paddle is rested on the gunwale while the top of the paddle is pulled toward the center of the boat. As this is done, the blade should move away from the boat.
g. Full sweep
[edit | edit source]A full sweep is another steering stroke that can be executed from either the bow or the stern. In both instances, the paddle is inserted into the water well ahead of the paddler with the power face parallel to the keel. The paddle is then swept through a 180° arc.
h. Combination draw and J-stroke
[edit | edit source]The combination draw and J-stroke is exactly what it seems to be - a combination of a draw stroke followed by a J-stroke. This stroke is only executed from the stern and is used to gradually steer the canoe to the left if made on the left side of the canoe, or to the right if made from the right side of the canoe.
4. Alone and with a companion in both the bow and stern, paddle a canoe in a straight course for 100 yards (91.4 meters). Turn right about and left about. The paddle should be kept always on the same side of the canoe. Demonstrate two kneeling positions for paddling.
[edit | edit source]Paddling a straight course
[edit | edit source]The easiest way to paddle a straight course while keeping the paddle on the same side of the canoe is for the sternman to use the J-stroke. The bowman can paddle from either side of the canoe using bow strokes. When paddling solo, it is best to sit in the bow seat with the canoe turned around so that the stern (the back of the canoe) becomes the front. By doing this, the paddler will be positioned closer to the middle of the canoe, because the bow seat is closer to the center than the stern seat. Again, the J-stroke should be used.
Turning
[edit | edit source]If paddling on the right side of the canoe, the sternman can effect a left turn by applying simple bow strokes. The canoe will turn left. To turn right while paddling on the right side of the canoe, the sternman applies reverse bow strokes while the bowman applies draw strokes. Both turns can also be effected with forward and/or reverse sweeps.
Kneeling positions
[edit | edit source]Kneeling in a canoe gives it greater stability because it lowers the center of gravity. It also allows the paddler greater control over the canoe's side-to-side tilt because the weight can be quickly shifted to the left or to the right to counter tipping. When sitting, this is more difficult to do because shifting the weight from one buttock to the other does not have much effect.
The first kneeling position is to place both knees on the bottom of the canoe and rest the buttocks against the front edge of the seat. The second kneeling position is similar, except that only one knee is on the bottom - the other knee is raised and the foot is on the bottom of the boat (as if proposing marriage). The paddler may still lean against the front edge of the seat.
5. Demonstrate with a canoe the rescue of a companion who has capsized his canoe offshore by
[edit | edit source]a. Emptying the swamped canoe of water by drawing it upside down across the gunwales of the rescue canoe.
[edit | edit source]First maneuver the rescue canoe such that it is perpendicular to the swamped canoe, with either the bow or the stern of the swamped canoe near the center of the rescue canoe. Turn the swamped canoe upside down (if it is not in this position already). One rescuer may then reach over the gunwales, take hold of the bow or stern of the swamped canoe and lift it onto the gunwale. The other rescuer should counterbalance the rescue canoe while this is being done to prevent the rescue canoe from swamping as well. This is done by having the rescuer shift his or her weight to the opposite side of the rescue canoe.
Once the bow or stern is resting on the gunwales, the swimmers should help by pushing the swamped canoe up onto the gunwales of the rescue canoe (so that the gunwales of both canoes are in contact). The rescuers will also draw it across. When the swamped canoe is centered on the gunwales of the rescue canoe, one rescuer will roll the swamped canoe right-side-up. The other rescuer will catch it as it rolls around. The keel of the rescued canoe will then be sitting on the gunwales of the rescue boat, and can then be slid back into the water.
b. Launch the rescued canoe again.
[edit | edit source]The rescuers then gently shove the canoe off their gunwales back into the water. Be careful not to hit the swimmers.
c. Steady canoe while companion climbs aboard.
[edit | edit source]The canoe is then turned parallel to the rescue canoe, and both rescuers will hold the gunwales of the two canoes firmly together. The swimmers may then re-enter the canoe from the opposite side (it is best for them to do this one at a time).
6. Jump out of a canoe in deep water and get back in again in the proper form without shipping water. (Candidate must be accompanied by lifeguard in an equipped lifeboat.)
[edit | edit source]The least risky way to jump out of a canoe is by jumping off the deck (that is, jumping off the bow to the front of the canoe, or jumping off the stern to the rear).
The paddler should then swim to the center of the canoe and grab the gunwales with both hands. The hands should be positioned about a shoulder-width apart. The paddler then lifts himself up, throwing the torso across the gunwales and getting as much body weight over the keel as possible. If possible, one hand should reach across the canoe to the opposite gunwale during this motion. With the belt-line over the near gunwale, the paddler may then swing his legs aboard.
7. With clothes on
[edit | edit source]The Pathfinder should wear a swimsuit beneath an outer layer of clothing for this requirement.
a. Capsize a canoe in deep water.
[edit | edit source]This is surprisingly difficult in some canoes, but can be accomplished by leaning the canoe over as far as possible, then standing on the gunwale. As soon as the gunwale dips below the surface of the water, capsizing will quickly follow.
b. Right canoe and stow paddles and kneeling pad.
[edit | edit source]Swim alongside the canoe and lift the gunwale back above the surface. The canoe should not sink even when it's full of water.
c. Get in canoe filled with water and paddle with hands or paddle for 25 yards (22.9 meters).
[edit | edit source]This is done just as described previously, except that the canoe is almost certain to ship more water. Don't worry about it. Once you get inside, it is very possible that both gunwales will still be submerged below the surface. It is sometimes possible to get some of the water out by lifting the bow or stern as high as you can while the canoe is still upside-down. Then with a quick motion, throw the canoe higher with a twisting motion to right it.
d. Disrobe, stow clothes and paddle, go overboard, hold on to bow of canoe with one hand, swim and tow swamped canoe to shore.
[edit | edit source]Removing wet clothing is more difficult than it seems it should be. It tends to cling to the body. If wearing a swimsuit under an outer layer, there is no need to remove the swimsuit as well. Choose loose clothing if possible. A shirt that buttons will be easier to get off than a pull-over. Jump back into the water, take hold of a rope tied to the bow (or a grab-loop), and swim until you are in shallow water.
e. Empty canoe properly and land it. (Candidate must be accompanied by a lifeguard in an equipped lifeboat.)
[edit | edit source]Once the canoe is in shallow water, turn it on its side and continue to haul it onto the beach. This will empty it of most water. If you attempt to haul it out of the water while it is still full, you will find that it is very heavy, and it may not even be possible for you to turn it over or move it. This is why it should be turned on its side or even upside-down. Once most of the water is out of the canoe, it is a simple matter to pull it onto shore.
8. Fully satisfy the examiner of a thorough knowledge of safety rules which will make the candidate a safe canoeist and competent to take others out in a canoe. Promise to observe these rules at all times.
[edit | edit source]- Wear a Personal Flotation Device (PFD) at all times.
- Do not drink alcohol while canoeing
- Paddle directly into or away from the wake made by power boats (broadside waves can easily capsize a canoe).
- If you capsize in still water, stay with the canoe.
- If you capsize in swift current, try to get upstream relative to the canoe so that it will not pin you on a rock. A canoe full of water easily weighs 1200 kg
 , and if it pins you against a rock, you are not going to lift a 1200 kg canoe off yourself. The only other available option is to drown, and that is not a very attractive option at all.
, and if it pins you against a rock, you are not going to lift a 1200 kg canoe off yourself. The only other available option is to drown, and that is not a very attractive option at all. - If you find yourself swimming in a rapid, roll onto your back and float with your feet going downstream first and your toes out of the water. This will prevent your foot from catching a rock and it getting trapped. Many people have drowned as a result of foot-entrapment.
- Kneel in the bottom of the canoe in rough water. This increases the boat's stability by lowering its center of gravity, and it gives you better control of the canoe.
- Do not paddle in water that presents a greater challenge than your abilities. Do not be too embarrassed to admit that a rapid is too difficult for you. You won't be able to admit it if you drown.
- Do not paddle farther from shore than you can swim.
- Load the canoe properly so that it is balanced from bow to stern and from side to side.
- Stay away from low-head dams. They may look innocuous, but they are very dangerous. Do not approach them from upstream or from downstream.
- Never paddle alone.
- Do not paddle into tree branches, especially if they are underwater. Water will pass right through, but if you fall out of the canoe, you will be pinned against them. Moving water is very powerful. You are puny in comparison. Water moving through a hydro-electric dam can generate enough electricity to power a city (including subway trains). If water is powerful enough to move a train, it is powerful enough to hold you under water pinned to a tree branch.
- Do not stand in a canoe until you have sufficient skill and experience to do so. Many people would argue that you should never stand in a canoe, but if you have sufficient skill, standing will allow a better view of the river ahead. This can be crucial above a rapid. That said, most people do not have sufficient skill. As the instructor of this honor, it's up to you to decide how to teach this "rule."
- Always use common sense. If something looks dangerous, it probably is.
- Always follow the 7 Leave No Trace Principles
- Plan ahead and prepare.
- Travel and camp on durable surfaces.
- Dispose of waste properly.
- Leave what you find.
- Minimize campfire impacts (be careful with fire).
- Respect wildlife.
- Be considerate of other visitors.
9. Explain how to do the following emergency repair work
[edit | edit source]For both of these situations, duct tape is the paddler's best friend.
a. Repairing a one-inch hole in fiberglass, canvas, and aluminum canoe.
[edit | edit source]Land the canoe on a beach, get it in the sun, flip it upside down. Dry the affected area as best you can with whatever you have. Let the sun do the rest. Apply a strip of duct tape to the outside of the hull, covering the hole completely. Then turn the boat right-side-up again, dry the inside of the hull around the hole, and cover it with duct tape as well.
b. Repairing a broken paddle shaft.
[edit | edit source]Find a straight tree branch about 2.5 cm![]() in diameter and 60 cm
in diameter and 60 cm![]() long. Join the two halves of the paddle together as best you can, then position the tree branch along side it. Wrap the paddle shaft and the branch with several turns of duct tape, both above and below the break. Paddle gently.
long. Join the two halves of the paddle together as best you can, then position the tree branch along side it. Wrap the paddle shaft and the branch with several turns of duct tape, both above and below the break. Paddle gently.
Once back from your trip, a more permanent repair can be made. Sand your paddle down right to the wood above and below the break. Drill 5cm![]() straight up into the center of the paddle shaft in both directions of the break. Cut the head off of a bolt the same diameter as your hole. Use a good quality marine epoxy to glue a 4" bolt in place in that hole. Wrap fiberglass cloth around the break and epoxy it in place. Now sand down the entire paddle and varnish. You will now have a strong lasting repair on your paddle. If the break was over where you grip the paddle, you may want to consider wrapping a thin twine around the shaft to make the grip even more comfortable, this process is called frapping or serving.
straight up into the center of the paddle shaft in both directions of the break. Cut the head off of a bolt the same diameter as your hole. Use a good quality marine epoxy to glue a 4" bolt in place in that hole. Wrap fiberglass cloth around the break and epoxy it in place. Now sand down the entire paddle and varnish. You will now have a strong lasting repair on your paddle. If the break was over where you grip the paddle, you may want to consider wrapping a thin twine around the shaft to make the grip even more comfortable, this process is called frapping or serving.
References
[edit | edit source]- Book:Adventist Youth Honors Answer Book/Honors
- Book:Adventist Youth Honors Answer Book
- Book:Adventist Youth Honors Answer Book/Skill Level 2
- Book:Adventist Youth Honors Answer Book/Honors Introduced in 1945
- Book:Adventist Youth Honors Answer Book/Recreation
- Book:Adventist Youth Honors Answer Book/General Conference
- Book:Adventist Youth Honors Answer Book/Aquatic Master Award
- Book:Adventist Youth Honors Answer Book/Completed Honors