A-level Physics (Advancing Physics)/Damping
Previously, our mathematical models of simple harmonic motion have assumed that the energy stored by a simple harmonic oscillator is constant. In reality, of course, resistive forces slow an oscillator down, transferring its energy to its surroundings. A pendulum will lose energy by moving the air. In addition to this, the motion of a mass on a spring will cause the spring to heat up, 'losing' the energy. This process is known as damping.
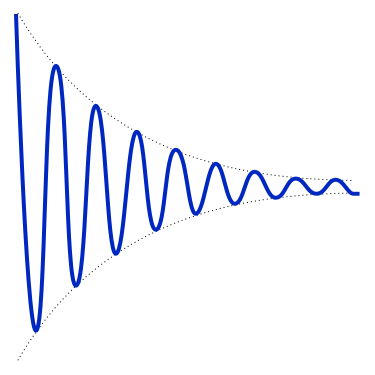
The principal effect of damping is to reduce the amplitude of an oscillation, not to change its frequency. So, the graph of the amplitude of a normal damped oscillation might look like the following:
Critical Damping
[edit | edit source]Critical damping occurs when a system is designed to return an oscillator to its equilibrium position in the least time possible. A critically damped oscillator, when damped, ceases to oscillate, and returns to its equilibrium position, where it stops moving. An example is the door closer. Normally, the door would swing back and forth, being damped by friction in the hinges, and air resistance. The door closer forces the door to stop swinging, and shut immediately. When closed, the door is in its equilibrium position.
Questions
[edit | edit source]1. Draw a graph of displacement for a critically damped oscillation.
2. How would you critically damp an oscillating pendulum?
3. How would you damp an oscillating pendulum using only a weighted polystyrene block?
4. What would the displacement graph look like for this oscillation, before and after damping began?
5. The graph above is an exponentially damped oscillation. If the displacement of the undamped oscillation is given by sin ωt, what is an approximate equation for the damped oscillation, in terms of a constant k which describes the degree to which the oscillation is damped?