A-level Mathematics/OCR/C2/Circles and Angles

Angular Measurement and Circular Sectors

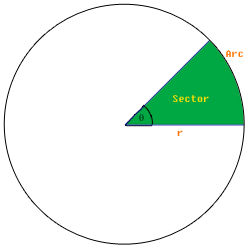
A section of a circle is known as a sector. One side of the sector is the radius. The portion of the circumference that is included in the sector is known as an arc.

Angular Degree

A circle has 360 degrees. Each degree can have 60 minutes (designated as ' ) and each minute can have 60 seconds (designated as " ). Since we can not convert minutes or seconds into radians directly we need to convert the minutes and seconds into a decimal number. Here is the formula:

Convert $X^{\circ }$ Y' Z" into degrees. $X+\left(Y\times {\frac {1}{60}}\right)+\left(Z\times {\frac {1}{3600}}\right)=X+{\frac {Y}{60}}+{\frac {Z}{3600}}$ For a practical example, convert $23^{\circ }$ 18' 38" into degrees. $23+{\frac {18}{60}}+{\frac {38}{3600}}=23.3106$

Angular Radian

A radian is the angle subtended at the centre of a circle by an arc of its circumference equal in length to the radius of the circle. Since we know that that the formula for the circumference of a circle is $C=2\pi r$ we can determine that there are $2\pi$ radians in a circle. We abbreviate radians as rad.

Conversion Between Degrees and Radians

Mathematics requires us to use radians for most angular measurements. Therefore we need to know how to convert from degrees to radians Since we know that there are $360^{\circ }$ degrees or $2\pi$ radians in a circle. We can determine these equations: $1^{\circ }={\frac {\pi }{180}}$

$1\ radian={\frac {180}{\pi }}$

So we can write these general formulae.

$X^{\circ }={\frac {X\times \pi }{180}}$

$X\ radian\left(s\right)={\frac {X\times 180}{\pi }}$

Here is an example convert $20^{\circ }$ into radians

$20^{\circ }={\frac {20\times \pi }{180}}={\frac {1}{9}}\pi \ rad$

Convert ${\frac {1}{9}}\pi$ into degrees.

${\frac {1}{9}}\pi \ radian\left(s\right)={\frac {{\frac {1}{9}}\pi \times 180}{\pi }}=20^{\circ }$

Arc Length

In most cases it is very difficult to measure the length of an arc with a ruler. Therefore we need to use a formula in order to determine the length of the arc. The formula that we use is:

$Arc\ Length=(\theta \ in\ radians)(radius)\,$ in symbols this is $s=\theta r\,$. Note: θ need to be in radians

Here is an example, determine the length of the arc created by a sector with a 6 cm radius and an angle of $53^{\circ }$.

The first thing we need to do is convert θ from degrees to radians.

$53^{\circ }={\frac {53\pi }{180}}rad$

Now we can calculate the length of the arc.

$s={\frac {53\pi }{180}}\times 6\approx 5.55cm$

Area of a Sector

The area of a sector can be found using this formula:

$Area={\frac {1}{2}}r^{2}\theta$Note: θ need to be in radians.

Calculate the area of a sector with a 3 cm radius and an angle of 2π.

$Area={\frac {1}{2}}3^{2}\times 2\pi \approx 28.3cm^{2}$

This is part of the C2 (Core Mathematics 2) module of the A-level Mathematics text.

Dividing and Factoring Polynomials / Sequences and Series / Logarithms and Exponentials / Circles and Angles / Integration

Appendix A: Formulae