A-level Computing 2009/CIE/Theory Fundamentals/Number representation
Binary:
- A denary value is a regular integer.
- A binary value is written as a collection of 1s and 0s.
- The first value in binary corresponds to a 1 in denary and the number to it’s left is double the previous number.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
- Using the table above we can calculate the denary value of the binary number. We can do this by adding the corresponding denary values of each column together.
- E.g. 2*1+16*1+64*1 = 82, so 01010010 is 82 in denary.
- Another way to memorize this is that each value is an increased power of 2.
Hexadecimal:
- Hexadecimal is a base-16 number system which means we will have 16 different characters to represent our value.
- After 9, values are represented by letters from A to F.
- Hexadecimal is written in the same way as binary, but instead of going up in powers of 2 we go up in powers of 16.
- E.g. F1 = 16*15 + 1*1 = 241
- A quick way to convert hexadecimal to binary is converting each individual value into and binary and putting them together.
- E.g. F = 0111 and 1 = 0001, therefore F1 in binary is 01110001.
Two’s Complement:
- We can represent a negative number in binary by making the most significant bit (MSB) a sign bit, which will tell us whether the number is positive or negative.
- If the MSB is 0 then the number is positive, if 1 then the number is negative.
|
Method: Converting a Negative Denary Number into Binary Twos Complement Let's say you want to convert -35 into Binary Twos Complement. First, find the binary equivalent of 35 (the positive version) 32 16 8 4 2 1 1 0 0 0 1 1 Now add an extra bit before the MSB, make it a zero, which gives you: 64 32 16 8 4 2 1 0 1 0 0 0 1 1 Now 'flip' all the bits: if it's a 0, make it a 1; if it's a 1, make it a 0: 64 32 16 8 4 2 1 1 0 1 1 1 0 0 This new bit represents -64 (minus 64). Now add 1: 64 32 16 8 4 2 1
1 0 1 1 1 0 0
+ 1
1 0 1 1 1 0 1
If we perform a quick binary -> denary conversion, we have: -64 + 16 + 8 + 4 + 1 = -64 + 29 = -35 |
|
Method 1: converting twos complement to denary To find the value of the negative number we must find and keep the right most 1 and all bits to its right, and then flip everything to its left. Here is an example: 1111 1011 note the number is negative 1111 1011 find the right most one 1111 1011 0000 0101 flip all the bits to its left We can now work out the value of this new number which is: 128 64 32 16 8 4 2 1
0 0 0 0 0 1 0 1
4 + 1 = −5 (remember the sign you worked out earlier!)
|
|
Method 2: converting twos complement to denary To find the value of the negative number we must take the MSB and apply a negative value to it. Then we can add all the heading values together 1111 1011 note the number is negative -128 64 32 16 8 4 2 1 1 1 1 1 1 0 1 1 -128 +64 +32 +16 +8 +2 +1 = -5 |
Image Representation:
- A bitmapped image is encoded by assigning a solid color to each pixel.
- Pixel: the smallest possible addressable area defined by a solid color, represented as binary, in an image.
- Image resolution:number of pixels an image contains per inch/cm.
- Screen resolution:the number of pixels per row by the number of pixels per column.
- Color Depth:the number of bits used to represent the color of a single pixel. An image with n bits has 2^n colors per pixel.
- File Size = Number of Pixels * Colour Depth
- Vector graphics:images defined using mathematics and geometry. Allowing for scalability.
- Drawing list: a set of commands used to define a vector image.
Sound Representation:
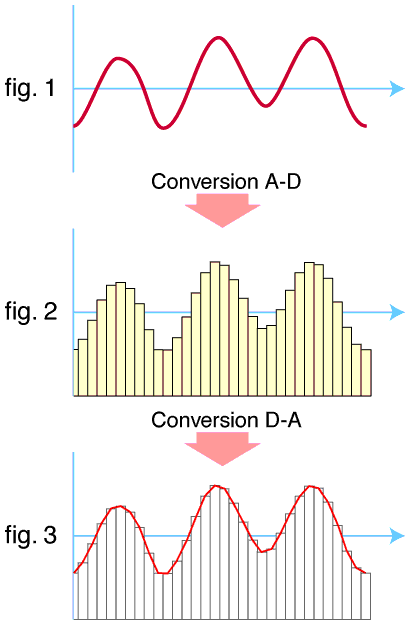
- Sound: vibrations that travel through a medium, they are are continuous in nature, which means there is infinite amount of detail for a sound.
- An analogue to digital converter(ADC) converts analogue sound into digital signals which can be digitally stored.
- A digital to analogue converter(DAC) converts digital signals into analogue sound that can be output.
- To convert a continuous wave signal into a digital form, the computer has to sample the sound.