Programming Concepts: Insertion Sort
| Class | sorting algorithm |
|---|---|
| Data structure | Array |
| Worst case performance | О(n2) |
| Best case performance | O(n) |
| Average case performance | О(n2) |
| Worst case space complexity | О(n) total, O(1) auxiliary |
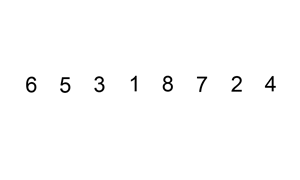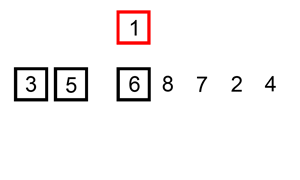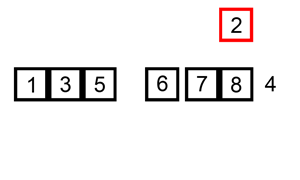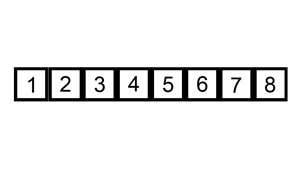
You should have covered bubble sort during the AS course. Unfortunately bubble sort is a very slow way of sorting data and very rarely used in industry. We'll now look at a much faster algorithm, insertion sort.
Insertion sort is a simple sorting algorithm: a comparison sort in which the sorted array (or list) is built one entry at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort and you may cover these at university. However, insertion sort provides several advantages:
- simple implementation
- efficient on small data sets
- uses a fixed amount of memory when running
Insertion sort requires the use of two arrays, one ordered, and one unordered. Each repetition of the algorithm moves an item from the unordered list, into a sorted position in the ordered list, until there are no elements left in the unordered list.
Sorting is typically done in-place without needing extra memory. The resulting array after k iterations has the property where the first k + 1 entries are sorted. In each iteration the first remaining entry of the input is removed, inserted into the result at the correct position, thus extending the result:
becomes
with each element greater than x copied to the right as it is compared against x.
|
Example: Insertion Sort The following table shows the steps for sorting the sequence {5, 7, 0, 3, 4, 2, 6, 1}. For each iteration, the number of positions the inserted element has moved is shown in parentheses. Altogether this amounts to 17 steps. 5 7 0 3 4 2 6 1 (0)
0 5 7 3 4 2 6 1 (2) 0 3 5 7 4 2 6 1 (2) 0 3 4 5 7 2 6 1 (2) 0 2 3 4 5 7 6 1 (4) 0 2 3 4 5 6 7 1 (1) 0 1 2 3 4 5 6 7 (6) for i ← 1 to i ← length(A)-1
{
// A[ i ] is added in the sorted sequence A[0, .. i-1]
// save A[i] to make a hole at index iHole
item ← A[i]
iHole ← i
// keep moving the hole to next smaller index until A[iHole - 1] is <= item
while iHole > 0 and A[iHole - 1] > item
{
// move hole to next smaller index
A[iHole] ← A[iHole - 1]
iHole ← iHole - 1
}
// put item in the hole
A[iHole] ← item
}
' a procedure to sort an array of integers
|
|
Exercise: Insertion Sort Describe the process of insertion sort Answer:
Insertion sort is a simple sorting algorithm: a comparison sort in which the sorted array (or list) is built one entry at a time.
Show the how insert sort would work on the following unordered array: 9 6 7 1 2 Answer: sort left hand side is underlined 9 6 7 1 2 6 9 7 1 2 6 7 9 1 2 1 6 7 9 2 1 2 6 7 9 Show how the insert sort would work on the following unordered array G K L A J Answer: sort left hand side is underlined G K L A J G K L A J G K L A J A G K L J A G J K L Complete the trace table for the following code: Answer: |

