Problem Solving: Searching and sorting
Bubble Sort
[edit | edit source]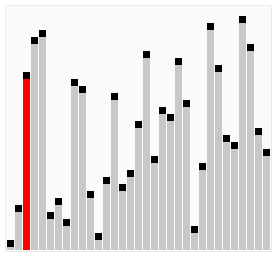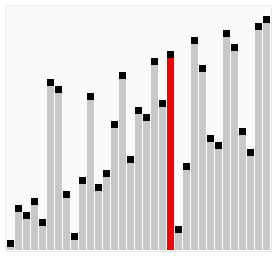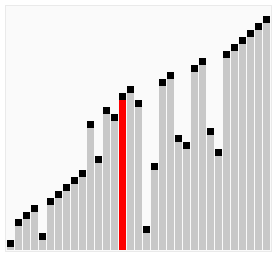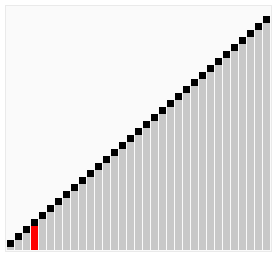
Bubble sort is a simple sorting algorithm that works by repeatedly stepping through the list to be sorted, comparing each pair and swapping them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which indicates that the list is sorted. The algorithm gets its name from the way larger elements "bubble" to the top of the list. It is a very slow way of sorting data and rarely used in industry. There are much faster sorting algorithms out there such as insertion sort and quick sort which you will meet in A2.

Step-by-step example
[edit | edit source]Let us take the array of numbers "5 1 4 2 8", and sort the array from lowest number to greatest number using bubble sort algorithm. In each step, elements written in bold are being compared.
First Pass:
( 5 1 4 2 8 ) ( 1 5 4 2 8 ), Here, algorithm compares the first two elements, and swaps them since 5 > 1
( 1 5 4 2 8 ) ( 1 4 5 2 8 ), It then compares the second and third items and swaps them since 5 > 4
( 1 4 5 2 8 ) ( 1 4 2 5 8 ), Swap since 5 > 2
( 1 4 2 5 8 ) ( 1 4 2 5 8 ), Now, since these elements are already in order (8 > 5), algorithm does not swap them.
The algorithm has reached the end of the list of numbers and the largest number, 8, has bubbled to the top. It now starts again.
Second Pass:
( 1 4 2 5 8 ) ( 1 4 2 5 8 ), no swap needed
( 1 4 2 5 8 ) ( 1 2 4 5 8 ), Swap since 4 > 2
( 1 2 4 5 8 ) ( 1 2 4 5 8 ), no swap needed
( 1 2 4 5 8 ) ( 1 2 4 5 8 ), no swap needed
Now, the array is already sorted, but our algorithm does not know if it is completed. The algorithm needs one whole pass without any swap to know it is sorted.
Third Pass:
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
( 1 2 4 5 8 ) ( 1 2 4 5 8 )
Finally, the array is sorted, and the algorithm can terminate.
Pseudocode implementation
[edit | edit source]The algorithm can be expressed as:
'''procedure''' bubbleSort( A ''':''' list of sortable items )
'''do'''
swapped = false
'''for each''' i '''in''' 1 '''to''' length(A) - 1 '''inclusive do:'''
'''if''' A[i-1] > A[i] '''then'''
swap( A[i-1], A[i] )
swapped = true
'''end if'''
'''end for'''
'''while''' swapped
'''end procedure'''
|
Exercise: Bubble Sort We will now look at an example in Visual Basic using an array of people's heights. The following data set is being passed:
Sub bubbleSort(ByRef height() As integer)
Dim swapped As Boolean
Dim temp As integer
'sort the elements
Do
swapped = False
For Count = 1 To MaxSize - 1
If height(Count + 1) < height(Count) Then
temp = height(Count)
height(Count) = height(Count + 1)
height(Count + 1) = temp
swapped = True
End If
Next
Loop Until swapped = False
'Print out the elements
For Count = 1 To MaxSize
Console.WriteLine(Count & ": " & height(Count))
Next
End Sub
Construct a trace table for the above code:
Answer:
What does the above code output?
Answer: 1: 12 Show the following lists after one pass of bubble sort: Sort into alphabetical order: Henry, Cat, George, Mouse Answer: Cat, George, Henry, Mouse Sort into alphabetical order: G, C, N, A, P, CAnswer: C, G, A, N, C, P Sort into numerical order: 12, 56, 0, 23, 10Answer: 12, 0, 23, 10, 56 Show the following after 2 passes Sort into alphabetical order: Emu, Shrike, Gull, Badger Answer: Emu, Gull, Badger, Shrike (Pass 1) Emu, Badger, Gull, Shrike (Pass 2) Sort into numerical order: 99, 45, 32, 56, 12 Answer: 45, 32, 56, 12, 99 (Pass 1) 32, 45, 12, 56, 99 (Pass 2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Let's look at a more complicated example, an array of structures, TopScores. The following data set is being passed:
| TopScores | ||
|---|---|---|
| Name | Score | |
| 1 | Michael | 45 |
| 2 | Dave | 78 |
| 3 | Gerald | 23 |
| 4 | Colin | 75 |
Sub bubbleSort(ByRef TopScores() As TTopScore)
Dim swapped As Boolean
Dim temp As TTopScore
'sort the elements
Do
swapped = False
For Count = 1 To MaxSize - 1
If TopScores(Count + 1).Score > TopScores(Count).Score Then
temp.Name = TopScores(Count).Name
temp.Score = TopScores(Count).Score
TopScores(Count).Score = TopScores(Count + 1).Score
TopScores(Count).Name = TopScores(Count + 1).Name
TopScores(Count + 1).Name = temp.Name
TopScores(Count + 1).Score = temp.Score
swapped = True
End If
Next
Loop Until swapped = False
'Print out the elements
For Count = 1 To MaxSize
Console.WriteLine(Count & ": " & TopScores(Count).Name & " " & TopScores(Count).Score)
Next
End Sub
|
Exercise: Bubble Sort (Harder) Draw a trace table to see if it works:
Answer:
The output should be: 1: Dave 78 2: Colin 75 3: Michael 45 4: Gerald 23 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Linear Search
[edit | edit source]The following pseudo code describes a typical variant of linear search, where the result of the search is supposed to be either the location of the list item where the desired value was found; or an invalid location -1, to indicate that the desired element does not occur in the list.
For each item in the list:
if that item has the desired value,
stop the search and return the item's location.
Return ''-1''
dim items() = {"h","g","a","d","w","n","o","q","l","b","c"}
dim searchItem as string
console.write("What are you searching for: ")
searchItem = console.readline()
For x = 0 to 10
If items(x) = searchItem Then
console.writeline("Found item " & searchItem & " at position " & x)
Exit For
End If
If x = 10 Then
console.writeline(-1)
End If
Next
Try the code above searching for items "w" and then for item "z":
|
Exercise: Linear Search "Cat","Mouse","Frog","Lion","Panda","Llama","Bee" For the array above, how many searches would it take to find the following data: "Panda" Answer: 5 "Camel" Answer: 7 and still it wouldn't find it! For an length list of items, what is the maximum number of searches it would take to see if an item is there or not? Answer: . This is seen as very slow, there is a faster ways of searching called binary search that you will learn about in A2, however, the data must be ordered first.
Make a trace table for the code above, where Answer:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Extension: Binary Search Linear search isn't very fast, for example if you had 1,000,000,000 names in a database and you searched for "Miles", four things might happen:
Or
The worst case scenario is 1,000,000,000 searches. The average case 500,000,000. There must be a faster way. There is! If your data is sorted then you can perform a Binary Search. This involves splitting the data into half. For example, let's search for Miles again in a much smaller list:
This only took 3 comparisons using binary search, it would have taken 7 using linear search. It gets even better when we use large lists. For example, our 1,000,000,000 item list would only take a maximum of 30 searches using Binary Search! It's very useful to have sorted data. You will learn more about binary search and the speed of algorithms in A2 |


