A-level Computing/WJEC (Eduqas)/Component 1/Data structures

Data structures are groups of related data items, organising data related to a real world problem. They consist of 1, 2 or 3 dimensional arrays which store data based on an index, records based around representative fields, stacks/queues which hold data based on when it was added, binary trees which contain nodes of data, lists holding data with pointers and hash tables holding data in a storage table.

There are 2 types of data structures, static and dynamic. Static data structures have a pre-defined size declared at the start of the program, which cannot be changed while the program is running. The advantage to a static structure is that the memory (RAM) requirements will be known. Dynamic data structures can expand and contract as the program runs. The necessary data can be added in, provided there is enough space in memory. The only issue with dynamic data structures is that they're much harder to implement.

Each data structure is useful for a different purpose. The efficiency is measured based upon how long the data takes to search through as the number of elements is increased. This is shown via Big o Notation.

Types of Data Structures

Arrays

1D

Set employees(5) As String = ["Alice", "Bob", "Cameron", "Courtney", "Daniel", "Emilia" ]

An array is a static set of elements of the same datatype, stored in a linear fashion. Each element is accessed by its index, with the first element having an index of 0 and each subsequent element being iterated by 1. To access the data in the array you specify the name of your array and which element you want to access, for example employees(0) to get the data for the first element.

0	1	2	3	4	5
Alice	Bob	Cameron	Courtney	Daniel	Emilia

2D

Set employees(5, 1) = [ ["Alice", "Bob" "Cameron", "Courtney", "Daniel", "Emilia"], [ 20, 38, 23, 50, 40, 35 ] ]

2-Dimensional (2D) arrays can be thought of as tables or just simply multiple 1-Dimensional (1D) arrays. To access an element in a 2D array you must specify the index of the column you wish to access and the index of the row you wish to access. This is formatted as (row, column). To declare a 2D array, two square brackets are used (one to indicate the start of a 2D array and the other to indicate the start of an element).

	0	1	2	3	4	5
Name [0]	Alice	Bob	Cameron	Courtney	Daniel	Emilia
Wage [1]	20	38	23	50	40	35

3D

Set employees(2, 1, 5) As String =

[

// Sales for the month of January.

[ ["Alice", 950] , ["Bob", 750], ["Cameron", 900], ["Courtney", 2500], ["Daniel", 2400], ["Emilia", 1500]  ],

// Sales for the month of February.

[ ["Alice", 1000] , ["Bob", 700], ["Cameron", 800], ["Courtney", 3000], ["Daniel", 2500], ["Emilia", 1700]  ]

]

3-Dimensional (3D) arrays are multiple 2D arrays grouped together or a collection of tables. Provided we have the table number, the column and the row, the data can be accessed (table number, row, column).

Sales for January 2018

	0	1	2	3	4	5
Name [0]	Alice	Bob	Cameron	Courtney	Daniel	Emilia
Sales [1]	950	750	900	2500	2400	1500

Sales for February 2018

	0	1	2	3	4	5
Name [0]	Alice	Bob	Cameron	Courtney	Daniel	Emilia
Sales [1]	1000	700	800	3000	2500	1700

Records

A record is a set of data items all related to a single individual or entity. Unlike an array, a record can contain data of different types. An example of a record is shown below.

Customers Record

	0	1	2
Name (string)	Alice	Bob	Daniel
Initial (character)	A	B	D
Age (integer)	24	34	18
Date of Birth (date)	08/04/1994	23/10/1984	09/12/2000

Stacks and Queues

A pile of pancakes is the same as a stack - it's a LIFO structure.

A stack is a LIFO data structure: Last In, First Out. This means data is removed in the opposite order to which it was added, with the most recent entry being the first to go. Think of it like a pile of pancakes - the top one has to be eaten before you can access any other pancakes underneath it. An example of a stack is the 'Undo' feature; the last thing you write is the first to be removed. A stack can be implemented simply by using an array; just use a pointer for the topmost item. Adding data to a stack is known as pushing, whilst removing data is called popping.

A queue, on the other hand, is a First In, First Out (FIFO) data structure. Data is removed in the order it was added, much like a conventional queue. Queues are used in printers to ensure jobs are printed in the order they arrive, and as a keyboard buffer to ensure each key is processed in sequence. Implementing a queue can also be done using an array, but this requires both a pointer for the top entry, and for the bottom, making it much more difficult to do effectively. The two methods used in a queue are 'enqueue' and 'dequeue'.

The pseudocode for popping (removing) and pushing (adding) an item is as follows:

Def pop(topItem):
If Stack(topItem) = NULL Then
    Output "Stack is empty - cannot pop."
    Return NULL
Else
    Value = Stack(topItem)
    Stack(topItem) = NULL
    topItem = topItem - 1   //  We must point to the previous item in the stack.
    Return Value
End If


Def Push(Value, TopItem):
If Stack Is Full Then
    Output "Stack is full - cannot push."
Else
    TopItem = TopItem + 1
    Stack(TopItem) = Value
    Output "Item added to the stack."
End If

You should also know the pseudocode for both the enqueuing and dequeuing methods:

Def Enqueue(Data)
If Queue Is Full Then

   Output "Queue is full - cannot enqueue."

Else

   TopItem = TopItem + 1
   Queue(TopItem) = Data
   Return TRUE

End If


Def Dequeue
If Queue Is Empty Then

   Output "Queue is empty - cannot dequeue."

Else

   Data = Queue(BottomItem)
   BottomItem = BottomItem + 1
   Return TRUE

End If

Linked Lists

A linked list is a set of data elements, where each element contains the data itself and pointer to the next element. The final element has a pointer to a rogue value (NULL), signifying the end of the list. The advantages of using a linked list are that new items can be inserted into a linked list without rearranging all the other elements. Linked lists can be implemented using a 2D table where the first entry of each row would contain the data, whilst the second entry would be the pointer, containing the row index for the next data point. To remove data from a linked list you adjust the node before it to point to the item after it, bypassing the link, but preserving the order of items.

• 
  This is a linked list with pointers and a rogue value "null".

Binary (Search) Trees

A binary search tree is composed of nodes and the links between them. Each node has up to two more coming off it, similar in design to a family tree or a factor tree. The most important aspect of a binary search tree, is that the data on the left branch must be less than the data in the root node, and the data on the right branch must be more than the data held in the root node. A binary tree is said to be balanced if nodes are evenly distributed across the tree, giving a minimum height. An unbalanced tree has many more nodes on one side than the other.

This is an approximately balanced binary tree, with the root node "8"

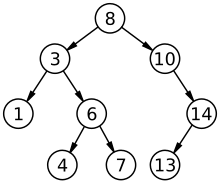
There are 3 main ways to navigate a binary search tree. These are:

• Pre-Order Traversal (NLR) - Starts at the root node, traverses the left sub-tree, then the right. This would give 8, 3, 1, 6, 4, 7, 10, 14, 13
• In-Order Traversal (LNR) - Traverses the left sub-tree, visits the root node, then traverses the right sub-tree. This would give 1, 3, 4, 6, 7, 8, 10, 13, 14
• Post-Order Traversal (LRN) - Traverses the left sub-tree, then the right, before visiting the root node. This would give 1, 4, 7, 6, 3, 13, 14, 10, 8

To add data to a binary search tree, begin by comparing the new entry to the current node. If the new data is greater, follow the right pointer, otherwise follow the left. Repeat this process until there is no pointer to follow for the correct direction. Create a new pointer here, in the direction given by the comparison and insert the new data at the end. If you are asked to draw a binary search tree given a list of data, follow this procedure for each data piece in order.

You could be asked to represent a binary tree using a 2D array (table). Each element will have a numerical ID from left to right (8 would be 1, 3 would be 2, 10 would be 3,etc.) This can be done in a similar way to a linked list, with each row containing the data, the left pointer and the right pointer (using NULL if there is no pointer).

ID	Left Pointer	Data	Right Pointer
1	2	8	3
2	4	3	5
3	NULL	10	6
4	NULL	1	NULL
5	7	6	8
6	9	14	NULL
7	NULL	4	NULL
8	NULL	7	NULL
9	NULL	13	NULL

Hash Tables

A hash table is a special type of data structure, where qualities of the data are used to decide where the data is to be stored. A hash table has two main parts - a hashing function and a storage table.

The hashing function plays the key role for a hash table. It is a secret function, known only to the developers, that decides where data should be stored, is based on replicable calculations that are derived from properties of the data itself. Hashing functions are usually very complex, but a simple example could be length(data) MOD 11. This would find the number of characters in a data entry, then find the remainder when dividing that value by 11. The number returned can then be used as an index in the storage table.

Array Before Data Input

0	1	2	3	4	5	6	7	8	9	10

Start Data	Hashing Function Operation	End Array Position
54	54 MOD 11	10
26	26 MOD 11	4
93	93 MOD 11	5
17	17 MOD 11	6
77	77 MOD 11	0
31	31 MOD 11	9

Array After Data Input

0	1	2	3	4	5	6	7	8	9	10
77				26	93	17			31	54

The problems with using a hash table also arise from the hashing function. It is important to use a hashing function that spreads data evenly in a table, and preferably over a wide range, to avoid two different data pieces being written to the same index. This is, however, impractical, especially if the hashing algorithm only has a limited number of outputs. A more practical solution is to have a new data structure at each index to allow multiple entries to be stored under there. This could be a linked list, or maybe even a new hashing table with it's own hashing function, but this will also increase the time taken for data storage and retrieval.