Basics of functional programming

Function - a rule that assigns a specific output for every given input

Domain - the set of data that comprises the inputs of a function

Co-domain - the set of data from which the outputs of a function are chosen

A function is a rule that connects a set of inputs to given outputs. We can model the inputs as SetA, with the outputs being chosen from the SetB. It is not necessary that every member of SetB will be mapped to an input from SetA. In the example below, SetA describes the inputs as being the Natural numbers (positive integers and zero, ${N}$), the function is the doubling of the inputs. The outputs are from SetB, the set of Natural numbers, note that not all elements of SetB are mapped from SetA, e.g. no doubling of a positive integer will ever map to the number 3.

Another name for the set that describes the inputs is the domain, the set from which the possible outputs are chosen is called the co-domain. The type of the domain and the co-domain do not have to be the same. For example we could have a function that told us whether a given positive integer input was a prime number. In this case the domain would be Natural numbers (${N}$), and the co-domain the boolean values True and False, as shown below:

Another way of explaining the working of functions is by describing the function type. The rule of the doubling function above can be written as f: A → B, this describes function f being a rule that maps the argument (input) type A to result (output) type B. Replacing A and B with their datatypes and f with a name gives us:

doubleNumber: integer -> integer

We can also write the isPrime function as a function type:

isPrime: integer -> boolean

Other examples of function types include:

isCorrectPassword: string -> boolean

MD5HashingAlgorithm: string -> string

phoneNumberSearch: string -> integer

First-class objects

In a functional programming language functions are first-class objects. This means that they can be used in the following ways:

• be assigned to a variable
• be assigned as arguments
• be returned in function calls
• appear in expressions

Let's see this in action (you will learn more about what this code codes as you follow this chapter),

.> byThePowerOf x y = x^y -- assigning to a variable
.> 3 * byThePowerOf 2 2   -- appearing in an expression
12
.> superPower x y = x^y
.> superPower 2 (byThePowerOf 2 2) -- assigned as an argument
16
.> twoToSomething = superPower 2 -- returned by a function call
.> twoToSomething 4
16

You will have already used first-class objects when writing procedural programming code where integers, characters and other datatypes, along with variables are used as arguments, returned by function calls, appear in expressions and can be assigned to variables.

Haskell declarations

In Haskell when you want to declare a value and attach it to a name you can use the = command like most other languages:

.> years = 17
.> seconds = years * 365 * 24 * 60 * 60
.> name <- getLine
Kim
.> print("Hey " ++ name ++ ", you are " ++ show seconds ++ " seconds old")
"Hey Kim, you are 536112000 seconds old"

If we wanted to declare our own version of pi, we could write:

.> myPi = 3.14
.> myPi * 3
9.42

But, as you hopefully remember, variables in functional programming are immutable, and we shouldn't be able to edit the value of myPi once we have declared it in a program:

varyingTrouble.hs
myPi = 3.14 myPi = 4

Attempting to compile this code from the command line gives an error, Haskell won't let you declare the same thing twice. In other words it won't let you change the value of something once it has been declared, variables in Haskell are immutable:

.> :l varyingTrouble.hs
main.hs:2:1: error:
    Multiple declarations of ‘myPi’
    Declared at: varyingTrouble.hs:1:1
                 varyingTrouble.hs:2:1
  |
2 | myPi = 4
  | ^^^^

Extension: Let and Where This chapter gives a very simple introduction to Haskell declarations that resembles the construction of a variable or constant in other languages. The let and where commands offer better functionality, learn more about them over at learn you a haskell.

Exercise: Functional programming foundations Describe the domain and the co-domain Answer: domain - the set of values from which a function's inputs are taken. co-domain - the set of values from which a functions outputs are chosen. Not all co-domain values need to be outputs. Which is these statements is true the type of the domain and the co-domain is always the same the co-domain is always smaller than the domain every value in the domain has a unique matching value in co-domain the output of a function doesn't always have to match every value of the co-domain Answer: 4. Write the function type description for a function that take a person's postcode as an argument and returns the the crime statistic for the area as a number between 1 and 5. Answer: postCodeCrime: string -> integer Write the function type description for a function that takes the year as a number and tells you whether it is a leap year Answer: leapYear: Integer -> Boolean Write the function type for the following function: ConvertMonthNumbertoName Answer: ConvertMonthNumbertoName: integer -> string

Writing our own functions

Now that we have learnt how to write simple functional programs using Haskell's inbuilt functions we will start to define our own functions. To do this we write the name of the function along with any arguments it might take, then set the return value as a calculation or short piece of code. For example:

$\underbrace {byThePowerOf} _{\text{function name}}\underbrace {x\ y} _{\text{arguments}}=\underbrace {x^{\wedge }y} _{\text{calculations for output}}$

.> byThePowerOf x y = x^y
.>
.> byThePowerOf 2 3
8
.> isMagic x = if x == 3 then True else False
.>
.> isMagic 6
False
.> isMagic 6.5
False
.> isMagic 3
True

Haskell uses static typing, the type of every parameter and return value is known at compile time, unlike languages such as Python which are dynamically typed. When we write functions we can declare the types that should be used for the arguments and the output, meaning that we will have better control over how the compiler creates the functions we define.

There are several base types in Haskell (which are always written starting with a capital letter) including: Integer, Float, Double, Bool, Char

Let us create a function that tells us if a number is magic or not, where three is the magic number. Before we write the code of the function, we define the name of the function isMagic, along with the type of the input (Integer) and the type of the output (Bool). For this we will be writing the code in a separate text file.

definingDataTypes.hs
isMagic :: Integer -> Bool isMagic x = if x == 3 then True else False

This means that when we load this code it will only accept integer inputs, anything else will return an error. And we also know that it will return a boolean value if given an integer input.

.> :l definingDataTypes
[1 of 1] Compiling definingDataTypes    ( definingDataTypes.hs, interpreted )
Ok, one module loaded.
.> isMagic 3
True
.> isMagic 7
False
.> isMagic 7.5
<interactive>:5:9: error:
    • No instance for (Fractional Int) arising from the literal ‘7.5’
    • In the first argument of ‘isMagic’, namely ‘7.5’
      In the expression: isMagic 7.5
      In an equation for ‘it’: it = isMagic 7.5

Other Haskell examples of declaring the function type and the function code include:

function	example call
factorial :: Integer -> Integer factorial 0 = 1 factorial n = n * factorial (n - 1)	.> factorial 3 6

function	example call
abc :: Char -> String abc 'a' = "Apple" abc 'b' = "Boat" abc 'c' = "Cat"	.>abc 'c' "Cat"

function	example call
byThePowerOf :: Integer -> Integer -> Integer byThePowerOf x y = x^y	.> byThePowerOf 2 3 8

The output type is always the last datatype specified in in the -> list. All the other datatypes define the inputs. In the byThePowerOf example above there are three types listed Integer -> Integer -> Integer. The first two Integer data types specify the argument types and the last data type listed, the final Integer, specifies the output type.

Extension: Haskell type variable You can find out the type(s) of something in Haskell by using the :t command. For example: .> :t 234.5111111 234.5 :: Fractional p => p .> :t max max :: Ord a => a -> a -> a a is odd as it is a type that doesn't start with capital letter like the other date type names, it is a type variable. This means that the max function isn't bound to using any particular type, but by it having a three times it means that we have to pass the same variable type to both arguments of the max function, and the max function will return a value of the same type as the arguments. Find out more over at learn you a haskell

Exercise: Writing your own functions Write a function in Haskell along with the type definition to output the area of any circle given its radius Answer: circleArea :: Double -> Double circleArea r = 3.14 * r^2 -- alternatively circleArea r = pi * r^2 Write a function in Haskell along with the type definition to output the average of three numbers that have decimal points Answer: avgThree :: Double -> Double -> Double -> Double avgThree x y z = (x + y + z) / 3 Write a function in Haskell along with the type definition to output whether someone can see an 18+ movie when they give their age in years. Answer: letThemIn :: Integer -> Bool letThemIn y = if y >= 18 then True else False

Function application

Giving inputs as arguments to a function is called the function application. del(7,9) is the application of the function del (delete) to the arguments 7 and 9. This can be written as:

f: integer x integer -> integer

Which describes the function f being defined by the cartesian product of two integers, integer x integer; meaning any combination of both integer arguments can be accepted (x doesn't equal multiply). The final arrow (->) shows that the output of the function f on these integers is also an integer.

Whilst it looks like f accepts two arguments, because the argument is defined as a cartesian product, f only takes one argument, a pair of values, for example (7,9) or (101, 99).

Partial function application

Partial function - a function that has been called with only some of the required arguments, allowing it to be reused or used as a building block for other functions

Haskell might appear to have functions that take multiple arguments, e.g. max 2 2, but in reality a function in Haskell can only ever take one argument. How can this be? Looking at the example of the min function we can write the same function call in two different ways, both work:

.> min 50 13
13
.> (min 50) 13
13

The second example, (min 50) 13 is showing a partial function application. As you know through mathematics and previous programming, the inner brackets are always executed first. This means the (min 50) runs with only one input, when it needs two?! The code within the brackets return a function that is still waiting for the missing input before it can return a value, this is why we call it a partial function, (min 50) only partially runs. To make this clearer let's declare (min 50) as a variable:

.> LTL = min 50 -- assign a partial function as a variable
.> LTL 13       -- partial function LTL is completed by the argument 13
13              -- returning the result of (min 50) 13
.> LTL 8
8
.> LTL 90
50

Whilst the above example is rather trivial, you can see that instead of having to write min 50 multiple times, and all the mistypes that might entail, we can use the partial function LTL (Less Than L) instead.

We can describe the min function that we used above as the function type:

min: Integer -> Integer -> Integer

Passing a single Integer to min returned a function that took another Integer as an argument and returned an Integer. This can be written, with the brackets defining the return function, as:

min: Integer -> (Integer -> Integer)

Let's look at a more complex example that is trying to work out the volume of boxes. There are three Integer arguments x,y,z and one Integer output.

partialBoxes.hs
boxVol :: Integer -> Integer -> Integer -> Integer boxVol x y z = x * y * z

This can also be written as:

boxVol :: Integer -> (Integer -> (Integer -> Integer))

Let’s see how a partial function of boxVol can be used. By passing two arguments, 4 and 5, to boxVol at the same time we first create a partial function with 4 as the argument x, and Integer -> (Integer -> Integer) as the expected arguments and output. Haskell then passes 5 to this partial function, forming a new partial function. This is declared as standardBase. standardBase has x = 4 and y = 5 and it accepts Integer -> Integer as the expected argument and output. Passing 9 to the partial function standardBase then completes the function which can now return the value 180 (4 * 5 * 9).

.> :l partialBoxes.hs
[1 of 1] Compiling partialBoxes( definingDataTypes.hs, interpreted )
Ok, one module loaded.
.> standardBase = boxVol 4 5
.> standardBase 9
180
.> squareBase = boxVol 4 4
.> squareBase 9
144
.> standardBase 9
120

Demonstration of how partial functions are used to solve a multi argument function call

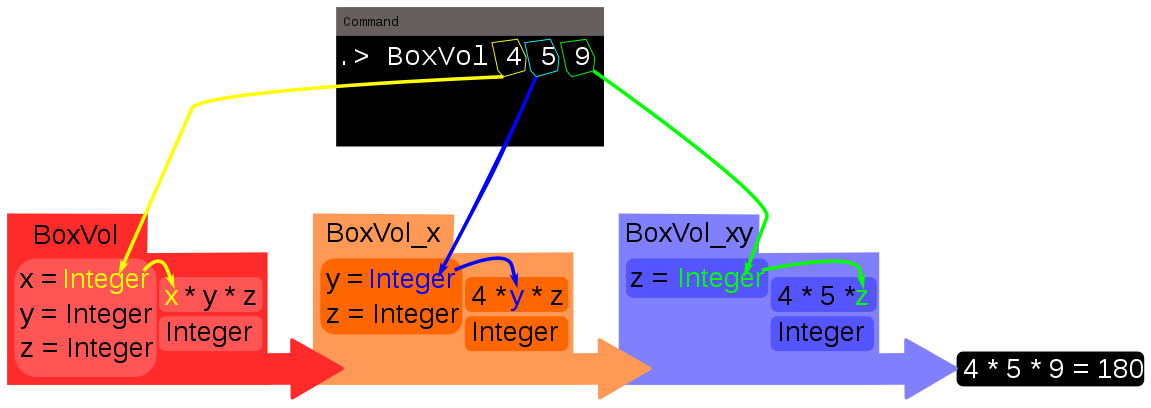
We create partial functions that have calculations involving one of more arguments already built into them. These partial functions are then ready to accept the other arguments to complete the function or make further partial functions. Partial functions can be used as the building blocks of other functions.

Function composition

Function composition - combination of two or more functions to create a new function

Sometimes you might want to combine two functions together, this is called function composition. Let's imagine that we have a function f of function type f: A -> B and another function g, of function type g: B -> C. We can use function composition to make a new function through the command g  ∘ f:

g  ∘ f: A -> C

For function composition to work, the co-domain of f must match the domain of g, e.g. f: A -> B = g: B -> C. Allowing the output of f to be mapped to the input of g. We can see this by looking at this example:

g(x) = x / 2

f(y) = y + 6

We know that the domain of g matches the codomain of f, and through g  ∘ f we take the input of g to be the output of f

input of g = x = f(y)

f(y) = y + 6

therefore x = y + 6

g(f(y)) = (y + 6) / 2

Another way of writing g  ∘ f is g(f(y)), which tells us that we should first calculate f, then map the output of f to the input of g.

We can perform function composition in Haskell by using the full stop symbol '.'. Taking the above example, we can turn this into code:

.> g x = x/2
.> f y = y + 6
.> (g.f) 3
4.5
.> h = g.f
.> h 5
5.5

To double check this is doing what we expect:

1. If y = 5,
2. then f(y) = 5 + 6 = 11,
3. mapping the output of f to the input of g through g  ∘ f gives x = 11,
4. calculating g gives 11 / 2 = 5.5.
5. Which is what we see above.

Exercise: Partial functions and function composition Why might we want to use partial functions? Answer: it allows us to build other functions out of pre-made blocks, or partial functions it makes mistyping of common statements less likely A carpet sales company wants to work out the volume of their carpets in store, they write the following code, what does it output? cylVol :: Double -> Double -> Double cylVol h r = (pi * r^2) * h fiveFooter = cylVol 5 sixFooter = cylVol 6 fiveFooter 4 sixFooter 4 Answer: 251.32742 301.5929 For the following functions, which of the numbered function compositions would be allowed? f: Integer -> Bool g: Integer -> Float h: Integer -> Integer i: Float -> Bool f ∘ g g ∘ h h ∘ f h ∘ h g ∘ g g ∘ i Answer: f ∘ g NO - domain of f is Integer, co-domain of g is Float g ∘ h YES - domain of g in Integer, co-domain of h is Integer h ∘ f NO - domain of h is Integer, co-domain of f is Bool h ∘ h YES - domain of h is Integer, co-domain of h is Integer g ∘ g NO - domain of g is Integer, co-domain of g is Float g ∘ i NO - domain of g is Integer, co-domain of i is Bool What is the output of the following functional composition funA :: Integer -> Integer funA x = (x * 3)^2 funB :: Integer -> Integer funB y = 4 * (y - 2) (funA.funB) 2 (funA.funB) 3 (funB.funA) 3 Answer: 0 144 316