Programming Concepts: Recursive Techniques
Recursion is a key area in computer science that relies on you being able to solve a problem by the cumulation of solving increasingly smaller instances of the same problem.

An example of recursion in a name is the GNU Operating System, you might well ask what GNU stands for:
- GNU = GNU is Not Unix
Wait a minute, they have defined the name by restating the name!:
- GNU
- GNU is Not Unix
- GNU is Not Unix is Not Unix
- GNU is Not Unix is Not Unix is Not Unix
- GNU is Not Unix is Not Unix is Not Unix is Not Unix
- ad infinitum
Luckily for us, with computer code our recursion should tend towards an end as we are solving increasingly smaller instances of the same problem, we should be tending towards an end. With the GNU example the name always remains the same size, but with the following example there is an end:
|
Example: A recursive story function revise(essay) {
read(essay);
get_feedback_on(essay);
apply_changes_to(essay);
revise(essay) unless essay.complete?;
}
Which is pseudocode to describe the process of revising an essay, the revision process involves reading the essay, getting feedback, applying the changes, then revising the slightly better essay. You keep doing this until the essay is complete. |
Let's take a look at some computer science examples
Factorial example
[edit | edit source]A classic computer example of a recursive procedure is the function used to calculate the factorial of a natural number:
For example:
Did you notice what I did with the final solution? Instead of writing 5 * 4 * 3 * 2 * 1, I used 5! which elicits the same result. Looking back our definition of why recursion is used, we seem to solve big problems by solving smaller instances of the same problem, so factorials are ripe for recursion:
10! = 10 * 9! 9! = 9 * 8! 8! = 8 * 7! 7! = 7 * 6! 6! = 6 * 5! 5! = 5 * 4! 4! = 4 * 3! 3! = 3 * 2! 2! = 2 * 1! 1! = 1
As we can see, each n! is the product of n * (n-1)!. In summary:
| Pseudocode (recursive): |
|---|
function factorial is: |
Now let's have a look at how we would write code to solve this:
function factorial(ByVal n as integer)
if n >= 1 then
return n * factorial(n-1) 'recursive call
else
return 1
end if
end function
sub main()
console.writeline(factorial(10))
end sub
It looks very simple and elegant. But how does it work?
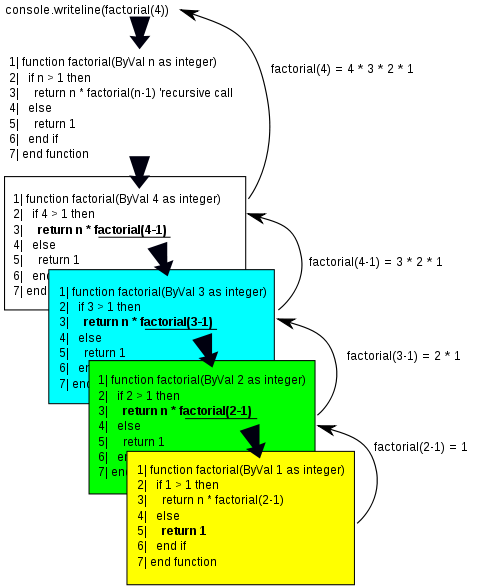
Let's build a trace table and see what happens. This trace table will be different from the ones that you have built before as we are going to have to use a stack. If you haven't read up on stacks you must do so before continuing:
| Function call | n | Return Line |
|---|---|---|
| 1 | 4 |
All is going well so far until we get to line 3. Now what do we do? We'll soon have two values of n, one for Function call 1 and one for Function call 2. Using the trace table as a stack (with the bottom of the stack at the top and the top of the stack at the bottom) we'll save all the data about the function call including its value of n and make note of what line we need to return to when we have finished with factorial(3).
| Function call | n | Return Line |
|---|---|---|
| 1 | 4 | 3 |
| 2 | 3 |
We now have a similar situation to before, let's store the return address and go to factorial(2)
| Function call | n | Return Line |
|---|---|---|
| 1 | 4 | 3 |
| 2 | 3 | 3 |
| 3 | 2 |
We now have a similar situation to before, let's store the return address and go to factorial(1)
| Function call | n | Return Line | Return Value |
|---|---|---|---|
| 1 | 4 | 3 | |
| 2 | 3 | 3 | |
| 3 | 2 | 3 | |
| 4 | 1 | 1 |
Now we have another problem, we have found an end to the factorial(1). What line do we go to next? As we are treating our trace table as a stack we'll just pop the previous value off the top and look at the last function call we stored away, that is function call 3, factorial(2), and we even know what line to return to, line 3:
return 2 * factorial(1)
We know that factorial(1) = 1 from the previous returned value. Therefore factorial(2) returns 2 * 1 = 2
| Function call | n | Return Line | Return Value |
|---|---|---|---|
| 1 | 4 | 3 | |
| 2 | 3 | 3 | |
| 3 | 2 | 3 | 2 |
Again we'll pop the last function call from the stack leaving us with function call 2, factorial(3) and line 3.
return 3 * factorial(2)
We know that factorial(2) = 2 from the previous returned value. Therefore factorial(3) returns 3 * 2 = 6
| Function call | n | Return Line | Return Value |
|---|---|---|---|
| 1 | 4 | 3 | |
| 2 | 3 | 3 | 6 |
Again we'll pop the last function call from the stack leaving us with function call 1, factorial(4) and line 3.
return 4 * factorial(3)
We know that factorial(3) = 6 from the previous returned value. Therefore factorial(4) returns 4 * 6 = 24
| Function call | n | Return Line | Return Value |
|---|---|---|---|
| 1 | 4 | 3 | 24 |
We reach the end of function call 1. But where do we go now? There is nothing left on the stack and we have finished the code. Therefore the result is 24.
Fibonacci number example
[edit | edit source]
Another good example is a method to calculate the Fibonacci numbers. By definition, the first two Fibonacci numbers are 0 and 1, and each subsequent number is the sum of the previous two.:
For example, take the 6th number, 5. This is the sum of the 5th number, 3, and the 4th number, 2.
In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recursive statement
with the first two values being
Let's try and create a code version of this:
| Answer: | ||
function fib(n as integer)
select case n
case 0
return 0
case 1
return 1
case else
return fib(n-1) + fib(n-2)
end select
end function
|
||
Recursion summary
[edit | edit source]Recursion does have some issues though, consider how much data we had to store on the stack for just 4 function calls. If we were to perform 1000, the memory used would be incredibly large.
|
Exercise: Recursion Define recursion: Answer: Defining a sub routine in terms of itself Give the output of the following recursive function call recur(6): function recur(ByVal n as integer)
console.writeline(n)
if n > 0 then
recur(n-1)
else
return 0
end if
end function
Answer: 6 5 4 3 2 1 0 Give the output of the following recursive function call recur(4): function recur(ByVal n as integer)
if n > 0 then
recur(n-1)
else
return 0
end if
console.writeline(n)
end function
Answer: 1 2 3 4 Give the output of the following recursive function call recur(6): function recur(ByVal n as integer)
if n <= 10 then
recur(n+1)
else
return 0
end if
console.writeline(n)
end function
Answer: 10 9 8 7 6 Draw a trace table for the following recursive function Answer: Name one benefit and one drawback of recursive solutions: Answer:
|
References
[edit | edit source]- ↑ thesecretmaster on StackExchange https://cseducators.stackexchange.com/questions/17/analogy-for-teaching-recursion







