A-level Chemistry/OCR (Salters)/Molecular geometry
The shapes of molecules is the title of Section 3.3 in Chemical Ideas and it covers the topic of molecular geometry.
Introductory examples
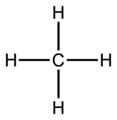
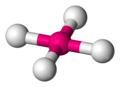
[edit | edit source]Methane molecule
[edit | edit source]-
dot-cross diagram -
bond-line diagram -
ball-and-stick model
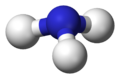
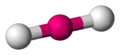
Ammonia molecule
[edit | edit source]-
dot-cross diagram -
bond-line diagram -
ball-and-stick model with lone pairs displayed -
ball-and-stick model without lone pairs displayed
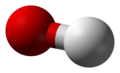
Water molecule
[edit | edit source]-
dot-cross diagram -
bond-line diagram -
ball-and-stick model with lone pairs displayed -
ball-and-stick model without lone pairs displayed
Hydrogen fluoride molecule
[edit | edit source]-
dot-cross diagram -
bond-line diagram -
ball-and-stick model with lone pairs displayed -
ball-and-stick model without lone pairs displayed
Polyhedra
[edit | edit source]Tetrahedra
[edit | edit source]You have probably come across tetrahedra before in maths, although you most likely called them triangle-based pyramids. Tetrahedra have four vertices (corners), four faces and six edges. Each face is an equilateral triangle.
The tetrahedron is one of the most important shapes in chemistry because a very great many molecules contain them. Tetrahedral molecules don't actually contain little pyramids. What they do contain is a central atom bonded to four other atoms. The four atoms surrounding the central atom occupy positions that you can imagine as the vertices of a tetrahedron.
In the image gallery below, the central atom is coloured magenta and the surrounding atoms are coloured white.
-
a tetrahedral molecule -
to see the tetrahedron, connect the surrounding atoms with lines -
the lines form the edges of the tetrahedron -
tetrahedral angle ≈ 109.5° -
chemists represent tetrahedra using hashed and wedged bonds -
this is how chemists represent methane -
this 'flat' representation - GCSE-style - is simpler but less realistic
The angle between any two bonds in a tetrahedral molecule is approximately 109.5°. The tetrahedral angle can be calculated as accurately as required because it is equal to cos−1(–⅓).
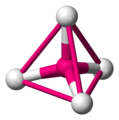
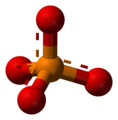
Octahedra
[edit | edit source]You may or may not have met an octahedron before. Octahedra have six vertices (corners), eight faces and twelve edges. Each face is an equilateral triangle.
Octahedra are very important in chemistry because many transition metal-based molecules are octahedral.
-
an octahedral molecule -
to see the octahedron, connect the surrounding atoms with lines -
the lines form the edges of the octahedron -
octahedral angle = 90° exactly -
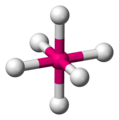
chemists represent octahedra using hashed and wedged bonds -
this is how chemists represent sulfur hexafluoride, SF6 -
a ball-and-stick model of SF6
Common molecular geometries
[edit | edit source]-
linear -
bent -
trigonal planar -
pyramidal -
square planar -
tetrahedral -
trigonal bipyramidal -
octahedral
Further examples
[edit | edit source]Example molecules
[edit | edit source]Example ions
[edit | edit source]Molecular geometry and lone pairs
[edit | edit source]You can use the so-called AXE method to calculate the shape of a molecule. It is based on molecules that have a central atom, which we label A. Atoms or groups bonded to A are labelled X. Lone pairs are labelled E. A molecule with three lone pairs and two atoms/groups bonded to it would be denoted AX2E3. The table below shows how X and E and molecular shape are related.
Valence shell electron pair repulsion theory (VSEPR) is used to predict the shape of a molecule once X and E are known. This sounds more complicated than it is. You consider any X's and E's to be regions of charge that position themselves as far apart from each other as possible, in order to minimize the forces of electrostatic repulsion between each other.
| AXE label | X (substituents) |
E (lone pairs) |
Shape | 2D diagram lone pairs shown |
2D diagram lone pairs not shown |
3D model lone pairs shown |
3D model lone pairs not shown |
Examples |
|---|---|---|---|---|---|---|---|---|
| AX1E0 | Linear | H2 | ||||||
| AX1E1 | Linear | CN− | ||||||
| AX1E2 | Linear | 
|

|
O2 | ||||
| AX1E3 | Linear | 
|

|
HCl | ||||
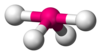
| AX2E0 | Linear | BeCl2 HgCl2 CO2 | ||||||
| AX2E1 | Bent | 
|

|

|
NO2− SO2 O3 | |||
| AX2E2 | Bent | 
|
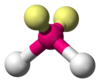
|

|
H2O H2S OF2 | |||
| AX2E3 | Linear | 
|

|
XeF2 I3− | ||||
| AX3E0 | Trigonal planar | 
|

|

|

|
BF3 CO32− NO3− SO3 | ||
| AX3E1 | Trigonal pyramidal | 
|

|

|

|
NH3 PCl3 | ||
| AX3E2 | T-shaped | 
|

|

|

|
ClF3 BrF3 | ||
| AX4E0 | Tetrahedral | 
|

|
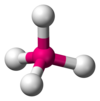
|

|
CH4 NH4+ PO43− SO42− ClO4− | ||
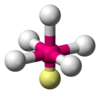
| AX4E1 | Seesaw | 
|

|

|
|
SF4 | ||
| AX4E2 | Square Planar | 
|

|

|
XeF4 | |||
| AX5E0 | Trigonal Bipyramidal | 
|

|

|

|
PCl5 | ||
| AX5E1 | Square pyramidal | 
|

|
|
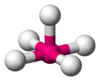
|
ClF5 BrF5 | ||
| AX5E2 | Pentagonal planar | 
|

|

|
XeF5- | |||
| AX6E0 | Octahedral | 
|

|
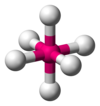
|
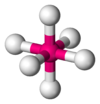
|
SF6 | ||
| AX6E1 | Pentagonal pyramidal | 
|

|

|

|
IF6- | ||
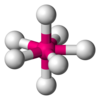
| AX7E0 | Pentagonal bipyramidal | 
|

|
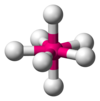
|
|
IF7 | ||
| AX8E0 | Square antiprismatic | 
|

|
IF8- | ||||
| AX8E1 | Distorted square antiprismatic | 
|
XeF82- | |||||
| AX9E0 | Tricapped trigonal prismatic OR capped square antiprismatic | 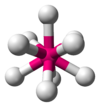
|

|
ReH92- (tricapped trigonal prismatic) |