#This source code is public domain
#Author: Christian Schirm
import numpy, scipy.spatial
import matplotlib.pyplot as plt
def covMat(x1, x2, covFunc, noise=0): # Covariance matrix
cov = covFunc(scipy.spatial.distance_matrix(numpy.atleast_2d(x1).T, numpy.atleast_2d(x2).T))
if noise: cov += numpy.diag(numpy.ones(len(cov))*noise)
return cov
def interpol(x_known, y_known, x_unknown, covFunc, noise=0, sigmaPrior=1):
Ckk = covMat(x_known, x_known, covFunc)
Cuk = covMat(x_unknown, x_known, covFunc, noise=0)
y_unknown = numpy.dot(Cuk, numpy.dot(numpy.linalg.inv(Ckk), y_known))
CkkInv = numpy.linalg.inv(Ckk)
sigma_unknown = numpy.sqrt(sigmaPrior * sigmaPrior - numpy.diag(numpy.dot(Cuk, numpy.dot(CkkInv, Cuk.T))))
return y_unknown, sigma_unknown
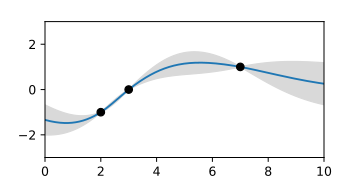
covFunc = lambda d: numpy.exp(-(d**1.9/8.)) # Covariance function
x_known = numpy.array([2,3,7])
y_known = numpy.array([-1,0,1])
x_unknown = numpy.linspace(0, 10, 300)
y_unknown, sigma_unknown = interpol(x_known, y_known, x_unknown, covFunc)
Ckk = covMat(x_known, x_known, covFunc, noise=0.0)
Cuu = covMat(x_unknown, x_unknown, covFunc, noise=0.00)
CkkInv = numpy.linalg.inv(Ckk)
Cuk = covMat(x_unknown, x_known, covFunc, noise=0)
m = 0 #numpy.mean(y)
covPost = Cuu - numpy.dot(numpy.dot(Cuk,CkkInv),Cuk.T)
y_unknown = numpy.dot(numpy.dot(Cuk,CkkInv),y_known)
fig = plt.figure(figsize=(4.0,2))
plt.plot(x_unknown, y_unknown, label=u'Prediction')
sigma = numpy.sqrt(numpy.diag(covPost))
plt.plot(x_known, y_known,'ko')
plt.fill_between(x_unknown.ravel(), y_unknown - sigma, y_unknown + sigma, color = '0.85')
plt.axis([0,10,-3,3])
plt.savefig('Gaussianprocess_posteriorMean.svg')