FHSST Physics/Waves/Properties
Properties of Waves
[edit | edit source]We have discussed some of the simple properties of waves that we need to know. These have just been describing the characteristics that waves have. Now we can progress onto some more interesting and, perhaps, less intuitive properties of waves.
Properties of Waves : Reflection
[edit | edit source]When waves strike a barrier they are reflected. This means that waves bounce off things. Sound waves bounce off walls, light waves bounce off mirrors, radar waves bounce off planes and how bats can fly at night and avoid things as small as telephone wires. etc. The property of reflection is a very important and useful one.
(NOTE TO SELF: Get an essay by an air traffic controller on radar) (NOTE TO SELF: Get an essay by on sonar usage for fishing or for submarines)
When waves are reflected, the process of reflection has certain properties. If a wave hits an obstacle at a right angle to the surface (NOTE TO SELF: diagrams needed) then the wave is reflected directly backwards.
If the wave strikes the obstacle at some other angle then it is not reflected directly backwards. The angle that the waves arrives at is the same as the angle that the reflected waves leaves at. The angle that waves arrives at or is incident at equals the angle the waves leaves at or is reflected at. Angle of incidence equals angle of reflection
|
(2.1) |
: angle of incidence : angle of reflection
In the optics chapter you will learn that light is a wave. This means that all the properties we have just learnt apply to light as well. Its very easy to demonstrate reflection of light with a mirror. You can also easily show that angle of incidence equals angle of reflection.
If you look directly into you see yourself ....
Need to mention that the incident wave, normal to the surface and the reflected wave all lie in the same plane. The same also holds for refraction at a surface.
Phase shift of reflected wave
[edit | edit source]When a wave is reflected from a more dense medium, it undergoes a phase shift. That means that the peaks and troughs are swapped around.
The easiest way to demonstrate this is to tie a piece of string to something. Stretch the string out flat and then flick the string once so a pulse moves down the string. When the pulse (a single peak in a wave) hits the barrier that the string is tied to, it will be reflected. The reflected wave will look like a trough instead of a peak. This is because the pulse had undergone a phase change. The fixed end is like reflection off a more dense medium.
If the end of the string was not fixed, i.e. it could move up and down then the wave would still be reflected but it would not undergo a phase shift.
Properties of Waves : Refraction
[edit | edit source]Sometimes waves move from one medium to another. The medium is the substance that is carrying the waves. In our first example this was the water. When the medium properties change it can affect the wave.
Let us start with the simple case of a water wave moving from one depth to another. The speed of the wave depends on the depth. If the wave moves directly from the one medium to the other than we should look closely at the boundary. When a peak arrives at the boundary and moves across it must remain a peak on the other side of the boundary. This means that the peaks pass by at the same time intervals on either side of the boundary. The period and frequency remain the same! But we said the speed of the wave changes, which means that the distance it travels in one time interval is different i.e. the wavelength has changed.
Going from one medium to another the period or frequency does not change only the wavelength can change.
Now if we consider a water wave moving at an angle of incidence not 90 degrees towards a change in medium then we immediately know that not the whole wave will arrive at once. So if a part of the wave arrives and slows down while the rest is still moving faster before it arrives the angle of the wavefront is going to change. This is known as refraction. When a wave bends or changes its direction when it goes from one medium to the next.
If it slows down it turns towards the perpendicular.
If the wave speeds up in the new medium it turns away from the perpendicular to the medium surface.
When you look at a stick that emerges from water it looks like it is bent. This is because the light from below the surface of the water bends when it leaves the water. Your eyes project the light back in a straight line and so the object looks like it is a different place.
Properties of Waves : Interference
[edit | edit source]If two waves meet interesting things can happen. Waves are basically collective motion of particles. So when two waves meet they both try to impose their collective motion on the particles. This can have quite different results.
If two identical (same wavelength, amplitude and frequency) waves are both trying to form a peak then they are able to achieve the sum of their efforts. The resulting motion will be a peak which has a height which is the sum of the heights of the two waves. If two waves are both trying to form a trough in the same place then a deeper trough is formed, the depth of which is the sum of the depths of the two waves. Now in this case the two waves have been trying to do the same thing and so add together constructively. This is called constructive interference.
If one wave is trying to form a peak and the other is trying to form a trough then they are competing to do different things. In this case they can cancel out. The height of the peak less the depth of the trough will be the resulting effect. If the depth of the trough is the same as the height of the peak nothing will happen. If the height of the peak is bigger than the depth of the trough a smaller peak will appear and if the trough is deeper then a less deep trough will appear. This is destructive interference.
Properties of Waves : Standing Waves
[edit | edit source]When two waves move in opposite directions, through each other, constructive interference happens. If the two waves have the same frequency and wavelength then a specific type of constructive interference can occur: standing waves can form.
Standing waves are disturbances which don't appear to move, they stand in the same place. Lets demonstrate exactly how this comes about. Imagine a long string with waves being sent down it from either end. The waves from both ends have the same amplitude, wavelength and frequency as you can see in the picture below:
To stop from getting confused between the two waves we'll draw the wave from the left with a dashed line and the one from the right with a solid line. As the waves move closer together when they touch both waves have an amplitude of zero:
If we wait for a short time the ends of the two waves move past each other and the waves overlap. Now we know what happens when two waves overlap, we add them together to get the resulting wave.
Now we know what happens when two waves overlap, we add them together to get the resulting wave. In this picture we show the two waves as dotted lines and the sum of the two in the overlap region is shown as a solid line:
The important thing to note in this case is that there are some points where the two waves always destructively interfere to zero. If we let the two waves move a little further we get the picture below:
Again we have to add the two waves together in the overlap region to see what the sum of the waves looks like.
In this case the two waves have moved half a cycle past each other but because they are out of phase they cancel out completely. The point at 0 will always be zero as the two waves move past each other.
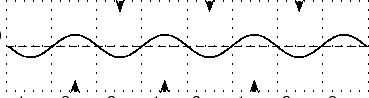
When the waves have moved past each other so that they are overlapping for a large region the situation looks like a wave oscillating in place. If we focus on the range -4, 4 once the waves have moved over the whole region. To make it clearer the arrows at the top of the picture show peaks where maximum positive constructive interference is taking place. The arrows at the bottom of the picture show places where maximum negative interference is taking place.
As time goes by the peaks become smaller and the troughs become shallower but they do not move.
For an instant the entire region will look completely flat.
The various points continue their motion in the same manner.
Eventually the picture looks like the complete reflection through the x-axis of what we started with:
Then all the points begin to move back. Each point on the line is oscillating up and down with a different amplitude.
If we superimpose the two cases where the peaks where at a maximum and the case where the same waves where at a minimum we can see the lines that the points oscillate between. We call this the envelope of the standing wave as it contains all the oscillations of the individual points. A node is a place where the two waves cancel out completely as two waves destructively interfere in the same place. An anti-node is a place where the two waves constructively interfere.
To make the concept of the envelope clearer let us draw arrows describing the motion of points along the line.
Every point in the medium containing a standing wave oscillates up and down and the amplitude of the oscillations depends on the location of the point. It is convenient to draw the envelope for the oscillations to describe the motion. We cannot draw the up and down arrows for every single point!
Reflection from a fixed end
[edit | edit source]If waves are reflected from a fixed end, for example tying the end of a rope to a pole and then sending waves down it. The fixed end will always be a node. Remember: Waves reflected from a fixed end undergo a phase shift.
The wavelength, amplitude and speed of the wave cannot affect this, the fixed end is always a node.
Reflection from an open end
[edit | edit source]If waves are reflected from end, which is free to move, it is an anti-node. For example tying the end of a rope to a ring, which can move up and down, around the pole. Remember: The waves sent down the string are reflected but do not suffer a phase shift.
Wavelengths of standing waves with fixed and open ends
[edit | edit source]Beats
[edit | edit source]If the waves that are interfering are not identical then the waves form a modulated pattern with a changing amplitude. The peaks in amplitude are called beats. If you consider two sound waves interfering then you hear sudden beats in loudness or intensity of the sound.
The simplest illustration is to draw two different waves and then add them together. You can do this mathematically and draw them yourself to see the pattern that occurs.
Here is wave 1:
Now we add this to another wave, wave 2:
When the two waves are added (drawn in coloured dashed lines) you can see the resulting wave pattern:
To make things clearer the resulting wave without the dashed lines is drawn below. Notice that the peaks are the same distance apart but the amplitude changes. If you look at the peaks they are modulated i.e. the peak amplitudes seem to oscillate with another wave pattern. This is what we mean by modulation.
The maximum amplitude that the new wave gets to is the sum of the two waves just like for constructive interference. Where the waves reach a maximum it is constructive interference.
The smallest amplitude is just the difference between the amplitudes of the two waves, exactly like in destructive interference.
The beats have a frequency which is the difference between the frequency of the two waves that were added. This means that the beat frequency is given by
|
(2.2) |
fB : beat frequency (Hz or s-1) f1 : frequency of wave 1 (Hz or s-1) f2 : frequency of wave 2 (Hz or s-1)
Properties of Waves : Diffraction
[edit | edit source]One of the most interesting, and also very useful, properties of waves is diffraction. When a wave strikes a barrier with a hole, only part of the wave can move through the hole. If the hole is similar in size to the wavelength of the wave diffractions occurs. The waves that comes through the hole no longer looks like a straight wave front. It bends around the edges of the hole. If the hole is small enough it acts like a point source of circular waves.
This bending around the edges of the hole is called diffraction. To illustrate this behaviour we start with Huygen's principle.
Huygen's Principle
[edit | edit source]Huygen's principle states that each point on a wavefront acts like a point source or circular waves. The waves emitted from each point interfere to form another wavefront on which each point forms a point source. A long straight line of points emitting waves of the same frequency leads to a straight wave front moving away.
To understand what this means lets think about a whole lot of peaks moving in the same direction. Each line represents a peak of a wave.
If we choose three points on the next wave front in the direction of motion and make each of them emit waves isotropically (i.e. the same in all directions) we will get the sketch below:
What we have drawn is the situation if those three points on the wave front were to emit waves of the same frequency as the moving wave fronts. Huygens principle says that every point on the wave front emits waves isotropically and that these waves interfere to form the next wave front.
To see if this is possible we make more points emit waves isotropically to get the sketch below:
You can see that the lines from the circles (the peaks) start to overlap in straight lines. To make this clear we redraw the sketch with dashed lines showing the wavefronts which would form. Our wavefronts are not perfectly straight lines because we didn't draw circles from every point. If we had it would be hard to see clearly what is going on.
Huygen's principle is a method of analysis applied to problems of wave propagation. It recognizes that each point of an advancing wave front is in fact the center of a fresh disturbance and the source of a new train of waves and that the advancing wave as a whole may be regarded as the sum of all the secondary waves arising from points in the medium already traversed. This view of wave propagation helps better understand a variety of wave phenomena, such as diffraction.
Wavefronts Moving Through an Opening
[edit | edit source]Now if we allow the wavefront to impinge on a barrier with a hole in it, then only the points on the wavefront that move into the hole can continue emitting forward moving waves - but because a lot of the wavefront have been removed the points on the edges of the hole emit waves that bend round the edges.
The wave front that impinges (strikes) the wall cannot continue moving forward. Only the points moving into the gap can. If you employ Huygens' principle you can see the effect is that the wavefronts are no longer straight lines.
Riaan Note: still cant find this image, have to get it from the pdf
For example, if two rooms are connected by an open doorway and a sound is produced in a remote corner of one of them, a person in the other room will hear the sound as if it originated at the doorway. As far as the second room is concerned, the vibrating air in the doorway is the source of the sound. The same is true of light passing the edge of an obstacle, but this is not as easily observed because of the short wavelength of visible light.
This means that when waves move through small holes they appear to bend around the sides because there aren't enough points on the wavefront to form another straight wavefront. This is bending round the sides we call diffraction.
Properties of Waves : Dispersion
[edit | edit source]Dispersion is a property of waves where the speed of the wave through a medium depends on the wavelength. So if two waves enter the same dispersive medium and have different wavelengths they will have different speeds in that medium even if they both entered with the same speed.