Fundamentals of Data Representation: Unsigned binary arithmetic
You should be comfortable with adding, subtracting and multiplying in decimal. Computers need to do the same in binary, and you need to know it for the exam!
Addition
[edit | edit source]Let's look at an example of adding in decimal:
25 +43 --- 68
This is pretty simple, we just add up each column, but what happens if we have can't fit the result in one column. We'll have to use a carry bit:
98 +57 --- 155 11
Hopefully you're good with that. Now let's take a look at how it's done in binary with a very quick example, with a check in denary:
01010 (1010) +00101 (510) ------ 01111 (1510)
This seems pretty straight forward, but what happens when we have a carry bit? Well pretty much the same as in denary:
01011 (1110) +00001 (110) ------ 01100 (1210) 11

|
Exercise: Binary Addition 1010 + 0001 Answer: 1010 +0001 ---- 1011 01001001 + 00110000 Answer: 01001001 +00110000 -------- 01111001 01010100 + 00110000 Answer: 01010100 +00110000 -------- 10000100 01001010 + 00011011 Answer: 01001010 +00011011 -------- 01100101 01111101 + 00011001 Answer: 01111101 +00011001 -------- 10010110 00011111 + 00011111 Answer: 00011111 +00011111 -------- 00111110 10101010 + 01110000 Answer: 10101010 +01110000 -------- 100011010 Note we have some overflow, this will come in useful when doing subtraction |
Multiplication
[edit | edit source]You should hopefully have learnt how to multiply numbers together in decimal when you were at primary school. Let's recap:
12 x 4 -- 8 = 4*2 40 = 4*10–48
And with a more complicated example:
12 x14–8 = 4 * 2 40 = 4 * 10 20 = 10* 2 100 = 10* 10–168
The same principle applies with binary. Let's take a look at an example:
101 x 10 ---- 0 = 0 * 101 1010 = 10 * 101 [or in denary 2 * 5 = 10]
Let's try a more complicated example:
1011 [11] x 111 [7] ---- 1011 = 1 * 1011 10110 = 10 * 1011 101100 = 100 * 1011 ------ now add them together 1001101 = [77 double check with the decimal earlier]
|
Exercise: Binary Multiplication 101 * 10 Answer: 101 x 10 ---- 1010 11 * 11 Answer: 11 x 11 ---- 11 110 ---- 1001 1011 * 101 Answer: 1011 x 101 ------ 1011 101100 ------ 110111 1111 * 111 Answer: 1111 = 15
x 111 = 7
------
1111
11110
111100
------
1101001 = 105
If you multiply a binary number by 2, how many spaces does it move to the left? Answer: 1 If you multiply a binary number by 16, how many spaces does it move to the left? Answer: 4 (as 2^4 = 16) This is a short cut for multiplication in computers, and it uses machine code shift instructions to do this. Don't worry you don't need to know them for this syllabus |
|
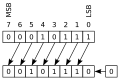
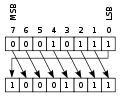
Extension: Bit Shifts If you look at the binary representations of the following numbers you may notice something peculiar: 0001 = 1 0010 = 2 0100 = 4 1000 = 8 Each time we shift the number one space to the left, the value of the number doubles. This doesn't only work for one bit, take a look at this more complicated example. 0001 0101 = 21 0010 1010 = 42 Again, one shift to the left and the number has doubled. On the other hand, one shift to the right halves the value. Computers are notoriously bad at doing multiplication and division, it takes lots of CPU time and can really slow your code down. To try and get past this problem computers can shift the values in registers and as long as multiplication or division is by powers of 2, then the CPU time is reduced as the action takes only one line of Machine Code. There are several types of shifts that processors can perform:
Shifting either left or right, you add a 0 on the empty end.
You maintain the sign bit of the number being shifted. Please note the Logical shift example is also an example of an arithmetic shift as the sign remains the same. You'll find out about sign bits when learning about two's complement
The bit that is pushed off one end appears on the other
|