On 2D Inverse Problems/Kernel of Dirichlet-to-Neumann map
The continuous analog of the matrix representation of a Dirichlet-to-Neumann operator for a domain is its kernel. It is a distribution defined on the Cartesian product of the boundary of the domain w/itself, such that if
then where and parametrize the boundary w/arclength measure.
For the case of the half-plane w/constant unit conductivity the kernel can be calculated explicitly. It's a convolution, because the domain in consideration is shift invariant:
where k is a distribution on a line. Therefore, the calculation reduces to solving the Dirichlet problem for a -function at the origin and taking outward derivative at the boundary line.
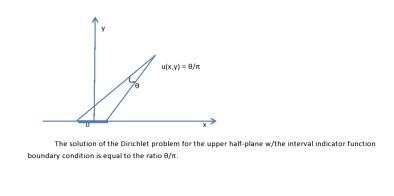
Exercise (**). Complete the calculation of the kernel K for the half-plane to show that off the diagonal.
Exercise (*). Prove that for rotation invariant domain (disc w/ conductivity depending only on radius) the kernel of Dirichlet-to-Neumann map is a convolution.
The Hilbert transform gives a correspondence between boundary values of a harmonic function and its harmonic conjugate. where is an analytic function in the domain.
For the case of the complex upper half-plane the Hilbert transform is given by the following formula:
Exercise (*). Differentiate under the integral sign the formula above to obtain the kernel representation for the Dirichlet-to-Neumann operator for the half plane.
To define discrete Hilbert transform for a planar network, the network together w/its dual is needed.










