Transportation Economics/Pricing
Pricing
Rationales for Pricing
[edit | edit source]Roadway congestion, air pollution from cars, and the lack of resources to finance new surface transportation options present challenges. Road pricing, charging users a monetary toll in addition to the amount of time spent traveling, has been suggested as a solution to these problems. While tolls are common for certain expensive facilities such as tunnels and bridges, they are less common on streets and highways. A new generation of private toll roads are being deployed in the United States and elsewhere. There have been a few trials of areawide pricing schemes, such as in Singapore, London, and Stockholm, and many others proposed but not implemented.
In short pricing can accomplish several objectives
- Revenue
- Congestion management - Traffic congestion is very common in large cities and on major highways. It is time consuming and imposes a significant amount of uncertainty and aggravation on passengers and freight transportation. Most of the cost of traffic congestion caused by travelers' selfish behaviors (see discussion of Route Choice), because they impose delays on others and do not pay the full marginal cost of their trips. In economic terms, a negative externality is created. In order to solve this problem some economist proposed that there should be a tax on congestion. In the first edition of his textbook, The Economics of Welfare, Pigou (1920) argued for a tax on congestion and thereby launched the literature on congestion pricing. Most economists support congestion pricing as a good way to relieve the dilemma, while many have been concerned about the details of implementation. Congestion charges allocate scarce road capacity in congested areas and peak times. Electronic Toll Collection (ETC) and Automated Vehicle Identification (AVI) technologies allow this to be done without delaying travelers.
- Pavement management - Pavement damage depends on vehicle weight per axle, not total vehicle weight - the damage power rises exponentially to the third power with the load per axle (e.g., a rear axle of a typical 13-ton van causes over 1000 times as much damages that of a car). In order to reflect the pavement damage costs more accurately, Small and Winston (1989) propose a "graduated per-mile tax based on axle weight". This would give truckers (truck manufactuers) an incentive to reduce axle weights by shifting to trucks with more axles, extending pavement life and reducing highway maintenance. The fuel tax currently in place provides truckers with the opposite incentives: the tax rises with a vehicle's axles, since trucks with more axles require larger engines and get lower fuel economy. They pointed out that the pavement thickness guidelines of the American Association of State Highway and Transportation Officials (AASHTO) fails to incorporate economic optimization into the design procedure. For example, by increasing rigid concrete pavement thickness only by 2.6 inches from currently 11.2 inches to 13.8 inches would more than double the life of the pavement.
- Off-loading costs or reallocating costs (changing who bears burden) - Highway cost allocation studies periodically attempt to update the amount of burden for roads borne by cars and various classes of trucks, but they only have two policy tools (gasoline and diesel fuel taxes) to do the job. A more robust pricing strategy could make charges far more directly proportional to source.
- Changing energy supply indicates declining gas tax revenue
- Encourage alternatives to driving
There are reasons that road pricing is not more widespread. Until recently, technical issues were dominant, toll collection added considerable delay and greatly reduced net revenue with the need for humans sitting in toll booths. However, advances in automatic vehicle identification and tolling have enabled toll collection, without human operators, at full speed. Other issues are fundamentally political: concerns over privacy, equity, and the perception of double taxation. Privacy concerns, though political, may have a technical solution, with the use of electronic money, which is not identified with its owner, rather than credit or debit cards or automatic identification and billing of vehicles. Equity issues, the belief that there will be winners and losers from the new system, may not be entirely resolvable. Though it can be shown that under certain circumstances road pricing has a net benefit for society as a whole, unless a mechanism exists for making a sufficient majority of road users and voters benefit, or perceive benefit, this concern is a roadblock to implementation. Similarly, people may believe that they have paid for roads already through gas taxes and general revenue, and that charging for them is akin to double taxation. Unless users can be convinced that the revenue raised is for maintenance and expansion, or another convincing public purpose, the political sell will be difficult. Widespread road pricing may require changes in the general transportation financing structure and a clear accounting of the benefits will need to be provided.
Theory of Congestion Pricing
[edit | edit source]
Whenever a scarce and valued good such as road use is free or under priced, demand will outstrip supply. An illustration pertaining to road use is evident by the queues and traffic jams that occur when the number of motorists attempting to use a section of roadway at the same time exceeds the road’s capacity. Expanding capacity to meet peak demand results in wasteful excess capacity during non-peak periods unless the peak users are charged the full cost of the expansion. If we look at long-distance telephone service, allocation is determined with a market mechanism by charging a premium for a call during peak periods and by offering a discount during off peak periods. Consumers appear to accept a market-based system for allocating demand in long-distance telephone service and the system suggests this policy works.
In the case of roads, demand is allocated by congestion. The excess demand for road use during peak periods causes congestion. Economists believe that travel behavior is directed by the out-of-pocket expense of a trip plus the value of time that is required. Some motorists do shift their time of travel when congestion gets bad enough, but not enough motorists shift to entirely alleviate the congestion. The number of motorists that do shift their time of travel will never be sufficient to reduce congestion because -without some sort of pricing or rationing of road use- motorists using the road during peak periods do not have to pay for the delays they cause each other.
Making motorists pay for the delays they caused others by making their trips rather than just their personal costs would lead some to make other choices. Motorists may decide to change their time of travel, carpool, or use public transportation. Congestion pricing would allow motorists to make peak-period trips under less congested conditions, but only if they are willing to pay for the delays they impose on each other. The price would be set at a level that reduces congestion to its most efficient level, which can be shown to be the full monetary and time cost for using a segment of road capacity during the peak period.
Decisions made by road users about where and when to use their vehicles are made by comparing the benefits they will receive from using the road with the costs to themselves. These costs do not include the costs they impose on other travelers or on society as a whole, such as congestion and environmental damage. The results from this type of behavior are trips being made in which benefits to the motorist are less than the costs to society. There is more traffic than can be justified and is not efficiently located in time and capacity. If people are charged for the costs they impose on others because of their travel decisions, then that pattern of travel which results in optimal efficiently will occur.
Alternative Revenue Mechanisms
[edit | edit source]Road user charging may be more or less direct. Generally, indirect methods of road charges are related to vehicle ownership and usage. Examples would be fixed charges for owning a car -purchase tax for buying a new vehicle and annual licensing renewals- and variable charges on car usage -taxes on tires oil and fuel.
Indirect methods of road charging, such as fuel taxes, are the most commonly used in today’s society because of the high volume of usage and ease of collection. However, revenue methods like fuel taxes rarely channel funds directly into a road or transportation fund that is specifically for highway maintenance or development. Where there is congestion caused by multiple road users, drivers impose a marginal social cost in terms of delay and higher operating costs on other uses, for which they are not being charged.
Direct charging involves monitoring the actual time or distance of vehicle travel and charging appropriately. There are many ways in which to carry out direct charging. With the development of electronic technology, both off-vehicle and now in-vehicle charging mechanisms can be implemented. Off-vehicle mechanisms are devices like manual toll collection booths, coin operated machines, and road side auto-scanners. In-vehicle mechanisms are magnetic cards, smart cards, and transponders.
Congestion pricing could take several forms. The most straightforward example would be to add an extra fee to an existing toll, or to add a peak fee on an untolled route or bridge. The charge could be a simple peak premium price or off-peak discount received, or the charge could vary according to the demand imposed on a facility at a specific time.
In practice, congestion pricing could take six forms:
- Point pricing, In which a highway user passing a point at a specific time is charged a fee for passing that point regardless of the distance traveled on a specified route;
- Cordon pricing, in which users wishing to enter a congested area are charged fees at each entry point;
- Zone pricing, in which users traveling within a cordoned area also pay a fee;
- Higher charges for parking in congested areas, with particular emphasis on parking during the most congested period;
- Congestion-specific charges, in which users would be charged for both the amount of time spent and distance traveled.
The policies have different implications for demand. General taxes cannot be expected to reduce demand for travel in particular. Transportation specific taxes should reduce demand to a limited extent, but will not reduce demand on targeted road links, such as congested facilities. A cordon toll will reduce demand crossing the cordon, but by its nature is less targeted than “perfect tolls”. While different finance mechanisms have different implications for how they affect demand, they also have different costs of collection. It has historically been true that the more targeted the mechanism, the more costly. However, with the advent of wider use of electronic toll collection, those historical truisms may be altered. Varying the level of jurisdiction administering the policy changes the perception of welfare. Local governments are responsible to local citizens - their constituents, and tend not to concern themselves with the welfare of non-local residents. Therefore the incentive structure facing different layers of government needs to be distinguished. The welfare resulting from implementation when roads are owned and operated by a state may differ from the welfare if the same financing mechanism were implemented by a regional metropolitan planning organization that owned and operated the roads and could retain toll revenue. Similarly, the metropolitan planning organization differs from the county. The key reasons for these differences relate to who pays the tolls, and whether or not the (or to what extent) toll-payers reside within the boundaries of the local governmental agency. A county’s concern for the economic welfare of non-county residents is minimal, as is a metropolitan regions concern for residents of other areas. Decentralization of decision making can thus influence the chosen policy.
Effects of Congestion Pricing
[edit | edit source]The evidence from past changes in bridge and turnpike tolls demonstrates that motorists do respond to changes in price. In referring to the price elasticity of individual demand for transportation, analyses suggest an elasticity of approximately -0.10 to -0.15 as a lower limit and -0.3 to -0.4 as an upper limit depending on the charge, the current costs of travel, and the capacity of alternative roads and transit systems. There will be a decline in demand following a price increase, but consumer demand for road use is strong enough that the percentage decline in demand will not be as large as the percentage increase in price.
There are many possible changes in travel choice, including:
- Route, changing from tolled to untolled routes or to faster tolled routes.
- Time, changing to earlier or later departures to avoid tolls or tolled periods.
- Mode, changing to or away from carpools, transit, or other modes.
- Destination, changing to a closer location for non-work activities.
- Location, moving home or workplace to reduce the commute.
- Sequence, linking trips by combining multiple errands on a single trip.
- Frequency, reducing the number of less important trips
- Presence, conducting activities by telecommuting to decrease work related trips.
- Ownership, Motorists may also forgo ownership of automobiles to bypass toll charges.
Congestion pricing on highways would have broad effects on the entire transportation system by shifting the demand for transportation services away from peak period highway use by solo drivers. A reduction in the incentives to drive during peak periods would shift some traffic to the off-peak, which would increase the efficiency of the road system - therefore, reduce the demand for additional capacity. Some motorists would continue to drive during the peak but would elect to share rides with others or change the destinations of their trips. Sharing rides with others would also increase the efficiency in which the system is used by increasing the number of people per vehicle during peak periods.
Some motorists would shift to transit. The improvement in traffic flows that would result from congestion pricing would improve service reliability and speed, therefore, making transit more attractive than the automobile. The increase in use of transit would increase revenues. These revenues could be put towards increasing service frequency or route coverage. Congestion pricing would also reduce demand for new highway development. This would decrease the demand for capital expenditure on road development in response to growing population and travel demand.
Unpacking
[edit | edit source]
The top part of Figure 2 shows schematically the travel time to a driver (short run average cost) at a bottleneck or on a capacitated link resulting from various levels of approach flow. The travel time function relates travel time (or delay) and approach traffic flow. The greater the approach flow, the higher the travel time. At flows below capacity (level of service A (SA) or B (SB)), traffic flows smoothly, while at high approach flows, those above capacity, traffic is stop and start and is classified as level of service E (SE) or F (SF).
The bottom part of Figure 2 shows schematically the implicit demand for travel on a link as a function of the travel time. All else equal (for instance the price charged to users), demand to travel on a link at level of service A (DA) is higher than demand at level of service F (DF). However the demand and the travel time on a link are not independent, as shown in Figure 2(A).
So the implicit demand and revealed demand are not identical, rather the revealed demand is formed by projecting the travel time at a given flow onto the implicit demand curves. So for instance, when the price charged users is high, the revealed demand coincides with the implicit demand at level of service A (DA). As the prices are lowered, the revealed demand crosses the implicit demand curve at level of service B (DB), then DC, DD, DE and finally at a zero money price it crosses DF. While the actual prices that generate specific demand levels vary from place to place with local circumstances, demand preferences, and market conditions, the general trend (higher prices gives lower approach flow gives better level of service) is simply an application of the law of demand from economics along with traffic flow theory.
In other words, the change in welfare with congestion pricing depends not only on both the change in price and quantity, but also on the change in reservation price. The reservation price is the amount travelers would be willing to pay at a given level of service. And at better levels of service, travelers (and potential travelers) have a higher reservation price.
Welfare Analysis
[edit | edit source]
The movement along the revealed demand curve follows the shape of the curve shown above because of the relationship between traffic flow (quantity demanded) and travel time. Assume for instance that each level of service category represents a one-minute increase in travel time from the immediately better travel time. So in the graph, let the level of service for a one minute trip be denoted SA , and for a six minute trip, SF. The amount of traffic necessary to move from 1 minute to 2 minutes exceeds the amount to move from 2 to 3 minutes. In other words, there is a rising average (and thus marginal) cost in terms of time.
The concepts in Figure 2 can be used to develop the welfare analysis shown in Figure 3. There are several areas of interest in Figure 3. The first is defined by the lower left triangle (the blue + green) (triangle VOZ) which is the consumer surplus when the road is unpriced. The second is the producer surplus (profit) to the road authority when the road is priced, illustrated by the rectangle formed in the lower left (yellow + green) (rectangle OVWY). The third is the consumer surplus when the road is priced, shown in gray (triangle UVW). This consumer surplus represents a higher reservation price than the other because the level of service is better when flow is lower.
That first area needs to be compared to the sum of the second and third areas. If the sum of the second and third areas (OUWY) is larger than the first (OVZ), then pricing has higher welfare than remaining unpriced. Similarly, two price levels can be compared. In other words, the welfare gain from pricing is equal to the yellow + gray area (VUWX) minus the blue area (XYZ). In this particular figure, consumer’s surplus is maximized when the good is free, but overall welfare (including producer’s surplus) is not. Whether consumer’s surplus is in fact higher in a given situation depends on the slopes of the various demand curves.
The greatest welfare is achieved by maximizing the sum of the producer’s surplus rectangle and the consumer’s surplus “triangle” (it may not be a true triangle). This must recognize that the consumers surplus triangle’s hypotenuse must follow an underlying demand curve, not the revealed demand curve. Differentiating the level of service (for instance, providing two different levels of service at two different prices) may result in higher overall welfare (though not necessarily higher welfare for each individual).
Use of the Revenue
[edit | edit source]How welfare is measured and how it is perceived are two different things. If the producer’s surplus is not returned to the users of the system somehow the users will perceive an overall welfare gain as a personal loss because it would be acting as an additional tax. The money can be returned through rebates of other taxes or reinvestment in transportation. It should be noted that the entire argument can be made in reverse, where consumer and producers surplus are measured in time rather than money, and the level of service is the monetary cost of travel. This however has less practical application.
Pricing and Cost Recovery
[edit | edit source]In low volume situations, those that are uncongested, it is unlikely that the revenue from marginal cost congestion pricing will recover long term fixed costs. This is because the marginal impacts of an additional car when volume is low is almost zero, so that additional revenue which can be raised with marginal cost pricing is also zero. Imagine a road with one car - the car’s marginal impact is zero, a marginal cost price would also be zero, its revenue would thus be zero, which is less than the fixed costs.
Add a second car, and marginal impacts are still nearly zero - a phenomenon which remains true until capacity is approached.
Vickery’s Types of Congestion
[edit | edit source]- Simple interaction - light traffic, one car blocked by another, delay is proportional to Q^2
- Multiple interaction - 0.5 < V/C < 0.9
t actual time, to freeflow time, K ~ 3-5
- Bottleneck see below
- Triggerneck - overflow affects other traffic
- Network and Control - Traffic control devices transfer delay
- General Density - high traffic level in general
Marginal Cost Pricing
[edit | edit source]Transportation is a broad field, attracting individuals with backgrounds in engineering, economics, and planning, among others who don’t share a common model or worldview about traffic congestion. Economists look for received technological functions that can be analyzed, but risk misinterpreting them. Engineers seek basic economic concepts to manage traffic, which they view as their own purview. These two fields intersect in the domain of congestion pricing. However many engineers view pricing with suspicion, believing that many economists are overstating its efficacy, while the economists are frustrated with engineering intransigence, and consider engineers as lacking understanding of basic market principles.
This section applies the microscopic model of traffic congestion that to congestion pricing, and allows us to critique the plausibility of several economic models of congestion that have appeared in the literature.
This section uses the idea of queueing and bottlenecks to explain congestion. If there were no bottlenecks (which can be physical and permanent such as lane drops or steep grades, or variable such as a traffic control device, or temporary due to a crash), there would be very little congestion. Vehicles interacting on an uncongested road lead to relatively minimal delays and are not further considered (Vickery 1969, Daganzo 1995) . We define congestion, or the congested period, to be the time when there is queueing. This exceeds the time when arrivals exceed departures, as every vehicle has to wait for all previous vehicles to depart the front of the queue before it can.
A previous section developed the queueing model of congestion.
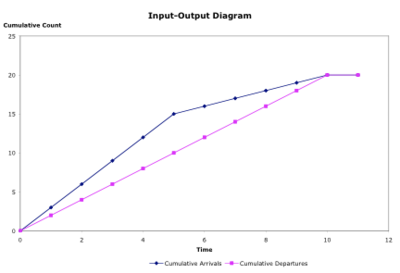

What is the implication of our queueing models for marginal cost pricing?
First, the use of hourly average time vs. flow functions such as the Bureau of Public Roads function, (which we introduced in the discussion of route choice (which approximates the hourly average delay from a queueing model) ignores that different vehicles within that hour have different travel times. They are at best useful for coarse macroscopic analyses, but should never be applied to the level of individual vehicles.
Second, travel time for a vehicle through a bottleneck depends on the number of vehicles that have come before, but not on the number of vehicles coming after. Similarly, the marginal delay that a vehicle imposes is only imposed on vehicles that come after. This implies that the first vehicle in the queue imposes the highest marginal delay, and the last vehicles in the queue have the lowest marginal delay. A marginal delay function that looks like figure on the right (bottom) is generated from the typical input-output diagram shown on the figure on the right (top). If marginal cost were equal to the marginal delay, then our pricing function would be unusual, and perhaps unstable. The instability might be tempered by making demand respond to price, rather than assuming it fixed (Rafferty and Levinson 2003), and by recognizing the stochastic nature of arrival and departure patterns, which would flatten the arrival curve to more closely resemble the departure curve, and thereby flatten the marginal delay curve.
However, the idea that the first vehicle "causes" the delay is a controversial point. Economists will sometimes argue Coase’s position (1992) – that it takes two to have a negative externality, that there would be no congestion externality but for the arrival of the following vehicles. Coase is, of course, correct. Moreover, they would note that charging a toll to the following vehicle will discourage that vehicle from coming and might also eliminate the congestion externality. This may also be true. This would however be charging the sufferer of congestion twice (once in terms of time, a second in terms of toll), while the person with the faster trip (earlier in the queue) wouldn’t pay at all. Further, it is the followers who have already internalized the congestion externality in their decision making, so tolling them is charging them twice, in contrast to charging the leaders. Given that charging either party could eliminate the externality, it would be more reasonable to charge the delayer than the delayed, which is much like the “polluter pays principle” advocated by environmentalists. It would also be more equitable, in that total costs (congestion delay + toll) would now be equalized across travelers. The disadvantage of this is that the amount of the delay caused is unknown at the time that the first traveler passes; at best it can be approximated.
Implicitly, this privileges the “right to uncongested travel” over the “right to unpriced travel”. That is a philosophical question, but given that there is to be some mechanism to finance highways, we can eliminate the notion of unpriced travel altogether, the remaining issue is how to implement financing: with insensitive prices like gas taxes or flat tolls or with time-dependent (or flow-dependent) congestion prices.
The marginal cost equals marginal delay formulation does ignore the question of schedule delay. There are practical reasons for not including schedule delay in a marginal cost price. Unlike delay, schedule delay is not easily measured. While a road administrator can tell you from traffic counts how much delay a traveler caused, the administrator has no clue as to how much schedule delay was caused. Second, if the late (early) penalty is large, then it dominates scheduling. Travelers can decide whether they would rather endure arriving early (without delay) or arriving on time, with some delay (or some combination of the two), presumably minimizing their associated costs. If they choose the delay, it is the lower cost alternative. That lower cost is the one they suffer, and thus that serves as a lower bound on the marginal cost to attribute to other travelers. If they choose schedule delay (which then becomes the cost they face) and avoid the delay, they are affected as well by other travelers, but in a way that is unknown to pricing authorities. They are “priced out of the market”, which happens all the time. In short, endogenizing schedule delay would be nice, but requires more information than is actually available.
Profit Maximizing Pricing
[edit | edit source]A realistic network of highway links is not, in the economists' terminology, perfectly competitive. Because a link uniquely occupies space, it attains some semblance of monopoly power. While in most cases users can switch to alternative links and routes, those alternatives will be more costly to the user in terms of travel time. Theory suggests that excess profits will attract new entrants into a market, but the cost of building a new link is high, indicating barriers to entry not easily overcome.
Although roads are generally treated as public goods, they are both rivalrous when congested and in many cases excludable. This indicates that it is feasible to consider them for privatization. The advantages often associated with privatization are several: increasing the efficiency of the transportation system through road pricing, providing incentives for the facility operator to improve service through innovation and entrepreneurship, and reducing the time and cost of building and expanding infrastructure.
An issue little addressed is implementation. Most trials of road pricing suppose either tolls on a single facility, or area-wide control. Theoretical studies often assume marginal cost pricing on links, and don't discuss ownership structure. However, in other sectors of the economy, central control of pricing either through government ownership or regulation has proven itself less effective than decentralized control for serving customer demands in rapidly changing environments. Single prices system-wide don’t provide as much information as link-specific prices. Links which are priced only at marginal cost, the optimal solution in a first-best, perfectly competitive environment, constrain profit. While in the short-term, excess profit is not socially optimal, over the longer term, it attracts capital and entrepreneurs to that sector of the economy. New capital will both invest more in existing technology to further deploy it and enter the sector as competitors trying to gain from a spatial monopoly or oligopoly. Furthermore, new capitalists may also innovate, and thereby change the supply (and demand) curves in the industry.
By examining road pricing and privatization from a decentralized point of view, the issues associated with a marketplace of roads can be more fully explored, including short and long term distributional consequences and overall social welfare. The main contribution of this research will be to approach the problem from a theoretical and conceptual level and through the conduct of simulation experiments. This analysis will identify salient empirical factors and critical parameters that determine system performance. To the extent that available data from recent road pricing experiments becomes available, it may be used to compare with the results of the model.
Case 1. Simple Monopoly
[edit | edit source]The simplest example is that of a monopoly link,
The link has elastic demand :
here given by a linear equation:
for all and
The objective of the link is to maximize profit . Here we assume no congestion effects. Profit is maximized when the first derivative is set to zero and the second derivative is negative. Giving the following first order conditions (f.o.c.):
Checking second order conditions (s.o.c.), we find them to be less than zero, as required for a maximum.
For this example, if and , gives , and . This situation clearly does not maximize social welfare, defined as the sum of profit and consumer surplus. Consumer surplus at for this demand curve is 125,000, giving a social welfare (SW) of 375,000. Potential social welfare, maximized at (when links are costless), would be , all of which comes from consumer surplus.
Case 2. Monopolistic Perfect Complements
[edit | edit source]In a second simple example, we imagine two autonomous links, and , which are pure monopolies and perfect complements, one cannot be consumed without consuming (driving on) the other. The links are in series.
In this case, demand depends on the price of both links, so we can illustrate by using the following general expression, and a linear example :
Again we assume no congestion costs. When we profit maximize, we attain a system which produces a Nash equilibrium that is both worse off for the owners of the links, who face lower profits, and for the users of the links, who face higher collective profits, than a monopoly. Simply put, the links do not suffer the full extent of their own pricing policy as they would in the case of a monopoly, where the pricing externality is internalized.
f.o.c.
solving the f.o.c. simultaneously yields:
checking the s.o.c.:
At and , the solution is , which gives , , which is less total profit than the case of the simple monopoly. This situation results in total profit to both firms of 222,222, and a consumer surplus of 55,555, or total social welfare of 277,000, which is less than the results from the case of a simple monopoly. Similar arguments apply to three (or more) perfect complements, which are more and more dysfunctional if operated autonomously. The general formula for N autonomous perfectly complementary links, with linear demand and , is given by:
Case 3. Duopoly of Perfect Substitutes
[edit | edit source]In a third example, we imagine two parallel autonomous links, and , which serve the same, homogenous market. They are perfect substitutes (operate in parallel).
The optimal pricing for this case depends upon assumptions about how users distribute themselves across suppliers and the relationships between the links. First, assume there are no congestion costs and time costs are otherwise equal and not a factor in the decision. Do users simply and deterministically choose the lowest cost link, or are there other factors which shape this choice, so that a minor reduction in price will not attract all users from the other link? For this example, we assume deterministic route choice, so demand chooses the lowest cost link, or splits between the links if they post the same price. Here, demand is defined as below:
As before, let , . Also assume that competitive links can respond instantaneously. Assume each link can serve the entire market, so that there are no capacity restrictions. Clearly there is a (welfare maximizing) stable equilibrium at (assuming equal and zero costs for the links), the result for a competitive system. Demonstration: Suppose each link sets price 500, and had 250 users. If link IJ lowers its prices by one unit to 499, it attains all 501 users, and profits on link IJ increase to 249,999 from 125,000. However profits on link KL drop to 0. The most profitable decision for KL is to lower its price to 498, attain 502 users, and profits of 249,996. This price war can continue until profits are eliminated. At any point in the process raising prices by one link alone loses all demand.
However it seems unlikely in the case of only two links. Therefore, if the links could coordinate their actions they would want to. Even in the absence of formal cartels, strategic gaming and various price signaling methods are possible. For instance, a far sighted link KL, seeing that a price war will ultimately hurt both firms, may only match the price cut rather than undercut in retaliation. If IJ did not follow with a price cut, a price will be maintained. It has been argued (Chamberlin 1933), that the duopoly would act as a monopoly, and both links would charge the monopoly price and split the demand evenly, because that is the best result for each since lowering prices will lead to a price war, with one link either matching or undercutting the other, in both cases resulting in smaller profits.
Case 4. Monopoly and Congestion
[edit | edit source]The previous three cases did not exploit any special features of transportation systems. In this case travel time is introduced on the network used in Case 1. Here demand is a function of both Price () and Time ():
For this example is given by linear form:
where travel time is evaluated with the following expression incorporating both distance effects and congestion (queuing at a bottleneck over a fixed period with steady demand):
if
if
where: = freeflow travel time, = length of congested period, = maximum flow through bottleneck.
Because is a constant, and we are dealing with only a single link, it can be combined with for the analysis and won’t be considered further. By inspection, if is large, it too does not figure into the analysis. From Case 1, with the as given, is only important if it is less than . For this example then, we will set at a value less than 500, in this case assume .
As before, the objective of the link is to maximize profit . Profit is maximized when the first derivative is set to zero and the second derivative is negative.
Giving the following first order conditions (f.o.c.):
Solving equations (4.2) and (4.6) simultaneously, at values: , , reflecting that the value of time for all homogenous travelers is 1 in the chosen unit set, , representing 1800 time units (such as seconds) of congestion, we get the following answer: . It is thus to the advantage of the monopoly in the short term, with capacity fixed, to allow congestion (delay) to continue, rather than raising prices high enough to eliminate it entirely. In the longer term, capacity expansion (which reduces delay), will allow the monopoly to charge a higher price. In this case,, and . There is a large deadweight loss to congestion, as can be seen by comparing with Case 1.
Simulation
[edit | edit source]More complex networks are not easily analyzed in the above fashion. Links serve as complements and substitutes at the same time. Simulation models address the same questions posed in the analytic model on more complex networks, that is, what are the performance measures and market organization under different model parameters and scenarios. Second, we can consider market organization within the model framework, so that the question becomes: What market organization emerges under alternative assumptions, and what are the social welfare consequences of the organization?
Competing links restrict the price that an autonomous link can charge and still maximize profits. Furthermore, it is likely that government regulations will ultimately constrain prices, though the level of regulation may provide great latitude to the owners. It is anticipated that each link will have an objective function for profit maximization. However, depending upon assumptions of whether the firm perfectly knows market demand, and how the firm treats the actions of competitors, the Nash equilibrium solution to the problem may not be unique, or even exist.
Because the demand on a link depends on the price of both upstream and downstream links, its complements, revenue sharing between complementary links, and the concomitant coordination of prices, may better serve all links, increasing their profits as well as increasing social welfare. Vertical integration among highly complementary links is Pareto efficient.
It is widely recognized that the roadway network is subject to economies of density, at least up to a point. This means that as the flow of traffic on a link increases, all else equal, the average cost of operating the link declines. It is less clear if links are subject to economies of scale, that it is cheaper per unit of output (for instance per passenger kilometer traveled) to build and manage two links, a longer link, or a wider link than it is to build and manage a single link, a shorter link, or a narrower link. If there are such economies of scale, then link cost functions should reflect this.
Different classes of users (rich or poor; or cars, buses, or trucks) have different values of time. The amount of time spent on a link depends upon flow on that link, which in turn depends on price. It may thus be a viable strategy for some links to price high and serve fewer customers with a high value of time, and others to price low and serve more customers with a lower value of time. It is hypothesized that in a sufficiently complex network, such distinct pricing strategies should emerge from simple profit maximizing rules and limited amounts of coordination.
There are a number of parameters and rules to be considered in such simulation model, some are listed below.
Parameters
[edit | edit source]Network Size and Shape. The first issue that must be considered is the size of network in terms of the number of links and nodes and how those links connect, determined by the shape of the network (symmetric: grid, radial; asymmetric). While the research will begin with a small network, it is possible that the equilibrium conditions found on limited networks may not emerge on more complex networks, giving cause for considering a more realistic system.
Demand Size and Shape. A second issue is the number of origin-destination markets served by the network, the level of demand, and the number of user classes (each with a different value of time). Again, while the research will begin with very simple assumptions, the results under simple conditions may be very different from those under slightly more complex circumstances.
Rules
[edit | edit source]Profit Seeking. How do autonomous links determine the profit maximizing price in a dynamic situation? Underlying the decision of each autonomous link is an objective function, profit maximization given certain amounts of information, and a behavioral rule which dictates the amount and direction of price changes depending on certain factors. Once a link has found a toll which it can neither raise nor lower without losing profit, it will be tempted to stick with it. However, a more intelligent link may realize that while it may have found a local maxima, because of the non-linearities comprising a complex network, it may not be at a global maxima. Furthermore other links may not be so firmly attached to their decision, and a periodic probing of the market landscape by testing alternative prices is in order. This too requires rules.
Revenue Sharing. It may be advantageous for complementary links to form coalitions to coordinate their action to maximize their profit. How do these coalition form? By the inclusion of a share of the profits of other links in one link’s objective function, that link can price more appropriately. What level of revenue sharing, between 0 and 100 percent is best? These questions need to be tested with the model. An interlink negotiation process will need to be developed.
Cost Sharing. Similar to revenue sharing is the sharing of certain expenses that each link faces. Links face large expenses periodically, such as resurfacing or snow clearance in winter, that have economies of scale. These economies of scale may be realized either through single ownership of a great many links or through the formation of economic networks. Just as revenue sharing between links is a variable which can be negotiated, so is cost sharing.
Rule Evaluation and Propagation. A final set of considerations is the possibility of competition between rules. If we consider the rules to be identified with the firms which own links or shares of links, and set pricing policy, the rules can compete. Accumulated profits can be used by more successful rules to buy shares from less successful rules. The decision to sell will compare future expected profits under current management with the lump sum payment by a competing firm. An open market in the shares of links will need to be modeled to test these issues. Similarly, it may be possible to model rules which learn, and obtain greater intelligence iteration to iteration.
Discussion
[edit | edit source]Just as airline networks seem to have evolved a hub and spoke hierarchy, a specific geometry may be optimal in a private highway network. Initial analysis indicates that there are advantages to both the private and social welfare to vertical integration of highly complementary links. However the degree of complementarity for which integration serves both public and private interests remains to be determined. Other issues that are to be examined include the influence of substitutes and degree of competition on pricing policies through cross-elasticity of demand, economies of scale in the provision of infrastructure, multiple classes of users with different values of time, “free” roads competing with toll roads, and the consequences of regulatory constraints. Using the principles developed under the analytic approach, a repeated game of road pricing by autonomous links learning the behavior of the system through adaptive expectation will be developed.
Additional Problems
[edit | edit source]References
[edit | edit source]- Chamberlin, E (1933) "Monopolistic competition". Harvard University Press
- Coase, Ronald (1992), "The Problem of Social Cost, and Notes on the Problem of Social Cost", reprinted in The Firm, The Market and the Law, Chicago: University of Chicago Press.
- Daganzo, Carlos. (1995). An Informal Introduction To Traffic Flow Theory. University of California at Berkeley, Institute of Transportation Studies. Berkeley, CA.
- Levinson, David and Peter Rafferty (2004) Delayer Pays Principle: Examining Congestion Pricing with Compensation. International Journal of Transport Economics 31:3 295-311
- Vickrey, William (1969) Congestion Theory and Transport Investment. American Economic Review 59, pp. 251–260.




























































