Fluid Mechanics Applications/B18:Impulse Turbines
The word “Turbine” has been derived from the Greek word tyrbē (τύρβη) which has the meaning turbulence. Turbine was invented by Gustaf de Laval in 1882. The modern demonstration of turbine was invented by Sir Charles Parsons in 1884. Turbine is a machine which uses the kinetic energy of fluids and transforms into mechanical energy through a designed mechanism.The turbine consists of several blades which are connected to an axle which is used generally to drives a generator. The basic functioning of the turbine is that the blades of turbine are rotated by the moving fluid(e.g steam, water, gas etc.) which in turn rotates the axle which is connected to a device which uses this rotational energy for the required use.
The turbine is of two types based on the type of its working as follows:

- Impulse turbines: Its blades are rotated by the impulse created the steam on the blades. It consists of blades in form of buckets and nozzles which directs the steam to the curved bucket shaped blades.
- Reaction turbines: its blades are rotated by the torque which is generated by the virtue of fluid’s pressure or mass. It consists of blades of aeroplane wings. Two rows of movable blades are separated by a row of fixed blades attached to the casings acting as nozzles.
Frequently Used Terms
[edit | edit source]- Pressure head: This refers to the potential energy of the fluid under consideration.
- Velocity head: This refers to the kinetic energy of the fluid under consideration.
- Compressible Fluid: Fluid under consideration which have significant density change.
- Incompressible Fluid: Fluid under consideration which don’t have any considerable density change.
IMPULSE TURBINE
[edit | edit source]In impulse turbines, first of all the fluid to be used is directed through a specially designed nozzle to transform its pressure head into velocity head. The required stream of fluid coming out of the nozzle is then impinged on the curved (bucket shaped) blades. The velocity head of this fluid is thus used to provide momentum to rotate the blades and hence the shaft. The blades are designed in such a way that the direction of fluid , from the nozzle, hitting the blades changes its direction and leaves the blade. The impulse generated in this procedure is used to provide the momentum to the blades. This is why we call this type of turbine as impulse turbines.One of the most popular example of impulse turbine is Pelton Wheel
Pelton Wheel
[edit | edit source]Pelton wheel is a type of turbine. It is the most renowned example of Impulse turbine. Lester Allan Pelton invented this water turbine in 1870s. The energy utilised in this turbine is from moving water. Many impulse turbines were made earlier but they were not as efficient the pelton wheel. This was due to the fact that the water leaving the turbines still carried away much of the kinetic energy and hence less energy could be utilised. But Pelton worked on this and found a brilliant solution by giving it paddle geometry. It was designed in such a way that even when the wheel rim had a velocity equal to half of the speed of the water from the nozzle, the water that exited had very less energy left. In this way most of the energy was utilised to the fullest. Making it a very efficient turbine design.
The power required can be varying according to need. So this requirement is met by a spear head mechanism. It is done by adjusting the position of spear head. If power demand is more, then the spear is move towards the exit of nozzle and if power demand is less, the spear head is moved away from the exit of nozzle.So the power demand is synchronised by water flow rate. The nozzle is fitted with a splitter. The special bucket are designed such that the water reverts at . This force can be easily derived from Newton's law The angle is made to be to maximise impulsive force.
To Maximise Power Extraction
Power extracted by Bucket, So the power extracted is maximum when the product of impulsive force and bucket velocity is maximum.
Analysing two situation:
- Buckets are held stationary: There will be a large impulse produced but as the buckets are held stationary so power extracted will be zero.
- Velocity of bucket same as Jet speed : If this happens then the water jet wont be able to hit the bucket leading to zero impulsve force. Thus again no power is extracted.
Mathematical Analysis
[edit | edit source]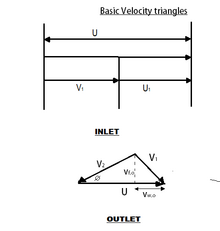
Force exerted by water=
Power=
Hydraulic Efficiency,=
For Maximum Efficiency,
Therefore,
Assuming, frictional resistance along vanes=0
Therefore,
For P to be maximum,
Therefore,
Daugherty's analysis of performance of Pelton Wheel
The net head h supplied to turbine can be found out as follows:
-------(1)
:head converted into mechanical work.
:energy dissipated from heat due to internal friction & eddy losses within runner
:kinetic energy loss at discharge
:loss in nozzle of Pelton wheel

Heat utilised by runner,
-----(2)
Using equation of energy for relative motion of the water in the runner.
The total head loss within the runner
Using relative velocities and equations 1 & 2, we get,
Assume
Tangential Force on bucket,
(Note:In real situation it cannot be assumed that and always jet is striking the bucket at an angle)



























