Algebra/Chapter 4/Compound and Absolute Value Inequalities
Compound Inequalities are two inequalities presented as one problem. The variable being solved for may need to only fulfill only one of the inequalities, or both, depending on if the word "and" or "or" is used. There may be many correct answers, or even none at all.
Example: 2x - 4 > 2 or 30/x > 15
- 2x > 6 or 30 > 15x
- x > 3 or x < 2
The answer can then be graphed as two rays on a number line.
If we are interested in real solutions we can pick numbers barely smaller 2 or hardly greater than 3 as we want and the equation will be true. For instance if x =1.99 then 30/x = 15.08 (satisfies 30/x > 15) or if x = 3.01 then 2x-4 = 2.02 (satisfies 2x -4 > 2).
If we are only interested in integer solutions than we can see that all the integers except for 2 or 3 will work.
We can also express a compound inequality as a function.
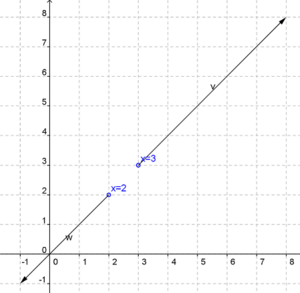
If we specify a function f(x) = (x > 3 or x < 2) we get a graph like this:
The solution is still two rays. But now the rays are on the line y=x, with one ray moving to the right and up from the number 3 and the other moving left and down from the number 2.
Exercise: Using the concept of slope, can you explain why a figure transferred from a number line to a Cartesian graph will always be displayed on the line y=x?
How can I use Compound Inequalities?
[edit | edit source]Example: Highway and City Gas Mileage
[edit | edit source]The gas mileage sticker on cars gives two numbers: one for city driving, and one for highway driving. If a sticker says the car gets 25 mpg in the city and 32 mpg on the highway how far can you drive?
In order to find this out I need to know how much gas I have in my tank. I know that I can drive between 25 and 32 miles with a single gallon of gas. I can represent this with two equations where x = how far I can drive on a gallon of gas:
25 < x and x < 32.
Or I can combine them into a compound inequality:
25 < x < 32.
If I have a 10 gallon gas tank, and I want to know how far I can drive I change the equation to represent the 10 gallons of gas I have in my tank by multiplying each term in the compound inequality by 10.
25 * 10 < 10*x < 32 * 10.
250 < 10x < 320.
I can drive between 250 and 320 miles on a single tank of gas.
Example: Conversions
[edit | edit source]The conversion formula for Fahrenheit to Celsius is 5/9(F - 32).
We know that water freezes at 32 degrees Fahrenheit and boils at 212 degrees Fahrenheit.
If we want to know the freezing point and boiling point of water in Celsius we could set the equation up as follows:
32 < F < 212
And then apply the formula to convert the values in degrees F to degrees C.
5/9(32-32) < C < 5/9(212 - 32)
So water freezes and boils at:
0 < C < 100
Absolute Value
[edit | edit source]What happens when we need to multiply by x?
Remember that subtraction is equivalent to adding a negative number, and multiplication is the same as adding a number multiple times. So when we add a negative number multiple times the result keeps getting smaller. When solving a problem using inequalities we need to decide if the context of the problem makes sense for negative numbers.
A special type of compound inequality involves the absolute value sign. The absolute value sign specifies two functions such that f(x)=A implies f(-x) = (-A)(-1). For the equal sign this is the same as f(x)=f(-x)=A. But when we use an inequality sign and we multiply by a negative number we have to switch the direction of the sign. So if f(x) > A then f(-x) < A.
This is simple when the only the value of x is in the absolute value sign. For instance given|x| > 12 then the possible solutions are x > 12 or x < -12.
| Right side is positive | Right side is zero | Right side is negative |
|---|---|---|
| Gap between 12 and -12. | Any number except 0. | Any number. |
Example - convert |6x + 18| - 33 > 9 into a compound inequality.
- |6x + 18| > 36
- 6x + 18 > 36 or 6x + 18 < -36
- 6x > 18 or 6x < -54
- x > 3 or x < -9
How can you use absolute value?
[edit | edit source]Example 1
A good way to use absolute value is to determine if your previous estimates are right.
For instance, given your car that gets between 25 and 32 miles per gallon. If you want to make sure my car is running well you should keep track of my mileage using the formula:
when m = (miles at last fillup - miles at the pump) and g = amount of fuel I just pumped.
If m/g is not greater than 25 than you should make sure your car is running properly. If m/g is over 32 maybe someone is putting extra gas in your car!
Example 2 - Think like a teacher!
You give five tests in a quarter. A student has made scores of 80 , 90, and a 80 on the first three tests. The student asks you for a chance for extra credit. Should you give the student the chance?
To get a B for the quarter the student needs to make 80*5 = 400. To get an A for the quarter the student needs to get a 450. If we let X equal the student's scores on the last two tests we can see
400 < 250 + x < 450
150 < x < 180
The average score for the last two tests will be x/2. So dividing the equation above by 1/2 we get 75 < x < 90. Since the average score until now is about 83 the student would be encouraged to study harder for the final two tests with just a few extra credit points.