Theory of Computation: Finite state machines
Finite state machines
[edit | edit source]A finite state machine is a form of abstraction (WHY/HOW?). It models the behaviour of a system by showing each state it can be in and the transitions between each state.
Consider an elevator :
Possible states of the system:
'static on floor 1', 'moving up', 'static on floor 2', 'moving down'
[picture of states inserted here]
The transitions and their inputs:
- from 'static on floor 1' to 'moving up' triggered by 'up button'
- from 'moving up' to 'static on floor 2' triggered by 'arrival 2'
- from static on floor 2 to 'moving down' triggered by 'down button'
- from 'moving down' to 'static on floor 1' triggered by 'arrival 1'
Form the above we can draw the finite state machine for the elevator.
[picture of completed finite state machine to be inserted here]
We can also produce a state transition table (DEFINE THIS LANGUAGE BOX?):
[picture of state transition diagram to be inserted here]
Representing a system as a finite state machine is very powerful because the model allows us to demonstrate the behaviour very clearly. We can prove that the system is robust and will not behave in any unexpected manner. Consider the example of the elevator: by modelling the system as a finite state machine, it is possible to show that the elevator is not able to move up and down without stopping. This is because the design clearly shows that it is impossible to transition from the state 'moving up' to the state 'moving down'.
Applications of finite state machines are found in many sciences. Mainly engineering, biology and most commonly in linguistics, where they are used to describe languages.

Looking at the above diagram we can see that it starts in state S1, an input of 1 will keep it in state S1, and an input of 0 will move it to state S2. Once in S2 an input of 1 will keep it there, and an input of 0 will switch it back to S1. This means that the following inputs are valid:
110011001 001110011
It might appear to accept any binary value, but this isn't true. The only state it can accept in is state S1. This places the following rule on all accepted inputs: "A combination of binary digits involving an even number of zeros". This is useful for parity checks. If I try the following:
110011011
I am stuck in state S2 and the FSM has not accepted. Can you create a FSM to only accept Binary numbers with odd numbers of 1s?
|
Exercise: Finite State Automaton Answer:
For the FSM above which of these inputs are valid:
Answer:
Draw a finite state automata that will accept the word Banana whilst using only 3 states Draw a single finite state automata that will accept all the words:
|
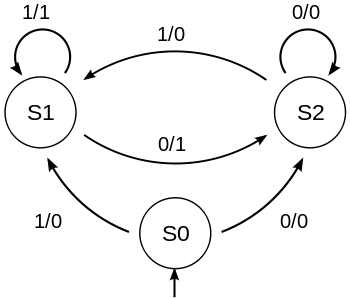
Mealy Machines
[edit | edit source]Some FSMs output values dependent on the state and the input values:

The above Mealy Machine outputs a value for each input. You can tell which is which by: input / ouput. So for the following input:
000101010
It outputs
000010101
Shifting all the bits right, and dividing the binary number input by two.
|
Extension: non-determinism In this section we are learning about deterministic finite automaton. This means that for a state and a valid input there is only one possible transition to take. There are such things a nondeterministic finite automaton where, for a given input there are multiple paths (or none) that could be taken:  |
State transition tables
[edit | edit source]A state transition table follows every state and input. Inputs are usually placed on the left, and separated from the outputs, which are on the right. Here's a simple example of a state machine with two states, and a binary input:
| Input | Current State | Next State | Output |
|---|---|---|---|
| 0 | S1 | S2 | null |
| 1 | S1 | S1 | null |
| 0 | S2 | S1 | null |
| 1 | S2 | S3 | null |
|
Exercise: State transition tables Answer:
Answer:
Draw the FSM for the following state transition table:
Draw the FSM for the following state transition table:
|