Theory of Computation: Maths for regular expressions
Basic set understanding
[edit | edit source]Sets describe collections of things or values, such as numbers, animals or people.
In a set, each value occurs only once. For example, the value fox will occur only once in the set of animals. Just as the value 3 occurs only once in the element of all natural numbers, N.
The cardinality of a set refers to the number of elements it contains.
An empty set is written ∅ and its cardinality is 0.
Sets may be finite or infinite. For example, the set of people currently alive in the world will be finite, but the set of N is infinite.
A set may be countable or uncountable. A countable set is a set, whose elements can be matched with the set of natural numbers. In other words, it is possible to count the elements one-by-one. If a set is finite, it will always be countable. The best example of an uncountable set is R. It is impossible to match each element of R with an element of N. This is because there are not enough elements in N to match each one with an element of R.
Membership ∈ and its reverse ∉
[edit | edit source]x ∈ S, x is an element of S.
Examples:
- x ∈ ℕ, meaning that x is an element of the set of natural numbers. For example, 3 ∈ ℕ. Whereas 3.5 ∉ ℕ
- x ∈ Q, meaning that x is an element of the set of rational numbers. Whereas pi ∉ Q
- x ∈ WorkingDays, meaning that x is an element of the set of all WorkingDays. For example, Monday ∈ WorkingDays. Whereas Saturday ∉ WorkingDays
- x ∈ WeekendDays, meaning that x is an element of the set of all WeekendDays. For example, Saturday ∈ WeekendDays. Whereas Monday ∉ WeekendDays
|
Questions relating to membership and basic understanding Using set notation, state that Sunday is a weekend day. Answer: Sunday ∈ WeekendDays Using set notation, state that Monday is not a weekend day. Answer: Monday ∉ WeekendDays What is the cardinality of the set WeekendDays. Answer: 2 Let set A be the set of all atoms in the world. Which of the following words can be used to describe this set? Countable, uncountable, finite, infinite. Answer: Countable, finite. Let set P be the set of all prime numbers. Which of the following words can be used to describe this set? Countable, uncountable, finite, infinite. Answer: Countable, infinite. |
Union ∪
[edit | edit source]
A ∪ B, meaning that all elements of the set A form a union with all of the elements in set B. This is a set comprehension, since this generates a new set.
Examples:
- Q ∪ Irrational Number Set, meaning that all numbers in the set of rational numbers form a union with the set of all irrational numbers. This set comprehension generates the set of real numbers.
- WorkingDays ∪ WeekendDays, meaning that all of the working days (elements of WorkingDays) form a union with weekend days (elements of WeekendDays). This set comprehension generates the set of WeekDays.
- {1, 2} ∪ {2,3,4} = {1,2,3,4} (notice that only once instance of 2 is in the resulting set)
- {1, 2, green} ∪ {red, white, green}={1, 2, red, white, green}
- {1, 2} ∪ {1, 2} = {1, 2}
|
Questions relating to union Let A = {0,2,4,6,8,10,12} and B = {0,3,6,9,12}. Write out all elements of A ∪ B Answer: {0,2,3,4,6,8,9,10,12}
{3,4} ∪ B
Answer: ={0,3,4,6,9,12}.
A ∪ {7,13,red}
Answer: ={0,2,4,6,7,8,10,12,13,red}.
B ∪ B
Answer: ={0,3,6,9,12}. |
Intersection ∩
[edit | edit source]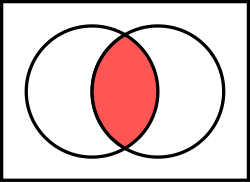
A ∩ B, meaning that the set A and set B form an intersection. The generated set will be ∅, if the two sets share no elements.
Examples:
Let A be the set of numbers which are divisible by 3 and B the set of numbers divisible by 4.
- A ∩ B, meaning that A and B form an intersection, which generates a set, which contains all of the numbers divisible by 3 and 4.
- WorkingDays ∩ WeekendDays, meaning that WorkingDays and WeekendDays form an intersection, which is ∅
Now let A be the set of all A-level students who take computer science and B the set of all A-level students who take mathematics.
- A ∩ B, meaning that A and B form an intersection, which generates a set, which contains all students who take both computer science and mathematics.
- {1, 2, 3} ∩ {2, 3, 4} = {2, 3}
- {1, 2, 3} ∩ {bear,hen,squirrel} = Ø (this means an empty set)
- {cat, dog, canary} ∩ {wolf, canary, whale, cat} = {cat, canary}
|
Questions relating to intersection As above, let A = {0,2,4,6,8,10,12} and B = {0,3,6,9,12}.
Answer: {0,6,12}
A ∩ {goat,4,6,9} =
Answer: {4,6}
A ∩ {goat,3,9} =
Answer: It has no intersected values (Ø)
B ∩ {3,5,7,9,11} =
Answer: {3,9} |
Difference \
[edit | edit source]A \ B, meaning that the set A and set B form a set difference. This will generate a set, which contains the elements of A, which are NOT also in B.

Examples:
- R \ Q, meaning that R and Q form a set difference. This will generate the set of irrational numbers.
Let A be the set of all A-level students who take computer science and B the set of all A-level students who take mathematics.
- A \ B, meaning that A and B form a set difference. This will generate the set of all computer science students, who do not also take mathematics.
- {1, 2, 3} ∩ {2, 3, 4} = {2, 3}
- {1, 2, 3} ∩ {bear,hen,squirrel} = Ø (this means an empty set)
- {cat, dog, canary} ∩ {wolf, canary, whale, cat} = {cat, canary}
|
Questions relating to difference As above, let A = {0,2,4,6,8,10,12} and B = {0,3,6,9,12}. Let us take a look at the two sets we are using as examples: A ∖ B =Answer: {2,4,8,10}
B ∖ A =
Answer: {3,9}
B ∖ {1,2,3,5,7,11} =
Answer: {0,6,9,12}
A ∖ {0,1,2,3,5,8,13} =
Answer: {4,6,10,12} |
Proper Subsets ⊂
[edit | edit source]S ⊂ T, meaning that S is a proper subset of T, such that all elements in S are also elements of T. However, there will need to be at least one element in T, which is not in S.
Examples:
- N ⊂ Z, meaning that the set of natural numbers is a proper subset of the set of integers. In other words, all natural numbers are also integers. There are some elements in Z, which are not in N - these are the negative integers.
- Z ⊂ Q, meaning that the set of integers is a proper subset of the set of rational numbers. In other words, all integers are also rational numbers. But there are rational numbers which are not integers.
|
Questions relating to proper subsets As above, let A = {0,2,4,6,8,10,12} and B = {0,3,6,9,12}. Is A a proper subset of B, so that we can write A ⊂ B? Explain your answer. Answer: No, because there are elements in the set A which are not in the set B. In other words we can find an element, for which x ∈ A and x ∉ B Relating to the above definitions for A, define a set which is a proper subset of A. Answer: Any valid answer, for example {0,2,12} or {8,12} |
Subsets ⊆
[edit | edit source]A ⊆ B, meaning that A forms a subset of B. In other words, A could be identical to B, but does not have to be!
Examples:
Let A be the set of all students in 6th form and B the set of all students taking computer science.
- A ⊆ B, meaning that A forms a subset of B. In other words, all students in the 6th form could be taking computer science. In which case the two sets would be the same, but they may not be!
Now let A be all of the students present in school and B the set of students currently in the assembly hall.
- A ⊆ B, meaning that A forms a subset of B. In other words, all students currently in present in school may all be located in the assembly hall, but they may not be!
|
Questions relating to subsets Let A be all students who sit the A-level exam in computer science. Let B be all the students who gain a 'B' grade or above in the A-level computer science exam. Is B a subset of A? Explain your answer. Answer: Yes, because it may be the case that all students who sit the exam will also gain grade 'B' or above. Let A be the set of customers in a restaurant. Let B be the set of all the vegetarian customers in the restaurant. Is B a subset of A? Could A be a subset of B? Could A be a proper subset of B? Explain your answer. Answer: B is a subset of A since every vegetarian customer is a customer. A could be a subset of B, because it may be the case that all customers present are also vegetarian. It cannot be a proper subset, since A contains B. |


