Semiconductors/Doping
When examining crystals we make a few assumptions about them for simplicity. Such as:
- They are Periodic
- They are symmetrical
- They are infinitely large
- They compose a lattice
Although the infinite claim is a bit sketchy, it is a pretty good approximation as these crystals are often huge compared to distances in the crystal.
Since crystals exist in 3D space, and are periodic, if we move the size of the crystal in one of its axis we are at a corresponding spot. Mathematically we say that we have three linearly independent vectors and can move integer values of them to corresponding places in the lattice.
Unit Cells[edit | edit source]
If we have a lattice it must be made up of smaller components, the unit cell is the smallest undivisible part of the lattice. And by placing many unit cells together, you can create the whole lattice again. Imagine a large stack of dice, you could say that one die was the unit cell for this crystalline lattice.
There is an infinite number of possible unit cells, but only 14 types of lattice. This can be generalised to 7 crystal classes.
Also there is a minimum size of the unit cell, with its volume being 1 lattice point (atom/molecule/whatever).
Some Cells and their Packing Fractions[edit | edit source]
Cubic[edit | edit source]
Imagine a cubic unit cell with one point at each corner. So 8 points in total, but each of these is shared between it and 7 other cubes.
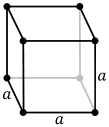
So the amount of lattice points per cell is 8 * 1/8 = 1. We call this the Primitive.
Now if we imagine each point as a sphere which touches its neighbours, then we can define the Packing Fraction as the volume taken up by the points compared to the volume of the cell.
In Cubic cells each sphere will have a radius half the size of the crystal. So we say r = a/2.
And there is one per cell, ie the primitive = 1. So:
or 52%
Body Centre Cubic[edit | edit source]
Like a cubic unit cell except has another lattice point directly in its centre.
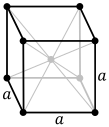
Primitive = 8 * 1/8 + 1 = 2.
It has a Packing Fraction of 68%.
Face Centre Cubic[edit | edit source]
This is a close packed lattice, it's like a cubic except all 6 faces have another point at their centre.

Primitive = 8 * 1/8 + 6 * 1/2 = 4
Packing Fraction = 74%


