Introduction to Inorganic Chemistry/Metals and Alloys: Structure, Bonding, Electronic and Magnetic Properties
Chapter 6: Metals and Alloys: Structure, Bonding, Electronic and Magnetic Properties[edit | edit source]

In the chemistry of molecular compounds, we are accustomed to the idea that properties depend strongly on structure. For example we can rationalize the polarity of the water molecule based on its shape. We also know that two molecules with the same composition (e.g., ethanol and dimethyl ether) have very different properties based on the bonding arrangements of atoms. It should come as no surprise that the properties of extended solids are also connected to their structures, and so to understand what they do we should begin with their crystal structures. Most of the metals in the periodic table have relatively simple structures and so this is a good place to begin. We will see in Chapter 8 that the structures of more complex compounds are also in many cases related to the simple structures of metals and alloys.
Learning goals for Chapter 6:
- Identify and assign unit cells, coordination numbers, asymmetric units, numbers of atoms contained within a unit cell, and the fraction of space filled in a given structure.
- Relate molecular orbital theory to the delocalization of valence electrons in metals.
- Understand the concepts of electron wavelength and density of states.
- Understand the consequences of the nearly free electron model for the band structure of metals and their conductivity.
- Explain why some metals are magnetic and others are diamagnetic, and how these phenomena relate to bonding and orbital overlap.
- Use the Curie-Weiss law to explain the temperature dependence of magnetic ordering.
- Acquire a physical picture of different kinds of magnetic ordering and the magnetic hysteresis loops of ferro- and ferrimagnets.
6.1 Unit cells and crystal structures[edit | edit source]

Crystals can be thought of as repeating patterns, much like wallpaper or bathroom tiles, but in three dimensions. The fundamental repeating unit of the crystal is called the unit cell. It is a three dimensional shape that can be repeated over and over by unit translations to fill space (and leave no gaps) in the structure. Some possible unit cells are shown in the tiling pattern at the right, along with arrows that indicate unit translation vectors. In three dimensions, the hexagonal or rhombic unit cells of this pattern would be replaced by three dimensional boxes that would stack together to fill all space. As shown in the figure, the origin of the unit cell is arbitrary. The same set of boxes will fill all space no matter where we define the origin of the lattice. We will see that pure metals typically have very simple crystal structures with cubic or hexagonal unit cells. However the crystal structures of alloys can be quite complicated.
When considering the crystal structures of metals and alloys, it is not sufficient to think of each atom and its neighboring ligands as an isolated system. Instead, think of the entire metallic crystal as a network of atoms connected by a sea of shared valence electrons. The electrons are delocalized because there are not enough of them to fill each "bond" between atoms with an electron pair. For example, in the crystal structures of s-block and p-block metals, each atom has either 8 or 12 nearest neighbors, but the maximum number of s + p electrons is 8. Thus, there are not enough to put two electrons between each pair of atoms. Transition metals can also use their d-orbitals in bonding, but again there are never enough electrons to completely fill all the "bonds."
The atoms in a metal lattice arrange themselves in a certain pattern which can be represented as a 3D box structure known as the unit cell which repeats across the entire metal.
| Simple Cubic | Body Centered Cubic | Face Centered Cubic | Hexagonal Close Packed |
|---|---|---|---|

|

|

|

|
| 1 atom/cell | 2 atoms/cell | 4 atoms/cell | 2 atoms/cell |


Metal atoms can be approximated as spheres, and therefore are not 100 % efficient in packing, the same way a stack of cannonballs has some empty spaces between the balls. Different unit cells have different packing efficiencies. The number of atoms that is included in the unit cell only includes the fractions of atoms inside of the box. Atoms on the corners of the unit cell count as ⅛ of an atom, atoms on a face count as ½, an atom in the center counts as a full atom. Using this, let's calculate the number of atoms in a simple cubic unit cell, a face centered cubic (fcc) unit cell, and a body centered cubic (bcc) unit cell.
Simple Cubic:
8 corner atoms × ⅛ = 1 atom/cell. The packing in this structure is not efficient (52%) and so this structure type is very rare for metals.
Body Centered Cubic, bcc:
(8 corner atoms × ⅛) + (1 center atom × 1)= 2 atoms/cell. The packing is more efficient (68%) and the structure is a common one for alkali metals and early transition metals. Alloys such as brass (CuZn) also adopt these structures.
Face Centered Cubic, fcc (also called Cubic Close Packed, ccp):
(8 corner atoms × ⅛)+ (6 face atoms × ½)= 4 atoms/cell. This structure, along with its hexagonal relative (hcp), has the most efficient packing (74%). Many metals adopt either the fcc or hcp structure.
Hexagonal Close Packed, hcp:
Like the fcc structure, the packing density of hcp is 74%.
Calculating the packing fraction. The packing fractions of the crystal structures shown above can be calculated by dividing the volume of the atoms in the cell by the volume of the cell itself. The volume of the atoms in the cell is equal to the number of atoms/cell times the volume of a sphere, (4/3)πr3. The volume of the cubic cells is found by cubing the side length. As an example, let's calculate the packing efficiency of a simple cubic unit cell. As we saw earlier in the section, a simple cubic unit cell contains one atom. The side length of the simple cubic unit cell is 2r, since the centers of each atom occupy the corners of the unit cell.
Packing efficiency=[(1 atom)×(4/3)πr3]/[(2r)3]=0.523
The same method can be applied to bcc and fcc structures.
6.2 Bravais lattices[edit | edit source]
Crystal lattices can be classified by their translational and rotational symmetry. In three-dimensional crystals, these symmetry operations yield 14 distinct lattice types which are called Bravais lattices. In these lattice diagrams (shown below) the dots represent lattice points, which are places where the whole structure repeats by translation. For example, in the body-centered cubic (bcc) structure of sodium metal, which is discussed below, we put one atom at the corner lattice points and another in the center of the unit cell. In the NaCl structure, which is discussed in Chapter 8, we place one NaCl formula unit on each lattice point in the face-centered cubic (fcc) lattice. That is, one atom (Na or Cl) would be placed on the lattice point and the other one would be placed halfway between. Similarly, in the cubic diamond structure, we place one C2 unit around each lattice point in the fcc lattice.
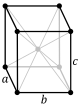
The fourteen Bravais lattices fall into seven crystal systems that are defined by their rotational symmetry. In the lowest symmetry system (triclinic), there is no rotational symmetry. This results in a unit cell in which none of the edges are constrained to have equal lengths, and none of the angles are 90º. In the monoclinic system, there is one two-fold rotation axis (by convention, the b-axis), which constrains two of the angles to be 90º. In the orthorhombic system, there are three mutually perpendicular two-fold axes along the three unit cell directions. Orthorhombic unit cells have three unequal unit cell edges that are mutually perpendicular. Tetragonal unit cells have a four-fold rotation axis which constrains all the angles to be 90º and makes the a and b axes equivalent. The rhombohedral system has a three-fold axis, which constrains all the unit cell edges and angles to be equal, and the hexagonal system has a six-fold axis, which constrains the a and b lattice dimensions to be equal and the angle between them to be 120º. The cubic system has a three-fold axis along the body diagonal of the cube, as well as two-fold axes along the three perpendicular unit cell directions. In the cubic system, all unit cell edges are equal and the angles between them are 90º.
The translational symmetry of the Bravais lattices (the lattice centerings) are classified as follows:
- Primitive (P): lattice points on the cell corners only (sometimes called simple)
- Body-Centered (I): lattice points on the cell corners with one additional point at the center of the cell
- Face-Centered (F): lattice points on the cell corners with one additional point at the center of each of the faces of the cell
- Base-Centered (A, B, or C): lattice points on the cell corners with one additional point at the center of each face of one pair of parallel faces of the cell (sometimes called end-centered)
Not all combinations of the crystal systems and lattice centerings are unique. There are in total 7 × 6 = 42 combinations, but it can be shown that several of these are in fact equivalent to each other. For example, the monoclinic I lattice can be described by a monoclinic C lattice by different choice of crystal axes. Similarly, all A- or B-centred lattices can be described either by a C- or P-centering. This reduces the number of combinations to 14 conventional Bravais lattices, shown in the table below.
When the fourteen Bravais lattices are combined with the 32 crystallographic point groups, we obtain the 230 space groups. These space groups describe all the combinations of symmetry operations that can exist in unit cells in three dimensions. For two-dimensional lattices there are only 17 possible plane groups, which are also known as wallpaper groups.
| Crystal family | Lattice system | Schönflies | 14 Bravais Lattices | |||
|---|---|---|---|---|---|---|
| Primitive | Base-centered | Body-centered | Face-centered | |||
| Triclinic | Ci | 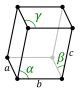
|
||||
| Monoclinic | C2h | 
|

|
|||
| Orthorhombic | D2h | 
|

|
|

| |
| Tetragonal | D4h | 
|

|
|||
| Hexagonal | rhombohedral | D3d | 
|
|||
| hexagonal | D6h | 
|
||||
| Cubic | Oh | 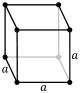
|

|

| ||
6.3 Crystal structures of metals[edit | edit source]



The Crystalline Nature of Metals. All metallic elements (except Cs, Ga, and Hg) are crystalline solids at room temperature. Like ionic solids, metals and alloys have a very strong tendency to crystallize, whether they are made by thermal processing or by other techniques such as solution reduction or electroplating. Metals crystallize readily and it is difficult to form a glassy metal even with very rapid cooling. Molten metals have low viscosity, and the identical (essentially spherical) atoms can pack into a crystal very easily. Glassy metals can be made, however, by rapidly cooling alloys, particularly if the constituent atoms have different sizes. The different atoms cannot pack in a simple unit cell, sometimes making crystallization slow enough to form a glass.
Crystal structures. Most metals and alloys crystallize in one of three very common structures: body-centered cubic (bcc), hexagonal close packed (hcp), or cubic close packed (ccp, also called face centered cubic, fcc). In all three structures the coordination number of the metal atoms (i.e., the number of equidistant nearest neighbors) is rather high: 8 for bcc, and 12 for hcp and ccp. We can contrast this with the low coordination numbers (i.e., low valences - like 2 for O, 3 for N, or 4 for C) found in nonmetals. In the bcc structure, the nearest neighbors are at the corners of a cube surrounding the metal atom in the center. In the hcp and ccp structures, the atoms pack like stacked cannonballs or billiard balls, in layers with a six-coordinate arrangement. Each atom also has six more nearest neighbors from layers above and below. The stacking sequence is ABCABC... in the ccp lattice and ABAB... in hcp. In both cases, it can be shown that the spheres fill 74% of the volume of the lattice. This is the highest volume fraction that can be filled with a lattice of equal spheres.

Atoms in metallic crystals have a tendency to pack in dense arrangements that fill space efficiently. The simple square packing (left) upon which the simple cubic structure is based is inefficient and thus rare among metallic crystal structures. Body- or face-centered structures fill space more efficiently and more common.


Periodic trends in structure and metallic behavior. Remember where we find the metallic elements in the periodic table - everywhere except the upper right corner. This means that as we go down a group in the p-block (let's say, group IVA, the carbon group, or group VA, the nitrogen group), the properties of the elements gradually change from nonmetals to metalloids to metals. The carbon group nicely illustrates the transition. Starting at the top, the element carbon has two stable allotropes - graphite and diamond. In each one, the valence of carbon atoms is exactly satisfied by making four electron pair bonds to neighboring atoms. In graphite, each carbon has three nearest neighbors, and so there are two single bonds and one double bond. In diamond, there are four nearest neighbors situated at the vertices of a tetrahedron, and so there is a single bond to each one.
The two elements right under carbon (silicon and germanium) in the periodic table also have the diamond structure (recall that these elements cannot make double bonds to themselves easily, so there is no graphite allotrope for Si or Ge). While diamond is a good insulator, both silicon and germanium are semiconductors (i.e., metalloids). Mechanically, they are hard like diamond. Like carbon, each atom of Si and Ge satisfies its valence of four by making single bonds to four nearest neighbors.
The next element under germanium is tin (Sn). Tin has two allotropes, one with the diamond structure, and one with a slightly distorted bcc structure. The latter has metallic properties (metallic luster, malleability), and conductivity about 109 times higher than Si. Finally, lead (Pb), the element under Sn, has the ccp structure, and also is metallic. Note the trends in coordination number and conducting properties:
| Element | Structure | Coord. no. | Conductivity |
|---|---|---|---|
| C | graphite, diamond | 3, 4 | semimetal, insulator |
| Si | diamond | 4 | semiconductor |
| Ge | diamond | 4 | semiconductor |
| Sn | diamond, distorted bcc | 4, 8 | semiconductor, metal |
| Pb | ccp | 12 | metal |
The elements C, Si, and Ge obey the octet rule, and we can easily identify the electron pair bonds in their structures. Sn and Pb, on the other hand, adopt structures with high coordination numbers. They do not have enough valence electrons to make electron pair bonds to each neighbor (this is a common feature of metals). What happens in this case is that the valence electrons become "smeared out" or delocalized over all the atoms in the crystal. It is best to think of the bonding in metals as a crystalline arrangement of positively charged cores with a "sea" of shared valence electrons gluing the structure together. Because the electrons are not localized in any particular bond between atoms, they can move in an electric field, which is why metals conduct electricity well. Another way to describe the bonding in metals is nondirectional. That is, an atom's nearest neighbors surround it in every direction, rather than in a few particular directions (like at the corners of a tetrahedron, as we found for diamond). Nonmetals (insulators and semiconductors), on the other hand, have directional bonding. Because the bonding is non-directional and coordination numbers are high, it is relatively easy to deform the coordination sphere (i.e., break or stretch bonds) than it is in the case of a nonmetal. This is why elements like Pb are much more malleable than C, Si, or Ge.
6.4 Bonding in metals[edit | edit source]


The electron pair description of chemical bonds, which was the basis of the octet rule for p-block compounds, breaks down for metals. This is illustrated well by Na metal, the structure of which is shown at the left. Na has too few valence electrons to make electron pair bonds between each pair of atoms. We could think of the Na unit cell as having eight no-bond resonance structures in which only one Na-Na bond per cell contains a pair of electrons.
A more realistic way to describe the bonding in metals is through band theory. The evolution of energy bands in solids from simple MO theory (Chapter 2) is illustrated at the right for a chain of six Na atoms, each of which has one 3s valence orbital and contributes one valence electron. In general, n atomic orbitals (in this case the six Na 3s orbitals) will generate n molecular orbitals with n-1 possible nodes. In Chapter 2, we showed that the energy versus internuclear distance graph for a two hydrogen atom system has a low energy level and a high energy level corresponding to the bonding and antibonding molecular orbitals, respectively. These two energy levels were well separated from each other, and the two electrons in H2 energetically prefer the lower energy level. If more atoms are introduced to the system, there will be a number of additional levels between the lowest and highest energy levels.

In band theory, the atom chain is extrapolated to a very large number - on the order of 1022 atoms in a crystal - so that the different combinations of bonding and anti-bonding orbitals create "bands" of possible energy states for the metal. In the language of physics, this approach of building the bands from discrete atomic orbitals is called the "tight-binding" approximation. The number of atoms is so large that the energies can be thought of as a continuum rather than a series of distinct levels. A metal will only partially fill this band, as there are fewer valence electrons than there are energy states to fill. In the case of Na metal, this results in a half-filled 3s band.
Nearly free electron model. In metals, the valence electrons are delocalized over many atoms. The total energy of each electron is given by the sum of its kinetic and potential energy:
- E = KE + PE
- E ≈ p2/2m + V
where p is the momentum of the electron (a vector quantity), m is its mass, and V is an average potential that the electron feels from the positive cores of the atoms. This potential holds the valence electrons in the crystal but, in the free electron model, is essentially uniform across the crystal.

Electron wavelength and wavenumber. What are the consequences of this model for band theory? For a hypothetical infinite chain (i.e., a 1D crystal) of Na atoms, the molecular orbitals at the bottom of the 3s band are fully bonding and the wavelength of electrons (2x the distance between nodes) in these orbitals is very long. At the top of the band, the highest orbital is fully antibonding and the wavelength is 2 times the distance between atoms (2a), since there is one node per atom. Remember that the wavelength of an electron (λ) is inversely proportional to its momentum p, according to the de Broglie relation λ = h/p.
For a (nearly) free electron, the kinetic energy can be expressed in terms of its wavelength, using KE = p2/2m and the de Broglie relation:
- KE = p2/2m = h2/(2mλ2)
At this point, it is convenient to define the wavenumber of the electron as k, which has units of inverse length and is inversely proportional to λ. k is also directly proportional to the momentum p. Like p, k is a vector quantity. In a 1D crystal, k can be either positive or negative, corresponding to an electron moving to the left or right along the chain.
- k = 2π/λ = 2πp/h, where h is Planck's constant
The most important property of k is that it is directly proportional to the number of nodes n in a molecular orbital within the band. For a 1D crystal of sodium atoms that contains N unit cells, each separated by a distance a, a molecular orbital with n nodes has a wavelength λ = 2Na/n and the wavenumber k = πn/Na. We can see from this definition that k = 0 at the bottom of the band (where λ is infinite) and k = π/a at the top of the band where the MO contains N nodes and λ = 2a.
Energies of orbitals in a metallic crystal. Electrons with long wavelengths do not "feel" the individual atoms in the lattice and so they behave as if they are nearly free (but confined to the crystal). Near the bottom of the band, the electron energy increases parabolically with the number of nodes (KE ∝ n2), since the momentum p is directly proportional to n. Because p is also directly proportional to k, we can write:
- KE = p2/2m = h2k2/8π2m
This parabolic relationship is followed as long as the electron wavelength is long compared to the distance between atoms. Near the top of the band, the wavelength becomes shorter and the electrons start to feel the positively charged atomic cores. In particular, the electrons prefer to have the maxima in their wavefunctions line up with the atomic cores, which is the most electrostatically favorable situation. The electron-atom attraction lowers the energy and causes the E vs. k curve to deviate from the parabolic behavior of a "free" electron as shown in the figure below.





Density of States (DOS). The density of states is defined as the number of orbitals per unit of energy within a band. Because of the parabolic relation between E and k, the density of states for a 1D metallic crystal is highest near the bottom and top of the energy band where the slope of the E vs. k curve is closest to zero. The shape of the DOS curve is different in crystals of higher dimensionality as shown in the figure in the left, because statistically there are more ways to make an orbital with N/2 nodes than there are with zero or N nodes. The situation is analogous to the numbers you can make by rolling dice. With one die, the numbers 1-6 have equal probability. However, with two dice there is only one way to make a two (snake eyes) or a twelve (boxcars), but many ways to make a seven (a winner!).
While most of the time we will talk about 3D crystals that have their maximum DOS near the middle of the energy band, there are examples of quasi-1D systems, such as carbon nanotubes. Metallic carbon nanotubes have strong optical absorption bands that correspond to transitions between the two regions of high DOS (the van Hove singularities) near the bottom and top of the bands.
Metals, semiconductors, and insulators. The degree to which bands fill determines whether a crystalline solid is a metal, semiconductor, or insulator. If the highest occupied molecular orbitals lie within a band - i.e., if the Fermi level EF cuts through a band of orbitals - then the electrons are free to change their speed and direction in an electric field and the solid is metallic. However, if the solid contains just enough electrons to completely fill a band, and the next highest set of molecular orbitals is empty, then it is a semiconductor or insulator. In this case, there is an energy gap between the filled and empty bands, which are called the valence and conduction bands, respectively. Although the distinction is somewhat arbitrary, materials with a large gap (> 3 eV) are called insulators, and those with smaller gaps are called semiconductors. We will learn more about the properties of semiconductors in Chapter 10.

Why don't insulators conduct electricity? The energy vs. DOS diagram to the right shows what happens when an electric field is applied to a metal or an insulator. In this case we have changed the diagram to show explicitly the energies of electrons moving left and right. These energies are the same in the absence of an electric field. Once we apply a field (e.g., by putting a voltage across a metal wire), the electrons moving in the direction of the field have lower energy than those moving in the opposite direction. In the case of the metal, the populations of electrons moving with and against the electric field are different, and there is a net flow of current. Note that this can happen only when the Fermi level cuts through a partially filled band. With a semiconductor or insulator, the valence band is filled and the conduction band is empty. Applying an electric field changes the energies of electrons traveling with and against the field, but because the band is filled, the same number are going in both directions and there is no net current flow.
Note that in this picture, all the molecular orbitals extend over the entire crystal. The valence electrons are delocalized, even in the case of a semiconductor or insulator. However, there can be no net movement of electrons unless the band is partially filled.
6.5 Conduction in metals[edit | edit source]

In metals, the valence electrons are in molecular orbitals that extend over the entire crystal lattice. As we will learn in Chapter 7, metals are almost always crystalline and the individual crystal grains are typically micron size. This means that the spatial extent of the orbitals is very large compared to the size of the atoms or the unit cell. The diagram at the left shows a generic plot of electron energy vs. density of states for a metal such as Na, Cu, or Ag. In these cases, there are N orbitals for N electrons, and each orbital can accommodate two electrons. Therefore the Fermi level, which corresponds to the energy of the highest occupied MO at zero temperature, is somewhere in the middle of the band of orbitals. The energy level spacing between orbitals is very small compared to the thermal energy kT, so we can think of the orbitals as forming a continuous band.
Classically, if the electrons in this band were free to be thermally excited, we would expect them to have a specific heat of 3 R per mole of electrons. However, experimentally we observe that Cp is only about 0.02 R per mole. This suggests that only about 1% of the electrons in the metal can be thermally excited at room temperature. However, essentially all of the valence electrons are free to move in the crystal and contribute to electrical conduction. To understand this apparent paradox, we need to recall that the electrons exist in quantized energy levels.
Because of quantization, electrons in metals have a Fermi-Dirac distribution of energies. In this distribution, most of the electrons are spin-paired, although the individual electrons in these pairs can be quite far apart since the orbitals extend over the entire crystal. A relatively small number of electrons at the top of the Fermi sea are unpaired by thermal excitation. This is the origin of the Pauli paramagnetism of metals.
How fast are electrons traveling in a typical metal? Because of the bell shape of the E vs. DOS curve, most of the electrons have E ≈ EF. At the midpoint energy (EF) of the band, the MO's have one node for every two atoms. We can calculate the de Broglie wavelength as twice the distance between nodes and thus:
- λ = 4a at the midpoint of the band.
where a is the interatomic spacing. Since a typical value of a is about 2 Å, we obtain the de Broglie wavelength λ ≈ 8 Å.
Using the de Broglie relation p = h/λ, we can write:
- p = h/λ = mevF,
where me is the mass of the electron and vF is the velocity of electrons with energy EF.
Solving for vF = h/meλ we obtain vF = (6.62 x 10-34 J s)/(9.1 x 10-31 kg)(8 x 10-10 m) = 1.0 x 106 m/s, which is about 1/300 the speed of light. This is the Fermi velocity.
Experimental values of vF are 1.07 x 106 and 1.39 x 106 m/s for Na and Ag, respectively, confirming the above estimate.
However, the drift velocity of electrons in metals - the average speed at which electrons move in applied electric field - is quite slow, on the order of 0.0001 m/s, or .01 cm/s.

In order to understand the great disparity between the Fermi velocity and the drift velocity of electrons in metals, we need to consider a picture for the scattering of electrons, and their acceleration in an electric field, as shown at the left. If we apply a voltage across a metal (e.g., a metal wire), the electrons are subjected to an electric field E, which is the voltage divided by the length of the wire. This electric field exerts a force on the electron, causing it to accelerate. However, the electron is frequently scattered, mostly by phonons (lattice vibrations). Each time the electron is scattered its acceleration starts all over again. The time between scattering events is τ and the distance the electrons travel between scattering events is the mean free path, λ. (Note that this is NOT the same λ as the de Broglie wavelength, they just are being denoted by the same symbol.)
We can write the force on the electron as:
- F = eE = mea = mevdrift/τ

In this equation, a is the acceleration in the electric field, me is the mass, and vdrift is the drift velocity of the electron.
Experimentally, the mean free path is typically obtained by measuring the scattering time. For an electron in Cu metal at 300 K, the scattering time τ is about 2 x 10-14 s. From this we can calculate the mean free path as:
- λ = vavgτ ≈ vFτ = (1 x 106 m/s)(2 x 10-14 s) = 40 nm
The mean free path (40 nm = 400 Å) is quite long compared to the interatomic spacing (2 Å). To put it in perspective, if the interatomic spacing were scaled to the length of a football (0.3 m), the mean free path would be over half the length of the football field (60 m). Thus an electron travels a fairly long way between scattering events and scarcely notices the atomic structure of the metal in which it is traveling.
To summarize, electrons are traveling in metals at the Fermi velocity vF, which is very, very fast (106 m/s), but the flux of electrons is the same in all directions. That is, they are going nowhere fast. In an electric field, a very small but directional drift velocity is superimposed on this fast random motion of valence electrons.
We can calculate the drift velocity of electrons as the acceleration in the electric field times the scattering time:
From F = ma, we obtain the acceleration (a) as:
- a = F/me = eE/me
And thus,
- vdrift = aτ = eEτ/me
If we divide both sides of this equation by the magnitude of the electric field (E), we obtain the mobility (μ):
- μ = vdrift/E = eτ/me
μ has units of velocity/field = cm/s / V/cm = cm2/Vs
An important consequence of the calculation of vdrift is Ohm's Law, V = iR. From the equations above, we can see that the drift velocity increases linearly with the applied electric field. The drift velocity (cm/s) is proportional to the current (i, coul/s), and the electric field (E, V/cm) is proportional to the voltage (V):
- Current (i) = n e vdrift x area
- Voltage (V) = E x length
Here n is the density of valence electrons (#/cm3) and e is the charge of the electron (coul). Combining these equations with our equation for vdrift we obtain:
Thus, V = iR, where R is the combination of the two terms in parentheses. The first of these is the resistivity, , and the second is a geometrical factor.
The conductivity (σ) of a metal, which is the inverse of , is proportional to μ, which in turn is proportional to τ (and λ):
- σ = neμ = ne2τ/me
We can use this equation to work out the conductivity of a specific metal (Cu), for which n = 8.5 x 1022 cm-3 and τ = 2 x 10-14 s. Putting in the numbers for me and e, we obtain σ = 7 x 105 Ω-1 cm-1 for Cu, in good agreement with the measured value (6 x 105 Ω-1cm-1).
6.6 Atomic orbitals and magnetism[edit | edit source]


The MO picture we developed in Section 6.4 helps us rationalize the electrical conductivity of Na (3s1), but what about Mg, which (as an atom in the gas phase) has a 3s2 electronic configuration? The two valence electrons are spin-paired in atomic Mg, as they are in the helium atom (1s2). When the 3s orbitals of Mg combine to form a band, we would expect the band to be completely filled, since Mg has two electrons per orbital. By this reasoning, solid Mg should be an insulator. But Mg has all the properties of a metal: high electrical and thermal conductivity, metallic luster, malleability, etc. In this case the 3s and 3p bands are sufficiently broad (because of strong orbital overlap between Mg atoms) that they form a continuous band. This band, which contains a total of four orbitals (one 3s and three 3p) per atom, is only partially filled by the two valence electrons.
Another way to think about this is to consider the hybridization of the 3s and 3p electrons in Mg. Hybridization requires promotion from the 3s23p0 ground state of an Mg atom to a 3s13p1 excited state. The promotion energy (+264 kJ/mol) is more than offset by the bonding energy (-410 kJ/mol), the energy released when gaseous atoms in the excited state condense to form the metallic solid. The heat of vaporization, or the cohesive energy of a metal, is the difference between the bonding energy and the promotion energy. Experimentally, we can measure the vaporization energy (+146 kJ/mol) and the promotion energy and use them to calculate the bonding energy. From this we learn that each s or p electron is worth about 200 kJ/mol in bonding energy. The concepts of promotion energy and bonding energy are very useful in rationalizing periodic trends in the bond strengths and magnetic properties of metals, which are described below.

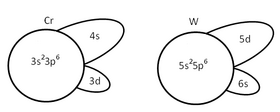
Periodic trends in d-electron bonding. While electrons in s and p orbitals tend to form strong bonds, d-electron bonds can be strong or weak. There are two important periodic trends that are related to orbital size and orbital overlap. As we move across the periodic table ( Sc - Ti - V - Cr - Fe ), the d orbitals contract because of increasing nuclear charge. Moving down the periodic table ( V - Nb - Ta ), the d orbitals expand because of the increase in principal quantum number. These trends explain the distinct behavior of the 3d elements relative to those in the 4d and 5d series. In the 3d series, the contraction of orbitals affects the ability of the d electrons to contribute to bonding. Past V in the first row of the transition metals, the 3d electrons become much less effective in bonding because they overlap weakly with their neighbors. Weak overlap of 3d orbitals gives narrow d-bands and results in the emergence of magnetic properties as discussed below.

In the 4d and 5d series, a plot of cohesive energy vs. number of valence electrons (below left) has a "volcano" shape that is peaked at the elements Mo and W (5s14d5 and 6s15d5, respectively). The number of bonding electrons, and therefore the bonding energy, increases steadily going from Rb to Mo in the 4d series, and from Cs to W in the 5d series. Mo and W have the most bonding energy because they can use all six of their valence electrons in bonding without promotion. Elements past Mo and W have more d electrons, but some of them are spin paired and so some promotion energy is needed to prepare these electrons for bonding. For example, Pt metal must be promoted from the 6s15d9 atomic ground state to 6s15d76p2 in order to make six bonds per atom, and the energy cost of promoting electrons from the 5d to the 6p orbitals is reflected in the net bonding energy. Because of their strong bonding energy, elements in the middle of the 4d and 5d series have very high melting points. We do not see magnetism in the 4d or 5d metals or their alloys because orbital overlap is strong and the bonding energy exceeds the electron pairing energy.

The 3d elements (Sc through Zn) are distinctly different from the 4d and 5d elements in their bonding (and consequently in their magnetic properties). In the 3d series, we see the expected increase in cohesive energy going from Ca (4s2) to Sc (4s23d1) to Ti (4s23d2) to V (4s23d3), but then something very odd happens. The 3d series has a "crater" in the cohesive energy plot where there was a peak in the 5d series. The cohesive energy actually decreases going from V to Mn, even though the number of valence electrons is increasing. We can explain this effect by remembering that the 3d orbitals are progressively contracting as more protons are added to the nucleus. For elements beyond V, the orbital overlap is so poor that the 3d electrons are no longer effective in bonding, and the valence electrons begin to unpair. At this point the elements become magnetic. Depending on the way the spins order, metals and alloys in this part of the periodic table can be ferromagnetic (spins on neighboring atoms aligned parallel, as in the case of Fe or Ni) or antiferromagnetic (spins on neighboring atoms antiparallel, as in the case of Mn).
We have seen the trade-off between orbital overlap and magnetism before (in Chapter 5) in the context of paramagnetic transition metal complexes. It is worth recalling that this behavior is predicted in the energy vs. distance diagram of the hydrogen atom (from Chapter 2). At short interatomic distances (or with strong overlap between atomic orbitals), the spins of the electrons pair and a bond is formed. Unpairing the electrons becomes favorable at larger interatomic distances where the overlap between orbitals is poor.
Interestingly, many alloys of the 4f elements (the lanthanides) are also magnetic because the 4f orbitals, like the 3d orbitals, are poorly shielded from the nuclear charge and are ineffective in bonding. Strong permanent magnets often contain alloys of Nd, Sm, or Y, usually with magnetic 3d elements such as Fe and Co.
Because the 4f orbitals are contracted and not very effective in bonding, other physical properties of the lanthanides can also be affected. For example, it has been proposed that oxides of the 4f elements have weak surface interactions with polar molecules such as water because of f-orbital contraction. Experimentally, CeO2, Er2O3, and Ho2O3 are observed to be hydrophobic, whereas main group and early transition metal oxides (e.g., Al2O3, SiO2, TiO2) are quite hydrophilic.[1]
Late transition metal alloys. Although the bonding in the 5d series follows a "normal" volcano plot, the situation is a bit more complex for alloys of Re, Os, Ir, Pt, and Au. There is strong overlap between the 5d orbitals, but because these elements contain more than five d-electrons per atom, they cannot make as many bonds as 4d or 5d elements with half-filled d-shells such as Mo or W. This progressive filling of the d-band explains the steady decrease in bonding energy going from Os to Au. Pt and Au are both soft metals with relatively low heats of vaporization. However, these metals (especially Ir, Pt, and Au) can combine with early transition metals to form stable alloys with very negative heats of formation and high melting points. For example, ZrC and Pt react to form a number of stable alloys (ZrPt, Zr9Pt11, Zr3Pt4, ZrPt3)[2] plus carbon. This reactivity is unusual because we normally think of Pt as a "noble" (i.e., unreactive) metal, and because ZrC is a very stable, refractory metal carbide. The favorable combination of early and late transition metals has been interpreted as arising from a d-electron "acid-base" interaction.[3] For example, in HfPt3, Hf is the "acid" with an electron configuration of 6s25d2, while Pt is the "base" with the electron configuration of 6s15d9. They combine to create a stable "salt" product with a filled 5d electron configuration without promoting any electrons to higher orbitals. The implication is that Pt donates d-electrons to the "d-acid," Zr or Hf. However, electronic structure calculations on model compounds show that much of the bonding energy in ZrPt and ZrPt3 arises from electron transfer from Zr to Pt (not the other way around) and the polarity of the resulting metal-metal bonds.[4] Regardless of the source of their stability, some early-late transition metal alloys are of particular interest for use in catalysis. For example, the alloy ScPt3 is a good catalyst for oxygen reduction in fuel cells. Even though Sc is an active metal that is easily oxidized, it is stabilized in the aqueous acid environment of the fuel cell by its strong interaction with Pt.[5]

Filling of the 3d and 4s,4p bands. In the 3d series, we see magnetic behavior for elements and alloys between Cr and Ni. Past Ni, the elements (Cu, Zn, Ga,...) are no longer magnetic and they are very good electrical conductors, implying that their valence electrons are highly delocalized. We can understand this behavior by considering the overlap of 4s, 4p, and 3d orbitals, all of which are close in energy. The 4s and 4p have strong overlap and form a broad, continuous band. On the other hand, the 3d electrons are contracted and form a relatively narrow band. Progressing from the early 3d elements (Sc, Ti, V), we begin to fill the 3d orbitals, which are not yet so contracted that they cannot contribute to bonding. Thus, the valence electrons in Sc, Ti, and V are all spin-paired, except for a small number near the Fermi level that give rise to a weak Pauli paramagnetism. Moving across the 3d series to the magnetic elements (Fe, Co, Ni), the d-orbitals are now so contracted that their electrons unpair and we see cooperative ordering of spins (ferromagnetism and antiferromagnetism). Referring to the band diagram at the right, the 3d band is only partially filled and the Fermi level cuts through it. For Cu, Zn, and Ga, the 3d orbitals are even more contracted and the 3d band is thus more narrow, but now it is completely filled and the Fermi level is in the 4s,4p band. The strong orbital overlap in these bands results in spin pairing and a high degree of electron delocalization. Consequently, metals in this part of the periodic table (Cu, Ag) are diamagnetic and are among the best electrical conductors at room temperature. Finally, at Ge, the 4s,4p band is completely filled and the solid is a semiconductor.
Materials are classified as diamagnetic if they contain no unpaired electrons. Diamagnetic substances are very weakly repelled from an inhomogeneous magnetic field. As we learned in Chapter 5, molecules or ions that have unpaired spins are paramagnetic and are attracted to a magnet, i.e., they move towards the high field region of an inhomogeneous field. This attractive force results from the alignment of spins with the field, but in the case of paramagnetism each molecule acts independently. In metals, alloys, oxides, and other solid state compounds, the unpaired spins interact strongly with each other and can order spontaneously, resulting in the cooperative magnetic phenomena described below.
6.7 Ferro-, ferri- and antiferromagnetism[edit | edit source]
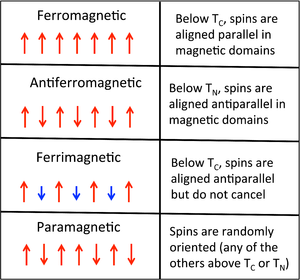
The magnetism of metals and other materials are determined by the orbital and spin motions of the unpaired electrons and the way in which unpaired electrons align with each other. All magnetic substances are paramagnetic at sufficiently high temperature, where the thermal energy (kT) exceeds the interaction energy between spins on neighboring atoms. Below a certain critical temperature, spins can adopt different kinds of ordered arrangements.
Let's begin by considering an individual atom in the bcc structure of iron metal. Fe is in group VIIIb of the periodic table, so it has eight valence electrons. The atom is promoted to the 4s13d7 state in order to make bonds. A localized picture of the d-electrons for an individual iron atom might look like this:
Since each unpaired electron has a spin moment of 1/2, the total spin angular momentum, S, for this atom is:
- S = 3(1/2) = 3/2 (in units of h/2π)
We can think of each Fe atom in the solid as a little bar magnet with a spin-only moment S of 3/2. The spin moments of neigboring atoms can align in parallel (↑ ↑), antiparallel (↑ ↓), or random fashion. In bcc Fe, the tendency is to align parallel because of the positive sign of the exchange interaction. This results in ferromagnetic ordering, in which all the spins within a magnetic domain (typically hundreds of unit cells in width) have the same orientation, as shown in the figure at the right. Conversely, a negative exchange interaction between neighboring atoms in bcc Cr results in antiferromagnetic ordering. A third arrangement, ferrimagnetic ordering, results from an antiparallel alignment of spins on neighboring atoms when the magnetic moments of the neighbors are unequal. In this case, the spin moments do not cancel and there is a net magnetization. The ordering mechanism is like that of an antiferromagnetic solid, but the magnetic properties resemble those of a ferromagnet. Ferrimagnetic ordering is most common in metal oxides, as we will learn in Chapter 7.
Magnetization and susceptibility. The magnetic susceptibility, χ, of a solid depends on the ordering of spins. Paramagnetic, ferromagnetic, antiferromagnetic, and ferrimagnetic solids all have χ > 0, but the magnitude of their susceptibility varies with the kind of ordering and with temperature. We will see these kinds of magnetic ordering primarily among the 3d and 4f elements and their alloys and compounds. For example, Fe, Co, Ni, Nd2Fe14B, SmCo5, and YCo5 are all ferromagnets, Cr and MnO are antiferromagnets, and Fe3O4 and CoFe2O4 are ferrimagnets. Diamagnetic compounds have a weak negative susceptibility (χ < 0).
Definitions
- H = applied magnetic field (units: Henry (H))
- B = induced magnetic field in a material (units: Tesla (T))
- M = magnetization, which represents the magnetic moments within a material in the presence of an external field H.
- Magnetic susceptibility χ = M/H
Usually, χ is given in molar units in the cgs system:
- χM = molar susceptibility (units: cm3/mol)
Typical values of χM:
To correlate χ with the number of unpaired electrons in a compound, we first correct for the small diamagnetic contribution of the core electrons:

- χcorr = χobs - χdiamagnetic cores
Susceptibility of paramagnets. For a paramagnetic substance,
The inverse relationship between the magnetic susceptibility and T, the absolute temperature, is called Curie's Law, and the proportionality constant C is the Curie constant:
Note that C is not a "constant" in the usual sense, because it depends on µeff, the effective magnetic moment of the molecule or ion, which in turn depends on its number of unpaired electrons:
Here µB is the Bohr magneton, a physical constant defined as µB = eh/4πme = 9.274 x 10-21 erg/gauss (in cgs units).
In cgs units, we can combine physical constants,
Combining these equations, we obtain

These equations relate the molar susceptibility, a bulk quantity that can be measured with a magnetometer, to µeff, a quantity that can be calculated from the number of unpaired electrons, n. Two important points to note about this formula are:
- The magnetic susceptibility is inversely proportional to the absolute temperature, with a proportionality constant C (Curie's Law)
- So far we are talking only about paramagnetic substances, where there is no interaction between neighboring atoms.
Returning to the isolated Fe atom with its three unpaired electrons, we can measure the Curie constant for iron metal (above the temperature of its transition to a paramagnetic solid) and compare it to the calculation of µeff. Since n = 3, we calculate:
The plot at the right shows the number of unpaired electrons per atom, calculated from measured Curie constants, for the magnetic elements and 1:1 alloys in the 3d series. The plot peaks at a value of 2.4 spins per atom, slightly lower than we calculated for an isolated iron atom. This reflects that fact that there is some pairing of d-electrons, i.e., that they do contribute somewhat to bonding in this part of the periodic table.
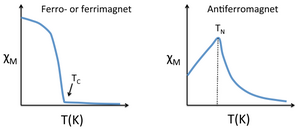

Susceptibility of ferro-, ferri-, and antiferromagnets. Below a certain critical temperature, the spins of a solid paramagnetic substance order and the susceptibility deviates from simple Curie-law behavior. Because the ordering depends on the short-range exchange interaction, this critical temperature varies widely. Metals and alloys in the 3d series tend to have high critical temperatures because the atoms are directly bonded to each other and the interaction is strong. For example, Fe and Co have critical temperatures (also called the Curie temperature, Tc, for ferromagnetic substances) of 1043 and 1400 K, respectively. The Curie temperature is determined by the strength of the magnetic exchange interaction and by the number of unpaired electrons per atom. The number of unpaired electrons peaks between Fe and Co as the d-band is filled, and the exchange interaction is stronger for Co than for Fe. In contrast to ferromagnetic metals and alloys, paramagnetic salts of transition metal ions typically have critical temperatures below 1K because the magnetic ions are not directly bonded to each other and thus their spins are very weakly coupled in the solid state. For example, in gadolinium sulfate, the paramagnetic Gd3+ ions are isolated from each other by SO42- ions.
Above the critical temperature TC, ferromagnetic compounds become paramagnetic and obey the Curie-Weiss law:
This is similar to the Curie law, except that the plot of 1/χ vs. T is shifted to a positive intercept TC on the temperature axis. This reflects the fact that ferromagnetic materials (in their paramagnetic state) have a greater tendency for their spins to align in a magnetic field than an ordinary paramagnet in which the spins do not interact with each other. Ferrimagnets follow the same kind of ordering behavior. Typical plots of χ vs. T and 1/χ vs. T for ferro-/ferrimagnets are shown at the right.
Antiferromagnetic solids are also paramagnetic above a critical temperature, which is called the Néel temperature, TN. For antiferromagnets, χ reaches a maximum at TN and is smaller at higher temperature (where the paramagnetic spins are further disordered by thermal energy) and at lower temperature (where the spins pair up). Typically, antiferromagnets retain some positive susceptibility even at very low temperature because of canting of their paired spins. However the maximum value of χ is much lower for an antiferromagnet than it is for a ferro- or ferrimagnet. The Curie-Weiss law is also modified for an antiferromagnet, reflecting the tendency of spins (in the paramagnetic state above TN) to resist parallel ordering. A plot of 1/χ vs. T intercepts the temperature axis at a negative temperature, -θ, and the Curie-Weiss law becomes:


Ordering of spins below TC. Below TC, the spins align spontaneously in ferro- and ferrimagnets. Complex magnetization behavior is observed that depends on the history of the sample. For example, if a ferromagnetic material is cooled in the absence of an applied magnetic field, it forms a mosaic structure of magnetic domains that each have internally aligned spins. However, neighboring domains tend to align the opposite way in order to minimize the total energy of the system. This is illustrated in the figure at the left for a Nd-Fe-B magnet. The sample consists of 5-10 µm wide crystal grains that can be easily distinguished by the sharp boundaries in the image. Within each grain are a series of lighter and darker stripes (imaged by using the optical Kerr effect) that are ferromagnetic domains with opposite orientations. Averaged over the whole sample, these domains have random orientation so the net magnetization is zero.
When a sample like this one is magnetized (i.e., exposed to a strong magnetic field), the domain walls move and the favorably aligned domains grow at the expense of those with the opposite orientation. This transformation can be seen in real time in the Kerr microscope. The domain walls are typically hundreds of atoms wide, so movement of a domain wall involves a cooperative tilting of spin orientation (analogous to "the wave" in a sports stadium) and is a relatively low energy process.


The process of magnetization moves the solid away from its lowest energy state (random domain orientation), so magnetization involves input of energy. When the external magnetic field is removed, the domain walls relax somewhat, but the solid (especially in the case of a "hard" magnet) can retain much of its magnetization. If you have ever magnetized a nail or a paper clip by using a permanent magnet, what you were doing was moving the walls of the magnetic domains inside the ferromagnet. The object thereafter retains the "memory" of its magnetization. However, annealing a permanent magnet destroys the magnetization by returning the system to its lowest energy state in which all the magnetic domains cancel each other.
Magnetic hysteresis. Hysteresis is the dependence of the state of a system on its history. For example, a magnet may have more than one possible magnetic moment in a given magnetic field, depending on how the field changed in the past. Plots of a single component of the moment often form a loop or hysteresis curve, where there are different values of one variable depending on the direction of change of another variable. This history dependence is the basis of memory in a hard disk drive and the remanence that retains a record of the Earth's magnetic field magnitude in the past. Hysteresis occurs in ferromagnetic and ferroelectric materials, as well as in the deformation of rubber bands and shape-memory alloys and many other natural phenomena.
Cycling a ferro- or ferrimagnetic material in a magnetic field results in hysteresis in the magnetization of the material, as shown in the figure above. At the beginning, the magnetization is zero, but it begins to rise rapidly as the magnetic field is applied. At high field, the magnetic domains are aligned and the magnetization is said to be saturated. When the field is removed, a certain remanent magnetization (indicated as the point Br on the graph) is retained, i.e., the material is magnetized. Applying a field in the opposite direction begins to orient the magnetic domains in the other direction, and at a field Hc (the coercive field), the magnetization of the sample is reduced to zero. Eventually the material reaches saturation in the opposite direction, and when the field is removed again, it has remanent magnetization Br, but in the opposite direction. As the field continues to reverse, the magnet follows the hysteresis loop as indicated by the arrows. The area of colored region inside the loop is proportional to the magnetic work done in each cycle. When the field cycles rapidly (for example, in the core of a transformer, or in read-write cycles of a magnetic disk) this work is turned into heat.
6.8 Hard and soft magnets[edit | edit source]

Whether a ferro- or ferrimagnetic material is a hard or a soft magnet depends on the strength of the magnetic field needed to align the magnetic domains. This property is characterized by Hc, the coercivity. Hard magnets have a high coercivity (Hc), and thus retain their magnetization in the absence of an applied field, whereas soft magnets have low values.
The figure at the right compares hysteresis loops for hard and soft magnets. Recall that the energy dissipated in magnetizing and demagnetizing the material is proportional to the area of the hysteresis loop. We can see that soft magnets, while they can achieve a high value of Bsat, dissipate relatively little energy in the loop. This makes soft magnets preferable for use in transformer cores, where the field is switched rapidly. Permalloy, an alloy consisting of about 20% Fe and 80% Ni, is a soft magnet that has very high magnetic permeability µ (i.e., a large maximum slope of the B vs. H curve) and a very narrow hysteresis loop.
Some materials, such as iron metal, can exist as either hard or soft magnets. Whether bcc iron is a hard or soft magnet depends on the crystal grain size. When crystal grains in iron are sub-micron size, and comparable to the size of the magnetic domains, then the magnetic domains are pinned by crystal grain boundaries. When the magnetic domains are pinned a stronger coercive magnetic field needs to be applied to cause them to re-align. When iron is annealed, the crystal grains grow and the magnetic domains become more free to align with applied magnetic fields. This decreases the coercive field and the material becomes a soft magnet.
Hard magnets such as CrO2, γ-Fe2O3, and cobalt ferrite (CoFe2O4) are used in magnetic recording media, where the high coercivity allows them to retain the magnetization state (read as a logical 0 or 1) of a magnetic bit over long periods of time. Hard magnets are also used in disk drives, refrigerator magnets, electric motors and other applications. Drive motors for hybrid and electric vehicles such as the Toyota Prius use the hard magnet Nd2Fe14B (also used to make strong refrigerator magnets) and require 1 kilogram (2.2 pounds) of neodymium.[6]. A high-resolution transmission electron microscope image of Nd2Fe14B is shown below and compared to the crystal structure with the unit cell marked.

6.9 Discussion questions[edit | edit source]
- Discuss the relationship between the trends in bonding energy of the transition metals and their magnetic properties.
- Draw the hcp unit cell in sections and show how you would calculate (a) the number of atoms in the unit cell and (b) the fraction of space filled by equal spheres.
6.10 Problems[edit | edit source]
1. C-centered (base-centered) Bravais lattices exist in the monoclinic and orthorhombic systems but not in the tetragonal system. That is because the C-centered tetragonal lattice is equivalent to one of the other Bravais lattices. Which one is it? Show with a drawing how that lattice is related to the C-centered tetragonal lattice. How many atoms are in the unit cell of that lattice?
2. Which of the following sequences of close-packed layers fills space most efficiently? Explain your answer.
(a) ABACCABA...
(b) ABABAB...
(c) AABBAABB...
(d) ABACABAC...
3. Calculate the fraction of space that is occupied by packing spheres in the (a) simple cubic, (b) body-centered cubic structure, (c) face-centered cubic (cubic close packed) structures. Assume that nearest neighbor spheres are in contact with each other.

4. The hexagonal close packed (hcp) structure is shown at the right. If the radius of the spheres is R, what is the vertical distance between layers in units of R? What fraction of space is filled by the spheres in the hcp lattice?
5. Consider a one-dimensional chain of sodium atoms that contains N atoms, where N is a large number. The distance between atoms in the chain is the lattice constant a. In the highest occupied molecular orbital of the chain, what is the distance between nodes (in units of a)?
6. Starting from the left side of the periodic table, the melting and boiling points of the elements first increase, and then decrease. For example, the order of boiling points is Rb < Sr < Y < Zr < Nb < Mo > Tc ≈ Ru > Rh > Pd > Ag. Briefly explain the reason for this trend.
7. Going across the periodic table from left to right starting from potassium, the bonding energies and heats of vaporization increase in the order K < Ca < Sc < Ti < V, but then decrease going from V to Mn (V > Cr > Mn). The heats of vaporization of V, Cr, and Mn are much less than those of Nb, Mo, and Tc, respectively. Explain these trends.
8. Some alloys of early and late transition metals (e.g., ZrPt3) have much higher enthalpies of vaporization (per metal atom) than either pure metal. Why are such alloys unusually stable, relative to the pure metals?
9. Graphite is a semimetal composed of sheets of fused benzene rings. There are no bonds between sheets, only van der Waals interactions. What is the C-C bond order in graphite? Show why the C-C distance (1.42 Å) is different from that of benzene (1.40 Å).
10. Fe, Co, and Ni are ferromagnetic, whereas Ru, Ir, and Pt are diamagnetic. Explain why magnetic metals are found only among the 3d and 4f elements. Why are Sc and Ti, which are also 3d elements, diamagnetic?
11. The Curie temperature of cobalt is 1127•C, which is higher than that of Fe (770•C) or Ni (358•C). Why does Co have the highest Curie temperature?
12. Iron metal comes in magnetically “soft” and “hard” forms. Briefly explain the structural differences between them and draw magnetic hysteresis curves for each, indicating on your curves the coercive field and the remanent magnetization.
13. Aluminum metal has the fcc structure, a lattice constant of 4.046 Å, three valence electrons per atom, and an electron scattering time (at room temperature) of 11.8 fs. Use these values to calculate the room temperature resistivity (in ohm-cm) of Al metal.
6.11 References[edit | edit source]
- ↑ G. Azimi et al., Nature Materials 12,315–320 (2013), doi:10.1038/nmat3545
- ↑ Stalick, J. K.; Waterstrat, R. J. J. Alloys Compounds 430, 123-131 (2007).
- ↑ Brewer, L.; Wengert, P. R. Metall. Trans. 1973, 4, 83.
- ↑ Wang, H.; Carter, E. A.; J. Am. Chem. Soc. 1993, 115, 2357-2362.
- ↑ Greeley, J. et al., Alloys of platinum and early transition metals as oxygen reduction electrocatalysts, Nature Chem. 1, 552 - 556 (2009)
- ↑ MotorTrend, Jan. 6, 2021












