Fermat's Last Theorem/Appendix
This appendix collects some proofs and studies in depth some mathematical concepts that can be interesting in order to examine in depth some aspects of the book. It seeks to maintain a simple approach but the proofs being correct, in some cases however it was necessary to make recourse to some non immediate concepts and passages that have been specified and clarified where possible.
Pythagoras’ theorem[edit | edit source]
Being one of the most noted theorems in the history of mathematics, many proofs exist, the work of astronomers, stockbrokers, and even one by Leonardo da Vinci. Probably, together with quadratic reciprocity, it contends for the prize for the theorem with the most absolute proofs. It will be proved in a graphical manner utilising only the concepts of elementary geometry. Pythagoras’ proof will not be quoted being very complex and not immediate.
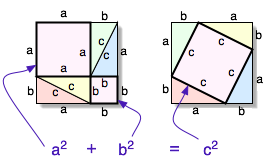
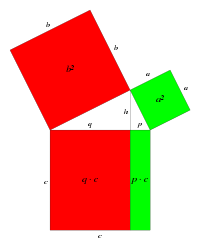
The proof is very simple, as one sees from the graphic one constructs first a square formed by four triangles and by two squares, one of side a and the second of side b. The area of a square is calculated multiplying the side by itself or in modern notation the area is the side raised to the power two. The area of the large square is therefore the sum of the areas of the squares values a2 and b2 plus the sum of the four triangles. In the second square we have again four triangles and a square of area c2. The four triangles being present both to the left of the equality and to the right can be eliminated. Therefore remaining in the equation:
As one wished to prove. It is to be noted that the proof is generic and effectively covers every possible right angled triangle given that numbers are not utilised in the proof but only generic segments length a, b and c. The proof depends solely on the fact that the triangles are right angled and on the fact that one is utilising Euclidean geometry. This is a small gallery of some geometrical proofs of the theorem even if as was said above there are very many proofs and in fact there are also purely algebraic proofs, proofs that utilise complex numbers and even proofs written in the form of sonnets.
Fundamental theory of arithmetic[edit | edit source]
The fundamental theory of arithmetic states that every natural number that is not 1 admits one and only one factorisation in prime numbers not taking account of the order of the factors. (The exclusion of 1 is due to the fact that it does not have prime factors.) This theorem was the basis of the proofs of Gabriel Lamé and Augustin Luis Cauchy and as was said in general is not valid for complex numbers therefore it cannot be utilised for Fermat’s theorem but given its importance it was decided however to include the proof in the appendix. The statement is easily verifiable for “small” natural numbers: it is easy to discover that 70 is equal to 2 × 5 × 7 while 100 equates to 2 × 2 × 5 × 5 or 22 × 52, and furthermore it is easy to verify that for these numbers other decompositions into prime factors cannot exist. Conversely the general proof is rather longer: Here is an extract of it. It deals with a proof for absurd: that is it starts from the hypothesis contrary to that of the statement in order to be able to prove it unfounded.
One supposes that there exist some number reducible into prime factors in more than one way, and one calls the smallest m. Firstly one proves that, given two factorisations of m, the prime numbers that present themselves in the first factorisation are all distinct from those in the second factorisation. They are in fact two different factorisations:
[1]
[2]
where pi and qj are prime. (Note: within a single factorisation there can be repeated factors, naturally: for example, 100 = 2 × 2 × 5 × 5). Were there to be an identical factor ph = qk, we could divide m by such a factor and obtain a number m' , less than m, that would also itself have two distinct factorisations. At this point we know that p1 is different from q1; without loss of generality we can suppose that p1 < q1. We put then
[3]
Evidently, n < m, given that [3] can be written as:
[4]
- .
We now demonstrate that n admits at least two distinct factorisations. We begin by considering if the first factor of n, q1 - p1, can or cannot be prime; in the case that it was not, we suppose factorising it. The factorisation of n thus obtained does not admit p1 among its factors. In fact, from the first part of the proof, we know that p1 is different from q2, q3, ..., qt; but it cannot none the less appear in the eventual factorisation of q1 - p1. If in fact it happened that would mean that
and therefore q1 would be divisible by p1, which is not possible in as much as q1 is a prime number. Taking now the final equality [4] and substituting for m the value from [1], we obtain:
[5]
In whatever way the second factor in [5], may be factorised, we will have obtained a factorisation of n that contains p1, and that therefore is different from that in [3], contrary to the hypothesis that m was the smallest number that admitted more than one factorisation. The theorem is therefore proved.
Principle of Induction[edit | edit source]
The Principle of induction states that
If is a subset of the set of natural numbers that satisfy the following two properties:
- contains ,
- every time that contains a number contains also the successive number ,
then coincides with all of the set of natural numbers
This is found in general within the axioms of Peano and furnishes a potent instrument for proofs in all sectors of mathematics. In the book it is recalled at times given that many mathematicians have sought to prove a base case of Fermat's theorem and then of generalising the solution in order to be able include therein the successive cases by means of this principle.
Proof by induction[edit | edit source]
In order to prove that a certain assertion in which appears a natural number valid for whatever one must apply the principle of induction in the following way:
One puts ,
- one proves as valid, that is that is in the set of natural numbers for which is valid;
- one assumes as a hypothesis that the assertion may be valid for a generic and from such an assumption one also proves that (that is that )
and therefore one concludes that the set of numbers for which is valid is valid coincides with all the set of natural numbers. Point 1 is generally called base of the induction, point 2 the inductive step.
The following is an intuitive mode in which one can look at this type of proof: if we have available a proof of the base of the inductive step then clearly we can make use of these proofs in order to prove using the logical rule modus ponens on (the base) and (which is a particular case of the inductive step for ), then we can prove since now we are using the modus ponens on and , thus for , , etcetera... it is clear at this point that we can produce a proof in a finite number of steps (eventually very lengthy) of for whatever natural number , from which we deduce that is true for every .
An example[edit | edit source]
We will prove that the following formula is valid:
- For every :
In this case we have .
- Base base of the induction: we have to prove the assertion is true for , and so, substituting, that , and in effect there is very little work, one is talking of an elementary calculation;
- Inductive step: we must show that for every n the implication is valid, that is, substituting:
Therefore we must assume as true
- ,
working on this equality and concluding with the analogous equality for : We could for example add to both sides of the equality P(n):
- ,
then we make some simple algebraic steps:
- ,
- ,
and this final equality is exactly . This concludes the proof of the inductive step.
Having therefore proved the base of the induction and the inductive step we can conclude (from the principle of induction) that must be true for every .
Modular Arithmetic[edit | edit source]
Modular arithmetic (sometimes called clock arithmetic since the calculation of the hours in cycles of 12 or 24 is based on such principle) represents an important branch of mathematics. It finds applications in cryptography, in the theory of numbers (in particular in the research of prime numbers), and it is the basis of many of the most common arithmetical and algebraic operations. It deals with a system of integer arithmetic, in which the numbers "wrap round on themselves " every time that they reach multiples of a specific number n, called the modulo. Modular arithmetic was formally introduced by Carl Friedrich Gauss in his treatise Disquisitiones Arithmeticae, published in 1801. Modular arithmetic is based on the concept of congruence modulo n . Given three whole numbers a, b, n, with n≠0, we say that a and b are congruent modulo n if their difference (a−b) is a multiple of n. In this case we write
and we say that a is congruent to b modulo n. For example, we can write
since 38 − 14 = 24, which is a multiple of 12. In the case that both numbers are positive, one can also say that a and b are congruent modulo n if they have the same remainder from division by n. Therefore we can also say that 38 is congruent 14 modulo 12 since both 38 and 14 have remainder 2 after division by 12.
Properties of congruence[edit | edit source]
Congruence is a relationship of equivalence between integer numbers as one sees from the following properties:
- Reflexive property: every number is congruent to itself modulo n, for every n different from fixed 0.
- Proof: one has a - a = 0. But as is noted, every non-zero integer is a divisor of 0. Therefore n divides (a - a)
- Symmetrical property: if a is congruent to b modulo n then b is congruent to a modulo n
- Proof: if n divides (a - b), then n also divides the opposite (b - a) = - (a - b
- Transitive property: if a is congruent to b modulo n and b is congruent to c modulo n then also a is congruent to c modulo n.
- Proof: if n divides (a - b) and n divides (a - c) then, because of the distributive property of the division with respect to the subtraction, n also divides [(a - c) - (a - b)]=[a - c - a + b] = (b - c).
Invariance with respect to arithmetical operations[edit | edit source]
Another important characteristic of the relationship of congruence is the fact of being preserved by the usual arithmetical operations between integers:
- Invariance by addition: increasing or reducing two numbers congruent modulo n by the same quantity, the new numbers obtained are still congruent between themselves modulo n. More synthetically
- Proof: we write (a - b) = (a - b + c - c) = (a + c) - (b + c)
- Invariance by multiplication: multiplying two numbers congruent modulo n by the same quantity, the new numbers obtained are still congruent between themselves modulo n.
- Proof: if n divides (a - b) then n divides (a - b)×c
- Note: One can only invert this property if n does not divide c, that is if c is not congruent to 0 (modulo n).
- Invariance with respect to raising to a power: raising two numbers congruent modulo n to the same power k, the numbers obtained are still congruent between themselves modulo n.
- Proof: if a ≡ b ≡ 0 (mod n) the proposition is banal. If a ≡ b (mod n) is non null, we suppose to know that . Multiplying both the terms by a thanks to invariance by multiplication, we will have . We start now from the congruence a ≡ b (mod n) and we multiply both the members by , thanks always to invariance by multiplication. We obtain:. Comparing the two expressions, and utilising the symmetrical and transitive properties, one deduces that . Since the proposition is true for k = 1 and the fact that it may be true for k-1 implies that it is true for k, by the principle of induction the proposition is true for every k.
- Note: This property can be inverted only if k is not 0.