Electronics/Latches and Flip Flops
Intro
[edit | edit source]A flip-flop is a circuit which exists in one of two states and so can store information.
A simple flip-flop can be defined in terms of two NAND logic gates. Flip-flops are non linear circuits, meaning the output from one of its gates is fed 'back' to be processed with the input signal. Because flip-flops operate on an input signal mixed with this previous output signal their own outputs are dependent upon their previous state.
A flip flop (F/F) is a device made out of digital gates that uses feedback to store the state (1 or 0) of its input(s). Flip Flops are frequently used to latch input data. Meaning that in a circuit they are fed some binary value and then hold it until the latch is turned off. All flip flops have at least one output labeled Q. Frequently they have a complement, labeled /Q. The 4 basic flip flops are SR, D, Toggle and JK.
A latch is an example of a bistable multivibrator, that is, a device with exactly two stable states. These states are high-output and low-output. A latch has a feedback path, so information can be retained by the device. Therefore latches can be memory devices, and can store one bit of data for as long as the device is powered. As the name suggests, latches are used to "latch onto" information and hold in place. Latches are very similar to flip-flops, but are not synchronous devices, and do not operate on clock edges as flip-flops do.
SR latch
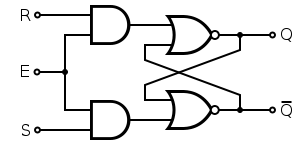
[edit | edit source]An SR latch (Set/Reset) is an asynchronous device: it works independently of control signals and relies only on the state of the S and R inputs. In the image we can see that an SR flip-flop can be created with two NOR gates that have a cross-feedback loop. SR latches can also be made from NAND gates, but the inputs are swapped and negated. In this case, it is sometimes called an SR latch.
When a high is applied to the Set line of an SR latch, the Q output goes high (and Q low). The feedback mechanism, however, means that the Q output will remain high, even when the S input goes low again. This is how the latch serves as a memory device. Conversely, a high input on the Reset line will drive the Q output low (and Q high), effectively resetting the latch's "memory". When both inputs are low, the latch "latches" – it remains in its previously set or reset state.
When both inputs are high at once, however, there is a problem: it is being told to simultaneously produce a high Q and a low Q. This produces a "race condition" within the circuit – whichever flip flop succeeds in changing first will feedback to the other and assert itself. Ideally, both gates are identical and this is "metastable", and the device will be in an undefined state for an indefinite period. In real life, due to manufacturing methods, one gate will always win, but it's impossible to tell which it will be for a particular device from an assembly line. The state of S = R = 1 is therefore "illegal" and should never be entered.
When the device is powered up, a similar condition occurs, because both outputs, Q and Q, are low. Again, the device will quickly exit the metastable state due to differences between the two gates, but it's impossible to predict which of Q and Q will end up high. To avoid spurious actions, you should always set SR flip-flops to a known initial state before using them – you must not assume that they will initialise to a low state.
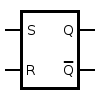
In general, RS Flip Flop has a symbol and a truth table as shown
S R Q Q 0 0 Latch 0 1 0 1 1 0 1 0 1 1 Metastable
Gated SR latch
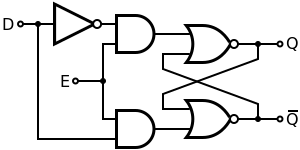
[edit | edit source]In some situations it may be desirable to dictate when the latch can and cannot latch. The gated SR latch is a simple extension of the SR latch which provides an Enable line which must be driven high before data can be latched. Even though a control line is now required, the SR latch is not synchronous, because the inputs can change the output even in the middle of an enable pulse.
When the Enable input is low, then the outputs from the AND gates must also be low, thus the Q and Q outputs remain latched to the previous data. Only when the enable input is high can the state of the latch change, as shown in the truth table. When the enable line is asserted, a gated SR latch is identical in operation to an SR latch.
The Enable line is sometimes a clock signal, but is usually a read or write strobe.
| Enable | S | R | Q | Q | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | Latch | ||
| 0 | 0 | 1 | Latch | ||
| 0 | 1 | 0 | Latch | ||
| 0 | 1 | 1 | Latch | ||
| 1 | 0 | 0 | Latch | ||
| 1 | 0 | 1 | 0 | 1 | |
| 1 | 1 | 0 | 1 | 0 | |
| 1 | 1 | 1 | Metastable | ||
D latch
[edit | edit source]The D latch (D for "data") or transparent latch is a simple extension of the gated SR latch that removes the possibility of invalid input states.
Since the gated SR latch allows us to latch the output without using the S or R inputs, we can remove one of the inputs by driving both the Set and Reset inputs with a complementary driver: we remove one input and automatically make it the inverse of the remaining input.
The D latch outputs the D input whenever the Enable line is high, otherwise the output is whatever the D input was when the Enable input was last high. This is why it is also known as a transparent latch – when Enable is asserted, the latch is said to be "transparent" – it signals propagate directly through it as if it isn't there.
| Enable | D | Q | Q | |
|---|---|---|---|---|
| 0 | 0 | Latch | ||
| 0 | 1 | Latch | ||
| 1 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 0 | |
D latches are often used in I/O ports of integrated circuits and are available as discrete devices, often multiply packaged. An example is the 74HC75, part of the 7400 series of ICs, containing four separate D latches.
SR Flip Flops
[edit | edit source]The fundamental latch is the simple SR flip-flop , where S and R stand for set and reset respectively. It can be constructed from a pair of cross-coupled NOR logic gates. The stored bit is present on the output marked Q.
Normally, in storage mode, the S and R inputs are both low, and feedback maintains the Q and Q outputs in a constant state, with Q the complement of Q. If S (Set) is pulsed high while R is held low, then the Q output is forced high, and stays high even after S returns low; similarly, if R (Reset) is pulsed high while S is held low, then the Q output is forced low, and stays low even after R returns low.
| SR Flip-Flop operation [1] | |||||||
|---|---|---|---|---|---|---|---|
| State transition table | Excitation table | ||||||
| S | R | Action | Q(t) | Q(t+1) | S | R | Action |
| 0 | 0 | Keep state | 0 | 0 | 0 | X | No change |
| 0 | 1 | Q = 0 | 0 | 1 | 1 | 0 | Set |
| 1 | 0 | Q = 1 | 1 | 0 | 0 | 1 | Reset |
| 1 | 1 | Unstable combination, see race condition |
1 | 1 | X | 0 | No change |
('X' denotes a Don't care condition; meaning the signal is irrelevant)
D Flip Flops
[edit | edit source]The Q output always takes on the state of the D input at the moment of a rising clock edge. (or falling edge if the clock input is active low)[2] It is called the D flip-flop for this reason, since the output takes the value of the D input or Data input, and Delays it by one clock count. The D flip-flop can be interpreted as a primitive memory cell, zero-order hold, or delay line.
Truth table:
Clock D Q Qprev Rising edge 0 0 X Rising edge 1 1 X Non-Rising X Qprev
('X' denotes a Don't care condition, meaning the signal is irrelevant)
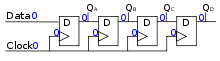
These flip flops are very useful, as they form the basis for shift registers, which are an essential part of many electronic devices. The advantage of the D flip-flop over the D-type latch is that it "captures" the signal at the moment the clock goes high, and subsequent changes of the data line do not influence Q until the next rising clock edge. An exception is that some flip-flops have a 'reset' signal input, which will reset Q (to zero), and may be either asynchronous or synchronous with the clock.
The above circuit shifts the contents of the register to the right, one bit position on each active transition of the clock. The input X is shifted into the leftmost bit position.
Toggle Flip Flops
[edit | edit source]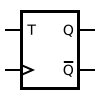 If the T input is high, the T flip-flop changes state ("toggles") whenever the clock input is strobed. If the T input is low, the flip-flop holds the previous value. This behavior is described by the characteristic equation:
If the T input is high, the T flip-flop changes state ("toggles") whenever the clock input is strobed. If the T input is low, the flip-flop holds the previous value. This behavior is described by the characteristic equation:
- (or, without benefit of the XOR operator, the equivalent: )
and can be described in a truth table:
| T Flip-Flop operation [1] | ||||||||
|---|---|---|---|---|---|---|---|---|
| Characteristic table | Excitation table | |||||||
| Comment | Comment | |||||||
| 0 | 0 | 0 | hold state(no clk) | 0 | 0 | 0 | No change | |
| 0 | 1 | 1 | hold state(no clk) | 1 | 1 | 0 | No change | |
| 1 | 0 | 1 | toggle | 0 | 1 | 1 | Complement | |
| 1 | 1 | 0 | toggle | 1 | 0 | 1 | Complement | |
When T is held high, the toggle flip-flop divides the clock frequency by two; that is, if clock frequency is 4 MHz, the output frequency obtained from the flip-flop will be 2 MHz. This 'divide by' feature has application in various types of digital counters. A T flip-flop can also be built using a JK flip-flop (J & K pins are connected together and act as T) or D flip-flop (T input and Qprevious is connected to the D input through an XOR gate).
JK Flip Flops
[edit | edit source]The JK flip-flop augments the behavior of the SR flip-flop (J=Set, K=Reset) by interpreting the S = R = 1 condition as a "flip" or toggle command. Specifically, the combination J = 1, K = 0 is a command to set the flip-flop; the combination J = 0, K = 1 is a command to reset the flip-flop; and the combination J = K = 1 is a command to toggle the flip-flop, i.e., change its output to the logical complement of its current value. Setting J = K = 0 does NOT result in a D flip-flop, but rather, will hold the current state. To synthesize a D flip-flop, simply set K equal to the complement of J. The JK flip-flop is therefore a universal flip-flop, because it can be configured to work as an SR flip-flop, a D flip-flop, or a T flip-flop. NOTE: The flip flop is positive edge triggered (Clock Pulse) as seen in the timing diagram.
The characteristic equation of the JK flip-flop is:
and the corresponding truth table is:
| JK Flip Flop operation [1] | ||||||||
|---|---|---|---|---|---|---|---|---|
| Characteristic table | Excitation table | |||||||
| J | K | Qnext | Comment | Q | Qnext | J | K | Comment |
| 0 | 0 | hold state | 0 | 0 | 0 | X | No change | |
| 0 | 1 | reset | 0 | 1 | 1 | X | Set | |
| 1 | 0 | set | 1 | 0 | X | 1 | Reset | |
| 1 | 1 | toggle | 1 | 1 | X | 0 | No change | |
References
[edit | edit source]- ↑ a b c Mano, M. Morris (2004). Logic and Computer Design Fundamentals, 3rd Edition. Upper Saddle River, NJ, USA: Pearson Education International. pp. pg283. ISBN 0-13-191165-1.
{{cite book}}:|pages=has extra text (help); Unknown parameter|coauthors=ignored (|author=suggested) (help) - ↑ The D Flip-Flop