Transportation Geography and Network Science/Public transit networks
Background[edit | edit source]
The Wikipedia page on public transit provides a brief overview on what transit is and how it works.
Capacity[edit | edit source]
Public transit increases the theoretical passenger capacity of roads by consolidating passengers into fewer vehicles. The graphs to the right depict the vehicle and passenger capacity for a road capable of accommodating 1,800 cars or car equivalents per hour. In this hypothetical example, a car carries 1.8 passengers and a bus carries 47 passengers while occupying the space of two cars. This results in a road capacity of 3,240 passengers if all travel by cars or 42,300 if all travel by bus.[1]
Gordon Newell's notes on public transportation calculate the necessity for Bay Area Rapid Transit (BART) to serve workers in San Francisco's financial district.[2] Newell estimates that the financial district attracts 200,000 in-bound trips to a 1 square mile area. Given the typical number of roads serving one square mile (10 city blocks), Newell calculates the theoretical maximum number of vehicles that could enter the area (parking considerations aside) to be 40,000 cars per hour.[2] Transit is an essential component of central business district (CBD) configurations with very high job densities such as the SF financial district.
Modes[edit | edit source]
Numerous types of transit modes exist, serving a range of needs, capacities, and scales. Fixed route service is provided by buses, streetcars, or rail. They can operate in mixed traffic, special lanes, or exclusive right-of-ways. Demand responsive transport, e.g., Paratransit, uses the same roadways as private autos.
Comparison of modes by passenger capacity and average speed[3][edit | edit source]
| Mode | Peak Capacity (passengers/hour) | Average Speed (miles/hour) |
|---|---|---|
| Bus in mixed traffic | 500-1,500 | 3-6 |
| CBD bus lane | 2,000-9,000 | 4-8 |
| LRT on street | 1,800-28,000 | 8-16 |
| People mover | 1,500-6,000 | 8-22 |
| Commuter Rail | 2,000-20,000 | 20-50 |
| LRT exclusive right of way | 8,000-25,000 | 25-35 |
| Busway | 2,000-10,000 | 35-45 |
| Bus on HOV lane | 4,000-8,000 | 35-55 |
| Heavy Rail | 13,000-49,000 | 35-55 |
Public transit as a network[edit | edit source]
Derrible and Kennedy (2010)[4] document how transit networks can be represented as graphs which reveal ways they differ from other transportation networks. Their work focuses on passenger rail metro systems for simplicity, but these concepts can also be applied to bus networks and other forms of fixed-route public transit. Transit networks consist of lines that connect multiple edges. Some lines can overlap which presents challenges in graphing and analyzing.
Graphing transit networks[edit | edit source]
Vertices[edit | edit source]
Vertices can represent either all nodes (stations) or only nodes that are transfer points and termini. The former allows for analyzing average stop spacing and the regional or local focus of the network. Derrible and Kennedy focus on the latter definition because it more accurately represents the network design.[4] Vertices are subdivided into end-vertices () and transfer-vertices () such that .
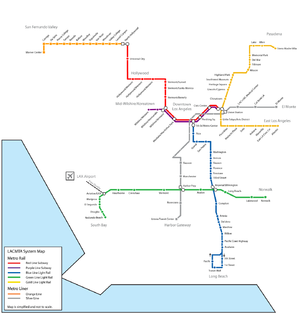
In the example graph of the LA Metro network[note 1], there are 6 lines with a total of 83 nodes. 7 are terminal points () and 5 are transfer points between 1 or more lines (), totaling 12 vertices ().
Edges[edit | edit source]
Since transit lines can overlap, edges are classified as either "single" () or "multiple" () to isolate redundancies [4]. The LA Metro example contains 11 single edges and 2 multiple edges (, , ).
Measuring public transit networks[edit | edit source]
Maximum number of transfers[edit | edit source]
Network diameter is usually a measure of the shortest path between the two most distant vertices in the network. In transit networks, however, the number of transfers is a more meaningful indicator of travel friction. Thus Derrible and Kennedy use the maximum number of transfers required to complete the longest journey in a transit network as their measure of network diameter. [4]
In the Los Angeles Metro map pictured, the maximum number of transfers is 3. Trips that start along the green line and end in the Valley, Pasadena, or East LA (or the reverse journey) require three different transfers. All other OD pairs require two or fewer transfers.
State of development[edit | edit source]
Derrible and Kennedy use the Beta Index to measure the developmental stage of the transit network. [4] The beta index is simply a ratio of links to nodes in the network. Trees and simple networks have values smaller than one, and more complex networks have values higher than one. This developmental measure assumes that transit networks start with radial edges and add cross-town links as they develop and demand increases.
In the Los Angeles metro network pictured, the beta index value is about 0.92, which is consistent with the aforementioned interpretation of beta index values below 1. When double edges are treated as a single edge, the network is a perfect tree.
Network Orientation[edit | edit source]
Average stop spacing and average line length can be used to gauge the focus of a transit network. Longer lines and more distant stops suggest that the network is serving longer distance commuters, while smaller values of each indicate a local network, such as a streetcar system.[4]
Public transit network attributes[edit | edit source]
Scale-free[edit | edit source]
Derrible and Kennedy tested the networks of 19 urban rail transit networks to look for scale-free network features.[5] Of these, 14 systems followed a power law distribution for the number of lines hosted by each station.
Small world[edit | edit source]
Derrible and Kennedy also tested urban rail transit networks to see if they were small-world networks: networks with a high degree of clustering and a small average shortest-path length.[5] Since urban rail networks are planar and typically small graphs, Derrible and Kennedy use the number of transfers rather than the absolute distance for the "shortest path length". They find that the urban rail networks in their study are in fact small-world networks, and become increasingly more connected as they grow in size.[5]
Public transit versus other transportation networks[edit | edit source]
Public transit networks differ from other types of transportation networks in some key respects. Most notably, since public transit services are typically provided on fixed schedules and fixed routes in urban settings, they lack the temporal and spatial ubiquity of road networks. For instance, if I want to make a trip by car in an urban area, all I need is a vehicle and a valid driver's license. I can access the network virtually anywhere and travel to most destinations within the area in a reasonable amount of time. By contrast, if I wish to make a trip between two points in an urban area by public transit, I have to go to a place that is served by the network at the times that service is available.
The supply of public transit services, and hence the extent of the network, varies both by time of day (rush hour versus non-rush hour) and by day of the week (weekdays versus Saturday/Sunday), and is roughly in proportion to demand. Since much of the demand for public transit is concentrated during conventional peak travel periods on weekdays, there are often major differences in service levels between peak and off-peak (midday, evening, and late night) periods. For example, in 2009 Metro Transit (the largest transit provider in the Minneapolis-St. Paul region) operated a fleet of 735 buses during the PM peak period, the period of greatest demand. During the midday period it had on average only 292 buses in service. The corresponding figures for Saturday and Sunday, which do not tend to exhibit the same sharp peaks in demand during the day, are 235 and 166 buses, respectively.
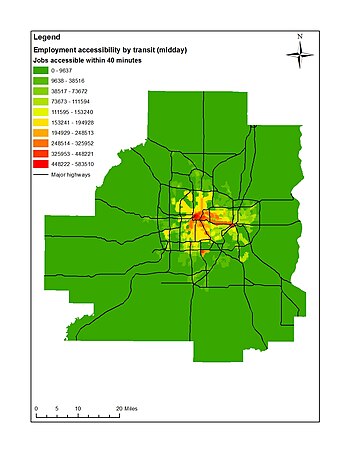
Another way to illustrate the temporal variations in the level of service provided by the public transit network is to look at the level of accessibility it provides at different times. The figures at right shows the level of accessibility to jobs provided by the public transit network in 2005 in the Minneapolis-St. Paul, MN (Twin Cities) region during the midday and PM peak periods. The locations denoted by the "hotter" colors (red/orange/yellow) have higher levels of accessibility, while the "cooler" colors (shades of green) represent locations with lower accessibility. The biggest differences between peak and off-peak accessibility appear to be in suburban areas, where some locations only receive service during peak periods (e.g. commuter buses) and others receive significantly more frequent service.
Travel along public transit networks tends to disaggregate the typical trip into several segments. Whereas I might be able to simply walk out of my house to access my car, I will need to walk to the nearest bus stop or train station if I wish to use public transit. If there isn't a stop within walking distance of my house I might need to bike, get a ride, or drive to a nearby park-and-ride facility in order to access the transit network. In some cases this may represent a significant component of overall travel time. Apart from access time, transit trips also require waiting time. Passengers often wish to arrive at a bus stop a few minutes prior to the scheduled departure time as a response to travel time uncertainty. The penalty for missing a particular trip will likely be greater on routes with less frequent service. It is commonly observed in practice that wait times at stops are systematically related to the frequency of service. Longer or multi-directional trips by public transit often require transfers which in most cases results in additional waiting and in-vehicle time (though in certain cases timed transfers can be arranged at transfer points to minimize the inconvenience. Finally, a passenger's destination may or may not be next to a transit stop, and so some time may be spent in egress once they have alighted from the bus or train.

A key feature of the design of transportation networks is the ability to exploit scale economies. Scale economies exist where the marginal cost of producing another unit of output falls below the average cost over some range of output. For most types of transportation networks, scale economies arise from the ability to spread some fixed cost of the network out across a large number of users. The basic example is road networks, where much of the cost of providing a road is fixed (at least in the short term). Thus, for greater numbers of users, the average cost per user will fall and marginal costs become very low, up to the point where congestion sets in. Likewise, airlines may derive scale economies from more intensive use of its fixed infrastructure, e.g., airports runways and terminals.
Sources of Scale Economies in Public Transit Networks[edit | edit source]
A traditional argument for the public provision of transit services has held that production of services is subject to strong economies of scale, and hence may have some characteristics of a natural monopoly. The measurement of scale economies, which typically involves analyzing the behavior of the cost function with respect to some measure of output, is complicated in the case of public transit networks. This is due to the fact that 1) there are multiple types of outputs and 2) outputs are produced on a network, implying that there are different ways in which output levels can change.
The former argument, that there are multiple types of output, is an important one. Analysts often distinguish between produced outputs, such as vehicle-miles, and consumed outputs, such as passenger boardings or passenger-miles of travel. This distinction matters since produced outputs tend to relate to service levels, while consumed outputs are more closely related to service utilization, and hence are more commonly found to be a source of scale economies.
The latter argument, that transit services are produced on networks, gives rise to another distinction in the measurement of scale economies. In principle, it is possible to expand the (produced) output of public transit networks in two different ways. The first is to expand the size of the network, say by adding a new link while holding the flows on the rest of the links constant. The second is to increase the flows on the existing links of a network while holding the size of the network constant. If average costs are declining in the long run, we would say the first case is an example of economies of size, while the second case is an example of economies of traffic density.
Most of the evidence that has been collected on bus systems suggests that returns to scale are approximately constant, though there is some evidence of increasing returns with respect to passenger flows and capacity utilization[6][7]. This makes sense, since most buses can handle additional passengers at little additional cost up to the point that a unit of capacity (bus) is used up. Rail systems are typically assumed to exhibit greater economies of scale due to their larger fixed costs and higher capacities. A study by Savage[8] examined a sample of US heavy and light rail systems and found evidence of fairly large economies of traffic density when looking at variable costs, but found only constant returns with respect to system size.
The "Mohring Effect"[edit | edit source]
Up to this point, we have only been considering the costs that are faced by the providers of public transit services. However, it turns out that one of the most critical components of cost when analyzing public transit networks is the time cost that users of the system face. A seminal paper by Mohring[9] demonstrated that public transit networks may be subject to scale economies if the definition of cost is expanded to include user time costs. Mohring showed that if transit operators respond to an increase in demand by increasing service levels (i.e. by reducing the headway between buses) or by increasing the density of coverage of the network, that total costs could fall via reductions in the access and waiting times users face. This phenomenon has come to be known as the Mohring effect. To the extent that the savings in user cost translate into increased ridership, the Mohring effect can be seen as an example of a positive feedback system. This source of increasing returns has been seldom exploited in practice however, at least in many US cities, due to lower average population densities and hence fewer suitable corridors for operation[10].
Optimal Transit Networks[edit | edit source]
The existence of scale economies with respect to user costs has implications for the design of optimal transit networks. In particular, it suggests that networks ought to be designed to be more convenient for users, with routes and stops being sited to reduce access and waiting times, which empirical research has shown to be valued more highly (i.e. have greater disutility) than in-vehicle time[11]. Designs which reduce costs to users tend to involve tradeoffs in the form of higher agency or provider costs, as more vehicles must be deployed and/or capital investment sunk into the network.
The Transit Network Design Problem[edit | edit source]
The evaluation of these design considerations can be formulated mathematically and solved as an optimization problem in order to determine the parameters of transit networks that are in some sense "optimal". This type of problem is commonly known as a network design problem, or NDP. The public transit version of the NDP is complicated by the intermittent nature of transit services, that is, the fact that fixed-route transit tends to rely on pulse scheduling. Thus, the design problem often involves several decision variables, such as route and stop spacing, frequency of service (headway) and in certain cases, fare levels. Numerous different variants of the transit NDP have appeared in the published literature on engineering, transportation, and operations research. A recent review of this literature[12] has suggested that the many studies can be synthesized and categorized according to three main criteria:
- Objectives, which denote the element of the system to be optimized, e.g., social cost, total welfare, transit use.
- Parameters, the attributes which characterize a public transit network. These can be further classified according to decision variables (route or stop spacing, service frequency, number and/or size of vehicles), network structure (rectangular grid, irregular grid, radial), demand patterns (many-to-one, many-to-many), and demand characteristics (fixed, elastic, time/space/service dependent).
- Solution method, which describes the method used to solve the mathematical problem that characterizes the design of the network. Some problems are simple enough to be solved analytically, others require heuristics or more elaborate numerical methods, such as linear or nonlinear programming and various solution algorithms.
Competitive Transit Networks[edit | edit source]
Most of the papers that analyze the transit NDP do not consider transit mode as a design parameter of the network. One recent study by Daganzo[13] sought to compare modes within the general framework of the transit NDP. The study was described as an effort to identify the characteristics of "competitive" transit networks, with competitiveness referring to the ability of the network to provide a level of service comparable to that of the private auto, and was conducted with an emphasis toward applying the findings to real-world settings.
The study focused on an idealized service area with a perfectly square shape and uniform patterns of demand. Three modes were considered: regular bus, bus rapid transit and metro/heavy rail, each with certain infrastructure and access cost characteristics. The objective function, which was to be minimized, was expressed in terms of total costs, defined as the sum of agency costs (infrastructure, vehicle fleet, and mileage-related costs) and user costs (walking access, waiting, transfer, and in-vehicle time costs, plus mileage-related costs). For each mode, the model was solved for three time-independent decision variables: stop spacing, service frequency (headway) and the structure of the network, which was characterized by a parameter indicating the degree to which the network resembled a grid versus a hub-and-spoke network. In each case, total costs were converted into units of user time to permit comparisons across transit modes as well as comparisons with an auto-based alternative. The square service area was characterized by parameters describing its dimension (size) and its level of demand intensity. Both of these parameters were allowed to vary in order to test scenarios which represented different combinations of city size and demand intensity.
The results indicated that in every scenario user cost represented a large share of total costs, confirming the findings of Mohring and other analysts who have stressed the importance of user costs in optimal transit design. Among the modes, the bus rapid transit option was found to be competitive under a variety of different circumstances (excluding big cities with low demand intensity) and tended toward a more grid-like network structure. Systems with more expensive infrastructure, especially the metro mode, tended to favor network structures closer to the hub-and-spoke concept. The study also observed a critical level of stop spacing, beyond which both user and agency costs would increase. Commenting on the results of the study, which indicated the superiority of BRT under a range of scenarios, Daganzo suggested that the proliferation of metro systems, especially in European cities, reflects the lack of suitable streets (and public support) for running a BRT network with the coverage and frequency characteristics that described the optimal solutions in each scenario.
Notes[edit | edit source]
- ↑ Example models only the 6 lines with exclusive right-of-ways: 2 subway lines (red and purple), 3 LRT lines (gold, green, blue), and 1 BRT line (orange)
References[edit | edit source]
- ↑ Example scenario used as an assignment in PA 5231, Fall 2010, with Professor Jason Cao. Charts made by Jessica Schoner and submitted in a group paper with Laura Eash and Eric Gunderson.
- ↑ a b Newell, Gordon F. 1994. Lecture Notes on Public Transportation.
- ↑ Transit Capacity and Quality of Service Manual, 2nd Edition
- ↑ a b c d e f Derrible, S. & Kennedy, C. 2010. Characterizing metro networks: state, form, and structure. Transportation 37:275-297.
- ↑ a b c Derrible, S. & Kennedy, C. 2010. The complexity and robustness of metro networks. Physica A 389: 3678-3691.
- ↑ Karlaftis, Matthew G.; McCarthy, Patrick (2002). "Cost structures of public transit systems: a panel data analysis". Transportation Research, Part E: Logistics and Transportation Review. 38 (1): 1–18. doi:10.1016/S1366-5545(01)00006-0.
{{cite journal}}: Unknown parameter|month=ignored (help) - ↑ Harmatuck, Donald J. (2005). "Cost functions and efficiency estimates of Midwest bus transit systems". Transportation Research Record. 1932: 43–53. doi:10.3141/1932-06.
- ↑ Savage, Ian (1997). "Scale economies in United States rail transit systems". Transportation Research, Part A: Policy and Practice. 31 (6): 459–473. doi:10.1016/S0965-8564(97)00003-7.
{{cite journal}}: Unknown parameter|month=ignored (help) - ↑ Mohring, Herbert (1972). "Optimization and scale economies in urban bus transportation". American Economic Review. 62 (4): 591–604.
{{cite journal}}: Unknown parameter|month=ignored (help) - ↑ Small, Kenneth A. (1997). "Economics and urban transportation policy in the United States". Regional Science and Urban Economics. 27 (6): 671–691. doi:10.1016/S0166-0462(96)02166-7.
{{cite journal}}: Unknown parameter|month=ignored (help) - ↑ Wardman, Mark (2004). "Public transport values of time". Transport Policy. 11 (4): 363–377. doi:10.1016/j.tranpol.2004.05.001.
{{cite journal}}: Unknown parameter|month=ignored (help) - ↑ Kepaptsoglou, Konstantinos; Karlaftis, Matthew (2009). "Transit route network design problem: review". ASCE Journal of Transportation Engineering. 135 (8): 491-505. doi:10.1061/(ASCE)0733-947X(2009)135:8(491).
{{cite journal}}: Unknown parameter|month=ignored (help) - ↑ Daganzo, Carlos F. (2010). "Structure of competitive transit networks". Transportation Research, Part B: Methodological. 44 (4): 434–446. doi:10.1016/j.trb.2009.11.001.
{{cite journal}}: Unknown parameter|month=ignored (help)