Structural Biochemistry/Proteins/NMR Spectroscopy
NMM spectroscopy is unique in being able to reveal the atomic structure of macromolecules in solution, provided that highly concentrated solution can be obtained. This technique depends on the fact that certain atomic nuclei are intrinsically magnetic. The chemical shift of nuclei depends on their local environment. Furthermore, the spins of neighboring nuclei interact with each other in ways that provide definitive structural information. This information can be used to determine complete three-dimensional structures of proteins.
General Information[edit | edit source]
Nuclear Magnetic Resonance Spectroscopy (NMR) is an analytical technique which exploits the fact that certain nuclei possess a property called spin (I). NMR spectroscopy is possible due to the Zeeman Effect discovered first in the 1890s. The structures of proteins can be determined by NMR by first preparing the isotopically labeled samples. In the magnet, the "natural magnets" in the atoms of the sample line up with the magnetic field of the NMR magnet. Then, the sample is exposed to a series of radio wave pulses to disrupt the magnetic equilibrium of the atoms. The reaction of these nuclei can be observed to assess their chemical nature specifically, their chemical shift properties. Sets of experiments can be conducted to refine possible structures and present the average of the experiments as the final structure. It can have advantages over X-ray crystallography because the samples of proteins can be in solution rather than crystallized form and other properties of the sample protein, such as flexibility and interactions, can be determined while X-ray crystallography only reveals the structure of the protein.
It is the splitting of atomic energy levels when the atoms are placed in a magnetic field. This effect was later found to occur as a result of nuclear spin. In 1924, Wolfgang Pauli first suggested the theoretical basis of NMR when he concluded that some atomic nuclei should possess nuclear spin and these nuclei would split into degenerate energy levels when placed in a magnetic field. These nuclei have a magnetic moment, in and of themselves, which is called spin. Nuclei that possess spin are said to be NMR active. Some NMR active nuclei can be seen in Table 1, with italicized nuclei being those commonly studied in biological molecules.

Separately, Bolch at Stanford and Purcell at Harvard in 1946 each translated the Zeeman effect into the first NMR spectrum. In 1949, Proctor and Yu at Stanford measured the first chemical shift and spin couplings. Initially, commercial NMR spectrometers were continuous wave type and were only able to detect the most sensitive nuclei, 1H & 19F. NMR ‘active’ nuclei are active if the nuclear spin, I, is non zero.
To determine spin of nuclei:
Mass # is even and # neutrons is even, I=0, therefore no spin
Mass # is even and # neutrons is odd, I= integer, therefore spin
Mass # is odd and # neutrons is even or odd, I=half integer, therefore spin
The cause of spin can be visualized with the following analogy. A rotating charged particle (e.g. hydrogen nucleus aka proton) will produce a magnetic field perpendicular to the direction of rotation which is analogous to the magnetic field of a bar magnet, as seen in Figure 1.

Absent an external magnetic field (B¬0) these active nuclei are oriented in random directions, but in the presence of an external magnetic field (B¬0) these nuclei orient themselves either with or against the field, as seen in Figure 2.

Nuclei are dispersed between states of different energies. The different energy levels are induced by the presence of the external magnetic field (B¬0). (For spin ½ nuclei two orientations are possible, with the higher energy orientation being ‘β spin state’ and the lower energy orientation being ‘α spin state’.) This is evident in the following equation where E=energy, h=Planck’s constant, ν=frequency, γ=gyromagnetic ratio (nucleus dependent), B0= external magnetic field:
ΔE= h ν = γ B0
To see this graphically see Figure 3.

These induced energy level differences are what allow the use of NMR. At equilibrium, nuclei will occupy both levels of energy, low and high. However, according to the Maxwell-Boltzmann Distribution, the lower energy level will be occupied by a greater number of nuclei. This difference in the number of nuclei, between low and high energy levels, is what NMR exploits. The energy required to cause a spin flip, transition from low to high energy state, corresponds to the radio frequency range of the electromagnetic spectrum. ΔE= h ν A nucleus will only flip spins, absorb energy, when the frequency of electromagnetic radiation just matches the change in energy, ΔE. This is called the point of resonance. Nuclei will have differing resonant frequencies based on their local electronic environment. This can be seen in “A handmade example of a proton (1H) NMR spectrum.” All nuclei under observation are irradiated with radio waves to the higher energy state and are then allowed to decay back to the lower energy state. This decay is what is observed. A free induction decay signal is collected as the nuclei fall back to the lower energy state, Figure 4 depicts a generic FID.

This FID is then subjected to a Fourier transform to convert from the time domain to the frequency domain, seen in Figure 5.

A change in the magnitude of the magnetic field will change the resonant frequency of the nucleus. Therefore, in order to compare spectra between instruments with varying size magnetic strength it is necessary to convert from frequency to parts per million, ppm. This can be done with the equation seen in Figure 6.

With the arrival of Fourier Transform instruments in the 1970s it became possible to acquire spectra of nuclei that are not naturally abundant, such as 13C which is only 1.1% naturally occurring. This requires the acquisition of multiple spectra and adding them together to get a greater sensitivity. The signal to noise ratio (S/N) will increase as acquisitions increase, because the signal magnitude increases linearly with acquisition number while the noise magnitude increases as the square of the number acquisitions. So, the S/N will increase as the square of the number of acquisitions as seen in Figure 7.

The Nobel Prize in Chemistry 2002 went partly to Kurt Wuthrich for “NMR Studies of Structure and Function of Biological Macromolecules,”[1] so NMR is important to structural biochemistry. Table 2 lists Nobel prizes awarded for discoveries related to NMR spectroscopy.


NMR is a powerful technique that can be used to determine the structure of proteins in highly concentrated solution, by analyzing the relative positions of certain atoms (Shriner 136). Protein NMR exploits the absence of zero net nuclear spin of the most abundant isotopes of carbon and oxygen (12 and 16) as well as the abundant isotope of Nitrogen (14) with a net nuclear spin of 1. NMR cannot be performed on an atom with zero net nuclear spin. Since there are many distinct nuclei present in a single protein much overlap is expected in the chemical shifts produced through the NMR analysis therefore a multidimensional approach is applied. Magnetization is applied to the protein and nuclei through electromagnetic pulses that can magnetize nuclei in two ways. The first involving magnetization through nuclei bonding and the second through open space. Each approach offers a different way to analyze the protein such as the first approach allowing for distinct nuclei to be targeted whereas the second approach allowing for structure calculation distance restraints and targeting an unlabeled protein.
Intrinsically magnetic nuclei display spinning properties that produce a magnetic moment. When an external magnetic field is applied to the system the magnetic moment can adopt either an alpha or beta state. The strength of the magnetic field determines the proportionality of alpha to beta with a tendency to favor alpha as it is aligned with the field and has a lower energy. By supplying an electromagnetic pulse alpha spin nuclei will change to beta and produce resonance. By keeping a constant magnetic field on the system and adjusting the frequency of the electromagnetic pulses a spectrum of resonance can be obtained.
Currently, NMR spectrometers use the Fourier transform method of pulse radiation. To change the nuclei in alpha state to beta, a strong pulse of radiation is used. Then the pulse of radiation is removed and the nuclei go back to their original alpha state, giving a decay signal. This signal is converted by the computer to a frequency domain spectrum in a very fast way. By storing many signals a more intense spectrum is produced. (Shriner 136)
Electrons around a magnetic nucleus produces a local magnetic field opposite to the applied magnetic field. Magnetic nuclei can absorb the electromagnetic pulses at specific frequencies coined "chemical shifts" (signal positions) expressed in parts per million (ppm). These chemical shifts are designated relative to a standard compound such as a derivative of tetramethylsilane (TMS) (CH3)4Si (which has a chemical shift of 0.0) that is soluble in water. NMR spectra that are produced through this assay can be analyzed, and with the combination of a multidimensional analysis the structure of the protein can be determined.
When an atomic nuclei is influenced by a magnetic field, it creates a magnetic moment which will give an orientation of spinning to itself. Different orientation of spinning, spin states, exist in different states of energy - alpha-state and beta-state - where alpha-state is found to be more stable with a lower energy through experiments as it has the same direction with the magnetic field. In order to transits alpha-state to beta-state (excited state), pulse of electromagnetic radiation is needed to increase the frequency of the electromagnetic radiation (through irradiation) to have the spinning nucleus to overcome the energy barrier and change its orientation. (See Bohr Model for more information) Thus, resonance will be obtained. It was discovered by American physicist Edward Mills Purcell and physicist Felix Bloch from Switzerland in 1946.
The difference between energy levels split by a magnetic field corresponds to the energy of radio waves. So, the electronics required for the NMR spectrometer weren’t developed until WWII when the government invested heavily into radar technology. Radar is simply the use of radio waves to detect location and direction of moving objects. Better frequency synthesizers, amplifiers, receivers and signal processors all contributed to advancements in the field of NMR spectroscopy. The components of a NMR Spectrometer can be seen in Figure 8.

Some common 2D experiments can be seen in Table 3:
| Common 20 experiments (Table 3) | |
|---|---|
| COSY | Correlated Spectroscopy Through bond H-H correlation |
| TOCSY | Total Correlation Spectroscopy Extended through bond H-H correlation |
| 1D NOE | Nuclear Overhauser Effect Spectroscopy H-H through space correlation |
| NOESY | Nuclear Overhauser Effect Spectroscopy H-H through space correlation |
| ROESY | Rotating Frame Overhauser Effect Spectroscopy Similar to NOESY |
Magnets used for NMR[edit | edit source]
The magnets used for NMR are very strong. Those used for high resolution protein structure determination range from 500 megahertz to 900 megahertz and generate magnetic fields thousands of times stronger than the Earth’s. Although the sample is exposed to a strong magnetic field, very little magnetic force gets out of the machine. NMR magnets are superconductors, so they must be cooled with liquid helium, which is kept at 4 Kelvin. Liquid nitrogen, which is kept at 77 Kelvin, helps keep the liquid helium cold.
Appropriate Isotopes[edit | edit source]
Only certain isotopes are capable for use in NMR. The most common isotope that is used in NMR is Hydrogen-1 (Proton NMR). Other commonly used isotopes are Carbon-13 and Nitrogen-15.
Vector Model[edit | edit source]
The Vector Model only holds for uncoupled spins. Nuclei that are active under NMR spectroscopy have associated with them a nuclear spin magnetic moment, which means that these nuclei produce a small magnetic field. When these nuclei are placed in a magnetic field the energy of the interaction depends on the angle between the field and the magnetic moment. The highest energy interaction is when the magnetic field and the magnetic moment point in opposite directions, and the lowest energy interaction is when the magnetic field and magnetic moment point in the same direction. Before a magnetic field is applied to a population of nuclei the magnetic moments of these nuclei are oriented randomly due to random thermal motion. After a magnetic field is applied one has to wait for the spins to come to equilibrium, a process known as relaxation. Pointing in the direction of the magnetic field is slightly energetically favored, and hence only a very small number of spins will do so, forming the bulk magnetization vector. The sample is hence magnetized. At equilibrium the bulk magnetization vector will point in the direction of the magnetic field (we will assume this is the z direction) and will be stationery. If the magnetization vector was tilted away from the axis it would precess at the Larmor frequency (-gyromagnetic ratio * magnetic field). The purpose of a pulse is to quickly change the direction of the magnetization vector. This can be done by creating a much weaker magnetic field in the direction one desires, but allowing it to oscillate at the aforementioned Larmor frequency. This will result in the magnetization vector pointing in the direction one desires. This occurs because when the B1 field (the weaker field) oscillates near the Larmor Frequency, the result is that the strength of the B0 field (the stronger field in the z direction) appears to be reduced. Hence the resulting magnetic field (the effective field) can point very close to the direction of the B1 field if the B1 field is much larger than the reduced field. An on resonance pulse involves changing the direction of the magnetization vector by applying the B1 field in a certain direction for a specific time. The angle through which the magnetization vector is rotated is given as the product of the frequency of the effective field and the time the pulse is applied. By applying different times one can rotate the magnetization vector to different angles. For a real NMR experiment there are going to be more than one resonance frequencies in the sample. If one makes the B1 field strong enough it is possible to bring the magnetization vector very close to the desired orientation, which means we can bring it close to the ideal case of an on resonance pulse. The vector model can be used to understand simple NMR experiments.
Chemical shifts[edit | edit source]
Chemical shifts are the units used in Protein NMR analysis graphs. Chemical shift correlates to the different radiofrequency electromagnetic pulses sent through the protein sample. Each molecule that exhibits spin properties show different distinct chemical shifts. Chemical shifts can be observed by sending nuclear magnetic energy onto the protein sample. The electron clouds that surround each spin nuclei create a local magnetic field that opposes the applied magnetic field. When the electromagnetic pulse runs through the sample alpha spin nuclei that are hit with the correct amount of energy to switch to beta spin do so and subsequently cause resonance. This resonance can then be recorded and is reported for the different frequencies applied to sample as parts per million (ppm chemical shifts). For example, when the nuclear magnetic field strength sends out a frequency of 1 ppm (parts per million), CH3 reacts to it and exhibits beta spin behavior from which the spectroscopy catches this signal and records it.
Most hydrogen absorptions in 300-MHz 1H NMR fall within a range of 3000 Hz. Rather than record the exact frequency of each resonance, we measure it relative to an internal standard, the compound tetramethylsilane, (CH3)4Si. Its 12 equivalent hydrogens are shielded relative to those in most organic molecules, resulting in a resonance line conveniently removed from the usual spectral range. A problem with these numbers, however, is that they vary with the strength of the applied magnetic field. Because field strength and resonance frequency are directly proportional, doubling or tripling the field strength will double or triple the distance (in hertz) of the observed peaks relative to (CH3)4Si. To make it easier to compare reported literature spectra, we standardize the measured frequency by dividing the distance to (CH3)4Si (in hertz) by the frequency of the spectrometer. This procedure yields a field-independent number, the chemical shift δ.
NMR in Characterizing Organometallics[edit | edit source]
NMR spectra uses superconducting magnets to many metal nuclei. Carbon 13 NMR has become increasingly useful in facilitating due to its low natural abundance and low sensitivity for NMR experiment. The integration of NMR peaks of organometallic complexes can provide the ratio of atoms in different environments. Since the relaxation times of the carbon atoms vary in organometallics, a great deal of inaccuracy result from this. However it does have its advantages as well. For example, terminal carbonyl peaks are frequently in the range of 195 to 225ppm, which allows it to be easily distinguished from other ligands. The 13C chemical shift correspond with the strength of the CO bond. The stronger the bond, the smaller the chemical shift. 13C in cyclopentadienyl ligands have a wide range of chemical shifts in paramagnetic compounds whereas it's narrower for diamagnetic compounds.
Nuclei Spin States[edit | edit source]
In NMR, certain atomic nuclei must be magnetic by nature in order for this technique to be used. However, only a certain number of isotopes have this magnetic characteristic called spin. An example is hydrogen. When an external magnetic field is applied, hydrogen's spinning proton generates a magnetic moment which can take either the α or β spin state. The energy difference between the two states is directly proportional to the amount of external magnetic field applied. The α state is aligned with the applied field and has lower energy than the β state. When a pulse of electromagnetic radiation is applied to the α state, it can be excited to the β state, thus a resonance will be obtained.
The NMR is only able to detect certain atoms and only certain isotopes. For example, it can detect the Hydrogen molecules with a mass of 1 amu, but not the other isotopes. Most commonly the Hydrogen and Carbon NMR's are used. The information that can be determined by the NMR is immense. In the case of the Hydrogen NMR, one can use a certain amount of knowledge from a table to determine what each peak corresponds to which group within your sample. Interpreting NMR's can also be a little tricky in that one must understand splitting patterns. For example, the carbon atom you may be examining may have only one hydrogen attached, however if attached to a methyl group, it will appear as a quartet.
Shielding and Deshielding[edit | edit source]
Protons in different chemical environments are shielded by different amounts. When a nucleus surrounded by electrons is exposed to a magnetic field of strength H0,these electrons move in such a way as to generate a small local magnetic field, hlocal, opposing H0. As a consequence, the total field strength near the hydrogen nucleus is reduced, and the nucleus is thus said to be shielded from the magnetic field strength by its electron cloud. The degree of shielding depends on the amount of electron density surrounding the nucleus. dding electrons increases shielding; their removal, consequently, would cause deshielding. Also, a proton is deshielded when the induced field reinforces the applied field. For example, the induced field can reinforce the applied field. As a result, these protons are deshielded and their chemical shifts are at a higher value of ppm.
Coupling[edit | edit source]
J-coupling arises from the interaction of different spin states through the chemical bonds of a molecule and results in the splitting of NMR signals. This coupling provides detailed information about the connectivity of atoms and the structure of a molecule. Spin-spin slitting is given by the N+1 Rule: 1) H that is neighbored by one H resonnate as a doublet.2) H that is neighbored by two set of equivalent Hs resonate as trplet. 3) H that is neighbored by three equivalents of hydrogens resonate as a quartet.
A multiplet can be shown when there is a mixture of couple patterns, some of which could be broken down to small parts (i.e. qd- quartet of doublet). But for the most part, if a coupling pattern shows complexity not easily countable by N+1 rule, such pattern is called a multiplet. In addition, functional groups containing alcohol (-OH) such as alcohol, carboxylic acid have a broad band on NMR spectra. This is due to the fact that Hydrogens on alcohol can hydrogenbond easily, thus being able to couple in broad spectra than other H's. Thus just by looking at the type of the spectra (such as multiple peaks or broad peak), one can easily categorize the functional group to which the H is associated with.
The ratio of the splitting peaks is given by a mathematical mnemonic device called Pascal's triangle. Each number in this triangle is the sum of the two numbers closest to it in the line above. It is important to remember that nonequivalent nuclei mutually split one another. In other words, the observation of one split absorption necessitates the presence of another split signal in the spectrum. Moreover, the coupling constants for these pattern must be the same. Double and triple bond characteristic chemical environments show complex splitting peaks. An alkyne for example, can have hydrogen splitting patterns an extra adjacent carbon away. An alkene depending on where the hydrogen is located (cis or trans) to a relative chemical environment, can show a slightly distorted peak.
Integration[edit | edit source]
Integration is very useful in NMR spectrum in determining the structure of a molecule. The relative integrated intensity of a signal is proportional to the relative number of nuclei giving rise to that absorption. Normally, an NMR spectrum plot will tell you very complex integration numbers. However, integration doesn’t have to be exact. You can just divide each integration number by the smallest number in your NMR spectrum. The ratio will help you get a big picture of the relative number of H’s represented by a peak. Combining the chemical shifts and the peak integration, you might be able to determine the structure of a molecule by using the chemical shift table. Researchers usually use NMR to check if the product they made from a reaction is what they really want. So they don’t have to figure out the structure of a molecule by looking at a complex spectrum. They know what the spectrum should look like if the reaction works. By comparing the actual spectrum to the ideal one, they are able to verify the molecule they want is in the product. Solvent used is usually CD2Cl2, since D would not show up in a H NMR spectrum. Combine with chemical shifts, they can be used to determine structure.
Proton NMR interpretation[edit | edit source]
To interpret proton NMR, it is important to know where each type of proton lies. Below is a list of types of proton and their chemical shift on NMR.
It is important to know that proton NMR peaks only indicate the presence of protons (H). It does not show other atoms like Carbon, Oxygen...etc. As mentioned in the above section, proton peaks shows spliting because of coupling by the neighbor protons. The integration of each peak is the amount of proton relative to other proton on the NMR. When solving structure from the H NMR, it is important to write down the chemical shift, integration and the split of each peak. Then base on the chemical shift of the peak, write down the possible functional group and structure. Lastly, arrange and connect each structure so that it matches the split and the integration of proton NMR. Below are examples of hand drawn proton NMR and also the detail instruction to interprete proton NMR.
Example[edit | edit source]
The interpretation of each proton NMR is given right below of each graph. Try not to look at the structure, and only look at the molecular formula and proton NMR to interpret the structure of the compound. Note that the examples given are the basic and simple compound. The NMR of protein structures is much more complex than these examples. The goal of these examples is to give you an idea how proton NMR are interpreted.
Base on the chemical shift of proton NMR, there should be a ketone functional group or a structure that contains a carbonyl group at peak around 2.0. The peak around 1.3 could be a primary or secondary alkyl group.
Now look at the splitting of the peaks at chemical shift 1.3 (C), the triplet (3 peaks) shows that the proton is probably split by 2 neighbor protons (base on the n+1 rule mention in integration section). If it is split only by 1 neighbor proton, then it would be a doublet (2 peaks). Next, look at the peak at chemical shift 2.0 (B). The singlet (single peak) means that this proton environment probably has no neighbor proton. The peak at chemical shift 4.2 (A) is a quadruplet (4 peaks). This means there are about 3 neighbor proton next to proton environment A. Since it is known that B has no proton right next to it, and A and C both has neighbor protons, it is safe to assume that proton environment A is right next to proton environment C, which could be a -CH2CH3. The following possible structures deduced above are a ketone and an ethyl group.
| Substructure | 
|

|
|---|---|---|
| Splitting pattern | Singlet | Quartet and triplet |
| Analysis | C with no neighboring H | C with three neighboring H C with two neighboring H |
Note that the there are two oxygen atoms from the molecular formula. One of the oxygen is included in ketone. The other oxygen must be binding onto one of these two structures. Take a look at peak A, the chemical shift is near 4.0, which means it might be connected to a heteroatom like oxygen. Place the oxygen next to the -CH2CH3 and connect the structure together, you will get ethyl acetate as indicated below the proton NMR. Notice that the proton B does not have any neighbor proton. Proton A is split into 4 peaks by proton C (n+1 rule, n = 3 neighbor protons). Proton C is split into 3 peaks by proton A (n = 2 neighbor protons). The CH2, secondary alkyl, base on the proton frequency table should be around the chemical shift ~1.2 ppm, but instead it is at ~4.2 ppm. The reason for this is that the CH2 is attached to oxygen a heteroatom, which is a electron withdrawing group. The result is that the chemical shift is pulled left field resulting in a chemical shift of 4.2 ppm. Another way to look at this is to assume there is an ester functional group at chemical shift of 4.2 ppm, and the primary alkyl group is attached to the ester. The integration of the proton NMR also matches the structure well. The methyl CH3 next to the carbonyl group has 3 protons, and the primary alkyl next to the CH2 has 3 protons as well. This explains why peak B has the same height as peak C (same amount of protons). Peak A has the lowest height because it only has two protons.
 This proton NMR example looks more complicated than the first one, but it is actually easier. One important information from this proton NMR is that there are peaks around 6.0~ 7.0 ppm (F,B,D,E). This always almost indicates the presence of aromatic ring. Noticed that there are about 4 group of peaks from 6.0 to 7.0 ppm? This means that there are four protons attach to 4 carbons on the aromatic ring. This leaves 2 carbons of the aromatic ring free to attach to two substituents. The position of these substituents is clearly an ortho and para position on the aromatic ring. The reason is that two different substituents on ortho and para position of the aromatic ring would give 4 proton environments. If there are only two proton environments around 6.0~ 8.0 ppm with the same integration (height), it means that the aromatic ring is probably symmetric on both sides with double para substituents. Now look at the peak (A) at 5.5 ppm. The peak is a broad peak instead of sharp peak like the rest. This means that the proton of this environment is attached to a heteroatom. The only heteroatom present in the sample base on the molecular formula given is an oxygen atom. This means that the proton is directly attached to oxygen, which would be a alcohol group -OH (Note that the proton on the alcohol group can have the chemical shift range from 0.5 to 5.0 ppm). It is important to remember that the proton that attached to a heteroatom is also known as exchangeable proton. Exchangeable proton sometimes do not show up on H NMR, so do not worry when an expected exchangeable peak doesn’t appear on HMNR.
The peak (C) at the chemical shift of ~3.9 ppm has the highest integration (height) and is a singlet. Usually when such a high singlet peak is observed around 3.9 ppm with oxygen in the molecular formula, there is a high chance that it is a ether group, -OCH3. Since there is no neighbor proton next to the CH3 of the ether, it is a singlet peak. In addition, the height of the peak is high compare to the other peak, which indicate a possibility of CH3 with at least 3 times more protons than other proton environment. Base on the interpretations above, these are the possible function groups:
This proton NMR example looks more complicated than the first one, but it is actually easier. One important information from this proton NMR is that there are peaks around 6.0~ 7.0 ppm (F,B,D,E). This always almost indicates the presence of aromatic ring. Noticed that there are about 4 group of peaks from 6.0 to 7.0 ppm? This means that there are four protons attach to 4 carbons on the aromatic ring. This leaves 2 carbons of the aromatic ring free to attach to two substituents. The position of these substituents is clearly an ortho and para position on the aromatic ring. The reason is that two different substituents on ortho and para position of the aromatic ring would give 4 proton environments. If there are only two proton environments around 6.0~ 8.0 ppm with the same integration (height), it means that the aromatic ring is probably symmetric on both sides with double para substituents. Now look at the peak (A) at 5.5 ppm. The peak is a broad peak instead of sharp peak like the rest. This means that the proton of this environment is attached to a heteroatom. The only heteroatom present in the sample base on the molecular formula given is an oxygen atom. This means that the proton is directly attached to oxygen, which would be a alcohol group -OH (Note that the proton on the alcohol group can have the chemical shift range from 0.5 to 5.0 ppm). It is important to remember that the proton that attached to a heteroatom is also known as exchangeable proton. Exchangeable proton sometimes do not show up on H NMR, so do not worry when an expected exchangeable peak doesn’t appear on HMNR.
The peak (C) at the chemical shift of ~3.9 ppm has the highest integration (height) and is a singlet. Usually when such a high singlet peak is observed around 3.9 ppm with oxygen in the molecular formula, there is a high chance that it is a ether group, -OCH3. Since there is no neighbor proton next to the CH3 of the ether, it is a singlet peak. In addition, the height of the peak is high compare to the other peak, which indicate a possibility of CH3 with at least 3 times more protons than other proton environment. Base on the interpretations above, these are the possible function groups:
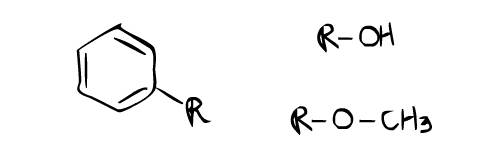
Attach the alcohol group and the ether group in ortho- para position will result in the correct structure of the compound.
Nuclear Overhauser Enhancement Spectroscopy (NOESY)[edit | edit source]

NOESY is a NMR technique that uses the Nuclear Overhauser effect to help understand the tertiary structure of proteins and other large molecules. The nuclear Overhauser effect is the interaction of nuclei at short distances from each other. The extent of the effect is approximately 5 Angstroms. This is a better analysis of tertiary structure for proteins that do not form crystalline structures and need to be analyzed in solution. Like in NMR, a magnetic field is produced around the molecule and RF waves at different frequencies are produced to produce resonance. The resonance is produced when the nucleus reverses spin. Unlike normal NMR, the aim of NOESY is to determine the effect of the resonance of one nucleus on the other nuclei in the area. The graph that is produced gives you an idea of where the nuclei are in relation to each other.
The NOESY experiment reveals the distance of protons relative to one another. Protons very close to each other, (about 3 Angstroms apart) will produce a very large signal. The limit of detection is about 5-6 Angstroms apart, and will produce only a very weak signal.
The graph has diagonal dots correspond to the placement of the nuclei on the one dimensional NMR. There are dots out side of this diagonal spectrum. These dots show what nuclei are in close proximity of each other. If a line was drawn horizontally and vertically from the outlaying dots, the dots, on the diagonal spectrum, that lay on the lines would be in close proximity to each other. Using the information from the NMR and the NOESY a tertiary structure of the macromolecules could be formed. However, the resulting tertiary structure would contain a family of structures. This happened for three reasons. The first is the approximation of the distance between the nuclei. Second, there may not have been enough constraints to produce a singular structure. Thirdly, the protein is in solution, and the solution contains many proteins.
This technique is mainly used for hydrogen atoms, because they are the most abundant atom in biological systems and are also the simplest.
Protein NMR[edit | edit source]
An NMR machine is essentially a huge magnet. Many atoms are essentially little magnets. When placed inside an NMR machine, all the little magnets orient themselves to line up with the big magnet. By harnessing this law of physics, NMR spectroscopists are able to figure out physical, chemical, electronic, and structural information about molecules.
NMR relies on the interaction between an applied magnetic field and the natural “little magnets” in certain atomic nuclei. For protein structure determination, spectroscopists concentrate on the atoms that are most common in proteins: hydrogen, carbon, and nitrogen. What researchers seek to learn through NMR is how this chain of amino acids wraps and folds around itself to create the three-dimensional, active protein. Solving a protein structure using NMR is a series of experiments, each of which provides partial clues about the nature of the atoms in the sample molecule, such as how close two atoms are to each other, whether these atoms are physically bonded to each other, or where the atoms lie within the same amino acid. Other experiments show links between adjacent amino acids or reveal flexible regions in the protein. Each new set of experiments further refines possible structures until finally the scientists carefully select 10 to 20 solution that best represent their data and present the average as their final structure.
Sample Preparation for NMR
In order to study protein structure by NMR, highly purified samples of the protein of interest must be prepared. The protein can either be isolated from natural sources, or expressed in host organisms such as E. Coli through recombinant DNA techniques. The bacteria with the recombinant gene coding for a specific protein are grown in minimal media with 15NH4Cl being the only source of nitrogen for the bacteria, and 13C-glucose offering the only source of carbon for the bacteria to make proteins. This way, when the bacteria produce the protein of interest, these proteins are labeled with 15N and 13C, both of which are NMR active. The protein of interest is then purified through various protein purification techniques (See protein purification techniques). Finally, the protein, in an appropriate buffer, is loaded into an NMR tube and is ready to be placed in the NMR magnet.

NMR Experiments
2D ExperimentsThere are many different types of NMR experiments one can run to help to reveal information about the structure of the protein. The experiments usually differ in what correlations are detected. For example, a 2D [1H-1H]-NOESY experiment will reveal hydrogen atoms that are within 0.5 nm apart. Protons that exhibit this interaction will show up as a cross peak on the 2D spectrum (Figure 2).

Taking this information, theoretically, the protons at 8 ppm and 9 ppm on the 1D spectrum could be assigned to a certain residue in the amino acid sequence. For example, if Ala1 is the point at 8 ppm and Ala54 is at 9 ppm, and there is a crosspeak present, then the observation of this NOE reveals a circular structure for this polypeptide chain (Figure 3).

Because proteins are much more complicated than this example above, the 2D NOESY spectrum is often cluttered and crosspeaks cannot be made out clearly because many of these points may stack on top of one another. Other experiments are required to reveal the necessary information to determine the 3D structure of the protein, such as 3D experiments.
3D Experiments 3D experiments use a third dimension to reveal peaks that may be stacked on top of one another in the 2D spectrum. An example is 3D 15N-correlated [1H-1H]-NOESY (Figure 4). There are many other experiments to correlate different nuclei and their neighbors.

Protein NMR Advantages[edit | edit source]
NMR is a good method in trying to solve the structure of a protein and the continued unanswered protein folding problem. However it is not the only method as crystallography is also a possible method for determining protein structure. However, NMR has its advantages over crystallography.
One instance is that it uses molecules in solution, so it is not limited to those that crystallize well since crystallization is a very uncertain and time-consuming step in X-ray crystallography. In addition, some proteins do not readily crystallize. Furthermore, although structures present in crystallized proteins very closely represent those of proteins free of the constraints imposed by the crystalline environment, structures in solution can be sources of additional insights. NMR also makes it fairly easy to study properties of a molecule besides its structure such as the flexibility of the molecule and how it interacts with other molecules. With crystallography, it is either impossible to study these aspects or it requires an entirely new crystal.
Protein NMR Disadvantages[edit | edit source]
Most NMR spectroscopists focus on molecules no larger than 20-30 kilodaltons. X-ray crystallographers have solved structures upto 2,500 kilodaltons.
NMR in Real Life[edit | edit source]
The 15 carbon compound viniferone found in grape seeds was isolated in 2004. Viniferone falls into a group of substances, grape seed, that are very active against radicals and oxidative stress. There was very little recovery of viniferone from an abundance of grape seeds (~40 mg of viniferone from 10.5 kg of grape seeds), so precautions had to be taken in the techniques used to obtain its structure. Most tests would destroy the minuscule amount proanthocyanidins t of viniferone obtained, so a combination of spectroscopic techniques were utilized (including NMR) to obtain viniferone's structure. Obtaining the 1H and 13C NMR data was critical in determining the structure of Viniferone. The variety of absorption signals at various chemical shifts helped determine the presence of alkenes and benzene rings. Correlation spectroscopy and eventually X-ray crystallography were used to verify the structural arrangement of Viniferone.[1]
References[edit | edit source]
- ↑ Schore, Neil E. (2011). Organic Chemistry Structure and Function 6th Edition. W. H. Freeman
If you would like to learn more about interpreting NMR peaks, I highly suggest this website. http://www.wfu.edu/~ylwong/chem/nmr/h1/
Berg, Jeremy M., Lubert Stryer, and John L. Tymoczko. Biochemistry. 6th ed. Boston: W. H. Freeman & Company, 2006. 98-101.
Shriner, Christine K. F. Hermann, Terence C. Morrill, David Y. Curtin, Reynold C. Fuson. The Systematic Identification of Organic Compounds. 8th ed. U.S.A. John Wiley & Sons, Inc. 2004. 136-142.
Vollhardt, K. Peter C., Schore, Neil E. Organic Chemistry - Structure and Function. 5th ed. New York: W. H. Freeman & Company, 2005. 398-432.
Keeler, James. Understanding NMR Spectroscopy. West Sussex, England. John Wiley & Sons. 51-77.
Clore, Marius G., Gronenborn, Angela M. “Chapter 34: Structures of Larger Proteins, Protein-Ligand, and Protein-DNA Complexes by Multidimensional Heteronuclear NMR.” Multidimensional NMR Methods for the Solution State. United Kingdom. John Wiley & Sons Ltd.
Wuthrich, Kurt. “Chapter 33: Biological Macromolecules: Structure Determination in Solution.” Multidimensional NMR Methods for the Solution State. United Kingdom. John Wiley & Sons Ltd.
National Institutes of Health, National Institute of General Medical Sciences, New York, 2007, 29-30, http://www.nigms.nih.gov.
[1]"Kurt Wüthrich - Nobel Lecture". Nobelprize.org. 25 Oct 2010 http://nobelprize.org/nobel_prizes/chemistry/laureates/2002/wuthrich-lecture.html

