Statistics/Numerical Methods/Optimization
Introduction[edit | edit source]
In the following we will provide some notes on numerical optimization algorithms. As there are numerous methods out there, we will restrict ourselves to the so-called Gradient Methods. There are basically two arguments why we consider this class as a natural starting point when thinking about numerical optimization algorithms. On the one hand, these methods are really workhorses in the field, so their frequent use in practice justifies their coverage here. On the other hand, this approach is highly intuitive in the sense that it somewhat follow naturally from the well-known properties of optima. In particular we will concentrate on three examples of this class: the Newtonian Method, the Method of Steepest Descent and the class of Variable Metric Methods, nesting amongst others the Quasi Newtonian Method.
Before we start we will nevertheless stress that there does not seem to be a "one and only" algorithm but the performance of specific algorithms is always contingent on the specific problem to be solved. Therefore both experience and "trial-and-error" are very important in applied work. To clarify this point we will provide a couple of applications where the performance of different algorithms can be compared graphically. Furthermore a specific example on Maximum Likelihood Estimation can be found at the end. Especially for statisticians and econometricians the Maximum Likelihood Estimator is probably the most important example of having to rely on numerical optimization algorithms in practice.
Theoretical Motivation[edit | edit source]
Any numerical optimization algorithm has solve the problem of finding "observable" properties of the function such that the computer program knows that a solution is reached. As we are dealing with problems of optimization two well-known results seem to be sensible starting points for such properties.
If f is differentiable and is a (local) minimum, then
i.e. the Jacobian is equal to zero
and
If f is twice differentiable and is a (local) minimum, then
i.e. the Hessian is pos. semidefinite.
In the following we will always denote the minimum by . Although these two conditions seem to represent statements that help in finding the optimum , there is the little catch that they give the implications of being an optimum for the function . But for our purposes we would need the opposite implication, i.e. finally we want to arrive at a statement of the form: "If some condition is true, then is a minimum". But the two conditions above are clearly not sufficient in achieving this (consider for example the case of , with but ). Hence we have to look at an entire neighborhood of as laid out in the following sufficient condition for detecting optima:
If and and , then: is a local minimum.
Proof: For let . The Taylor approximation yields: , where denotes an open ball around , i.e. for .
In contrast to the two conditions above, this condition is sufficient for detecting optima - consider the two trivial examples
with but
and
with and .
Keeping this little caveat in mind we can now turn to the numerical optimization procedures.
Numerical Solutions[edit | edit source]
All the following algorithms will rely on the following assumption:
(A1) The set is compact
where is some given starting value for the algorithm. The significance of this assumption has to be seen in the Weierstrass Theorem which states that every compact set contains its supremum and its infimum. So (A1) ensures that there is some solution in . And at this global minimum it of course holds true that . So - keeping the discussion above in mind - the optimization problem basically boils down to the question of solving set of equations .
The Direction of Descent[edit | edit source]
The problems with this approach are of course rather generically as does hold true for maxima and saddle points as well. Hence, good algorithms should ensure that both maxima and saddle points are ruled out as potential solutions. Maxima can be ruled out very easily by requiring i.e. we restrict ourselves to a sequence such that the function value decreases in every step. The question is of course if this is always possible. Fortunately it is. The basic insight why this is the case is the following. When constructing the mapping (i.e. the rule how we get from to ) we have two degrees of freedoms, namely
- the direction and
- the step length .
Hence we can choose in which direction we want to move to arrive at and how far this movement has to be. So if we choose and in the "right way" we can effectively ensure that the function value decreases. The formal representation of this reasoning is provided in the following
Lemma: If and then: such that
Proof: As and , it follows that for small enough.
The General Procedure of Descending Methods[edit | edit source]
A direction vector that satisfies this condition is is called a Direction of Descent. In practice this Lemma allows us to use the following procedure to numerically solve optimization problems.
1. Define the sequence recursively via
2. Choose the direction from local information at the point
3. Choose a step size that ensures convergence of the algorithm.
4. Stop the iteration if where is some chosen tolerance value for the minimum
This procedure already hints that the choice of and are not separable, but rather dependent. Especially note that even if the method is a descending method (i.e. both and are chosen according to Lemma 1) the convergence to the minimum is not guaranteed. At a first glance this may seem a bit puzzling. If we found a sequence such that the function value decreases at every step, one might think that at some stage, i.e. in the limit of k tending to infinity we should reach the solution. Why this is not the case can be seen from the following example borrowed from W. Alt (2002, p. 76).
Example 1[edit | edit source]
- Consider the following example which does not converge although it is clearly descending. Let the criterion function be given by
, let the starting value be , consider a (constant) direction vector and choose a step width of . Hence the recursive definition of the sequence follows as
Note that and hence , so that it is clearly a descending method. Nevertheless we find that
The reason for this non-convergence has to be seen in the stepsize decreasing too fast. For large k the steps get so small that convergence is precluded. Hence we have to link the stepsize to the direction of descend .
Efficient Stepsizes[edit | edit source]
The obvious idea of such a linkage is to require that the actual descent is proportional to a first order approximation, i.e. to choose such that there is a constant such that
Note that we still look only at descending directions, so that as required in Lemma 1 above. Hence, the compactness of implies the convergence of the LHS and by (4)
Finally we want to choose a sequence such that because that is exactly the necessary first order condition we want to solve. Under which conditions does (5) in fact imply ? First of all the stepsize must not go to zero too quickly. That is exactly the case we had in the example above. Hence it seems sensible to bound the stepsize from below by requiring that
for some constant . Substituting (6) into (5) finally yields
where again the compactness of ensures the convergence of the LHS and hence
Stepsizes that satisfy (4) and (6) are called efficient stepsizes and will be denoted by . The importance of condition (6) is illustrated in the following continuation of Example 1.
Example 1 (continued)[edit | edit source]
- Note that it is exactly the failure of (6) that induced Example 1 not to converge. Substituting the stepsize of the example into (6) yields
so there is no constant satisfying this inequality for all k as required in (6). Hence the stepsize is not bounded from below and decreases too fast. To really acknowledge the importance of (6), let us change the example a bit and assume that . Then we find that
i.e. convergence actually does take place. Furthermore recognize that this example actually does satisfy condition (6) as
Choosing the Direction d[edit | edit source]
We have already argued that the choice of and is intertwined. Hence the choice of the "right" is always contingent on the respective stepsize . So what does "right" mean in this context? Above we showed in equation (8) that choosing an efficient stepsize implied
The "right" direction vector will therefore guarantee that (8') implies that
as (9) is the condition for the chosen sequence to converge. So let us explore what directions could be chosen to yield (9). Assume that the stepsize is efficient and define
By (8') and (10) we know that
So if we bound from below (i.e. ), (11) implies that
where (12) gives just the condition of the sequence converging to the solution . As (10) defines the direction vector implicitly by , the requirements on translate directly into requirements on .
Why Gradient Methods?[edit | edit source]
When considering the conditions on it is clear where the term Gradient Methods originates from. With given by
we have the following result
Given that was chosen efficiently and satisfies
we have
Hence: Convergence takes place if the angle between the negative gradient at and the direction is consistently smaller than the right angle. Methods relying on satisfying (13) are called Gradient Methods.
In other words: As long as one is not moving orthogonal to the gradient and if the stepsize is chosen efficiently, Gradient Methods guarantee convergence to the solution .
Some Specific Algorithms in the Class of Gradient Methods[edit | edit source]
Let us now explore three specific algorithms of this class that differ in their respective choice of .
The Newtonian Method[edit | edit source]
The Newtonian Method is by far the most popular method in the field. It is a well known method to solve for the roots of all types of equations and hence can be easily applied to optimization problems as well. The main idea of the Newtonian method is to linearize the system of equations to arrive at
(15) can easily be solved for x as the solution is just given by (assuming to be non-singular)
For our purposes we just choose to be the gradient and arrive at
where is the so-called Newtonian Direction.
Properties of the Newtonian Method[edit | edit source]
Analyzing (17) elicits the main properties of the Newtonian method:
- If is positive definite, is a direction of descent in the sense of Lemma 1.
- The Newtonian Method uses local information of the first and second derivative to calculate .
- As
the Newtonian Method uses a fixed stepsize of . Hence the Newtonian method is not necessarily a descending method in the sense of Lemma 1. The reason is that the fixed stepsize might be larger than the critical stepsize given in Lemma 1. Below we provide the Rosenbrock function as an example where the Newtonian Method is not descending.
- The Method can be time-consuming as calculating for every step k can be cumbersome. In applied work one could think about approximations. One could for example update the Hessian only every sth step or one could rely on local approximations. This is known as the Quasi-Newtonian-Method and will be discussed in the section about Variable Metric Methods.
- To ensure the method to be decreasing one could use an efficient stepsize and set
Method of Steepest Descent[edit | edit source]
Another frequently used method is the Method of Steepest Descent. The idea of this method is to choose the direction so that the decrease in the function value f is maximal. Although this procedure seems at a first glance very sensible, it suffers from the fact that it uses effectively less information than the Newtonian Method by ignoring the Hessian's information about the curvature of the function. Especially in the applications below we will see a couple of examples of this problem.
The direction vector of the Method of Steepest Descent is given by
Proof: By the Cauchy-Schwartz Inequality it follows that
Obviously (21) holds with equality for given in (20).
Note especially that for we have , i.e. we just "walk" in the direction of the negative gradient. In contrast to the Newtonian Method the Method of Steepest Descent does not use a fixed stepsize but chooses an efficient stepsize . Hence the Method of Steepest Descent defines the sequence by
where is an efficient stepsize and the Direction of Steepest Descent given in (20).
Properties of the Method of Steepest Descent[edit | edit source]
- With the Method of Steepest Descent defines a direction of descent in the sense of Lemma 1, as
- The Method of Steepest Descent is only locally sensible as it ignores second order information.
- Especially when the criterion function is flat (i.e. the solution lies in a "valley") the sequence defined by the Method of Steepest Descent fluctuates wildly (see the applications below, especially the example of the Rosenbrock function).
- As it does not need the Hessian, calculation and implementation of the Method of Steepest Descent is easy and fast.
Variable Metric Methods[edit | edit source]
A more general approach than both the Newtonian Method and the Method of Steepest Descent is the class of Variable Metric Methods. Methods in this class rely on the updating formula
If is a symmetric and positive definite matrix, (23) defines a descending method as is positive definite if and only if is positive definite as well. To see this: just consider the spectral decomposition
where and are the matrices with eigenvectors and eigenvalues respectively. If is positive definite, all eigenvalues are strictly positive. Hence their inverse are positive as well, so that is clearly positive definite. But then, substitution of yields
i.e. the method is indeed descending. Up to now we have not specified the matrix , but is easily seen that for two specific choices, the Variable Metric Method just coincides with the Method of Steepest Descent and the Newtonian Method respectively.
- For (with being the identity matrix) it follows that
which is just the Method of Steepest Descent.
- For it follows that
which is just the Newtonian Method using a stepsize .
The Quasi Newtonian Method[edit | edit source]
A further natural candidate for a Variable Metric Method is the Quasi Newtonian Method. In contrast to the standard Newtonian Method it uses an efficient stepsize so that it is a descending method and in contrast to the Method of Steepest Descent it does not fully ignore the local information about the curvature of the function. Hence the Quasi Newtonian Method is defined by the two requirements on the matrix :
- should approximate the Hessian to make use of the information about the curvature and
- the update should be easy so that the algorithm is still relatively fast (even in high dimensions).
To ensure the first requirement, should satisfy the so-called Quasi-Newtonian-Equation
as all satisfying (26) reflect information about the Hessian. To see this, consider the function defined as
Then it is obvious that and . So and are reasonably similar in the neighborhood of . In order to ensure that is also a good approximation at , we want to choose such that the gradients at are identical. With
it is clear that if satisfies the Quasi Newtonian Equation given in (26). But then it follows that
Hence as long as and are not too far apart, satisfying (26) is a good approximation of .
Let us now come to the second requirement that the update of the should be easy. One specific algorithm to do so is the so-called BFGS-Algorithm. The main merit of this algorithm is the fact that it uses only the already calculated elements and to construct the update . Hence no new entities have to be calculated but one has only to keep track of the x-sequence and sequence of gradients. As a starting point for the BFGS-Algorithm one can provide any positive definite matrix (e.g. the identity matrix or the Hessian at ). The BFGS-Updating-Formula is then given by
where and . Furthermore (30) ensures that all are positive definite as required by Variable Metric Methods to be descending.
Properties of the Quasi Newtonian Method[edit | edit source]
- It uses second order information about the curvature of as the matrices are related to the Hessian .
- Nevertheless it ensures easy and fast updating (e.g. by the BFGS-Algorithm) so that it is faster than the standard Newtonian Method.
- It is a descending method as are positive definite.
- It is relatively easy to implement as the BFGS-Algorithm is available in most numerical or statistical software packages.
Applications[edit | edit source]
To compare the methods and to illustrate the differences between the algorithms we will now evaluate the performance of the Steepest Descent Method, the standard Newtonian Method and the Quasi Newtonian Method with an efficient stepsize. We use two classical functions in this field, namely the Himmelblau and the Rosenbrock function.
Application I: The Himmelblau Function[edit | edit source]
The Himmelblau function is given by
This fourth order polynomial has four minima, four saddle points and one maximum so there are enough possibilities for the algorithms to fail. In the following pictures we display the contour plot and the 3D plot of the function for different starting values.
In Figure 1 we display the function and the paths of all three methods at a starting value of . Obviously the three methods do not find the same minimum. The reason is of course the different direction vector of the Method of Steepest Descent - by ignoring the information about the curvature it chooses a totally different direction than the two Newtonian Methods (see especially the right panel of Figure 1).
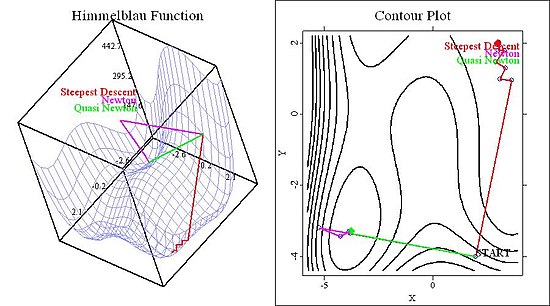
Consider now the starting value , displayed in Figure 2. The most important thing is of course that now all methods find different solutions. That the Method of Steepest Descent finds a different solution than the two Newtonian Methods is again not that surprising. But that the two Newtonian Methods converge to different solution shows the significance of the stepsize . With the Quasi-Newtonian Method choosing an efficient stepsize in the first iteration, both methods have different stepsizes and direction vectors for all iterations after the first one. And as seen in the picture: the consequence may be quite significant.

Application II: The Rosenbrock Function[edit | edit source]
The Rosenbrock function is given by
Although this function has only one minimum it is an interesting function for optimization problems. The reason is the very flat valley of this U-shaped function (see the right panels of Figures 3 and 4). Especially for econometricians this function may be interesting because in the case of Maximum Likelihood estimation flat criterion functions occur quite frequently. Hence the results displayed in Figures 3 and 4 below seem to be rather generic for functions sharing this problem.
My experience when working with this function and the algorithms I employed is that Figure 3 (given a starting value of ) seems to be quite characteristic. In contrast to the Himmelblau function above, all algorithms found the same solution and given that there is only one minimum this could be expected. More important is the path the different methods choose as is reflects the different properties of the respective methods. It is seen that the Method of Steepest Descent fluctuates rather wildly. This is due to the fact that it does not use information about the curvature but rather jumps back and forth between the "hills" adjoining the valley. The two Newtonian Methods choose a more direct path as they use the second order information. The main difference between the two Newtonian Methods is of course the stepsize. Figure 3 shows that the Quasi Newtonian Method uses very small stepsizes when working itself through the valley. In contrast, the stepsize of the Newtonian Method is fixed so that it jumps directly in the direction of the solution. Although one might conclude that this is a disadvantage of the Quasi Newtonian Method, note of course that in general these smaller stepsizes come with benefit of a higher stability, i.e. the algorithm is less likely to jump to a different solution. This can be seen in Figure 4.

Figure 4, which considers a starting value of , shows the main problem of the Newtonian Method using a fixed stepsize - the method might "overshoot" in that it is not descending. In the first step, the Newtonian Method (displayed as the purple line in the figure) jumps out of the valley to only bounce back in the next iteration. In this case convergence to the minimum still occurs as the gradient at each side points towards the single valley in the center, but one can easily imagine functions where this is not the case. The reason of this jump are the second derivatives which are very small so that the step gets very large due to the inverse of the Hessian. In my experience I would therefore recommend to use efficient stepsizes to have more control over the paths the respective Method chooses.

Application III: Maximum Likelihood Estimation[edit | edit source]
For econometricians and statisticians the Maximum Likelihood Estimator is probably the most important application of numerical optimization algorithms. Therefore we will briefly show how the estimation procedure fits in the framework developed above.
As usual let
be the conditional density of given with parameter and
the conditional likelihood function for the parameter
If we assume the data to be independently, identically distributed (iid) then the sample log-likelihood follows as
Maximum Likelihood estimation therefore boils down to maximize (35) with respect to the parameter . If we for simplicity just decide to use the Newtonian Method to solve that problem, the sequence is recursively defined by
where and denotes the first and second derivative with respect to the parameter vector and defines the Newtonian Direction given in (17). As Maximum Likelihood estimation always assumes that the conditional density (i.e. the distribution of the error term) is known up to the parameter , the methods described above can readily be applied.
A Concrete Example of Maximum Likelihood Estimation[edit | edit source]
Assume a simple linear model
with . The conditional distribution Y is then determined by the one of U, i.e.
where denotes the density function. Generally, there is no closed form solution of maximizing (35) (at least if U does not happen to be normally distributed), so that numerical methods have to be employed. Hence assume that U follows Student's t-distribution with m degrees of freedom so that (35) is given by
where we just used the definition of the density function of the t-distribution. (38) can be simplified to
so that (if we assume that the degrees of freedom m are known)
With the criterion function
the methods above can readily applied to calculate the Maximum Likelihood Estimator maximizing (41).
References[edit | edit source]
- Alt, W. (2002): "Nichtlineare Optimierung", Vieweg: Braunschweig/Wiesbaden
- Härdle, W. and Simar, L. (2003): "Applied Multivariate Statistical Analysis", Springer: Berlin Heidelberg
- Königsberger, K. (2004): "Analysis I", Springer: Berlin Heidelberg
- Ruud, P. (2000): "Classical Econometric Theory", Oxford University Press: New York
















































































![{\displaystyle (16)\quad x={\hat {x}}-[Dg({\hat {x}})^{T}]^{-1}g({\hat {x}}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/973ad4b1a68c0301124de9a8e4a9f5dcf2ede103)

![{\displaystyle (17)\quad d_{N}^{(k)}=x^{(k+1)}-x^{(k)}=-[D^{2}f(x^{(k)})]^{-1}Df(x^{(k)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78f590fdfab4360315b24683a209d394d474d8d5)






![{\displaystyle [D^{2}f(x^{(k)})]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18f24df6687d0360e41c29464f4aaf177e9314f9)
![{\displaystyle (19)\quad x^{(k+1)}=x^{(k)}-\sigma _{E}^{(k)}d_{N}^{(k)}=x^{(k)}-\sigma _{E}^{(k)}[D^{2}f(x^{k})]^{-1}Df(x^{(k)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e7b82c56b6571dc71773a1301041f3e514bb0be)









![{\displaystyle (23)\quad x^{k+1}=x^{k}-\sigma _{E}^{(k)}[A^{k}]^{-1}Df(x^{k}).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8b5580a0328e0fc4cb23c05d2aaa2dfb757e774)

![{\displaystyle [A^{k}]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6caa38bd6a32cf081b1e8379b42ccafdeaf56056)





![{\displaystyle [A^{k}]^{-1}=\Gamma \Lambda ^{-1}\Gamma ^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0bb61f96e4008fe7ac42ddae42174a1cbc74f22)
![{\displaystyle d^{(k)}=[A^{k}]^{-1}Df(x^{k})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2dd88606c2704c7ca9ba41fbff98dc6196d731f1)
![{\displaystyle (25)\quad Df(x^{k})^{T}d^{(k)}=-Df(x^{k})^{T}[A^{k}]^{-1}Df(x^{k})\equiv -v^{T}[A^{k}]^{-1}v\leq 0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19c3cfc50845559d027b7a787662c23b8209bdba)




![{\displaystyle (19')\quad x^{k+1}=x^{k}-\sigma _{E}^{(k)}[D^{2}f(x^{k})]^{-1}Df(x^{k})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e585e07182f56dfbe1ebb268e5b1feba19cac6e)























![{\displaystyle [Df(x^{(k)})]^{-1}Df(x^{(k)}))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60231e722c13de70156e005a9956e01b4895cda1)







![{\displaystyle (36)\quad D_{\theta }{\mathcal {L}}(\theta ^{(k+1)})=D_{\theta }{\mathcal {L}}(\theta ^{(k)})+D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})(\theta ^{(k+1)}-\theta ^{(k)})=0\Leftrightarrow \theta ^{(k+1)}=\theta ^{(k)}-[D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})]^{-1}D_{\theta }{\mathcal {L}}(\theta ^{(k)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27be895a860dcd9530a4d300fdc8fa7f7e7f9e3c)


![{\displaystyle [D_{\theta \theta }{\mathcal {L}}(\theta ^{(k)})]^{-1}D_{\theta }{\mathcal {L}}(\theta ^{(k)})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1bb702f696e4c7c16d636cdafdbf51382f32bfd)





![{\displaystyle (39)\quad {\mathcal {L}}(\theta ;Y_{\mid X})=N\left[\log \left(\Gamma \left({\frac {m+1}{2}}\right)\right)-\log \left({\sqrt {\pi m}}\Gamma \left({\frac {m}{2}}\right)\right)\right]-{\frac {m+1}{2}}\sum \log \left(1+{\frac {(y_{i}-x_{i}^{T}\beta )^{2}}{m}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56ab57a856625145f8bd9be4f656dba107baf35a)


