Signals and Systems/Frequency Response

From Wikibooks, the open-content textbooks collection

Jump to: navigation, search
Signals and Systems

Contents

[edit] Frequency Response

Systems respond differently to inputs of different frequencies. Some systems may amplify components of certain frequencies, and attenuate components of other frequencies. The way that the system output is related to the system input for different frequencies is called the frequency response of the system.

The frequency response, sometimes called the "Frequency Response Function" (FRF) is the relationship between the system input and output in the Fourier Domain.


Fourier Transfer Block.svg


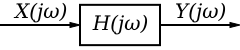
In this system, X(jω) is the system input, Y(jω) is the system output, and H(jω) is the frequency response. We can define the relationship between these functions as:

Y(jω) = H(jω)X(jω)
\frac{Y(j\omega)}{X(j\omega)} = H(j\omega)

[edit] The Frequency Response Functions

Since the frequency response is a complex function, we can convert it to polar notation in the complex plane. This will give us a magnitude and an angle. We call the angle the "phase". For each frequency, the magnitude represents the system's tendency to amplify or attenuate the input signal. The phase represents the system's tendency to modify the phase of the input sinusoids. We define these two quantities as:

\left| {H\left( {j\omega } \right)} \right| = A\left( \omega \right)
\angle H\left( {j\omega } \right) = \phi \left( \omega \right).

We call A(ω) the amplitude response function (ARF) or simply the "Amplitude Response". We call φ(ω) the phase response function (PRF) or the "Phase Response".

[edit] Example: Electric Circuit

Consider the following general circuit with phasor input and output voltages:

General Filter Circuit.svg

Where

V_o \left( {j\omega } \right) = V_{om} \cos \left( {\omega t + \theta_i } \right)=V_{om} \angle \theta _o
V_i \left( {j\omega } \right) = V_{im} \cos \left( {\omega t + \theta_o } \right)=V_{im} \angle \theta _i

As before, we can define the system function, H(jω) of this circuit as:

H\left( {j\omega } \right) = {{V_o \left( {j\omega } \right)} \over {V_i \left( {j\omega } \right)}}
A\left( \omega \right) = \left| {H\left( {j\omega } \right)} \right| = {{\left| {V_o \left( {j\omega } \right)} \right|} \over {\left| {V_i \left( {j\omega } \right)} \right|}} = {{V_{om} } \over {V_{im} }}
\phi \left( \omega \right) = \angle H\left( {j\omega } \right) = \angle \left( {{{V_o \left( {j\omega } \right)} \over {V_i \left( {j\omega } \right)}}} \right) = \angle V_o \left( {j\omega } \right) - \angle V_i \left( {j\omega } \right) = \theta _o - \theta _i

Rearranging gives us the following transformations:

V_{om}=A \left( \omega \right) V_{im}
\theta_o=\theta_i + \phi \left( \omega \right)

[edit] Example: Low-Pass Filter

We will illustrate this method using a simple low-pass filter with general values as an example. This kind of circuit allows low frequencies to pass, but blocks higher ones. We will discuss filters in more detail in a later chapter.

Find the frequency response function, and hence the amplitude and phase response functions, of the following general circuit (it is already in phasor form):

1st Order Lowpass Filter (Phasor).svg

Firstly, the we use the voltage divider rule to get the output phasor in terms on the input phasor:

V_o \left( {j\omega } \right) = V_i \left( {j\omega } \right) \cdot {{{1 \over {j\omega C}}} \over {R + {1 \over {j\omega C}}}}

Now we can easily determine the FRF:

H\left( {j\omega } \right) = {{V_o \left( {j\omega } \right)} \over {V_i \left( {j\omega } \right)}} = {{{1 \over {j\omega C}}} \over {R + {1 \over {j\omega C}}}}

This simiplifies down to:

>H\left( {j\omega } \right) = {1 \over {1 + j\omega RC}}

This is the FRF. From here we can find the ARF amd PRF:

A\left( \omega \right) = \left| {H\left( {j\omega } \right)} \right| = {1 \over {\sqrt {1 + \left( {\omega CR} \right)^2 } }}
\phi \left( \omega \right) = \angle H\left( {j\omega } \right) = \tan ^{ - 1} \left( {{0 \over 1}} \right) - \tan ^{ - 1} \left( {{{\omega RC} \over 1}} \right) = - \tan ^{ - 1} \left( {\omega RC} \right)

We can plot the graphs of the ARF and PRF to get a proper idea of the FRF:

1st Order Lowpass Filter ARF Lin.svg
1st Order Lowpass Filter PRF Lin.svg

It is often easier to interpret the graphs when they are plotted on suitable logarithmic scales:

1st Order Lowpass Filter ARF Log.svg
1st Order Lowpass Filter PRF Log.svg

This shows that the circuit is indeed a filter that removes higher frequencies. Such a filter is called a lowpass filter.

The ARF and PRF of an arbitrary circuit can be plotted using an instrument called a spectrum analyser or gain and phase test set. See Practical Electronics for more details on using these instruments.

[edit] Frequency Transformations

[edit] Filters

An important concept to take away from these examples is that by desiging a proper system called a filter, we can selectively attenuate or amplify certain frequency ranges. This means that we can minimize certain unwanted frequency components (such as noise or competing data signals), and maximize our own data data signal

We can define a "received signal" r as a combination of a data signal d and unwanted components v:

r(t) = d(t) + v(t)

We can take the energy spectral density of r to determine the frequency ranges of our data signal d. We can design a filter that will attempt to amplify these frequency ranges, and attenuate the frequency ranges of v. We will discuss this problem and filters in general in the next few chapters. More advanced discussions of this topic will be in the book on Signal Processing.

Retrieved from "http://en.wikibooks.org/wiki/Signals_and_Systems/Frequency_Response"