Practical Electronics/Operating amplifiers

Intro

Op Amp is a short hand term for Operational Amplifier. An operational amplifier is a circuit component that amplifies the difference of two input voltages:

V_o = A (V₂ - V₁)

Op Amps are usually packaged as an 8-pin integrated circuit.

Operational Amplifier IC Chip

Pin	Usage
1	Offset Null
2	Inverted Input
3	Non-Inverted Input
4	-V Supply
5	No use
6	Output
7	+V Supply
8	No use

Op Amp symbol

• V₊: non-inverting input
• V₋: inverting input
• V_out: output
• V_S+: positive power supply
• V_S−: negative power supply

Op amps amplify AC signal or AC Voltage better than a simple bipolar junction transistor.

Op Amp Functions

Voltage Difference Amplifier

From above

V₀ = A (V₂ - V₁)

Voltage Comparator

V₂ > V₁ , V₀ = +V_ss

V₂ < V₁ , V₀ = -V_ss

V₂ = V₁ , V₀ = 0

Inverting Amplifier

With one voltage is grounded

If V₂ = 0 , V₀ = -A V₁ . Inverting Amplifier

Non-Inverting Amplifier

With one voltage is grounded

If V₁ = 0 , V₀ = A V₂ . Non-Inverting Amplifier

Linear Configurations

Differential amplifier

Differential amplifier

$V_\mathrm{out} = V_2 \left( { \left( R_\mathrm{f} + R_1 \right) R_\mathrm{g} \over \left( R_\mathrm{g} + R_2 \right) R_1} \right) - V_1 \left( {R_\mathrm{f} \over R_1} \right)$

• Differential $Z_\mathrm{in}$ (between the two input pins) = $R_1 + R_2$

Voltage Difference Amplifier

Whenever $R_1 = R_2$ and $R_\mathrm{f} = R_\mathrm{g}$,

$V_\mathrm{out} = {R_\mathrm{f} \over R_1} \left( V_2 - V_1 \right)$

Voltage Difference

When $R_1 = R_\mathrm{f}$ and $R_2 = R_\mathrm{g}$ (including previous conditions, so that $R_1 = R_2 = R_\mathrm{f} = R_\mathrm{g}$):

$V_\mathrm{out} = V_2 - V_1 \,\!$

Inverting Amplifier

Inverting amplifier

$V_\mathrm{out} = - V_\mathrm{in} \left( {R_f \over R_1} \right)$

Inverting Amplification is dictated by the ratio of the two resistors

Non-Inverting Amplifier

Non-inverting amplifier

$V_\mathrm{out} = V_\mathrm{in} \left( 1 + {R_2 \over R_1} \right)$

Non-Inverting Amplification is dictated by the ratio of the two resistors plus one

Voltage Follower

Voltage follower

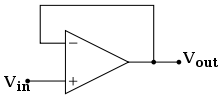
From Non-Inverting Amplifier's formula. If the resistors has the same value of resistance then output voltage is exactly equal to the input voltage

$V_\mathrm{out} = V_\mathrm{in} \!\$

From Inverting Amplifier's formula. If the resistors has the same value of resistance then output voltage is exactly equal to the input voltage and inverted

$V_\mathrm{out} = - V_\mathrm{in} \!\$

Summing amplifier

Summing amplifier

$V_\mathrm{out} = - R_\mathrm{f} \left( { V_1 \over R_1 } + { V_2 \over R_2 } + \cdots + {V_n \over R_n} \right)$

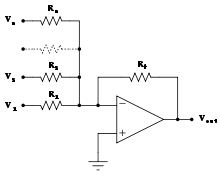
When $R_1 = R_2 = \cdots = R_n$, and $R_\mathrm{f}$ independent

$V_\mathrm{out} = - \left( {R_\mathrm{f} \over R_1} \right) (V_1 + V_2 + \cdots + V_n ) \!\$

When $R_1 = R_2 = \cdots = R_n = R_\mathrm{f}$

$V_\mathrm{out} = - ( V_1 + V_2 + \cdots + V_n ) \!\$

Integrator

Integrating amplifier

Integrates the (inverted) signal over time

$V_\mathrm{out} = \int_0^t - {V_\mathrm{in} \over RC} \, dt + V_\mathrm{initial}$

(where $V_\mathrm{in}$ and $V_\mathrm{out}$ are functions of time, $V_\mathrm{initial}$ is the output voltage of the integrator at time t = 0.)

Differentiator

Differentiating amplifier

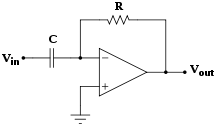
Differentiates the (inverted) signal over time.

The name "differentiator" should not be confused with the "differential amplifier", also shown on this page.

$V_\mathrm{out} = - RC \left( {dV_\mathrm{in} \over dt} \right)$

(where $V_\mathrm{in}$ and $V_\mathrm{out}$ are functions of time)

Comparator

Comparator

• $V_\mathrm{out} = \left\{\begin{matrix} V_\mathrm{S+} & V_1 > V_2 \\ V_\mathrm{S-} & V_1 < V_2 \end{matrix}\right.$

Từ V₀ = A (V₂ - V₁)

• V_o = 0 khi V₂ = V₁

• V_o > 0 khi V₂ > V₁

V_o = V_ss

• V_o < 0 khi V₂ < V₁

V_o = V_-ss

When two input voltages equal. The output voltage is zero . When the two input voltages different and if one is greater than or less than the other

1. V_o = V_ss khi V₂ > V₁
2. V_o = V_-ss khi V₂ < V₁

Instrumentation amplifier

Instrumentation amplifier

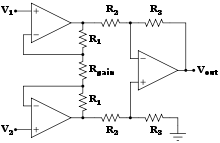
Combines very high input impedance, high common-mode rejection, low DC offset, and other properties used in making very accurate, low-noise measurements

• Is made by adding a inverting buffer to each input of the differential amplifier to increase the input impedance.

Schmitt trigger

Schmitt trigger

A comparator with hysteresis

Hysteresis from $\frac{-R_1}{R_2}V_{sat}$ to $\frac{R_1}{R_2}V_{sat}$.

Gyrator

Inductance gyrator

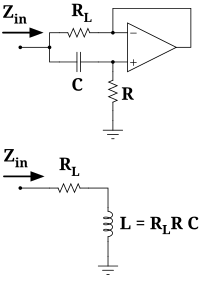
A gyrator can transform impedances. Here a capacitor is changed into an inductor.

$L = R_\mathrm{L} R C$

Zero level detector

Voltage divider reference

• Zener sets reference voltage

Negative impedance converter (NIC)

Negative impedance converter

Creates a resistor having a negative value for any signal generator

• In this case, the ratio between the input voltage and the input current (thus the input resistance) is given by:

$R_\mathrm{in} = - R_3 \frac{R_1}{R_2}$

Non-linear configurations

Rectifier

Super diode

Behaves like an ideal diode for the load, which is here represented by a generic resistor $R_\mathrm{L}$.

• This basic configuration has some limitations. For more information and to know the configuration that is actually used, see the main article.

Peak detector

Peak detector

When the switch is closed, the output goes to zero volts. When the switch is opened for a certain time interval, the capacitor will charge to the maximum input voltage attained during that time interval.

The charging time of the capacitor must be much shorter than the period of the highest appreciable frequency component of the input voltage.

Logarithmic output

Logarithmic configuration

• The relationship between the input voltage $v_\mathrm{in}$ and the output voltage $v_\mathrm{out}$ is given by:

$v_\mathrm{out} = -V_{\gamma} \ln \left( \frac{v_\mathrm{in}}{I_\mathrm{S} \cdot R} \right)$

where $I_\mathrm{S}$ is the saturation current.

• If the operational amplifier is considered ideal, the negative pin is virtually grounded, so the current flowing into the resistor from the source (and thus through the diode to the output, since the op-amp inputs draw no current) is:

$\frac{v_\mathrm{in}}{R} = I_\mathrm{R} = I_\mathrm{D}$

where $I_\mathrm{D}$ is the current through the diode. As known, the relationship between the current and the voltage for a diode is:

$I_\mathrm{D} = I_\mathrm{S} \left( e^{\frac{V_\mathrm{D}}{V_{\gamma}}} - 1 \right)$

This, when the voltage is greater than zero, can be approximated by:

$I_\mathrm{D} \simeq I_\mathrm{S} e^{V_\mathrm{D} \over V_{\gamma}}$

Putting these two formulae together and considering that the output voltage $V_\mathrm{out}$ is the inverse of the voltage across the diode $V_\mathrm{D}$, the relationship is proven.

Note that this implementation does not consider temperature stability and other non-ideal effects.

Exponential output

Exponential configuration

• The relationship between the input voltage $v_\mathrm{in}$ and the output voltage $v_\mathrm{out}$ is given by:

$v_\mathrm{out} = - R I_\mathrm{S} e^{v_\mathrm{in} \over V_{\gamma}}$

where $I_\mathrm{S}$ is the saturation current.

• Considering the operational amplifier ideal, then the negative pin is virtually grounded, so the current through the diode is given by:

$I_\mathrm{D} = I_\mathrm{S} \left( e^{\frac{V_\mathrm{D}}{V_{\gamma}}} - 1 \right)$

when the voltage is greater than zero, it can be approximated by:

$I_\mathrm{D} \simeq I_\mathrm{S} e^{V_\mathrm{D} \over V_{\gamma}}$

The output voltage is given by:

$v_\mathrm{out} = -R I_\mathrm{D}\,$