- Problem 1
Let  be the transformation that rotates
vectors clockwise by
be the transformation that rotates
vectors clockwise by  radians.
radians.
- Find the matrix
 representing
representing
 with respect to the standard bases.
Use Gauss' method to reduce
with respect to the standard bases.
Use Gauss' method to reduce  to the identity.
to the identity.
- Translate the row reduction to to a matrix equation
 (the prior item shows both that
(the prior item shows both that  is similar to
is similar to  , and that
no column operations are needed to derive
, and that
no column operations are needed to derive  from
from  ).
).
- Solve this matrix equation for
 .
.
- Sketch the geometric effect matrix, that is, sketch how
 is expressed as a
combination of dilations, flips, skews, and projections
(the identity is a trivial projection).
is expressed as a
combination of dilations, flips, skews, and projections
(the identity is a trivial projection).
- Answer
- To represent
 , recall that rotation counterclockwise by
, recall that rotation counterclockwise by
 radians is represented with respect to the standard basis
in this way.
radians is represented with respect to the standard basis
in this way.

A clockwise angle is the negative of a counterclockwise
one.

This Gauss-Jordan reduction
![{\displaystyle {\xrightarrow[{}]{\rho _{1}+\rho _{2}}}{\begin{pmatrix}{\sqrt {2}}/2&{\sqrt {2}}/2\\0&{\sqrt {2}}\end{pmatrix}}{\xrightarrow[{(1/{\sqrt {2}})\rho _{2}}]{(2/{\sqrt {2}})\rho _{1}}}{\begin{pmatrix}1&1\\0&1\end{pmatrix}}{\xrightarrow[{}]{-\rho _{2}+\rho _{1}}}{\begin{pmatrix}1&0\\0&1\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/faae28eb7d6e867ffd9a39f73f6bcf2b569fbd03)
produces the identity matrix
so there is no need for column-swapping operations
to end with a partial-identity.
- The reduction is expressed in matrix multiplication
as

(note that composition of the Gaussian operations is performed
from right to left).
- Taking inverses

gives the desired factorization of  (here, the partial
identity is
(here, the partial
identity is  , and
, and  is trivial, that is, it is also an identity
matrix).
is trivial, that is, it is also an identity
matrix).
- Reading the composition from right to left (and ignoring the
identity matrices as trivial) gives that
 has the same
effect as first performing this skew
has the same
effect as first performing this skew

followed by a dilation that multiplies all first components by
 (this is a "shrink" in that
(this is a "shrink" in that  )
and all second components by
)
and all second components by  ,
followed by another skew.
,
followed by another skew.
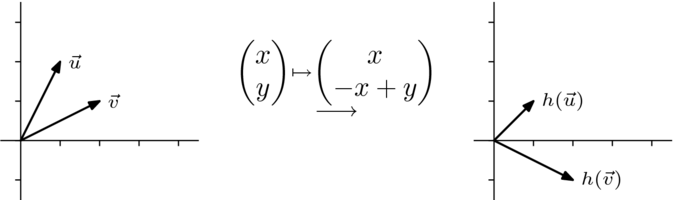
For instance, the effect of  on the unit vector whose angle with
the
on the unit vector whose angle with
the  -axis is
-axis is  is this.
is this.
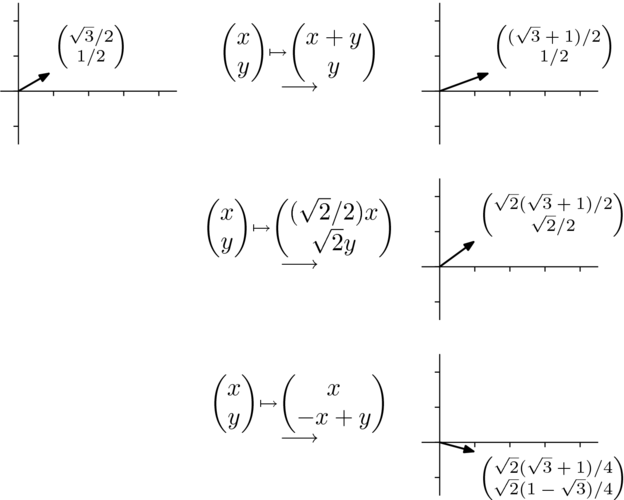
Verifying that the resulting vector has unit length and forms an
angle of  with the
with the  -axis is routine.
-axis is routine.
- Problem 2
What combination of dilations, flips, skews, and projections
produces a rotation counterclockwise by  radians?
radians?
- Answer
We will first represent the map with a matrix  ,
perform the row operations and, if needed, column operations
to reduce it to a partial-identity matrix.
We will then translate that into a factorization
,
perform the row operations and, if needed, column operations
to reduce it to a partial-identity matrix.
We will then translate that into a factorization  .
Subsitituting into the general matrix
.
Subsitituting into the general matrix

gives this representation.

Gauss' method is routine.
![{\displaystyle {\xrightarrow[{}]{{\sqrt {3}}\rho _{1}+\rho _{2}}}{\begin{pmatrix}-1/2&-{\sqrt {3}}/2\\0&-2\end{pmatrix}}{\xrightarrow[{(-1/2)\rho _{2}}]{-2\rho _{1}}}{\begin{pmatrix}1&{\sqrt {3}}\\0&1\end{pmatrix}}{\xrightarrow[{}]{-{\sqrt {3}}\rho _{2}+\rho _{1}}}{\begin{pmatrix}1&0\\0&1\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/443d4da6f31b7426c5d7799df1864905b916611c)
That translates to a matrix equation in this way.

Taking inverses to solve for  yields this factorization.
yields this factorization.

- Problem 3
What combination of dilations, flips, skews, and projections
produces the map  represented with respect to the standard bases by this matrix?
represented with respect to the standard bases by this matrix?

- Answer
This Gaussian reduction
![{\displaystyle {\xrightarrow[{-\rho _{1}+\rho _{3}}]{-3\rho _{1}+\rho _{2}}}{\begin{pmatrix}1&2&1\\0&0&-3\\0&0&1\end{pmatrix}}{\xrightarrow[{}]{(1/3)\rho _{2}+\rho _{3}}}{\begin{pmatrix}1&2&1\\0&0&-3\\0&0&0\end{pmatrix}}{\xrightarrow[{}]{(-1/3)\rho _{2}}}{\begin{pmatrix}1&2&1\\0&0&1\\0&0&0\end{pmatrix}}{\xrightarrow[{}]{-\rho _{2}+\rho _{1}}}{\begin{pmatrix}1&2&0\\0&0&1\\0&0&0\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0abe27d67c8beb79e1da4544e0b32614f3655bb8)
gives the reduced echelon form of the matrix.
Now the two column operations of taking  times the first column
and adding it to the second, and then of swapping columns two and three
produce this partial identity.
times the first column
and adding it to the second, and then of swapping columns two and three
produce this partial identity.

All of that translates into matrix terms as: where

and

the given matrix factors as  .
.
- Problem 5
Show that for any permutation
(that is, reordering)  of the numbers
of the numbers
 , ...,
, ...,  , the map
, the map

can be accomplished with a composition of maps,
each of which only swaps a single pair of coordinates.
Hint: it can be done by induction on  .
(Remark: in the fourth chapter we will show this and we will also
show that the parity of the number of swaps used is determined by
.
(Remark: in the fourth chapter we will show this and we will also
show that the parity of the number of swaps used is determined by  .
That is, although a particular
permutation could be accomplished in two different ways
with two different numbers of swaps, either both ways use an even number of
swaps, or both use an odd number.)
.
That is, although a particular
permutation could be accomplished in two different ways
with two different numbers of swaps, either both ways use an even number of
swaps, or both use an odd number.)
- Answer
We can show this by induction on the number of components in the
vector.
In the  base case the only permutation is the trivial one,
and the map
base case the only permutation is the trivial one,
and the map

is indeed expressible as a composition of swaps— as zero swaps.
For the inductive step we assume that the map induced by
any permutation of fewer than
 numbers can be expressed with swaps only, and we consider the map
induced by a
permutation
numbers can be expressed with swaps only, and we consider the map
induced by a
permutation  of
of  numbers.
numbers.

Consider the number  such that
such that  .
The map
.
The map

will, when followed by the swap of the  -th and
-th and  -th components, give the map
-th components, give the map  . Now, the inductive hypothesis gives that
. Now, the inductive hypothesis gives that  is achievable as a composition of swaps.
is achievable as a composition of swaps.
- Problem 6
Show that linear maps preserve the linear structures of a space.
- Show that for any linear map from
 to
to  ,
the image of any line is a line.
The image may be a degenerate line, that is, a single point.
,
the image of any line is a line.
The image may be a degenerate line, that is, a single point.
- Show that the image of any linear surface is a linear surface.
This generalizes the result that under a linear map the image of
a subspace is a subspace.
- Linear maps preserve other linear ideas.
Show that linear maps preserve "betweeness": if the point
 is between
is between  and
and  then the image of
then the image of  is between the
image of
is between the
image of  and the image of
and the image of  .
.
- Answer
- A line is a subset of
 of the form
of the form
 .
The image of a point on that line is
.
The image of a point on that line is
 ,
and the set of such vectors, as
,
and the set of such vectors, as  ranges over the reals, is
a line (albeit, degenerate if
ranges over the reals, is
a line (albeit, degenerate if  ).
).
- This is an obvious extension of the prior argument.
- If the point
 is between the points
is between the points  and
and  then the
line from
then the
line from  to
to  has
has  in it.
That is, there is a
in it.
That is, there is a  such that
such that
 (where
(where  is the
endpoint of
is the
endpoint of  , etc.).
Now, as in the argument of the first item, linearity shows that
, etc.).
Now, as in the argument of the first item, linearity shows that
 .
.









![{\displaystyle {\xrightarrow[{}]{\rho _{1}+\rho _{2}}}{\begin{pmatrix}{\sqrt {2}}/2&{\sqrt {2}}/2\\0&{\sqrt {2}}\end{pmatrix}}{\xrightarrow[{(1/{\sqrt {2}})\rho _{2}}]{(2/{\sqrt {2}})\rho _{1}}}{\begin{pmatrix}1&1\\0&1\end{pmatrix}}{\xrightarrow[{}]{-\rho _{2}+\rho _{1}}}{\begin{pmatrix}1&0\\0&1\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/faae28eb7d6e867ffd9a39f73f6bcf2b569fbd03)







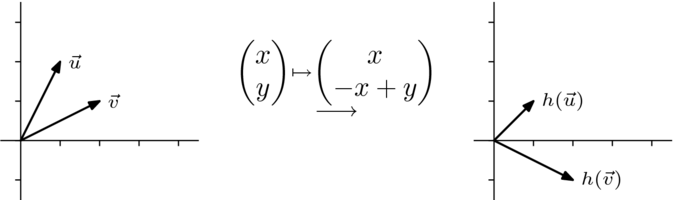


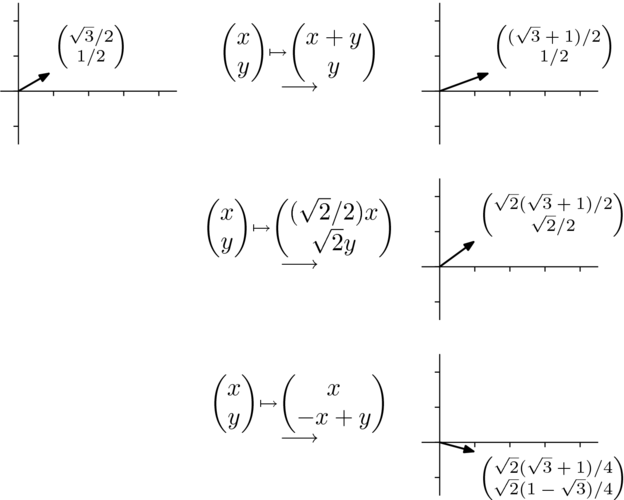





![{\displaystyle {\xrightarrow[{}]{{\sqrt {3}}\rho _{1}+\rho _{2}}}{\begin{pmatrix}-1/2&-{\sqrt {3}}/2\\0&-2\end{pmatrix}}{\xrightarrow[{(-1/2)\rho _{2}}]{-2\rho _{1}}}{\begin{pmatrix}1&{\sqrt {3}}\\0&1\end{pmatrix}}{\xrightarrow[{}]{-{\sqrt {3}}\rho _{2}+\rho _{1}}}{\begin{pmatrix}1&0\\0&1\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/443d4da6f31b7426c5d7799df1864905b916611c)




![{\displaystyle {\xrightarrow[{-\rho _{1}+\rho _{3}}]{-3\rho _{1}+\rho _{2}}}{\begin{pmatrix}1&2&1\\0&0&-3\\0&0&1\end{pmatrix}}{\xrightarrow[{}]{(1/3)\rho _{2}+\rho _{3}}}{\begin{pmatrix}1&2&1\\0&0&-3\\0&0&0\end{pmatrix}}{\xrightarrow[{}]{(-1/3)\rho _{2}}}{\begin{pmatrix}1&2&1\\0&0&1\\0&0&0\end{pmatrix}}{\xrightarrow[{}]{-\rho _{2}+\rho _{1}}}{\begin{pmatrix}1&2&0\\0&0&1\\0&0&0\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0abe27d67c8beb79e1da4544e0b32614f3655bb8)






































