Introduction to Inorganic Chemistry/Coordination Chemistry and Crystal Field Theory
Chapter 5: Coordination Chemistry and Crystal Field Theory[edit | edit source]

Coordination compounds (or complexes) are molecules and extended solids that contain bonds between a transition metal ion and one or more ligands. In forming these coordinate covalent bonds, the metal ions act as Lewis acids and the ligands act as Lewis bases. Typically, the ligand has a lone pair of electrons, and the bond is formed by overlap of the molecular orbital containing this electron pair with the d-orbitals of the metal ion. Ligands that are commonly found in coordination complexes are neutral molecules (H2O, NH3, organic bases such as pyridine, CO, NO, H2, ethylene, and phosphines PR3) and anions (halides, CN-, SCN-, cyclopentadienide (C5H5-), H-, etc.). The resulting complexes can be cationic (e.g., [Cu(NH3)4]2+), neutral ([Pt(NH3)2Cl2]) or anionic ([Fe(CN)6]4-). As we will see below, ligands that have weak or negligible strength as Brønsted bases (for example, CO, CN-, H2O, and Cl-) can still be potent Lewis bases in forming transition metal complexes.
With ligands that are Lewis bases, coordinate covalent bonds (also called dative bonds) are typically drawn as lines, or sometimes as arrows to indicate that the electron pair "belongs" to the ligand X:

In counting electrons on the metal (described below), the convention is to assign both electrons in the dative bond to the ligand, although in reality the bonds are typically polar covalent and electrons are shared between the metal and the ligand.
When writing out the formulas of coordination compounds, we use square brackets [...] around the metal ions and ligands that are directly bonded to each other. Thus the compound [Co(NH3)5Cl]Cl2 contains octahedral [Co(NH3)5Cl]2+ ions, in which five ammonia molecules and one chloride ion are directly bonded to the metal, and two Cl- anions that are not coordinated to the metal.



History. Coordination compounds have been known for centuries, but their structures were initially not understood. For example, Prussian Blue, which has an empirical formula Fe7(CN)18•xH2O, is an insoluble, deep blue solid that has been used as a pigment since its accidental discovery by Diesbach in 1704. Prussian Blue actually contains Fe3+ cations and [Fe(CN)6]4- anions, and a more descriptive formulation is (Fe3+)4([Fe(CN)6]4-)3•xH2O. Simpler compounds such as the ammonia complex of Co3+ were known to chemists but did not fit the expected behavior of ionic solids. For example, cobalt(III)hexammine chloride, [Co(NH3)6]Cl3 was formulated as CoCl3•6NH3. It had mysterious properties, in that it dissolved in water like an ionic solid, but it retained its six ammonia molecules when recrystallized. Even more intriguing was the observation that chemically different forms (isomers) of transition metal complexes such as [Co(NH3)4Cl2]Cl could be made. The puzzle was solved by Alfred Werner, who proposed in 1893 that these Co complexes contained octahedrally coordinated metal ions that made primary (covalent) bonds to six ligands. Werner showed through conductivity measurements that solutions of CoCl3•6NH3 contained three free Cl- anions and one [Co(NH3)6]3+ cation per formula unit. Magnetic susceptibility measurements later confirmed the presence of diamagnetic Co3+ in both the salt and its solutions. Werner's theory also explained the existence of two (and only two) structural isomers for [Co(NH3)4Cl2]+.
Like organic compounds, transition metal complexes can vary widely in size, shape, charge and stability. We will see that bonds formed from the d-orbitals of the metal largely control these properties.
Learning goals for Chapter 5:
- Determine oxidation states and assign d-electron counts for transition metals in complexes.
- Derive the d-orbital splitting patterns for octahedral, elongated octahedral, square pyramidal, square planar, and tetrahedral complexes.
- For octahedral and tetrahedral complexes, determine the number of unpaired electrons and calculate the crystal field stabilization energy.
- Know the spectrochemical series, rationalize why different classes of ligands impact the crystal field splitting energy as they do, and use it to predict high vs. low spin complexes, and the colors of transition metal complexes.
- Use the magnetic moment of transition metal complexes to determine their spin state.
- Understand the origin of the Jahn-Teller effect and its consequences for complex shape, color, and reactivity.
- Understand the extra stability of complexes formed by chelating and macrocyclic ligands.
5.1 Counting electrons in transition metal complexes[edit | edit source]
The d-orbitals are the frontier orbitals (the HOMO and LUMO) of transition metal complexes. Many of the important properties of complexes - their shape, color, magnetism, and reactivity - depend on the electron occupancy of the metal's d-orbitals. To understand and rationalize these properties it is important to know how to count the d-electrons.
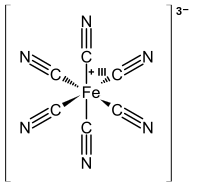
Because transition metals are generally less electronegative than the atoms on the ligands (C, N, O, Cl, P...) that form the metal-ligand bond, our convention is to assign both electrons in the bond to the ligand. For example, in the ferricyanide complex [Fe(CN)6]3-, if the cyanide ligand keeps both of its electrons it is formulated as CN-. By difference, iron must be Fe3+ because the charges (3+ + 6(1-)) must add up to the overall -3 charge on the complex.
The next step is to determine how many d-electrons the Fe3+ ion has. The rule is to count all of iron's valence electrons as d-electrons. Iron is in group 8, so
- group 8 - 3+ charge = d5 (or 3d5)
- 8 - 3 = 5
The same procedure can be applied to any transition metal complex. For example, consider the complex [Cu(NH3)4]2+. Because ammonia is a neutral ligand, Cu is in the 2+ oxidation state. Copper (II), in group 11 of the periodic table has 11 electrons in its valence shell, minus two, leaving it with 9 d-electrons (3d9). In the neutral complex [Rh(OH)3(H2O)3], Rh is in the +3 oxidation state and is in group 9, so the electron count is 4d6. Zinc(II) in group 12 would have 10 d-electrons in [Zn(NH3)4]2+, a full shell, and manganese (VII) has zero d-electrons in MnO4-. Nickel carbonyl, Ni(CO)4, contains the neutral CO ligand and Ni in the zero oxidation state. Since Ni is in group 10, we count the electrons on Ni as 3d10.
A frequent source of confusion about electron counting is the fate of the s-electrons on the metal. For example, our electron counting rules predict that Ti is 3d1 in the octahedral complex [Ti(H2O)6]3+. But the electronic configuration of a free Ti atom, according to the Aufbau principle, is 4s23d2. Why is the Ti3+ ion 3d1 and not 4s1? Similarly, why do we assign Mn2+ as 3d5 rather than 4s23d3? The short answer is that the metal s orbitals are higher in energy in a metal complex than they are in the free atom because they have antibonding character. We will justify this statement with a MO diagram in Section 5.2.
Covalent Bond Classification (CBC) Method. Although the electron counting rule we have developed above is useful and works reliably for all kinds of complexes, the assignment of all the shared electrons in the complex to the ligands does not always represent the true bonding picture. This picture would be most accurate in the case of ligands that are much more electronegative than the metal. But in fact, there all all kinds of ligands, including those such as H, alkyl, cyclopentadienide, and others where the metal and ligand have comparable electronegativity. In those cases, especially with late transition metals that are relatively electronegative, we should regard the metal-ligand bond as covalent. The CBC method, also referred to as LXZ notation, was introduced in 1995 by M. L. H. Green[2] in order to better describe the different kinds of metal-ligand bonds. The molecular orbital pictures below summarize the difference between L, X, and Z ligands.[3] Of these, L and X are the most common types.

L-type ligands are Lewis bases that donate two electrons to the metal center regardless of the electron counting method being used. These electrons can come from lone pairs, pi or sigma donors. The bonds formed between these ligands and the metal are dative covalent bonds, which are also known as coordinate bonds. Examples of this type of ligand include CO, PR3, NH3, H2O, carbenes (=CRR'), and alkenes.


X-type ligands are those that donate one electron to the metal and accept one electron from the metal when using the neutral ligand method of electron counting, or donate two electrons to the metal when using the donor pair method of electron counting.[4] Regardless of whether it is considered neutral or anionic, these ligands yield normal covalent bonds. A few examples of this type of ligand are H, CH3, halogens, and NO (bent).
Z-type ligands are those that accept two electrons from the metal center as opposed to the donation occurring with the other two types of ligands. However, these ligands also form dative covalent bonds like the L-type. This type of ligand is not usually used, because in certain situations it can be written in terms of L and X. For example, if a Z ligand is accompanied by an L type, it can be written as X2. Examples of these ligands are Lewis acids, such as BR3.
Some multidentate ligands can act as a combination of ligand types. A famous example is the cyclopentadienyl (or Cp) ligand, C5H5. We would classify this neutral ligand as [L2X], with the two L functionalities corresponding to the two “olefinic” fragments while the X functionality corresponds to the CH “radical” carbon in the ring. The addition of one electron makes the Cp- anion, which has six pi electrons and is thus planar and aromatic. In the ferrocene complex, Cp2Fe, using the "standard" donor pair counting method we can regard the two Cp- ligands as each possessing six pi electrons, and by difference Fe is in the +2 oxidation state. The Fe2+ ion is d6. Thus the iron atom in the complex (regardless of the counting method) has 6+6+6=18 electrons in its coordination environment, which is a particularly stable electron count for transition metal complexes.
5.2 Crystal field theory[edit | edit source]
Crystal field theory is one of the simplest models for explaining the structures and properties of transition metal complexes. The theory is based on the electrostatics of the metal-ligand interaction, and so its results are only approximate in cases where the metal-ligand bond is substantially covalent. But because the model makes effective use of molecular symmetry, it can be surprisingly accurate in describing the magnetism, colors, structure, and relative stability of metal complexes.
Consider a positvely charged metal ion such as Fe3+ in the "field" of six negatively charged ligands, such as CN-. There are two energetic terms we need to consider. The first is the electrostatic attraction between the metal and ligands, which is inversely proportional to the distance between them:
The second term is the repulsion that arises from the Pauli exclusion principle when a third electron is added to a filled orbital. There is no place for this third electron to go except to a higher energy antibonding orbital. This is the situation when a ligand lone pair approaches an occupied metal d-orbital:

Now let us consider the effect of these attractive and repulsive terms as the metal ion and ligands are brought together. We do this in two steps, first forming a ligand "sphere" around the metal and then moving the six ligands to the vertices of an octahedron. Initially all five d-orbitals are degenerate, i.e., they have the same energy by symmetry. In the first step, the antibonding interaction drives up the energy of the orbitals, but they remain degenerate. In the second step, the d-orbitals split into two symmetry classes, a lower energy, triply-degenerate set (the t2g orbitals) and a higher energy, doubly degenerate set (the eg orbitals).
The energy difference between the eg and t2g orbitals is given the symbol ΔO, where the "O" stands for "octahedral." We will see that this splitting energy is sensitive to the degree of orbital overlap and thus depends on both the metal and the ligand. Relative to the midpoint energy (the barycenter), the t2g orbitals are stabilized by 2/5 ΔO and the eg orbitals are destabilized by 3/5 ΔO in an octahedral complex.

What causes the d-orbitals to split into two sets? Recall that the d-orbitals have a specific orientation with respect to the Cartesian axes. The lobes of the dxy, dxz, and dyz orbitals (the t2g orbitals) lie in the xy-, xz-, and yz-planes, respectively. These three d-orbitals have nodes along the x-, y-, and z-directions. The orbitals that contain the ligand lone pairs are oriented along these axes and therefore have zero overlap with the metal t2g orbitals. It is easy to see that these three d-orbitals must be degenerate by symmetry. On the other hand, the lobes of the dz2 and dx2-y2 orbitals (the eg orbitals) point directly along the bonding axes and have strong overlap with the ligand orbitals. While it is less intuitively obvious, these orbitals are also degenerate by symmetry and have antibonding character.
It is informative to compare the results of crystal field theory and molecular orbital theory (also called ligand field theory in this context) for an octahedral transition metal complex. The energy level diagrams below make this comparison for the d1 octahedral ion [Ti(H2O)6]3+. In the MO picture at the right, the frontier orbitals are derived from the metal d-orbitals. The lower t2g set, which contains one electron, is non-bonding by symmetry, and the eg orbitals are antibonding. The metal 4s orbital, which has a1g symmetry, makes a low energy bonding combination that is ligand-centered, and an antibonding combination that is metal-centered and above the eg levels. This is the reason that our d-electron counting rules do not need to consider the metal 4s orbital. The important take-home message is that crystal field theory and MO theory give very similar results for the frontier orbitals of transition metal complexes.
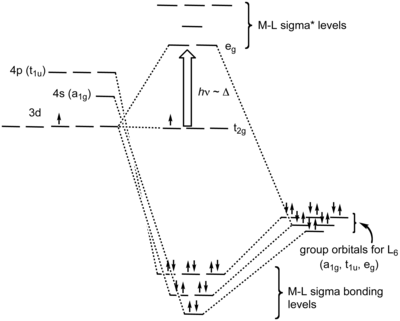

5.3 Spectrochemical series[edit | edit source]

Strong and weak field ligands. The spectrochemical series ranks ligands according the energy difference ΔO between the t2g and eg orbitals in their octahedral complexes. This energy difference is measured in the spectral transition between these levels, which often lies in the visible part of the spectrum and is responsible for the colors of complexes with partially filled d-orbitals. Ligands that produce a large splitting are called strong field ligands, and those that produce a small splitting are called weak field ligands.
An abbreviated spectrochemical series is:
Weak field I- < Br- < Cl- < NO3- < F- < OH- < H2O < Pyridine < NH3 < NO2- < CN- < CO Strong field


Orbital overlap. Referring to the molecular orbital diagram above, we see that the splitting between d-electron levels reflects the antibonding interaction between the eg metal orbitals and the ligands. Thus, we expect ligand field strength to correlate with metal-ligand orbital overlap. Ligands that bind through very electronegative atoms such as O and halogens are thus expected to be weak field, and ligands that bind through C or P are typically strong field. Ligands that bind through N are intermediate in strength. Another way to put this is that hard bases tend to be weak field ligands and soft bases are strong field ligands.
- Energy units. Energy can be calculated in a number of ways and it is useful to try to relate the splitting energy ΔO to more familiar quantities like bond energies.
- When ΔO is measured optically, a photon of wavelength λ is absorbed as an electron is promoted from a t2g to an eg orbital. The photon energy is related to its wavelength and frequency by:
- E = hν = hc/λ = hc
- Here ν is the frequency of the electromagnetic radiation, h is Planck's constant (6.626x10-34 J*s), and c is the speed of light. is called the "wavenumber" and is the inverse of the wavelength, usually measured in cm-1. Energy gaps are often expressed by spectroscopists in terms of wavenumbers.
- For example, a red photon has a wavelength of about 620 nm and a wavenumber of about 16,000 cm-1. In other energy units, the same red photon has an energy of 2.0 eV (1 eV = 1240 nm) or 193 kJ/mol (1 eV = 96.5 kJ/mol). If we compare this to the dissociation energy of a carbon-carbon single bond (350 kJ/mol), we see that the C-C bond has about twice the energy of a red photon. We would need an ultraviolet photon (E > 350 kJ/mol = 3.6 eV = 345 nm = 29,000cm-1) to break a C-C bond.
We will see that ΔO varies widely for transition metal complexes, from near-infrared to ultraviolet wavelengths. Thus the energy difference between the t2g and eg orbitals can range between the energy of a rather weak to a rather strong covalent bond.
ΔO depends on both the metal and the ligand. We can learn something about trends in ΔO by comparing a series of d6 metal complexes:
Complex ΔO (cm-1) [Co(H2O)6]2+ 9,300 [Co(H2O)6]3+ 18,200 [Co(CN)6]3- 33,500 [Rh(H2O)6]3+ 27,000 [Rh(CN)6]3- 45,500
Important trends in ΔO:
- Co3+ complexes have larger ΔO than Co2+ complexes with the same ligand. This reflects the electrostatic nature of the crystal field splitting.
- Rh3+ complexes have larger ΔO than Co3+ complexes. In general, elements in the 2nd and 3rd transition series (the 4d and 5d elements) have larger splitting than those in the 3d series.
- For a given metal in one oxidation state (e.g., Co3+), the trend in ΔO follows the spectrochemical series. Thus ΔO is larger for [Co(CN)6]3-, which contains the strong field CN- ligand, than it is for [Co(H2O)6]3+ with the weak field ligand H2O.

The 4d and 5d elements are similar in their size and their chemistry. In comparing ΔO values for complexes in the 3d, 4d, and 5d series (e.g., comparing elements in the triads Co,Rh,Ir or Fe,Ru,Os), we always find 3d << 4d ≲ 5d. This trend reflects the spatial extent of the d-orbitals and thus their overlap with ligand orbitals. The 3d orbitals are smaller, and they are less effective in bonding than the 4d or 5d. The 4d and 5d orbitals are similar to each other because of the lanthanide contraction. At the beginning of the 5d series (between 56Ba and 72Hf) are the fourteen lanthanide elements (57La - 71Lu).
Although the valence orbitals of the 5d elements are in a higher principal quantum shell than those of the 4d elements, the addition of 14 protons to the nucleus in crossing the lanthanide series contracts the sizes of the atomic orbitals. The important result is that the valence orbitals of the 4d and 5d elements have similar sizes and thus the elements resemble each other in their chemistry much more than they resemble their cousins in the 3d series. For example, the chemistry of Ru is very similar to that of Os, as illustrated at the right, but quite different from that of Fe.
Colors of transition metal complexes. A simple, qualitative way to see the relative crystal field splitting energy, ΔO, is to observe the color of a transition metal complex. The higher the energy of the absorbed photon, the larger the energy gap. However, the color a complex absorbs is complementary to the color it appears (i.e., the color of light it reflects), which is opposite the absorbed color on the color wheel.
Examples: (all d7 Co2+ complexes)
[Co(H2O)6]2+ looks purple in its salts and in concentrated solution because it absorbs in the green range.
[Co(NH3)6]2+ is straw-colored because it absorbs in the blue range.
[Co(CN)6]4-, looks red, absorbs in the violet and ultra-violet part of the spectrum. This is consistent with the idea that CN- is a stronger field ligand than NH3, because the energy of a UV photon is higher than that of a red-orange photon.
This method is applicable to most transition metal complexes, as the majority of them absorb somewhere in the visible range (400-700 nm = 25,000 to 14,300 cm-1), or have UV transitions that tail into the visible, making them appear yellow; however there are complexes such as [Rh(CN)6]3- that appear colorless because their d-d transitions are in the ultraviolet. Other complexes such as [Mn(H2O)]62+ are weakly colored because their d-d transitions involve a change in the spin state of the complex.
5.4 π-bonding between metals and ligands[edit | edit source]

An important factor that contributes to the high ligand field strength of ligands such as CO, CN-, and phosphines is π-bonding between the metal and the ligand. There are three types of pi-bonding in metal complexes:

The most common situation is when a ligand such as carbon monoxide or cyanide donates its sigma (nonbonding) electrons to the metal, while accepting electron density from the metal through overlap of a metal t2g orbital and a ligand π* orbital. This situation is called "back-bonding" because the ligand donates σ-electron density to the metal and the metal donates π-electron density to the ligand. The ligand is thus acting as a σ-donor and a π-acceptor. In π-backbonding, the metal donates π electrons to the ligand π* orbital, adding electron density to an antibonding molecular orbital. This results in weakening of the C-O bond, which is experimentally observed as lengthening of the bond (relative to free CO in the gas phase) and lowering of the C-O infrared stretching frequency.
d-d π bonding occurs when an element such phosphorus, which has a σ-symmetry lone pair and an empty 3d orbital, binds to a metal that has electrons in a t2g orbital. This is a common situation for phosphine complexes (e.g., triphenylphosphine) bound to low-valent, late transition metals. The backbonding in this case is analogous to the CO example, except that the acceptor orbital is a phosphorus 3d orbital rather than a ligand π* orbital. Here the phosphine ligand acts as a σ-donor and a π-acceptor, forming a dπ-dπ bond.
The third kind of metal-ligand π-bonding occurs when a π-donor ligand - an element with both a σ-symmetry electron pair and a filled orthogonal p-orbital - bonds to a metal, as shown above at the right for an O2- ligand. This occurs in early transition metal complexes. In this example, O2- is acting as both a σ-donor and a π-donor. This interaction is typically drawn as a metal-ligand multiple bond, e.g., the V=O bond in the vanadyl cation [VO]2+. Typical π-donor ligands are oxide (O2-), nitride (N3-), imide (RN2-), alkoxide (RO-), amide (R2N-), and fluoride (F-). For late transition metals, strong π-donors form anti-bonding interactions with the filled d-levels, with consequences for spin state, redox potentials, and ligand exchange rates. π-donor ligands are low in the spectrochemical series.[5]


Carbon-containing ligands that are π-donors and their complexes with transition metal ions are very important in olefin metathesis, a reaction in which carbon-carbon double bonds are interchanged. Using these catalysts, cyclic olefins can be transformed into linear polymers in high yield through ring-opening metathesis polymerization (ROMP). Catalysts of this kind were developed by the groups of Richard Schrock and Robert Grubbs, who shared the 2005 Nobel Prize in Chemistry with Yves Chauvin for their discoveries. The Schrock catalysts are based on early transition metals such as Mo; they are more reactive but less tolerant of different organic functional groups and protic solvents than the Grubbs catalysts, which are based on Ru complexes.
5.5 Crystal field stabilization energy, pairing, and Hund's rule[edit | edit source]
The splitting of the d-orbitals into different energy levels in transition metal complexes has important consequences for their stability, reactivity, and magnetic properties. Let us first consider the simple case of the octahedral complexes [M(H2O)6]3+, where M = Ti, V, Cr. Because the complexes are octahedral, they all have the same energy level diagram:

The Ti3+, V3+, and Cr3+ complexes have one, two and three d-electrons respectively, which fill the degenerate t2g orbitals singly. The spins align parallel according to Hund's rule, which states that the lowest energy state has the highest spin angular momentum.
For each of these complexes we can calculate a crystal field stabilization energy, CFSE, which is the energy difference between the complex in its ground state and in a hypothetical state in which all five d-orbitals are at the energy barycenter.
- For Ti3+, there is one electron stabilized by 2/5 ΔO, so CFSE = -(1)(2/5)(ΔO) = -2/5 ΔO.
- Similarly, CFSE = -4/5 ΔO and -6/5 ΔO for V3+ and Cr3+, respectively.
For Cr2+ complexes, which have four d-electrons, the situation is more complicated. Now we can have a high spin configuration (t2g)3(eg)1, or a low spin configuration (t2g)4(eg)0 in which two of the electrons are paired. What are the energies of these two states?
- High spin: CFSE = (-3)(2/5)ΔO + (1)(3/5)ΔO = -3/5 ΔO
- Low spin: CFSE = (-4)(2/5)ΔO + P = -8/5 ΔO + P, where P is the pairing energy
- Energy difference = -8/5 ΔO + P - (-3/5 ΔO) = -ΔO + P
The pairing energy P is the energy penalty for putting two electrons in the same orbital, resulting from the electrostatic repulsion between electrons. For 3d elements, a typical value of P is about 15,000 cm-1.
The important result here is that a complex will be low spin if ΔO > P, and high spin if ΔO < P.
Because ΔO depends on both the metals and the ligands, it determines the spin state of the complex.

Rules of thumb:
- 3d complexes are high spin with weak field ligands and low spin with strong field ligands.
- High valent 3d complexes (e.g., Co3+ complexes) tend to be low spin (large ΔO)
- 4d and 5d complexes are always low spin (large ΔO)
Note that high and low spin states occur only for 3d metal complexes with between 4 and 7 d-electrons. Complexes with 1 to 3 d-electrons can accommodate all electrons in individual orbitals in the t2g set. Complexes with 8, 9, or 10 d-electrons will always have completely filled t2g orbitals and 2-4 electrons in the eg set.
Examples of high and low spin complexes:
- [Co(H2O)62+] contains a d7 metal ion with a weak field ligand. This complex is known to be high spin from magnetic susceptibility measurements, which detect three unpaired electrons per molecule. Its orbital occupancy is (t2g)5(eg)2.
- We can calculate the CFSE as -(5)(2/5)ΔO + (2)(3/5)ΔO = -4/5 ΔO.
- [Co(CN)64-] is also an octahedral d7 complex but it contains CN-, a strong field ligand. Its orbital occupancy is (t2g)6(eg)1 and it therefore has one unpaired electron.
- In this case the CFSE is -(6)(2/5)ΔO + (1)(3/5)ΔO + P = -9/5 ΔO + P.
Magnetism of transition metal complexes
Compounds with unpaired electrons have an inherent magnetic moment that arises from the electron spin. Such compounds interact strongly with applied magnetic fields. Their magnetic susceptibility provides a simple way to measure the number of unpaired electrons in a transition metal complex.
If a transition metal complex has no unpaired electrons, it is diamagnetic and is weakly repelled from the high field region of an inhomogeneous magnetic field. Complexes with unpaired electrons are typically paramagnetic. The spins in paramagnets align independently in an applied magnetic field but do not align spontaneously in the absence of a field. Such compounds are attracted to a magnet, i.e., they are drawn into the high field region of an inhomogeneous field. The attractive force, which can be measured with a Guoy balance or a SQUID magnetometer, is proportional to the magnetic susceptibility (χ) of the complex.
The effective magnetic moment of an ion (µeff), in the absence of spin-orbit coupling, is given by the sum of its spin and orbital moments:
- µeff = µspin + µorbital = µs + µL
In octahedral 3d metal complexes, the orbital angular momentum is largely "quenched" by symmetry, so we can approximate:
- µeff ≈ µs
We can calculate µs from the number of unpaired electrons (n) using:
Here µB is the Bohr magneton (= eh/4πme) = 9.3 x 10-24 J/T. This spin-only formula is a good approximation for first-row transition metal complexes, especially high spin complexes. The table below compares calculated and experimentally measured values of µeff for octahedral complexes with 1-5 unpaired electrons.
Ion Number of
unpaired
electronsSpin-only
moment /μBobserved
moment /μBTi3+ 1 1.73 1.73 V4+ 1 1.68–1.78 Cu2+ 1 1.70–2.20 V3+ 2 2.83 2.75–2.85 Ni2+ 2 2.8–3.5 V2+ 3 3.87 3.80–3.90 Cr3+ 3 3.70–3.90 Co2+ 3 4.3–5.0 Mn4+ 3 3.80–4.0 Cr2+ 4 4.90 4.75–4.90 Fe2+ 4 5.1–5.7 Mn2+ 5 5.92 5.65–6.10 Fe3+ 5 5.7–6.0
The small deviations from the spin-only formula for these octahedral complexes can result from the neglect of orbital angular momentum or of spin-orbit coupling. Tetrahedral d3, d4, d8 and d9 complexes tend to show larger deviations from the spin-only formula than octahedral complexes of the same ion because quenching of the orbital contribution is less effective in the tetrahedral case.
Summary of rules for high and low spin complexes:

- 3d complexes: Can be high or low spin, depending on the ligand (d4, d5, d6, d7)
- 4d and 5d complexes: Always low spin, because ΔO is large
- Maximum CFSE is for d3 and d8 cases (e.g., Cr3+, Ni2+) with weak field ligands (H2O, O2-, F-,...) and for d3-d6 with strong field ligands (Fe2+, Ru2+, Os2+, Co3+, Rh3+, Ir3+,...)
- Irving-Williams series. For M2+ complexes, the stability of the complex follows the order Mg2+ < Mn2+ < Fe2+ < Co2+ < Ni2+ < Cu2+ > Zn2+. This trend represents increasing Lewis acidity as the ions become smaller (going left to right in the periodic table) as well as the trend in CFSE. This same trend is reflected in the hydration enthalpy of gas-phase M2+ ions, as illustrated in the graph at the right. Note that Ca2+, Mn2+, and Zn2+, which are d0, d5(high spin), and d10 aquo ions, respectively, all have zero CFSE and fall on the same line. Ions that deviate the most from the line such as Ni2+ (octahedral d8) have the highest CFSE.

Colors and spectra of transition metal complexes
Transition metal complexes often have beautiful colors because, as noted above, their d-d transition energies can be in the visible part of the spectrum. With octahedral complexes these colors are faint (the transitions are weak) because they violate the Laporte selection rule. According to this rule, g -> g and u -> u transitions are forbidden in centrosymmetric complexes. d-orbitals have g (gerade) symmetry, so d-d transitions are Laporte-forbidden. However octahedral complexes can absorb light when they momentarily distort away from centrosymmetry as the molecule vibrates. Spin flips are also forbidden in optical transitions by the spin selection rule, so the excited state will always have the same spin multiplicity as the ground state.
The spectra of even the simplest transition metal complexes are rather complicated because of the many possible ways in which the d-electrons can fill the t2g and eg orbitals. For example, if we consider a d2 complex such as V3+(aq), we know that the two electrons can reside in any of the five d-orbitals, and can either be spin-up or spin-down. There are actually 45 different such arrangements (called microstates) that do not violate the Pauli exclusion principle for a d2 complex. Usually we are concerned only with the six of lowest energy, in which both electrons occupy individual orbitals in the t2g set and all their spins are aligned either up or down.

We can see how these microstates play a role in electronic spectra when we consider the d-d transitions of the [Cr(NH3)6]3+ ion. This ion is d3, so each of the three t2g orbitals contains one unpaired electron. We expect to see a transition when one of the three electrons in the t2g orbitals is excited to an empty eg orbital. Interestingly, we find not one but two transitions in the visible.
The reason that we see two transitions is that the electron can come from any one of the t2g orbitals and end up in either of the eg orbitals. Let us assume for the sake of argument that the electron is initially in the dxy orbital. It can be excited to either the dz2 or the dx2-y2 orbital:
- dxy --> dz2 (higher energy)
- dxy --> dx2-y2 (lower energy)
The first transition is at higher energy (shorter wavelength) because in the excited state the configuration is (dyz1dxz1dz21). All three of the excited state orbitals have some z-component, so the d-electron density is "piled up" along the z-axis. The energy of this transition is thus increased by electron-electron repulsion. In the second case, the excited state configuration is (dyz1dxz1dx2-y21), and the d-electrons are more symmetrically distributed around the metal. This effect is responsible for a splitting of the d-d bands by about 8,000 cm-1. We can show that all other possible transitions are equivalent to one of these two by symmetry, and hence we see only two visible absorption bands for Cr3+ complexes.
5.6 Non-octahedral complexes[edit | edit source]


The most important non-octahedral geometries for transition metal complexes are:
- 4-coordinate: square planar and tetrahedral
- 5-coordinate: square pyramidal and trigonal bipyramidal


Energies of the d-orbitals in non-octahedral geometries. The figure at the left shows what happens to the d-orbital energy diagram as we progressively distort an octahedral complex by elongating it along the z-axis (a tetragonal distortion), by removing one of its ligands to make a square pyramid, or by removing both of the ligands along the z-axis to make a square planar complex. In all cases, we keep the total bond order the same by making the bonds in the xy plane shorter as the bonds in the z-direction are stretched and/or broken.
The distortion away from octahedral symmetry breaks the degeneracy of the t2g and eg orbitals. d-orbitals with a z-component (dxz, dyz, dz2) go down in energy as orbitals that reside in the xy plane (dxy, dx2-y2) rise in energy. The barycenter (the weighted average orbital energy) remains constant. Also, it is important to note that the splitting between the dxy and dx2-y2 orbitals stays constant at ΔO regardless of the nature of the distortion.
Why would a "happy" octahedral complex want to lose two of its ligands to make a square planar complex? This occurs frequently in d8 and sometimes in d9 complexes with large ΔO, i.e., 3d8 complexes with strong field ligands and 4d8, 5d8 complexes with any ligands. Examples of such d8 complexes are [Ni(CN)4]2-, the anti-cancer drug cisplatin (cis-Pt(NH3)2Cl2), [Pd(H2O)4]2+, and [AuCl4]-. At the d8 electron count, the lowest four orbitals are filled and the highest orbital (the dx2-y2) is empty, resulting in a large CFSE. These complexes are diamagnetic and tend to be quite stable. With weak field ligands, 3d8 complexes are octahedral and paramagnetic (e.g., [Ni(H2O)6]2+, which has two unpaired electrons in the eg orbitals.
Square planar complexes in catalysis:

Square planar d8 complexes can be oxidized by two electrons to become octahedral (low spin) d6 complexes, which also have a large CFSE. Because the loss of two electrons is accompanied by the gain of two ligands, this process is called oxidative addition. The reverse process is called reductive elimination. Both processes function together in catalytic cycles, such as the hydrogenation of olefins using Wilkinson's catalyst.[10][11] The catalytic cycle is shown at the left.
The catalyst cycles between 4-coordinate Rh(I) (4d8) and 6-coordinate Rh(III) (4d6). The complex first adds H2 oxidatively, to give a six-coordinate complex in which the hydrogen is formally H-. An olefin molecule displaces a solvent molecule, using its π-electrons to coordinate the metal. The complex rearranges by inserting the olefin into the metal-hydrogen bond, a process called migratory insertion. Finally, the complex returns to the square planar geometry by eliminating the hydrogenated olefin (reductive elimination). Wilkinson's catalyst is highly active and is widely used for homogeneous hydrogenation, hydroboration, and hydrosilation reactions.[12][13] With chiral phosphine ligands, the catalyst can hydrogenate prochiral olefins to give enantiomerically pure products.[14] With chiral tridentate ligands that occupy three of the four coordination sites of the square planar complex, very high yields of enantiometrically pure hydrogenation products can be produced. Analogous chiral Ir(I) complexes catalyze the hydrogenation of prochiral ketones to chiral primary alcohols, an important step in the production of many chiral pharmaceutical compounds.[15]
5.7 Jahn-Teller effect[edit | edit source]

The Jahn–Teller effect, sometimes also known as Jahn–Teller distortion, describes the geometrical distortion of molecules and ions that is associated with certain electron configurations. This electronic effect is named after Hermann Arthur Jahn and Edward Teller, who proved, using group theory, that orbitally degenerate molecules cannot be stable.[16] The Jahn–Teller theorem essentially states that any non-linear molecule with a spatially degenerate electronic ground state will undergo a geometrical distortion that removes that degeneracy, because the distortion lowers the overall energy of the molecule.
We can understand this effect in the context of octahedral metal complexes by considering d-electron configurations in which the eg orbital set contains one or three electrons. The most common of these are high spin d4 (e.g., CrF2) , low spin d7 (e.g.,NaNiO2), and d9 (e.g., Cu2+). If the complex can distort to break the symmetry, then one of the (formerly) degenerate eg orbitals will go down in energy and the other will go up. More electrons will occupy the lower orbital than the upper one, resulting in an overall lowering of the electronic energy. A similar distortion can occur in tetrahedral complexes when the t2 orbitals are partially filled. Such geometric distortions that lower the electronic energy are said to be electronically driven. Similar electronically driven distortions occur in one-dimensional chain compounds, where they are called Peierls distortions, and in two-dimensionally bonded sheets, where they are called charge density waves.


The Jahn–Teller effect is most often encountered in octahedral complexes, especially six-coordinate copper(II) complexes.[17] The d9 electronic configuration of this ion gives three electrons in the two degenerate eg orbitals, leading to a doubly degenerate electronic ground state. Such complexes distort along one of the molecular fourfold axes (always labelled the z axis), which has the effect of removing the orbital and electronic degeneracies and lowering the overall energy. The distortion normally takes the form of elongating the bonds to the ligands lying along the z axis, but occasionally occurs as a shortening of these bonds instead (the Jahn–Teller theorem does not predict the direction of the distortion, only the presence of an unstable geometry). When such an elongation occurs, the effect is to lower the electrostatic repulsion between the electron-pair on the Lewis basic ligand and any electrons in orbitals with a z component, thus lowering the energy of the complex. If the undistorted complex would be expected to have an inversion center, this is preserved after the distortion.
In octahedral complexes, the Jahn–Teller effect is most pronounced when an odd number of electrons occupy the eg orbitals. This situation arises in complexes with the configurations d9, low-spin d7 or high-spin d4 complexes, all of which have doubly degenerate ground states. In such compounds the eg orbitals involved in the degeneracy point directly at the ligands, so distortion can result in a large energetic stabilization. Strictly speaking, the effect also occurs when there is a degeneracy due to the electrons in the t2g orbitals (i.e. configurations such as d1 or d2, both of which are triply degenerate). In such cases, however, the effect is much less noticeable, because there is a much smaller lowering of repulsion on taking ligands further away from the t2g orbitals, which do not point directly at the ligands (see the table below). The same is true in tetrahedral complexes (e.g. manganate ([MnO4]2-, d1): the distortion is very subtle because there is less stabilization to be gained when the ligands are not pointing directly at the orbitals.
The expected effects for octahedral coordination are given in the following table:
| Number of d electrons | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| High/Low Spin | HS | LS | HS | LS | HS | LS | HS | LS | ||||||
| Strength of J-T Effect | w | w | s | w | w | w | w | s | s | |||||
w: weak Jahn–Teller effect (t2g orbitals unevenly occupied)
s: strong Jahn–Teller effect expected (eg orbitals unevenly occupied)
blank: no Jahn–Teller effect expected.
The Jahn–Teller effect is manifested in the UV-VIS absorbance spectra of some compounds, where it often causes splitting of bands. It is readily apparent in the structures of many copper(II) complexes.[18] Additional, detailed information about the anisotropy of such complexes and the nature of the ligand binding can be obtained from the fine structure of the low-temperature electron spin resonance spectra.
5.8 Tetrahedral complexes[edit | edit source]
Tetrahedral complexes are formed with late transition metal ions (Co2+, Cu2+, Zn2+, Cd2+) and some early transition metals (Ti4+, Mn2+), especially in situations where the ligands are large. In these cases the small metal ion cannot easily accommodate a coordination number higher than four. Examples of tetrahedal ions and molecules are [CoCl4]2-, [MnCl4]2-, and TiX4 (X = halogen). Tetrahedral coordination is also observed in some oxo-anions such as [FeO4]4-, which exists as discrete anions in the salts Na4FeO4 and Sr2FeO4, and in the neutral oxides RuO4 and OsO4. The metal carbonyl complexes Ni(CO)4 and Co(CO)4]- are also tetrahedral.


The splitting of the d-orbitals in a tetrahedral crystal field can be understood by connecting the vertices of a tetrahedron to form a cube, as shown in the picture at the left. The tetrahedral M-L bonds lie along the body diagonals of the cube. The dz2 and dx2-y2 orbitals point along the cartesian axes, i.e., towards the faces of the cube, and have the least contact with the ligand lone pairs. Therefore these two orbitals form a low energy, doubly degenerate e set. The dxy, dyz, and dxz orbitals point at the edges of the cube and form a triply degenerate t2 set. While the t2 orbitals have more overlap with the ligand orbitals than the e set, they are still weakly interacting compared to the eg orbitals of an octahedral complex.
The resulting crystal field energy diagram is shown at the right. The splitting energy, Δt, is about 4/9 the splitting of an octahedral complex formed with the same ligands. For 3d elements, Δt is thus small compared to the pairing energy and their tetrahedral complexes are always high spin. Note that we have dropped the "g" subscript because the tetrahedron does not have a center of symmetry.
Tetrahedral complexes often have vibrant colors because they lack the center of symmetry that forbids a d-d* transition. Because the low energy transition is allowed, these complexes typically absorb in the visible range and have extinction coefficients that are 1-2 orders of magnitude higher than the those of the corresponding octahedral complexes. An illustration of this effect can be seen in Drierite, which contains particles of colorless, anhydrous calcium sulfate (gypsum) that absorbs moisture from gases. The indicator dye in Drierite is cobalt (II) chloride, which is is a light pink when wet (octahedral) and deep blue when dry (tetrahedral). The reversible hydration reaction is:
- Co[CoCl4] + 12 H2O ⇌ 2 [Co(H2O)6]Cl2
- (deep blue, tetrahedral [CoCl4]2-) (light pink, octahedral [Co(H2O)6]2+)

Drierite Dry and Wet 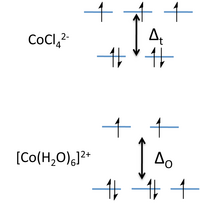
5.9 Stability of transition metal complexes[edit | edit source]
The crystal field stabilization energy (CFSE) is an important factor in the stability of transition metal complexes. Complexes with high CFSE tend to be thermodynamically stable (i.e., they have high values of Ka, the equilibrium constant for metal-ligand association) and are also kinetically inert. They are kinetically inert because ligand substitution requires that they dissociate (lose a ligand), associate (gain a ligand), or interchange (gain and lose ligands at the same time) in the transition state. These distortions in coordination geometry lead to a large activation energy if the CFSE is large, even if the product of the ligand exchange reaction is also a stable complex. For this reason, complexes of Pt4+, Ir3+ (both low spin 5d6), and Pt2+ (square planar 5d8) have very slow ligand exchange rates.
There are two other important factors that contribute to complex stability:
- Hard-soft interactions of metals and ligands (which relate to the energy of complex formation)
- The chelate effect, which is an entropic contributor to complex stability.
Hard-soft interactions
Hard acids are typically small, high charge density cations that are weakly polarizable such as H+, Li+, Na+, Be2+, Mg2+, Al3+, Ti4+, and Cr6+. Electropositive metals in high oxidation states are typically hard acids. These elements are predominantly found in oxide minerals, because O2- is a hard base.
Some hard bases include H2O, OH-, O2-, F-, NO3-, Cl-, and NH3.
The hard acid-base interaction is primarily electrostatic. Complexes of hard acids with hard bases are stable because of the electrostatic component of the CFSE.
Soft acids are large, polarizable, electronegative metal ions in low oxidation states such as Ni0, Hg2+, Cd2+, Cu+, Ag+, and Au+.
Soft bases are anions/neutral bases such as H-, C2H4, CO, PR3, R2S, and CN-). Soft acids typically occur in nature as sulfide or arsenide minerals.
The bonding between soft acids and soft bases is predominantly covalent. For example, metal carbonyls bind through a covalent interaction between a zero- or low-valent metal and neutral CO to form Ni(CO)4, Fe(CO)5, Co(CO)4-, Mn2(CO)10, W(CO)6, and related compounds.
The preference for hard-hard and soft-soft interactions ("like binds like") is nicely illustrated in the properties of the copper halides:
- CuF CuI
- unstable stable
- CuF2 CuI2
- stable unstable
The compounds CuF and CuI2 have never been isolated, and are thermodynamically unstable to disproportionation:
- 2 CuF(s) → Cu(s) + CuF2(s)
- 2 CuI2(s) → 2 CuI(s) + I2(s)
We will learn more about quantifying the energetics of these compounds in Chapter 9.
5.10 Chelate and macrocyclic effects[edit | edit source]

Ligands that contain more than one binding site for a metal ion are called chelating ligands (from the Greek word χηλή, chēlē, meaning "claw"). As the name implies, chelating ligands have high affinity for metal ions relative to ligands with only one binding group (which are called monodentate = "single tooth") ligands.
Consider the two complexation equilibria in aqueous solution, between the cobalt (II) ion, Co2+(aq) and ethylenediamine (en) on the one hand and ammonia, NH3, on the other.
- [Co(H2O)6]2+ + 6 NH3 ⇌ [Co(NH3)6]2+ + 6 H2O (1)
- [Co(H2O)6]2+ + 3 en ⇌ [Co(en)3]2+ + 6 H2O (2)
Electronically, the ammonia and en ligands are very similar, since both bind through N and since the Lewis base strengths of their nitrogen atoms are similar. This means that ΔH° must be very similar for the two reactions, since six Co-N bonds are formed in each case. Interestingly however, we observe that the equilibrium constant is 100,000 times larger for the second reaction than it is for the first.
The big difference between these two reactions is that the second one involves "condensation" of fewer particles to make the complex. This means that the entropy changes for the two reactions are different. The first reaction has a ΔS° value close to zero, because there are the same number of molecules on both sides of the equation. The second one has a positive ΔS° because four molecules come together but seven molecules are produced. The difference between them (ΔΔS°) is about +100 J/mol-K. We can translate this into a ratio of equilibrium constants using:
- Kf(en)/Kf(NH3) = e-ΔΔG°/RT ≈ e+ΔΔS°/R ≈ e12 ≈ 105


The bottom line is that the chelate effect is entropy-driven. It follows that the more binding groups a ligand contains, the more positive the ΔS° and the higher the Kf will be for complex formation. In this regard, the hexadentate ligand ethylenediamine tetraacetic acid (EDTA) is an optimal ligand for making octahedral complexes because it has six binding groups. In basic solutions where all four of the COOH groups are deprotonated, the chelate effect of the EDTA4- ligand is approximately 1015. This means, for a given metal ion, Kf is 1015 times larger for EDTA4- than it would be for the relevant monodentate ligands at the same concentration. EDTA4-tightly binds essentially any 2+, 3+, or 4+ ion in the periodic table, and is a very useful ligand for both analytical applications and separations.
The macrocyclic effect follows the same principle as the chelate effect, but the effect is further enhanced by the cyclic conformation of the ligand. Macrocyclic ligands are not only multi-dentate, but because they are covalently constrained to their cyclic form, they allow less conformational freedom. The ligand is said to be "pre-organized" for binding, and there is little entropy penalty for wrapping it around the metal ion. For example heme b is a tetradentate cyclic ligand which is strongly complexes transition metal ions, including (in biological systems) Fe+2.
Some other common chelating and cyclic ligands are shown below:


Acetylacetonate (acac-, right) is an anionic bidentate ligand that coordinates metal ions through two oxygen atoms. Acac- is a hard base so it prefers hard acid cations. With divalent metal ions, acac- forms neutral, volatile complexes such as Cu(acac)2 and Mo(acac)2 that are useful for chemical vapor deposition (CVD) of metal thin films.
2,2'-Bipyridine and related bidentate ligands such as 1,10-phenanthroline (below, center left) form propeller-shaped complexes with metals such as Ru2+. The [Ru(bpy)3]2+ complex (below left) is photoluminescent and can also undergo photoredox reactions, making it an interesting compound for both photocatalysis and artificial photosynthesis. The chiral propellor shapes of metal polypyridyl complexes such as [Ru(bpy)3]2+ coincidentally match the size and helicity of the major groove of DNA. This has led to a number of interesting studies of electron transfer reactions along the DNA backbone, initiated by photoexcitation of the metal complex.
Crown ethers such as 18-crown-6 (below, center right) are cyclic hard bases that can complex alkali metal cations. Crowns can selectively bind Li+, Na+, or K+ depending on the number of ethylene oxide units in the ring.
- The chelating properties of crown ethers are mimetic of the natural antibiotic valinomycin (below right), which selectively transports K+ ions across bacterial cell membranes, killing the bacterium by dissipating its membrane potential. Like crown ethers, valinomycin is a cyclic hard base.
5.11 Ligand substitution reactions[edit | edit source]
Transition metal complexes can exchange one ligand for another, and these reactions are important in their synthesis, stereochemistry, and catalytic chemistry. The mechanisms of chemical reactions are intimately connected to reaction kinetics. As in organic chemistry, the mechanisms of transition metal reactions are typically inferred from experiments that examine the concentration dependence of the incoming and outgoing ligands on the reaction rate, the detection of intermediates, and the stereochemistry of the reactants and products.
Thermodynamic vs. kinetics. When we think about the reactions of transition metal complexes, it is important to recall the distinction between their thermodynamics and kinetics. Take for example the formation of the square planar tetracyanonickelate complex:
- Ni2+(aq) + 4 CN-(aq) ⇌ [Ni(CN)4]2- (aq) Keq ≈ 1030 M-4
Thermodynamically, [Ni(CN)4]2- is very stable, meaning that the equilibrium above lies very far to the right. Kinetically, however, the complex is labile, meaning that it can exchange its ligands rapidly. For example the exchange between a 13C labeled CN- ion and a bound CN- ligand occurs on the timescale of tens of milliseconds:
- [Ni(CN)4]2- (aq) + *CN-(aq) ⇌ [Ni(CN)3(*CN)]2- + CN-(aq) kexchange ≈ 102 M-1s-1
Conversely, a compound can be thermodynamically unstable but kinetically inert, meaning that it takes a relatively long time to react. For example, the [Co(NH3)6]3+ ion is unstable in acid, but its hydrolysis reaction with concentrated HCl takes about one week to go to completion at room temperature:

- [Co(NH3)6]3+(aq) + 6 H3O+(aq) ⇌ [Co(H2O)6]3+(aq) + 6 NH4+(aq) Keq ≈ 1030
Henry Taube, who studied the mechanisms of ligand exchange reactions in simple test tube experiments, classified transition metal complexes as labile if their reaction half-life was one minute or less, and inert if they took longer to react. The dynamic range of ligand substitution rates is enormous, spanning at least 15 orders of magnitude. On the timescale of most laboratory experiments, the Taube definition of lability is a useful one for classifying reactions into those that have low and high activation energies. As we will see, the crystal field stabilization energy (CFSE) plays a key role in determining the activation energy and therefore the rate of ligand substitution.
Crystal field stabilization energy and ligand exchange rates. Let's consider a very common and simple ligand exchange reaction, which is the substitution of one water molecule for another in an octahedral [M(H2O)6]n+ complex. Since the products (except for the label) are the same as the reactants, we know that ΔG° = 0 and Keq = 1 for this reaction. The progress of the reaction can be monitored by NMR by using isotopically labeled water (typically containing 17O or 18O):

The most striking thing about this (otherwise boring) reaction is the vast difference in rate constants - about 14 orders of magnitude - for different metal ions and oxidation states:
| Mn+ | log k (sec-1) |
|---|---|
| Cr3+ | |
| V2+ | |
| Cr2+ | |
| Cu2+ |

While at first it may seem strange that the same ion in two different oxidation states (Cr3+ vs. Cr2+) would be inert or labile, respectively, we can begin to rationalize the difference by drawing d-orbital splitting diagrams for the complexes. What we find is that octahedral complexes that have high CFSE (Cr3+, V2+) tend to be inert. Conversely, ions with electrons in high energy eg orbitals (Cr2+, Cu2+) tend to be labile. In the case of Cr3+ and V2+, the energy penalty for distorting the complex away from octahedral symmetry - to make, for example, a 5- or 7-coordinate intermediate - is particularly high. This activation energy for ligand substitution is lower for Cr2+ and Cu2+, which already have electrons in antibonding eg orbitals.
Based on the rules we developed for calculating the CFSE of transition metal complexes, we can now predict the trends in ligand substitution rates:
- Octahedral complexes with d3 and d6(low spin) configurations, such as Cr3+ (d3), Co3+ (d6), Rh3+ (d6), Ru2+ (d6), and Os2+ (d6) tend to be substitution-inert because of their high CFSE.
- Square planar d8 complexes, especially those in the 4d and 5d series, are also substitution-inert. Examples are complexes of Pd2+, Pt2+, and Au3+.
- Intermediate cases are complexes of Fe3+, V3+, V2+, Ni2+, and of main group ions (Be2+, Al3+) that are hard Lewis acids. These complexes make strong metal-oxygen bonds and have water exchange rates in the range of 101-106 s-1.
- Ions with zero CFSE exchange water molecules on a timescale of nanoseconds (k ≈ 108-109 s-1). These include ions with d0, d5 (high spin), and d10 electron counts, including alkali metal (Li+, Na+, K+, Rb+, Cs+) and alkali earth (Mg2+, Ca2+, Sr2+, Ba2+) cations, Zn2+, Cd2+, Hg2+, and Mn2+. In these cases the CFSE is zero and the energetic cost of breaking octahedral symmetry is relatively low.
- For p-block elements, faster exchange occurs with larger ions (e.g., Ba2+ > Ca2+ and Ga3+ > Al3+), because Lewis acid strength decreases with increasing ion size.
- The Cu2+ ion (d9), as a Jahn-Teller ion, is already distorted away from octahedral symmetry and is therefore quite labile, exchanging water ligands at a rate of about 108 s-1.
Ligand Substitution Mechanisms. For an MLn complex undergoing ligand substitution, there are essentially three different reaction mechanisms:
- In the dissociative mechanism, a MLn complex first loses a ligand to form an MLn-1 intermediate, and the incoming ligand Y reacts with the MLn-1 fragment:
- L(n-1)M-L* ⇌ L(n-1)M- + L* ⇌ L(n-1)M-Y
This mechanism is illustrated below for ligand substitution on an octahedral ML6 complex. The intermediate state in this example involves a trigonal bipyramidal ML5 fragment as well as free L and Y ligands.

If the rate determining step is the dissociation of L from the complex, then the concentration of Y does not affect the rate of reaction, leading to the first-order rate law:
In the case of an octahedral complex, this reaction would be first order in ML6 and zero order in Y, but only if the highest energy transition state is the one that precedes the formation of the ML5 intermediate. If the two transition states are close in energy (as in the case of the animation at the right), then the rate law becomes more complicated. In this case, we can simplify the problem by assuming a low steady-state concentration of the MLn intermediate. The resulting rate law is:
which reduces to the simpler first-order rate law when k2[Y] >> k-1[L]. Because the formation of the transition state involves dissociation of a ligand, the entropy of activation is always positive in the dissociative mechanism.
- In the associative mechanism, the incoming ligand Y attacks the MLn complex, transiently forming an MLnY intermediate, and the intermediate then loses a ligand L forming the MLn-1Y product.
Complexes that undergo associative substitution are typically either coordinatively unsaturated or contain a ligand that can change its bonding to the metal, e.g. a change in the hapticity or bending of a nitric oxide ligand (NO). In homogeneous catalysis, the associative pathway is desirable because the binding event, and hence the selectivity of the reaction, depends not only on the nature of the metal catalyst but also on the molecule that is involved in the catalytic cycle.

Examples of associative mechanisms are commonly found in the chemistry of d8 square planar metal complexes, e.g. Vaska's complex (IrCl(CO)[P(C6H5)3]2) and tetrachloroplatinate(II). These compounds (ML4) bind the incoming (substituting) ligand Y to form pentacoordinate intermediates ML4Y, which in a subsequent step dissociate one of their ligands. Although the incoming ligand is initially bound at an equatorial site, the Berry pseudorotation provides a low energy pathway for all ligands to sample both the equatorial and axial sites. Ligand dissociation must occur from an equatorial site according to the principle of microscopic reversibility. Dissociation of Y results in no reaction, but dissociation of L results in net substitution, yielding the d8 complex ML3Y. The first step is typically rate determining. Thus, the entropy of activation is negative, which indicates an increase in order in the transition state. Associative reactions follow second order kinetics: the rate of the appearance of product depends on the concentration of both ML4 and Y.

The Trans Effect, which is connected with the associative mechanism, controls the stereochemistry of certain ligand substitution reactions.
The trans effect refers to the labilization (making more reactive) of ligands that are trans to certain other ligands, the latter being referred to as trans-directing ligands. The labilization of trans ligands is attributed to electronic effects and is most notable in square planar complexes, but it can also be observed with octahedral complexes.[19] The cis effect is most often observed in octahedral complexes.
In addition to the kinetic trans effect, trans ligands also have an influence on the ground state of the molecule, the most notable ones being bond lengths and stability. Some authors prefer the term trans influence to distinguish this from the kinetic effect,[20] while others use more specific terms such as structural trans effect or thermodynamic trans effect.[19]
The discovery of the trans effect is attributed to Ilya Ilich Chernyaev,[21] who recognized it and gave it a name in 1926.[22]
The intensity of the trans effect (as measured by the increase in the rate of substitution of the trans ligand) follows this sequence:
- F−, H2O, OH− < NH3 < py < Cl− < Br− < I−, SCN−, NO2−, SC(NH2)2, Ph− < SO32− < PR3, AsR3, SR2, CH3− < H−, NO, CO, CN−, C2H4
Note that weak field ligands tend to be poor trans-directing ligands, whereas strong field ligands are strongly trans-directing.
The classic example of the trans effect is the synthesis of cisplatin and its trans isomer.[23] Starting from PtCl42−, the first NH3 ligand is added to any of the four equivalent positions at random. However, since Cl− has a greater trans effect than NH3, the second NH3 is added trans to a Cl− and therefore cis to the first NH3.
If, on the other hand, one starts from Pt(NH3)42+, the trans product is obtained instead:
The trans effect in square complexes can be explained in terms of the associative mechanism, described above, which goes through a trigonal bipyramidal intermediate. Ligands with a high kinetic trans effect are in general those with high π acidity (as in the case of phosphines) or low-ligand lone-pair–dπ repulsions (as in the case of hydride), which prefer the more π-basic equatorial sites in the intermediate. The second equatorial position is occupied by the incoming ligand. The third and final equatorial site is occupied by the departing trans ligand, so the net result is that the kinetically favored product is the one in which the ligand trans to the one with the largest trans effect is eliminated.[20]
- The interchange mechanism is similar to the associative and dissociative pathways, except that no distinct MLnY or MLn-1 intermediate is formed. This concerted mechanism can be thought of as analogous to nucleophilic substitution via the SN2 pathway at a tetrahedral carbon atom in organic chemistry. The interchange mechanism is further classified as associative (Ia) or dissociative (Id) depending on the relative importance of M-Y and M-L bonding in the transition state. If the transition state is characterized by the formation of a strong M-Y bond, then the mechanism is Ia. Conversely, if weakening of the M-L bond is more important in reaching the transition state, then the mechanism is Id.
An example of the Ia mechanism is the interchange of bulk and coordinated water in [V(H2O)6]2+. In contrast, the slightly more compact ion [Ni(H2O)6]2+ ion exchanges water via the Id mechanism.[24]
Effects of ion pairing. Highly charged cationic complexes tend to form ion pairs with anionic ligands, and these ion pairs often undergo reactions via the Ia pathway. The electrostatically held nucleophilic incoming ligand can exchange positions with a ligand in the first coordination sphere, resulting in net substitution. An illustrative process is the "anation" (reaction with an anion) of the chromium(III) hexaaquo complex:
- [Cr(H2O)6]3+ + SCN− ⇌ {[Cr(H2O)6], NCS}2+
- {[Cr(H2O)6], NCS}2+ ⇌ [Cr(H2O)5NCS]2+ + H2O
5.12 Discussion questions[edit | edit source]
- Discuss chelating ligands and what they do, using some new examples.
- Explain (using some new examples) how we know if an octahedral complex of a metal ion will be high spin or low spin, and what measurements we can do to confirm it.
5.13 Problems[edit | edit source]
1. Predict the molecular geometry of the following complexes, and determine whether each will be diamagnetic or paramagnetic:
(a) [Fe(CN)6]4-
(b) [Fe(C2O4)3]4-
(c) [Zn(NH3)4]2+
(d) [Mo(CO)6]
(e) [Rh(NH3)4]+
2. For each of the following transition metal complexes, give (i) the d-electron count), (ii) the approximate molecular geometry of the complex, and (iii) an energy level diagram showing the splitting and filling of the d-orbitals.
(a)[Os(CN)6]3-
(b)cis-PtCl2(NH3)2
(c) [Cu(NH3)4]+
3. Tetrahedral complexes are almost always high spin, whereas octahedral complexes can be either high or low spin. Explain.
4. For each of the Mn complexes in the table below, give electronic configurations (within the t2g and eg sets of 3d orbitals) that are consistent with the observed magnetic moments.
| Compound | µ (BM) |
|---|---|
| [Mn(CN)6]4- | 1.8 |
| [Mn(CN)6]3- | 3.2 |
| [Mn(NCS)6]4- | 6.1 |
| [Mn(acac)3] | 5.0 |
5. For each of the following pairs, identify the complex with the higher crystal field stabilization energy (and show your work).
(a) [Fe(CN)6]3- vs. [Fe(CN)6]4-
(b) [Ni(NH3)6]2+ vs. [Cd(en)2]2+, where en = H2NCH2CH2NH2
(c) Mn(H2O)6]2+ vs. [PdCl4]2-
6. In a solution made by combining FeCl3 with excess ethylenediaminetetraacetic acid (EDTA) at neutral pH, the concentration of Fe3+(aq) ions is on the order of 10-17 M. However, in a solution of ethylenediamine and acetic acid at comparable concentration, the Fe3+(aq) concentration is about 10-7, i.e., 1010 times higher. Explain.
7. The complex [Ti(H2O)6]3+ is violet, while the analogous complex with another monodentate neutral ligand L, [Ti(L)6]3+ is orange. How many of the following statements are true? Explain briefly.
(a) L is a stronger field ligand than H2O.
(b) [Ti(L)6]3+ is a high-spin complex.
(c) [Ti(L)6]3+ absorbs yellow and red light.
(d) Both complexes have two 3d electrons associated with the metal.
8. OH- and CN- are both Brønsted bases, and both can form complexes with metal ions. Explain how OH- can be a much stronger Brønsted base than CN-, and at the same time much lower in the spectrochemical series.
9. A solution of [Ni(H2O)6]2+ is faint green and paramagnetic (µ = 2.90 BM), whereas a solution of [Ni(CN)4]2- is yellow and diamagnetic.
(a) Draw the molecular geometry and the d-orbital energy level diagrams for each complex, showing the electronic occupancy of the d-orbitals.
(b) Explain the differences in magnetism and color.
10. W. Deng and K. W. Hipps (J. Phys. Chem. B 2003, 107, 10736-10740) reported an STM study of the electronic properties of Ni(II)tetraphenyl porphyrin (NiTPP), a red-purple, neutral diamagnetic complex that is made by reacting Ni(II) perchlorate with tetraphenylporphine. When NiTPP is reacted with sodium thiocyanate it forms another complex that is paramagnetic. Draw the structures of NiTPP and the product complex, and the crystal field energy level diagram that explains each. What value of the magnetic moment (in units of μB) would you expect for the paramagnetic complex?

11. One of the simplest reactions a coordination complex can do is ligand exchange. For example, metal aquo complexes can exchange a coordinated water molecule with a free (solvent) water molecule, and the rate of the reaction can be measured by isotope labeling, NMR, and other techniques. Interestingly, these rates vary widely for water exchange with different metal ions - over a range of 14 orders of magnitude - as shown in the figure at the right. For some metal ions, the rate is so slow that it takes weeks for one water molecule to exchange for another. In other cases, the timescale of the exchange is nanoseconds.
(a) There is an overall trend in which the rate of exchange decreases as the oxidation state of the metal increases. Explain this trend in terms of crystal field stabilization energy (CFSE). How is the CFSE related to the activation energy of the water exchange reaction?
(b) Explain any trends you observe for the rate of water exchange among divalent metal ions.
(c) Cu2+ has an anomalously fast ligand exchange rate. Why?
(d) What are the geometries and d-electron counts of the aquo complexes of the slowest divalent, trivalent, and tetravalent metal ions in the figure? Do they have particularly high or low CFSE's? Explain.
12. Ligand exchange rates for main group ions increase going down a group, e.g., Al3+ < Ga3+ < In3+. For transition metal ions, we see the opposite trend, e.g., Fe2+ > Ru2+ > Os2+. Explain why these trends are different.
13. Seppelt and coworkers reported the very unusual ion [AuXe4]2+ in the salt [AuXe4]2+ (Sb2F11-)2 (Science 2000, 290, 117-118). This was the first report of a compound containing a bond between a metal and a noble gas atom. Draw a d-orbital energy diagram for this ion and predict whether it should be diamagnetic or paramagnetic. Would you expect to be able to form a similar complex using Cu in place of Au, or Kr in place of Xe? Why or why not?
14. For the reaction cis-Mo(CO)4L2 + CO → Mo(CO)5L + L, the reaction rate is found to vary by a factor of 500 for two different ligands L, but it is relatively insensitive to the pressure of CO gas. (a) What kind of mechanism does this reaction have? (b) What are the signs of the activation volume and the activation entropy?
15. In Rosenberg's initial discovery of the biological effects of cis-Pt(NH3)2Cl2, the compound was made accidentally by partial dissolution of a Pt anode in an electrolyte solution that contained glucose and magnesium chloride.[25] The electrolysis reaction also produced small amounts of ammonium ions. Explain mechanistically why the cis-isomer is formed selectively under these conditions.
5.14 References[edit | edit source]
- ↑ Rosi, Nathaniel L.; Eckert, Juergen; Eddaoudi, Mohamed; Vodak, David T.; Kim, Jaheon; O'Keefe, Michael; Yaghi, Omar M. (2003). "Hydrogen storage in microporous metal-organic frameworks". Science. 300 (5622): 1127–1129. Bibcode:2003Sci...300.1127R. doi:10.1126/science.1083440. PMID 12750515.
- ↑ Green, M.L.H. (1995). "A new approach to the formal classification of covalent compounds of the elements". Journal of Organometallic Chemistry. 500: 127–148. doi:10.1016/0022-328X(95)00508-N.
- ↑ The CBC Method, Parkin group, Columbia University.
- ↑ Crabtree, Robert. The Organometallic Chemistry of the Transition Metals:4th edition. Wiley-Interscience, 2005
- ↑ "Metal–Ligand Multiple Bonds: The Chemistry of Transition Metal Complexes Containing Oxo, Nitrido, Imido, Alkylidene, or Alkylidyne Ligands" W. A. Nugent and J. M. Mayer; Wiley-Interscience, New York, 1988.
- ↑ McConville, David H.; Wolf, Jennifer R.; Schrock, Richard R. (1993). "Synthesis of chiral molybdenum ROMP initiators and all-cis highly tactic poly(2,3-(R)2norbornadiene) (R = CF3 or CO2Me)". J. Am. Chem. Soc. 115 (10): 4413–4414. doi:10.1021/ja00063a090.
- ↑ Nguyen, Sonbinh T.; Johnson, Lynda K.; Grubbs, Robert H.; Ziller, Joseph W. (1992). "Ring-opening metathesis polymerization (ROMP) of norbornene by a Group VIII carbene complex in protic media". J. Am. Chem. Soc. 114 (10): 3974–3975. doi:10.1021/ja00036a053.
- ↑ Rosenberg B, Vancamp L, Trosco JE, Mansour VH (1969). "Platinum compounds - a new class of potent antitumour agents". Nature. 222 (5191): 385–386. doi:10.1038/222385a0.
{{cite journal}}: CS1 maint: uses authors parameter (link) - ↑ G. Wilkinson, M. Rosenblum, M. C. Whiting, R. B. Woodward (1952). "The Structure of Iron Bis-Cyclopentadienyl". Journal of the American Chemical Society. 74 (8): 2125–2126. doi:10.1021/ja01128a527.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Osborn, J. A.; Jardine, F. H.; Young, J. F.; Wilkinson, G. (1966). "The Preparation and Properties of Tris(triphenylphosphine)halogenorhodium(I) and Some Reactions Thereof Including Catalytic Homogeneous Hydrogenation of Olefins and Acetylenes and Their Derivatives". Journal of the Chemical Society A: 1711–1732. doi:10.1039/J19660001711.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ "Tris(triphenylphosphine)halorhodium(I)" J. A. Osborn, G. Wilkinson, Inorganic Syntheses, 1967, Volume 10, p. 67. DOI 10.1002/9780470132418.ch12
- ↑ D. A. Evans, G. C. Fu and A. H. Hoveyda (1988). "Rhodium(I)-catalyzed hydroboration of olefins. The documentation of regio- and stereochemical control in cyclic and acyclic systems". J. Am. Chem. Soc. 110 (20): 6917–6918. doi:10.1021/ja00228a068.
- ↑ I. Ojima, T. Kogure (1972). "Selective reduction of α,β-unsaturated terpene carbonyl compounds using hydrosilane-rhodium(I) complex combinations". Tetrahedron Lett. 13 (49): 5035–5038. doi:10.1016/S0040-4039(01)85162-5.
- ↑ W. S. Knowles (2003). "Asymmetric Hydrogenations (Nobel Lecture 2001)". Advanced Synthesis and Catalysis. 345 (12): 3–13. doi:10.1002/adsc.200390028.
- ↑ J. Yu, J. Long, W. Wu., P. Xue, and X. Zhang (2017). "Iridium-Catalyzed Asymmetric Hydrogenation of Ketones with Accessible and Modular Ferrocene-Based Amino-phosphine Acid (f-Ampha) Ligands". Organic Letters. 19 (3): 690–693. doi:10.1021/acs.orglett.6b03862.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ H. Jahn and E. Teller (1937). "Stability of Polyatomic Molecules in Degenerate Electronic States. I. Orbital Degeneracy". Proceedings of the Royal Society A. 161 (905): 220–235. Bibcode:1937RSPSA.161..220J. doi:10.1098/rspa.1937.0142.
- ↑ Rob Janes and Elaine A. Moore (2004). Metal-ligand bonding. Royal Society of Chemistry. ISBN 0-85404-979-7.
- ↑ Patrick Frank, Maurizio Benfatto, Robert K. Szilagyi, Paola D'Angelo, Stefano Della Longa, and Keith O. Hodgson "The Solution Structure of [Cu(aq)]2+ and Its Implications for Rack-Induced Bonding in Blue Copper Protein Active Sites" Inorganic Chemistry 2005, vol 44, pp 1922–1933. DOI 10.1021/ic0400639
- ↑ a b Coe, B. J.; Glenwright, S. J. Trans-effects in octahedral transition metal complexes. Coordination Chemistry Reviews 2000, 203, 5-80.
- ↑ a b Robert H. Crabtree (2005). The Organometallic Chemistry of the Transition Metals (4th ed.). New Jersey: Wiley-Interscience. ISBN 0-471-66256-9.
- ↑ Kauffmann, G. B. I'lya I'lich Chernyaev (1893-1966) and the Trans Effect. J. Chem. Educ. 1977, 54, 86-89.
- ↑ Chernyaev, I. I. The mononitrites of bivalent platinum. I. Ann. inst. platine (USSR) 1926, 4, 243-275.
- ↑ George B. Kauffman, Dwaine O. Cowan (1963). "cis- and trans-Dichlorodiammineplatinum(II)". Inorg. Synth. 7: 239–245. doi:10.1002/9780470132388.ch63.
{{cite journal}}: CS1 maint: uses authors parameter (link) - ↑ Helm, Lothar; Merbach, André E. (2005). "Inorganic and Bioinorganic Solvent Exchange Mechanisms". Chem. Rev. 105 (6): 1923–1959. doi:10.1021/cr030726o. PMID 15941206.
- ↑ Rosenberg, B.; Van Camp, L.; Krigas, T. (1965). "Inhibition of Cell Division in Escherichia coli by Electrolysis Products from a Platinum Electrode". Nature. 205 (4972): 698–9. doi:10.1038/205698a0. PMID 14287410.











![{\displaystyle {\ce {Rate={{\mathit {k}}_{1}[ML_{\mathit {n}}]}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f19546a5039b36de5f4c4fd594797bc0df9b999)
![{\displaystyle {\ce {Rate}}={\frac {k_{1}k_{2}[{\ce {Y}}][{\ce {ML_{\mathit {n}}}}]}{{k_{-1}[{\ce {L}}]}+k_{2}[{\ce {Y}}]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccc9e0dfadba0e61ce35c386afdc89e901198c08)

