Introduction to Inorganic Chemistry/Basic Science of Nanomaterials

  Basic Science of Nanomaterials

            

What do stained glass, sunscreen, magnetic hard drives, heterogeneous catalysts, consumer electronics, stain-resistant clothing, self-cleaning glass, and medical diagnostics all have in common? All of them derive some special property and utility from nanoscale materials: ordinary elements and inorganic compounds such as gold, silver, TiO₂, chromium, SiO₂, and silicon that acquire different properties when their characteristic dimensions are somewhere between 1 and 100 nm. In this chapter we will learn about the basic science of nanomaterials, i.e., what it is about their size that makes them different.

Learning goals for Chapter 11:

• Understand the physical basis of mesoscopic behavior in nanoscale semiconducting and magnetic particles.
• Describe how the particle-in-a-box equation applies to electrons in quantum wells.
• Use the Brus formula to calculate the band gap energy of nanoscale semiconductor particles.
• Use the surface energy concept to calculate changes in the melting point and vapor pressure of nanoparticles.
• Describe the methods used to make semiconducting and metal nanocrystals of uniform size.
• Explain the origin of the localized surface plasmon resonance effect in metal nanoparticles.
• Describe the emerging analytical and biomedical applications of metal nanoparticles.

  11.1 Physics and length scales: cavity laser, Coulomb blockade, nanoscale magnets

The special properties of nanomaterials do not derive from different laws of physics, which are the same for objects large and small. For example, Newton's second law (F = ma), Coulomb's law (E = q₁q₂/4πε₀r), and the laws of energy and momentum conservation are the same for buckyballs (C₆₀) and full-size soccer balls. Nevertheless, the physics of electrons, atoms, and photons naturally produce characteristic length scales, some of which we have already seen. For example, in Chapter 6 we discovered that the mean free path of an electron in a good metal is about 40 nm. In Chapter 10, we learned that the Bohr radius of an electron or hole in doped Si is about 4 nm, and that the coherence length of Cooper pairs in semiconductors is somewhere between a few nm and 1 µm. When objects become small relative to these characteristic lengths, their physical properties change in interesting ways. Materials that exist at the relevant length scale are called mesoscopic (meso = "between," scopic = "size") meaning that they cross over from one kind of behavior - the bulk behavior of large objects - to another. This length scale is different for different kinds of properties, but for many it happens between 1 and 100 nm. We illustrate this point with a few examples.

A VCSEL device structure. This is a bottom-emitting multiple-quantum-well VCSEL.

The cavity laser. A vertical cavity surface-emitting laser (or VCSEL) is a semiconductor-based device that emits light in the vertical direction relative to the plane of the chip. These devices are being developed and used for high power applications such as laser surgery, infrared illumination for military surveillance, and laser cutting tools. The basic design of a VCSEL is shown at the right. The VCSEL is basically a light-emitting diode, incorporating p-type and n-type regions of the III-V semiconductor (Al,Ga)As. However, it has two special features. First, the refractive index of the semiconductor is modulated above and below the junction to make Bragg mirrors. These mirrors reflect light emitted in the junction, so that the photon density becomes very high there, a necessary condition for stimulated emission and lasing. The Bragg mirror stack is asymmetric (thinner on the bottom), so that light can escape from the junction in one direction only. Second, the junction itself consists of a thin "quantum well" layer of (In,Ga)As, a III-V semiconductor with a smaller band gap than the surrounding (Al,Ga)As layers.

The quantum well structure, the band diagram of which is illustrated at the left, is the nanoscale part of the laser. The energies of the conduction and valence bands of (Al,Ga)As flank those of the thin (In,Ga)As layer. Therefore, electrons and holes injected into that layer cannot escape: electrons in (In,Ga)As do not have enough energy to climb "up" to the conduction band of (Al,Ga)As and holes cannot climb "down." Electrons confined to such a small well behave as a particle-in-a-box (as we learned in the context of electrides in Chapter 9).
The electron has a kinetic energy defined by the equation:

$KE={\frac {h^{2}n^{2}}{8mL^{2}}}$

We can calculate the energy difference between the lowest (n=1) and next lowest (n=2) levels, which is inversely proportional to the square of the thickness (L) of the (In,Ga)As layer. In this calculation we need to use the effective mass of the electron in (In,Ga)As, which is about 7% of the electron rest mass. With an 8 nm thick layer, this energy is:

$E={\frac {(2^{2}-1^{2})(6.626\cdot 10^{-34}Js)^{2}}{8\cdot 0.07\cdot (9.1\cdot 10^{-31}kg)(8\cdot 10^{-9}m)^{2}}}=4.0\cdot 10^{-20}J=0.25eV$

The VCSEL cavity will thus have a resonant energy of 0.25 eV and emit photons at this energy in the infrared (λ ≈ 5000 nm). Note that because of the inverse square dependence of the cavity energy on layer thickness, lasers based on this design can only function at nanoscale dimensions. When the cavity is three times thicker, its resonant energy becomes comparable to the thermal energy at room temperature (kT = 0.026 eV), and the lasing effect is thermally "washed out."

Basic design of a parallel plate capacitor of area A and with a dielectric thickness of d

Coulomb blockade. A capacitor is a (macroscopic) device that stores electrical charge. The basic structure of a capacitor is shown at the right. When a voltage is applied to such a device, it develops a charge (± Q) on the two plates that is proportional to the voltage:

$C={\frac {Q}{V}}$

The magnitude of the capacitance C is determined by the permittivity ε and the dimensions of the dielectric layer, A and d.

$C={\frac {\varepsilon A}{d}}$

We can also calculate the work done in charging the capacitor up (i.e., the energy stored by charging the capacitor) by integrating the voltage times the charge:

Schematic of a single-electron transistor.

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/en.wikibooks.org/v1/":): {\displaystyle E = \int_0^Q V(q) \mathrm{d}q = \int_0^Q \frac{q}{C} \mathrm{d}q = {1 \over 2} {Q^2 \over C} = {1 \over 2} C V^2 = {1 \over 2} VQ}

Now it is interesting to ask, what happens to a capacitor when we make it very small? This is of particular interest in a device called a single electron transistor, a schematic diagram of which is shown at the right. The metallic gate lead is separated from a "quantum dot," which can be a metal or semiconductor particle, by a thin dielectric layer. This metal-dielectric-metal sandwich acts as a capacitor, and from the equation above, the energy needed to charge it by a single electron (Q = e) is:

$E={\frac {e^{2}}{2C}}$

where e is the charge of the electron, 1.602 x 10^-19 Coulomb. If the gate width and lateral dimensions are very small - say 2 nm as is readily achievable in self-assembled Coulomb blockade devices - then for a typical insulating dielectric, a voltage of about 200 mV is needed to charge the quantum dot by a single electron. Again, this effect is unique to the nanoscale, because a 10 times larger device area would make the single-electron charging voltage about 20 mV, which is smaller than the thermal energy kT (26 meV). Thus for devices larger than about 5-6 nm, individual electron charging events are washed out at room temperature by thermal fluctuations.

How can a nanoscale capacitor like this act as a transistor, which functions as a switch in an electrical circuit? The effect comes from the mutual repulsion of electrons. An electron on the quantum dot repels any other electron that would be forced onto it by applying a small voltage between the source and the drain. Hence the conductance of the quantum dot is very low at a gate bias of zero volts, or at any gate bias (200, 400, 600 mV...) that places an integer number (1, 2, 3,...) of electrons on the dot. But halfway in between these voltages (e.g., at 100, 300, 500 mV) the energy is the same whether there are n or n+1 electrons on the dot. This means that electrons can hop on and off without changing their energy, i.e., they can tunnel through the dot from source to drain. This effect gives peaks in the conductance of the dot at regular steps in the gate voltage. In effect, the gate can act as a switch, as in a conventional field-effect transistor. Single-electron transistors are being researched as ultra-sensitive electrometers and single-molecule chemical sensors, since a tiny change in the electrostatic environment of the dot can switch the device on or off.

Longitudinal and perpendicular recording, two types of writing heads on a hard disk.

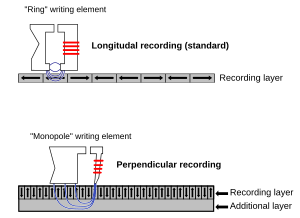
Nanoscale magnets. Ferro- and ferrimagnetic materials such as iron and chromium oxide are used for digitial storage of information in hard disks. The individual memory bits, which can be oriented perpendicular or parallel to the plane of the disk as shown at the right, store a logical "0" or "1" depending on the orientation of their magnetic dipole. To be useful, this information must be non-volatile, i.e., the magnetic bit must retain its polarization in the absence of an applied field from the read/write head.

The storage density of such magnetic memories is impressive. A 2.5" hard drive can now store 1 TB of information, using rod-shaped magnetic grains that are approximately 0.5 µm long. We now have good synthetic methods for making these same materials as crystals with dimensions of only a few nanometers. Why aren't those nanocrystals used to make even more dense memory disks?

A ferrofluid containing superparamagnetic Fe₃O₄ nanoparticles, which are coated with oleic acid and suspended in oil, in the field of a strong permanent magnet.

The reason is that the energy needed to flip the magnetization (i.e., to turn a "0" into a "1" and vice-versa) is strongly size-dependent. For a ferro- or ferrimagnet this energy is equal to Mr³, where M is the magnetic energy per unit volume and r is the characteristic dimension (e.g., the length of the edge of a cube, or the diameter of a sphere) of the magnetic grain. For typical materials such as iron, this energy becomes comparable to kT when r is about 3-5 nm. Such small particles are superparamagnetic, meaning that they still have a large magnetic moment because of the ordering of their spins, but they do not retain a permanent polarization in the absence of an applied magnetic field. Superparamagnetic particles are thus not useful for magnetic memories, but they are interesting and practical in other ways, for example in ferrofluids, magnetic resonance imaging (MRI), and some emerging medical diagnostic and therapeutic applications.

In these three illustrative examples (involving light emission, electronic conduction, and magnetic behavior), the transition to new properties involves a crossover in which the characteristic energy of the system is comparable to the thermal energy kT. It just so happens that for many physical phenomena, this crossover occurs on the length scale of nanometers.

  11.2 Semiconductor quantum dots

Atomic resolution image of a CdSe nanoparticle.

Emission colors of CdSe nanoparticles of different sizes. Smaller particles emit blue light because the exciton energy increases as the size decreases.

One of the most fascinating and well-studied mesoscopic effects occurs with semiconductor particles of various shapes when one or more of their dimensions is in the range of a few nanometers. These so-called "quantum dots" (0D), "quantum rods" (1D) and "nanosheets" (2D) acquire striking new electronic and optical properties.

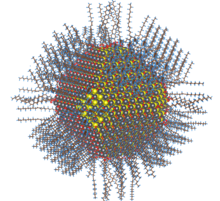
The synthesis of semiconductor quantum dots, which is discussed in more detail below, is sufficiently well controlled to give essentially perfect crystals of a few thousand atoms, something that is statistically impossible in a macroscopic crystal. An image of such a crystal is shown at the right. In the synthesis, these crystals can be capped with an epitaxial layer of ligands or by a shell of a wider bandgap semiconductor (such as ZnS in the case of CdSe), so that the inner core is effectively a quantum well. Electron-hole pairs formed by excitation of the core semiconductor are confined there and cannot reach the external surface of the particle, where they might otherwise be trapped and recombine thermally. Consequently, the quantum yield for bandgap emission of semiconductor quantum dots is typically high, giving rise to the bright emission colors shown at the right for CdSe particles of different sizes. Because of their strong and narrow emission bands, quantum dots are of interest as luminescent tags for biological imaging applications, and also as light absorbers and emitters in solar cells and optical displays. The bright photoluminescence of semiconductor core-shell quantum dots is the basis of commercial television displays, which can be manufactured in larger and brighter formats than organic light emitting diode (OLED) displays.

The size-dependence of the emission color comes primarily from a particle-in-a-box effect. The electron and hole that are created when the quantum dot absorbs light are bound together as an exciton by the confines of the "box". Louis Brus used first-order perturbation theory to determine that the bandgap of a semiconductor quantum dot is given approximately by:

$E_{gap}=E_{gap,bulk}+{\frac {{h}^{2}}{8\mu {{R}^{2}}}}-{\frac {1.8{e}^{2}}{4R\pi \varepsilon {{\varepsilon }_{0}}}}+...$

where R is the particle radius, µ is the electron-hole reduced mass (1/µ = 1/m_e* + 1/m_h*), m_e* and m_h* are the electron and hole effective masses, and ε is the dielectric constant of the semiconductor. In this equation, the first term after the bulk bandgap is the kinetic energy due to confinement of the exciton, and the second term represents the electrostatic attractive energy between the confined electron and hole. Because the energy is a function of R², it can be widely tuned across the visible spectrum by changing the size of the quantum dot.

  11.3 Synthesis of semiconductor nanocrystals

Complete atomistic model of a 5 nm diameter colloidal lead sulfide nanoparticle with surface passivation by oleic acid, oleyl and hydroxyl groups.

Early work on the quantum size effect in semiconductor nanoparticles used simple metathesis reactions in the synthesis. For example, CdSe and PbS can be precipitated at ambient temperature by the reactions:

CdCl₂(aq) + H₂Se(g) = CdSe (s) + 2 HCl(aq)

Pb(NO₃)₂ + H₂S(g) = PbS(s) + 2 HNO₃(aq)

The growth of the particles was restricted by carrying out these reactions in different matrices, such as in polymer films or the silicate cages of zeolites, and capping ligands were also sometimes used to limit particle growth. While these reactions did produce nanoparticles, in general a broad distribution of particle sizes was obtained. The particles were also unstable to Ostwald ripening - in which large particles grow at the expense of smaller ones in order to minimize the total surface energy - because of the reversibility of the acid-forming synthetic reactions in aqueous media. The lack of good samples prevented detailed studies and the development of applications for semiconductor quantum dots.

A very important development in nanoparticle synthesis came in the early 1990's, when Murray, Norris, and Bawendi introduced the first non-aqueous, controlled growth process for II-VI semiconductor quantum dots. The keys to this synthesis were (1) to use non-aqueous solvents and capping ligands to stabilize the products against ripening, (2) to carry out the reaction at high temperature to ensure good crystallinity, and (3) to separate the steps of particle nucleation and growth, and thereby obtain particles of uniform size. This procedure is illustrated below:

The synthesis is carried out in a coordinating, high boiling solvent that is a mixture of trioctylphosphine (TOP) and trioctylphosphine oxide (TOPO). In early experiments, organometallic cadmium compounds such as diethylcadmium were used as the metal source, but it was later found that these highly toxic and pyrophoric compounds could be replaced by CdO. At the start of the reaction, a selenium source, typically bis(trimethylsilyl)selenium, [(CH₃)₃Si]₂Se, dissolved in TOP is rapidly injected into the hot (350 °C) reaction mixture. The reaction causes a rapid burst of nanoparticle nucleation, but the temperature also drops as the cold solvent is injected and so the nucleation event ends quickly. The cooled solution now contains nanocrystal seeds. It is supersaturated in TOPO-Cd and TOP-Se, but particle growth proceeds slowly until the solution is heated again to the growth temperature, ca. 250°C. Particle growth and size-focusing occurs because small particles require less added material to grow by an amount ΔR than larger particles. This is because the volume of an added shell around a spherical seed is 4πR²ΔR, so for larger R, ΔR is smaller. Very narrow particle size distributions can be obtained under conditions of high supersaturation, where the rate of nanoparticle growth is fast relative to particle dissolution and Ostwald ripening. The size distribution can then be narrowed further by adding a non-solvent such as hexane to the cooled reaction mixture. The largest particles precipitate first, followed by smaller particles. Because the nanoparticles are capped with a ligand shell of TOP, they can be re-suspended in organic solvents once they are size-separated.

The high temperature synthesis of semiconductor quantum dots has been applied to a broad variety of materials including II-VI, III-V, and IV-VI semiconductors. Monodisperse nanoparticles of controlled shapes can be made by variants of this method. For example, it is possible to adjust the conditions so that CdSe nucleates in the zincblende polymorph as tetrahedrally shaped seeds, and then grow polar wurtzite "arms" onto each triangular face, resulting in nanocrystal tetrapods. Numerous other nanocrystal shapes such as rods, arrowheads, rice (tapered rods), and polar structures such as Janus rods can be made by variants of this technique. These shape-control strategies often involve the use of ligands that adsorb specifically to certain crystal faces and inhibit their growth. For example, hexylphosphonic acid ligands adsorb selectively to Cd-rich crystal faces and thus lead to the growth of prismatic wurtzite-phase CdSe nanocrytals.

Epitaxial growth of silicon nanowires catalyzed by gold nanoparticles in the vapor-liquid-solid (VLS) process.

A second widely used method of semiconductor nanocrystal synthesis involves growth from molecular precursors and molten metal droplets, as shown in the figure at the right. The vapor-liquid-solid (VLS) and related solution-liquid-solid (SLS) growth processes rely on the fact that semiconductors such as Si, Ge, GaAs, InP, and others are soluble at high temperatures in liquid metals such as Au and Cu. The catalytic reduction of a molecule such as silicon tetrachloride (SiCl₄) at the surface of a gold nanocrystal liberates HCl gas and creates a solid solution of Si in Au. The presence of Si lowers the melting point of Au, and as more SiCl₄ reacts, a liquid eutectic droplet of the Si-Au alloy is formed. When this droplet becomes supersaturated in Si, a silicon nanocrystal nucleates and grows. This reaction can be performed on the surface of a macroscopic Si crystal, in which case nanocrystal "whiskers" grow from the surface, typically as single crystals and with an epitaxial orientation that is determined by the Si crystal face of the substrate. The diameter of the whiskers is controlled by the radius of the Au drops, which can be as small as a few nanometers and as large as several microns. Using this technique, "forests" of nanowires or microwires can be grown. Because the composition of the nanowire depends on the precursor being fed to the Au droplets, it is possible to make "totem pole" structures with varied compositions along the nanowire axis. Semiconductor shells can also be grown around the wires by chemical vapor deposition (CVD). The VLS process can also be adapted to complex compositions for which no molecular precursor is available by using a laser to ablate the semiconductor from a solid target.

Semiconductor nanowires made by this method are the basis of extremely sensitive biosensors, in which a molecular binding event anywhere along the wire strongly affects its electrical conductivity. Nanowire and microwire arrays are also being studied as solar cell and lithium battery materials, as well as nanoscale electronic and optoelectronic devices.

  11.4 Surface energy

Nanoparticles have a substantial fraction of their atoms on the surface, as shown in the plot at the right. This high surface area to volume ratio is an important factor in many of the physical properties of nanoparticles, such as their melting point and vapor pressure, and also in their reactivity. Heterogeneous catalysts, for example, are often based on nanoparticles because the catalytically reactive atoms are those that are on the surface of the particle.

The surface energy is always positive. A key quantity that is connected with the chemistry of all surfaces is the surface energy. This is the (thermodynamically unfavorable) energy of making "dangling bonds" at the surface. Atoms at the surface are under-coordinated, and because breaking bonds costs energy, surface atoms always have higher energy than atoms in the bulk. This happens regardless of whether the bonding is covalent (as in a metal), ionic (in a salt), or non-covalent (in a liquid such as water). We see this effect, for example, in water droplets that bead up on a waxy surface. The droplet contracts into a sphere (against the force of gravity that works to flatten it) in order to minimize the number of dangling hydrogen bonds at the surface.

In the case of metal or semiconductor particles, strong covalent bonds are broken at the surface. For example, a gold atom in bulk face-centered cubic Au has 12 nearest neighbors, but a gold atom on the (111) surface of the crystal (the most dense crystal plane of gold) has six nearest neighbors in-plane and three underneath, for a total of 9. We might expect the surface energy of this crystal face to be a little less (because the remaining bonds will become slightly stronger) than 3/12 = 1/4 of the bonding energy of bulk Au, and this is in fact a fairly good rule of thumb for many materials. When translated into energy per unit area, the surface energy of metals and inorganic salts is usually in the range of 1-2 J/m².

Example: The sublimation energy of bulk gold is 334 kJ/mol, and the surface energy is 1.5 J/m². What percentage of the bulk bonding energy is lost by atoms at the (111) surface of a gold crystal?

To solve this problem, we need to know the surface area per Au atom. Gold has the face-centered cubic structure, and the unit cell edge length is 4.08 Å. From this we can determine that the Au-Au distance is 4.08/1.414 = 2.88 Å. In a hexagonal array of gold atoms with this interatomic spacing, the surface area per atom is (2.88 Å)² x 0.866 = 7.2 Ų. Multiplying by Avogadro's number, we find that the area per mole of Au surface atoms on the (111) crystal face is 4.3 x 10⁴ m².

Now we multiply this area by the surface energy:

(4.3 x 10⁴ m²/mol) x (1.5 J/mol) x (1 kJ/1000 J) = +65 kJ per mole of Au surface atoms.

65 kJ/334 kJ x 100% = 19% of the bulk bonding energy is lost by atoms at the surface.

It is clear from this example that the surface energy of nanoparticles can have a major effect on their physical properties, since a large fraction of the atoms in a nanoparticle are on the surface. A good example of this is the dramatic depression of the melting point.

Solid nanocrystals are in general faceted, whereas liquid droplets made by melting nanocrystals adopt a spherical shape to minimize the surface area.

A faceted solid nanocrystal melts into a spherical droplet in order to minimize its surface energy.

Let's consider melting a silver nanocrystal that is 2 nm in diameter, meaning that about 1/2 of the atoms are on the surface. The spherical liquid droplet has lower surface area than the faceted crystal. For example, a cube has 1.24 times the surface area of a sphere of the same volume. If the decrease in surface area is about 20% upon melting, and the surface energy is about 1/4 of the bulk bonding energy of the atoms, then for a 2 nm diameter nanocrystal we would estimate that:

ΔH°_fusion ≈ ΔH°_{fusion, bulk} - (1/2)(0.25)(1/4)ΔH°_vap = ΔH°_{fusion, bulk} - 0.025 ΔH°_{vap, bulk}

where ΔH°_{vap, bulk}, the heat of vaporization, is the total bonding energy of atoms in a bulk crystal. For silver, ΔH°_{fusion, bulk} = 11.3 kJ/mol and ΔH°_{vap, bulk} = 250 kJ/mol. From this we can calculate the heat of fusion of a 2 nm Ag nanocrystal:

ΔH°_fusion ≈ 11.3 - (0.025)(250) = 5.1 kJ/mol

The melting point of bulk silver is 962 °C = 1235 K. Assuming that the entropy of fusion is the same in the bulk and in the nanocrystal, the melting point of the nanocrystal should be 1235 K x (5.1/11.3) = 557 K = 284 °C, a drop of almost 700 degrees from the bulk value. Experimentally, the melting point of a 2 nm diameter silver nanocrystal drops about 800 degrees below that of the bulk, to 127 °C. This is a whopping big change in the melting point, which is in reasonable agreement with our rough estimate.

The same effect - energetic destabilization of the surface atoms relative to bulk atoms - results in the lower boiling point, higher vapor pressure, higher solubility, and higher reactivity of nanocrystals relative to microcrystals (or larger crystals) of the same material.

  11.5 Nanoscale metal particles

Five-fold twinning in a gold nanoparticle

Nanoscale metal particles have been the subject of intense research over the past 20 years, especially because of their unusual optical, magnetic, and catalytic properties. The synthesis of metal nanocrystals in various shapes has become increasingly sophisticated and rational, like the synthesis of semiconductor nanocrystals described above. By controlling the separate phases of nucleation and growth, and by using ligands that cap specific crystal faces during growth, it is possible to make metal nanocrystals of uniform size in a variety of interesting and useful shapes including cubes, truncated cubes, octahedra, triangular prisms, and high aspect ratio rods. By exploiting displacement reactions that replace one metal with another, complex hollow shapes such as nanocages (as shown at the left) can be made starting with other shapes. In this case, solid silver nanocubes are transformed to gold nanocages.

The Lycurgus cup (4th century Roman glass) derives its unique coloration from noble metal nanoparticles. The cup is red in transmitted light and green in scattered (reflected) light.

The interesting optical properties of nanocrystalline Au, Ag, Cu, and a number of other metals, derive from the collective oscillation of their valence electrons, a phenomenon known as plasmon resonance. Remember that in these metals, the electron mean free path is long (about 100 times larger than the size of the atoms), so the valence electrons feel only the average positive charge of the atomic cores as they zoom around the crystal. Light impinging on the metal acts as an oscillating electric field, pushing and pulling on the valence electrons at the characteristic frequency of the light wave. The situation is very much like a pendulum or a weight on a spring. The electrons, pushed away from their equilibrium positions, feel a restoring force that is proportional to their displacement. Their motion can be described by Hooke's Law:

F = kx

where the spring constant k determines the "stiffness" of the spring. In the case of the plasmon resonance, k is proportional to the number density of valence electrons n, and the square of the electronic charge e:

k = ne²/ε₀

The resonant frequency of the plasma oscillation is given by:

ω_p = (k/m)^1/2 = (ne²/m_eε₀)^1/2

where m_e is the electron mass. For most metals, the plasmon resonance is in the ultraviolet part of the spectrum, but for a few metals like Au, Ag, and Cu it is in the visible.

The colors of plasmonic gold nanoparticles depend on their size and shape.

For metal particles that are much smaller than the wavelength of light, this effect is called the localized surface plasmon resonance, or LSPR. There are three important consequences of the LSPR effect:

• The local electric field of the incoming light wave is greatly enhanced at the particle surface. This gives rise to huge enhancement factors in optical processes such as Raman scattering and fluorescence. Thus, certain analytical spectroscopic techniques are greatly enhanced by LSPR.
• Near the plasmon resonance frequency, metal nanocrystals absorb and scatter light very strongly. This makes them brightly reflective, and the strong light absorption can be exploited for light-induced local heating. These properties are being applied in medical diagnostics and therapy, e.g., for detection and photothermal destruction of cancer cells. By adjusting the size and shape of the gold nanoparticles, which are more stable than Ag and Cu in biological media, the plasmon frequency can be tuned to the tissue-transparent near-IR region of the spectrum between 700 and 900 nm. Small quantities of plasmonic Ag and Au particles also make brightly colored and strongly scattering pigments, e.g. in stained glass as shown above at the right.
• The plasmon frequency is sensitive to the refractive index of the particle's surroundings, i.e., its chemical environment. This makes metal nanoparticles of special interest for sensing and biosensing applications.

Theory of light scattering and absorption by metal nanoparticles. The valence electrons in metal nanoparticles oscillate in the electric field of a light wave. While the nature of these oscillations is somewhat complex in metal particles that are non-spherical, the theory for spherical particles is relatively simple and in fact was worked out over 100 years ago by German physicist Gustav Mie.

Mie considered the interaction of a spherical particle with a uniform electric field, E, oscillating at angular frequency ω (= 2π f). This is a good approximation when the particle diameter is much smaller than the wavelength of light, as shown on the left. The particle is embedded in a uniform, insulating material (e.g. a solvent) that has a dielectric constant ε_diel. For insulators, ε_diel is a positive real number.

The dielectric constant ε of a metal is actually a complex number:

$\epsilon =\epsilon '+i\epsilon ''$

Here the real part, ε', is related to the refraction of light, and the imaginary part, ε", is related to light absorption. Both ε' and ε" are dependent on the frequency of the light. For metals near the plasmon resonance frequency, ε' is typically a negative number.

The cross-section for absorption of the light wave by the particle is:

${\sigma _{absorption}}={\frac {9\omega }{c}}\epsilon _{diel}^{3/2}V{\frac {\epsilon _{metal}''}{(\epsilon _{metal}'+2\epsilon _{diel})^{2}+(\epsilon _{metal}'')^{2}}}$

and the cross-section for scattering is:

${\sigma _{scattering}}={\frac {3}{2\pi }}({\frac {\omega ^{4}}{c}})\epsilon _{diel}^{2}V^{2}{\frac {(\epsilon _{metal}'-\epsilon _{diel})^{2}+(\epsilon _{metal}'')^{2}}{(\epsilon _{metal}'+2\epsilon _{diel})^{2}+(\epsilon _{metal}'')^{2}}}$

The sum of these two is the cross-section for extinction:

${\sigma _{extinction}}={\sigma _{absorption}}+{\sigma _{scattering}}$

These cross-sections become large when the (ε'_metal + 2ε_diel) term in the denominator becomes small. This occurs when

$\epsilon _{metal}'\simeq -2\epsilon _{diel}$

For 15 nm diameter gold nanoparticles in water, this happens at about 580 nm, resulting in the characteristic wine-red color of colloidal gold solutions. Changing the solution environment (e.g., by adsorbing a molecule onto the gold surface) changes ε_diel and thus alters the color slightly.

It is important to note that the cross-section for scattering is proportional to the square of the volume of the particle, V², whereas the absorption is proportional to V. This means that very small gold particles (< 5 nm) are strongly absorbing but not strongly scattering. Larger particles (>30 nm) scatter light very strongly. Depending on the application, therefore, we choose larger or smaller particles.

One of the key complementary properties of noble metal nanoparticles that is important to their use in biomedicine is the ease with which they can be covalently conjugated with polymers or small molecules, typically via thiol or amine bonds at their surface. This imparts biological recognition properties to the particles that enables them to bind to specific biomolecular targets. The figure at the left illustrates some of the functionality that can be imparted to nanoparticles through surface functionalization.

Aggregation of Au nanoparticles (in this case by adding salt to a colloidal solution) causes a color change from wine red (left) to blue (right). Photo credit: George Lisensky, Beloit College

Functionalization of gold nanoparticles with thiol-terminated single-stranded DNA was the basis of one of the first nanoparticle sensors, developed by the Mirkin group at Northwestern University. DNA-coated nanoparticles have the characterstic wine-red plasmonic color of spherical nano-gold. However, when these particles are linked together by a complementary DNA strand, the resonance frequency shifs, resulting in a blue color. This color change, illustrated in the figure at the right, provides a "litmus test" for the presence of the target DNA sequence. "Melting" of the DNA - heating it to the temperature at which double stranded DNA dissociates to make single strands - reverses the color change. The DNA hybridization/melting transition is highly cooperative because of the aggregation of many gold particles, so the transition temperature is very sharp. With proper temperature control, the color change can be sensitive to a single base mismatch in the target DNA that is detected by this method.

General schematic of nanoflare-based detection.

Subsequent research has developed sophisticated diagnostic and therapeutic ("theranostic") applications for these spherical nucleic acid particles. These particles easily penetrate cell membranes and can report on the chemistry happening inside living cells.

An important property of gold nanoparticles in these applications is their ability to quench the fluorescence of reporter molecules that are near their surface. Nucleic acid strands that contain a hairpin loop can position fluorescent molecules near the gold surface, where their fluorescence is turned off by nanoparticle quenching. Hybridization of these sequences to target RNA or DNA causes the fluorescence to turn on by moving the fluorescent molecule away from the nanoparticle surface. These so called "nanoflares" can thus signal the up- or down-regulation of specific genes inside cells. Nanoflares are the basis of the Verigene System, developed and commercialized by Nanosphere, Inc. to detect markers for infectious diseases and cancers.

  11.6 Applications of Nanomaterials

PowerPoint slides for this section

  11.7 Discussion questions

• Explain how separating the nucleation and growth steps leads to nanoparticles of uniform size.
• A recent paper by Delia Milliron and coworkers (Nature, 2013, 500, 323–326, doi:10.1038/nature12398) describes plasmonic indium-tin-oxide (ITO) nanoparticles that can control the infrared transparency of windows. Explain how the plasmon resonance wavelength of the nanoparticles can be tuned by electrochemical doping, and how the invention could save some of the energy used to heat and cool buildings.

  11.8 Problems

1. Consider a spherical gold nanoparticle that contains 500 atoms. If the diameter of an atom is approximately 3 Å, what fraction of the gold atoms in the particle are on the surface?

2. Now consider small droplets of mercury that contains 500 atoms. Mercury atoms are also about 3 Å in diameter. The heat of vaporization of bulk mercury is 64.0 kJ/mol, and the vapor pressure of mercury is 0.00185 torr = 2.43 x 10^-6 atm. The surface tension of mercury (γ_Hg) is 0.518 N/m, and the surface excess energy can be calculated as γ_HgA, where A is the surface area. Using this information and the Clausius-Clapyron equation (P = const•exp(-ΔH_vap/RT)), calculate the vapor pressure of these small droplets of mercury.

3. James Heath and coworkers (Phys. Rev. Lett. 1995, 75, 3466) have observed Ostwald ripening in thin films of gold nanoparticles at room temperature. Starting with an uneven distribution of particle sizes, they find that the large particles grow at the expense of smaller ones. Can you explain this observation, based on your answers to problems (1) and (2)?

4. The bandgap of bulk germanium is 0.67 eV. What bandgap would you expect for a 4 nm diameter Ge nanocrystal? Use the Brus formula,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/en.wikibooks.org/v1/":): {\displaystyle \Delta {{E}_{gap}}\approx \frac{{{h}^{2}}}{8\mu {{R}^{2}}}-\frac{{1.8{e}^{2}}}{4R\pi \varepsilon {{\varepsilon }_{0}}}+...}

where R is the particle radius, ε_Ge = 16.2, h = 6.6 10^-34 J s, 1 eV = 1.6 10^-19 J, 1 J = 1 kg m²/s². and e²/4πε₀ = 1.44 10^-9 eV m. Assume that the electron-hole reduced mass μ is approximately 40% of the free electron mass, m_e = 9.1 10^-31 kg.

5. Grecian Formula (a hair coloring product) until recently contained lead acetate, which reacts with the cysteine in hair to make PbS. In bulk form, PbS is a semiconductor with a band gap of 0.3 eV (1 eV = 1240 nm). The particles are initially very small but grow as more Grecian Formula is applied and reacts with cysteine. As the particles grow, they change progressively from colorless to yellow to black. Explain why the particles are initially colorless and why their color changes. (Grecian formula now uses Bi, which is less toxic than Pb, and works by the same mechanism)