HSC Extension 1 and 2 Mathematics/3-Unit/Preliminary/Parametrics
The parametric form of a curve is an algebraic representation which expresses the co-ordinates of each point on the curve as a function of an introduced parameter, most frequently . This contrasts with Cartesian form in that parametric equations do not describe an explicit relation between and . This relation must be derived in order to convert from parametric to Cartesian form.
In 3-unit, parametrics focuses on a parametric representation of the quadratic, moving from parametric to Cartesian form and vice-versa, and manipulating geometrical aspects of the quadratic with parametrics. Recognition of other parametric forms is also useful, and more forms are introduced and dealt with in the 4-unit topic, conics.
Reasons for using the parametric form[edit | edit source]
In specific situations (in the school syllabus, primarily Conic sections), the parametric representation can be useful because:
- points on the curve are represented by a single number, not two, simplifying algebra;
- some elegant results are possible; for instance, in the standard paramaterisation of the quadratic, the gradient is equal to the parameter, ;
- some curves, which cannot be expressed in functional form (for example, the circle, which is neither a function of nor of ) can be conveniently expressed in parametric form;
- intuitively, it allows for an easier way to find points on the graph: you can sub in any value for the parameter and instantly find a point, whereas a relational form is not deterministic in the same way.
Furthermore, the parametric form occurs in certain natural phenomena. For instance, using the equations of motion, a thrown ball's location at any time can be calculated using the laws of projectile motion. This is implicitly paramaterising the ball's path by time; to find the shape of the ball's path, (which we know is a parabola) we must use parametrics, to eliminate time, , from the equations.
Converting parametric to Cartesian forms[edit | edit source]
One of the simplest parametric forms is the line:
By inspection, it is obvious that this describes the line . However, what is the formalised approach for doing this?
We are looking for some relation between and which has no in it. In other words, we want to eliminate from the equations. In the above example, we did this by equating the first and second equations, eliminating .
Another example:[edit | edit source]
We solve equation 1 for t, and substitute into equation 2:
Sub into equation 2:
Here we have a Cartesian form, as required.
Three standard parametric forms[edit | edit source]
These parametric forms occur frequently, and should be recognised by 3- and 4-unit students.
Parabola[edit | edit source]
The standard paramaterisation of the parabola describes one with focal length and with its vertex at the origin. In Cartesian form, this is given as
In parametric form, this is given as
Eliminating allows us to verify that this is equivalent to the Cartesian form:
as required.
Circle[edit | edit source]

The circle with radius and center at the origin can be written in Cartesian form as
Introducing the parameter, , this is:
We convert to Cartesian as follows:
Recalling the trig identity,
we conclude
as required.
Geometrical interpretation[edit | edit source]
Unlike most parametrics, the conic sections are paramaterised by instead of . For the circle, this implies a geometric representation: represents the angle the point makes with the axis.
Ellipse[edit | edit source]
Conceptually, an ellipse is just a 'squished' circle. The parametric form makes this clear:
The cos and sin are still there, but they are now multiplied by different constants so that the and components are stretched differently. We can turn this into the parametric form in a similar fashion to the circle:
which is the standard form of an ellipse, with and intercepts at and , respectively.
Properties of the parabola[edit | edit source]
3-Unit students are expected to remember the parametric description of a parabola (). They are also expected to know (and/or be able to quickly derive) the equations of the tangent and the normal to the parabola at the point and at the point .
Derivation of equations of the tangent and the normal[edit | edit source]
Differentiating each parametric equation with respect to ,
Then the gradient can be obtained by dividing by (this is the chain rule):
Note that this result could have been derived without the chain rule, by taking the derivative of the Cartesian form (with respect to ) and solving for . However, the above derivation is faster and more elegant.
The equation of the tangent at P[edit | edit source]

The gradient of the tangent at a point then is . The equation of the tangent at is:
- Using the point-gradient formula , the equation is:
The equation of the normal at P[edit | edit source]
The gradient of the normal at the point is (since two perpendicular lines with gradients and must have ). Similarly to the derivation of the equation of the tangent:
Chords of a parabola[edit | edit source]
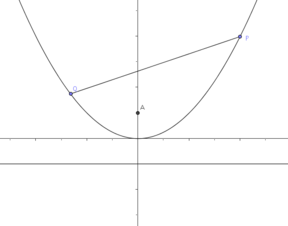
Suppose that and are two distinct points on the parabola . We can derive the equation for the line by finding the gradient and using the point-gradient formula:
so the chord is
Intersection of tangents[edit | edit source]
The points and lie on the parabola . The intersection of the tangents at and can be found in terms of and :
- The tangents are:
- Subtracting these,
- Substituting into the original tangent formula,
So the point of intersection is described by .




















































