Graph Theory/Definitions
Graph, node and edge[edit | edit source]

A graph is an ordered pair where,
- V is the vertex set whose elements are the vertices, or nodes of the graph. This set is often denoted or just .
- E is the edge set whose elements are the edges, or connections between vertices, of the graph. This set is often denoted or just . If the graph is undirected, individual edges are unordered pairs where and are vertices in . If the graph is directed, edges are ordered pairs .
Two graphs and are considered equal when and .
The order of a graph is the number of vertices in it, usually denoted or or sometimes . The size of a graph is the number of edges in it, denoted or , or sometimes . If and , the graph is called empty or null. If and , the graph is considered trivial. If and , the graph is called discrete.
Undirected graph[edit | edit source]
An undirected graph is one in which edges have no orientation. The edge (a, b) is identical to the edge (b, a), i.e., they are not ordered pairs, but sets {u, v} (or 2-multisets) of vertices.
Directed graph[edit | edit source]
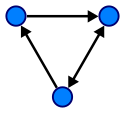
A directed graph or digraph is an ordered pair D = (V, A) with
- V a set whose elements are called vertices or nodes, and
- A a set of ordered pairs of vertices, called arcs, directed edges, or arrows.
An arc a = (x, y) is considered to be directed from x to y; y is called the head and x is called the tail of the arc; y is said to be a direct successor of x, and x is said to be a direct predecessor of y. If a path leads from x to y, then y is said to be a successor of x and reachable from x, and x is said to be a predecessor of y. The arc (y, x) is called the arc (x, y) inverted.
A directed graph D is called symmetric if, for every arc in D, the corresponding inverted arc also belongs to D. A symmetric loop-less directed graph D = (V, A) is equivalent to a simple undirected graph G = (V, E), where the pairs of inverse arcs in A correspond 1-to-1 with the edges in E; thus the edges in G number |E| = |A|/2, or half the number of arcs in D.
A variation on this definition is the oriented graph, in which not more than one of (x, y) and (y, x) may be arcs.
Example[edit | edit source]

In the image you can see a graph.
The set of the vertices of the graph is .
The set of edges of the graph is .
The order of this graph is .
The size of this graph is .
Subgraphs, contractions, and graph minors[edit | edit source]
Subgraphs[edit | edit source]
Given a graph and a graph , is a subgraph of if and only if and . A clear result of this is that the every graph has as subgraphs at least the empty graph and itself, as the empty graph has as its vertex and edge set the empty set, both of which are subsets of every set, and and . Additionally, every subgraph of some graph can be formed from by a sequence of edge deletions and vertex deletions. Formally, there exists a sequence with and , and for each , it is the case that is either formed from by a single edge removal or a single vertex removal.
Edge contraction[edit | edit source]
Given a graph , and some edge between vertices in , the graph formed by contracting the edge is the graph with vertex set equal to , where is the vertex formed by the contraction of , and is adjacent to all neighbours of and all neighbours of .
Graph minors[edit | edit source]
Given a graph , and another graph , is called a if is formed from by the insertion of vertices of degree two into the edges of . This process is called subdivision, and the vertices of are known as branch vertices of , while the other vertices in are called subdividing vertices. Now, if some graph contains a as a subgraph, then is said to have as a topological minor.
Given a graph , and another graph , is called an if is formed from by replacing the vertices of with connected graphs such that if a vertex is replaced by a connected graph , there are edges connecting to each of the graphs replacing the vertices that are adjacent to in , and only to those graphs. This process is called inflation, hence the use of an to represent it, and the graphs that replace vertices in are known as the branch sets of . Now, if some graph contains an as a subgraph, then is said to have as a minor, which is denoted as .
Theorem: If is a topological minor of , then .
Proof: Since is a topological minor of , there is some a subgraph of . Call that . Number the branch vertices of from to . Now, for each subdividing vertex in , add to the branch set containing the branch vertex at minimal distance from . If has two branch vertices at minimal distance, add it to the branch set containing the branch vertex with lower number. Now, every vertex is in a branch set, and the branch sets are disjoint, and each is connected. This yields an that is a subgraph of , and therefore, .
Incidence, adjacence, degree[edit | edit source]
The concept of incidence associates an edge to the nodes that are connected by that edge. For example the edge is incident to the nodes and .
If there is an edge that connects two nodes, we say that those nodes are adjacent. More formally, are adjacent if . The neighbourhood of a node v, denoted , is the set of all the nodes that are adjacent to it.
The degree of a node v, denoted , is the number of edges incident to it. In a directed graph, the in-degree and out-degree count the number of directed edges coming into and out of a vertex respectively.
The minimum degree of a graph , denoted , is , the minimum across the vertices of of the degrees of those vertices.
Similarly, the maximum degree of a graph , denoted , is , the maximum across the vertices of of the degrees of those vertices.
Handshaking lemma[edit | edit source]
The handshaking lemma is a consequence of the degree sum formula (also sometimes called the handshaking lemma),
Proof Euler's proof of the degree sum formula uses the technique of double counting: he counts the number of incident pairs where e is an edge and vertex v is one of its endpoints, in two different ways. Vertex v belongs to deg(v) pairs, where deg(v) (the degree of v) is the number of edges incident to it. Therefore the number of incident pairs is the sum of the degrees. However, each edge in the graph belongs to exactly two incident pairs, one for each of its endpoints; therefore, the number of incident pairs is 2|E|. Since these two formulas count the same set of objects, they must have equal values.
In a sum of integers, the parity of the sum is not affected by the even terms in the sum; the overall sum is even when there is an even number of odd terms, and odd when there is an odd number of odd terms. Since one side of the degree sum formula is the even number 2|E|, the sum on the other side must have an even number of odd terms; that is, there must be an even number of odd-degree vertices.
Mantel's theorem[edit | edit source]
The maximum number of edges in an n-vertex triangle-free graph is
Proof:
Suppose that is a graph on vertices. We will find how many edges this graph can have.
For every edge , if there was a vertex adjacent to and to , we would have a triangle. So we know that such vertex does not exist and that the neighbourhood of is disjoint to the neighbourhood of :
This means that any other vertex can be either adjacent to or adjacent to . When we count degrees of and , we see that their sum is at most , because a vertex can be counted either as neighbour of either as neighbour of :
The inequality above is valid for every edge. So we have as many inequalities as many edges. If we sum all these inequalities we see that the degree of a vertex will be there times, so we have to sum . The inequality becomes:
Since each edge has two end vertices, the sum of the degrees is exactly twice the number of edges:
In with the standard inner product, the Cauchy–Schwarz inequality is:
The two formulas above imply:
Solving for we get:
Traversals[edit | edit source]
When examining a graph, quite often we will need to know the various ways to get from one vertex to another, and the different types of traversals this can take. To understand the concept of traversals, we can imagine that the nodes of the graph are squares inside a city, and the edges are the lanes connecting them. Imagine that you have to go by foot from one square to another, and there are some intermediate squares between you and your destination. It is possible to write down the list of all lanes that you have to walk through, the concept of walk is a formalization of that intuitive concept.
Walk, closed walk, circuit and cycle[edit | edit source]
- A u-v walk is defined as a sequence of vertices starting at u and ending at v, where consecutive vertices in the sequence are adjacent vertices in the graph

A drawing of a labelled graph on 6 vertices and 7 edges. - A closed walk is a walk in which the first and last vertices are the same
- A u-v trail is a u-v walk, where no edge is repeated (each edge is used at most once)
- A circuit or closed trail is a trail in which the first and last vertices are the same
- A u-v path is a u-v walk, where no vertex is repeated (each vertex is used at most once)
- A cycle is a closed path in which the first and last vertices are the same
For example, in the image to the right, is a walk. While , and are cycles.
Distance in a Graph[edit | edit source]
Now, we need to define a concept of distance in a graph; this helps us encode more data in the graph.
- Length of a walk
- the number of edges used in a particular walk.
If an edge is used more than once, then it is counted more than once.
A trivial walk is one where the length is 0.
Theorem[edit | edit source]
If a graph G contains a u-v walk of length , then G contains a u-v path of length ≤.
Proof:
- Let P be a u-v walk of shortest length. We claim that P is a path (since being the shortest, it eliminates repeated vertices).
- Suppose not. Suppose that P is not a path. Then, at least one vertex is repeated (used twice). Then, set , where is the length of P.
- And, we know that for some .
- Then, remove the repeated vertex(ices) to get . But, then we get that the length of P' is smaller than the length of P, which contradicts our assumption that P was the walk of shortest length.
- So, P must be a path, and it is shorter than any other walk that has vertices in P.
- Thus, there is a u-v path of length at most .
Graph Distance[edit | edit source]
The graph distance between two vertices and of a finite graph is the minimum length of the paths connecting them. The length of a graph geodesic, too.
A geodesic is a shortest path between two graph vertices of a graph.
If no such path exists ( if the vertices lie in different connected components ), then the distance is set equal to .
Geodesics[edit | edit source]
For any two vertices u and v in a graph G, the distance between u and v is defined to be the length of the shortest path between u and v, denoted d(u,v).
A path of length d(u,v) is called a geodesic.
Properties of d(u,v):
For a geodesic P:u=u0u1u2...uk=v and some 0≤i,j≤k:
- d(u0uk) = k
- d(uiui) = 0 (not travelling anywhere)
- d(u0ui) = i
- d(uiuj) = |j-i|
More Graph Parameters[edit | edit source]
Using d(u,v), we can find other parameters of the graph G:
- Diameter: the diameter diam(G) is the largest distance d(u,v) between any two vertices of a connected graph; i.e. diameter is the max{d(u,v)} for all sets of u,v in V(G).
- Graph Eccentricity
The eccentricity of a graph vertex in a connected graph is the maximum graph distance between and any other vertex of .
For a disconnected graph, all vertices are defined to have infinite eccentricity.
- Graph Diameter : The maximum graph eccentricity
- Graph Radius : The minimum graph eccentricity
Connectivity[edit | edit source]
Whether or not it is possible to traverse a graph from one vertex to another is dependent on how connected a graph is.
Definition of Connectedness[edit | edit source]
- If there is a u-v path in G, then we say that u and v are connected
- If there is a u-v path for every pair of vertices u and v in G, then we say that G is connected
Theorems on Connectedness[edit | edit source]
Theorem: Let G be a graph of order at least 3. If there are distinct vertices u and v in G so that G-u and G-v are both connected, then G is also connected.
Proof: Let w be a G vertex, which is different from both u and v. We want to prove connectedness, i.e., that for every pair (x,y) of vertices in G, there is an x-y walk in G. We may consider three (partly overlapping) cases:
- If neither x nor y is u, then there is an x-y walk in G-u, and this also is an x-y walk in G.
- If neither x nor y is v, then there is an x-y walk in G-v, and this also is an x-y walk in G.
- If {x,y} = {u,v}, then employ the first two cases in order to see that there is a u-w walk and a w-v walk. Combining them indeed yields a u-v walk.
Vertex and Edge Connectivity[edit | edit source]
A graph G is called k-connected if for every , and , is connected, and .
Similarly, a graph G is called edge-connected if for every , and , is connected, and .
The connectivity of G is the greatest k such that G is k-connected, and is denoted by .
Relatedly, the edge-connectivity of G is the greatest such that G is edge-connected, and is denoted by .
Theorems on Connectivity[edit | edit source]
Theorem: Let G be a k-connected graph. Then, , G is i-connected.
Proof: Since G is k-connected, for all , is connected. Then, since , for all , is also connected.
Theorem: Let G be a nontrivial graph. Then, .
Proof: Take v a vertex of degree in G. Then, removing all edges in G that are incident with v disconnects v from the rest of the graph, provided that . Therefore, G cannot be edge-connected, and so .
|
Exercise: Connectivity
|
Isomorphism[edit | edit source]
An isomorphism of graphs G and H is a bijection between the vertex sets of G and H
such that any two vertices u and v of G are adjacent in G if and only if ƒ(u) and ƒ(v) are adjacent in H. This kind of bijection is commonly called "edge-preserving bijection", in accordance with the general notion of isomorphism being a structure-preserving bijection.
In the above definition, graphs are understood to be undirected non-labeled non-weighted graphs. However, the notion of isomorphism may be applied to all other variants of the notion of graph, by adding the requirements to preserve the corresponding additional elements of structure: arc directions, edge weights, etc., with the following exception. When spoken about graph labeling with unique labels, commonly taken from the integer range 1,...,n, where n is the number of the vertices of the graph, two labeled graphs are said to be isomorphic if the corresponding underlying unlabeled graphs are isomorphic.
If an isomorphism exists between two graphs, then the graphs are called isomorphic and we write . In the case when the bijection is a mapping of a graph onto itself, i.e., when G and H are one and the same graph, the bijection is called an automorphism of G.
The graph isomorphism is an equivalence relation on graphs and as such it partitions the class of all graphs into equivalence class es. A set of graphs isomorphic to each other is called an isomorphism class of graphs.
Example[edit | edit source]
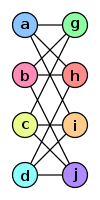
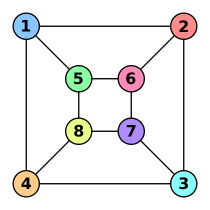
The two graphs shown below are isomorphic, despite their different looking drawings.
| Graph G | Graph H | An isomorphism between G and H |
|---|---|---|
|
|
ƒ(a) = 1
ƒ(b) = 6 ƒ(c) = 8 ƒ(d) = 3 ƒ(g) = 5 ƒ(h) = 2 ƒ(i) = 4 ƒ(j) = 7 |
Motivation[edit | edit source]
The formal notion of "isomorphism", e.g., of "graph isomorphism", captures the informal notion that some objects have "the same structure" if one ignores individual distinctions of "atomic" components of objects in question, see the example above. Whenever individuality of "atomic" components (vertices and edges, for graphs) is important for correct representation of whatever is modeled by graphs, the model is refined by imposing additional restrictions on the structure, and other mathematical objects are used: digraphs, labeled graphs, colored graphs, rooted trees and so on. The isomorphism relation may also be defined for all these generalizations of graphs: the isomorphism bijection must preserve the elements of structure which define the object type in question: arcs, labels, vertex/edge colors, the root of the rooted tree, etc.
The notion of "graph isomorphism" allows us to distinguish graph properties inherent to the structures of graphs themselves from properties associated with graph representations: graph drawings, data structures for graphs, graph labelings, etc. For example, if a graph has exactly one cycle, then all graphs in its isomorphism class also have exactly one cycle. On the other hand, in the common case when the vertices of a graph are (represented by) the integers 1, 2,... N, then the expression
may be different for two isomorphic graphs.
Complement[edit | edit source]

The complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and removes all the edges that were previously there. It is not, however, the set complement of the graph; only the edges are complemented.
Formal construction[edit | edit source]
The complement of a graph is a graph such that for all pairs of vertices , there is an edge if and only if . If we let , we see that .
Applications and examples[edit | edit source]
Several graph-theoretic concepts are related to each other via complement graphs:
- The complement of an edgeless graph is a complete graph and vice versa.
- The complement of any triangle-free graph is a claw-free graph.
- A self-complementary graph is a graph that is isomorphic to its own complement.
- Cographs are defined as the graphs that can be built up from disjoint union and complementation operations, and form a self-complementary family of graphs: the complement of any cograph is another (possibly different) cograph.
Tree[edit | edit source]
A tree is a type of connected graph. An directed graph is a tree if it is connected and has no cycles. An undirected graph is considered a tree if it is connected, has edges and is acyclic (a graph that satisfies any two of these properties satisfies all three).
|
Exercise: Equivalent Definitions Show that the following are equivalent definitions for a tree:
Hint: To keep the total proof short, put the definitions in a suitable order, and then prove A=>B=>C=>D=>E=>A. Take particular care over graphs with zero and one node. |
Rooted tree[edit | edit source]
A tree is called a rooted tree if one vertex has been designated the root, in which case the edges have a natural orientation, towards or away from the root. The tree-order is the partial ordering on the vertices of a tree with u ≤ v if and only if the unique path from the root to v passes through u. A rooted tree which is a subgraph of some graph G is a normal tree if the ends of every edge in G are comparable in this tree-order whenever those ends are vertices of the tree.
In a rooted tree, the parent of a vertex is the vertex connected to it on the path to the root; every vertex except the root has a unique parent. A child of a vertex v is a vertex of which v is the parent.
In a rooted tree and all vertices have at most one parent.
Complete graph[edit | edit source]
A complete graph is one for which all pairs of vertices are connected by an edge. A complete graph on vertices is denoted .
Any graph that has a subgraph isomorphic to is non-planar.
|
Exercise: Planarity
|
|
Exercise: Subgraphs and Isomorphisms
|
Bipartite graph[edit | edit source]
A graph is bipartite if the vertex set can be partitioned into two disjoint subsets such that for every edge , and are in opposite subsets.
Additionally, a graph is bipartite if and only if it contains no odd cycles.
Proof:
- Let be an arbitrary and fixed graph with an odd cycle.
is bipartite contains no odd cycles
- Assume for the sake of contradiction that contains an odd cycle.
- Let be two disjoint subsets that form a bipartition on .
- Choose an odd cycle in and, without loss of generality, choose some node from . Traverse starting from , noting that each node is in the different subset from its neighbors by definition of a bipartite graph.
- The last node in this traversal, , must be in , as is an odd cycle. However, is adjacent to by definition of a cycle, which is a contradiction as contains two adjacent nodes, so cannot contain an odd cycle.
- As we have looked at an arbitrary and chose without loss of generality from , we have proven the implication.
contains no odd cycles is bipartite
- We present an algorithm to sort the nodes into two disjoint sets.
- Fix an arbitrary node .
- For each node in the graph, calculate the shortest path from to .
- Let be the sets of nodes such that the shortest path from to are even and odd respectively.
- We look without loss of generality at to prove this algorithm's correctness.
- Assume for the sake of contradiction two nodes are adjacent. Let represent the shortest paths from to respectively.
- If and do not intersect, forms a cycle of odd length as and trivially have the same parity, which is a contradiction.
- If and intersect, we choose the intersection closest to . Note cannot be either or , as the shortest paths from to would not have the same parity. Observe that the distance from to and must be the same length, otherwise the shortest path to either would travel through the other node. However, this is a contradiction as would be an odd cycle.
- Therefore, no two nodes in can be adjacent, and as we looked at without loss of generality, we have proven the algorithm correct and therefore the reverse implication.
Complete Bipartite Graph[edit | edit source]
The complete bipartite graph is the graph composed of two disjoint subsets of cardinality respectively, such that contains an edge between each node in and every node in .










































































































































