Geometry/Appendix C
A[edit | edit source]
Acute Angle[edit | edit source]
- See Angle
Algebraic Properties of Equality[edit | edit source]
For real numbers a, b, and c
Addition Property of Equality: if a=b , then a+c=b+c
Subtraction Property of Equality: if a=b , then a-c+=b-c
Multiplication Property of Equality: is a=b, then ac=bc
Division Property of Equality: if a=b and c≠0 , then (a/c)=(b/c)
Symmetric Property of Equality: if a=b, then b=a
Transitive Property of Equality: if a=b and b=c , then a=c
Reflexive Property of Equality: if a=a , then a=a
Substitution Property of Equality: if a=b, then a can be substituted for b
Distributive Property of Equality: a(b+c)=ab+ac
Angle[edit | edit source]

A figure is an angle if and only if it is composed of two rays which share a common endpoint. Each of these rays (or segments, as the case may be) is known as a side of the angle (For example, in the illustration at right), and the common point is known as the angle's vertex (point B in the illustration). Angles are measured by the difference of their slopes. The units for angle measure are radians and degrees. Angles may be classified by their degree measure.
- Acute Angle: an angle is an acute angle if and only if it has a measure of less than 90°
- Right Angle: an angle is an right angle if and only if it has a measure of exactly 90°
- Obtuse Angle: an angle is an obtuse angle if and only if it has a measure of greater than 90°
- Straight Angle: an angle is a straight angle if and only if it has a measure of exactly 180°
Using the Right Angle Congruence Theorem and the Straight Angle Congruence Theorem, all right angles and all straight angles are congruent
Angle Addition Postulate[edit | edit source]
If P is in the interior of an angle , then
Arithmetic mean[edit | edit source]
The arithmetic mean of 2 numbers a and b can be calculated as: arithmetic mean=(a+b)/2
B[edit | edit source]
Bisector[edit | edit source]
A figure bisects another figure if and only if it splits the figure it intersects into two equal parts
C[edit | edit source]
Center of a circle[edit | edit source]
Point P is the center of circle C if and only if all points in circle C are equidistant from point P and point P is contained in the same plane as circle C.
Circle[edit | edit source]
The set of all points in a plane that are equidistant from a given point (called the center of the circle).
Circumference[edit | edit source]
The distance around a circle.
It is calculated as:
C=2πr (where r is the radius of the circle)
Complementary Angles[edit | edit source]
Two angles are complimentary if and only if the sum of their measures equals up to 90 degrees.
Concave[edit | edit source]
A polygon is said to be concave if and only if it contains at least one interior angle with a measure greater than 180° exclusively and less than 360° exclusively.
Congruency[edit | edit source]
Two figures are congruent if and only if they have the same measure. It is designated by "≅".
Corresponding angles[edit | edit source]
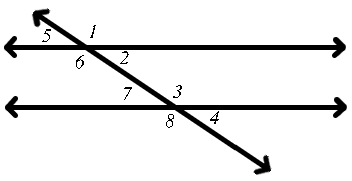
Two angles formed by a transversal intersecting with two lines are corresponding angles if and only if one is on the inside of the two lines, the other is on the outside of the two lines, and both are on the same side of the transversal.
Corresponding Angles Postulate[edit | edit source]
If two lines cut by a transversal are parallel, then their corresponding angles are congruent.
Corresponding Parts of Congruent Triangles are Congruent Postulate[edit | edit source]
The Corresponding Parts of Congruent Triangles are Congruent Postulate (CPCTC) states:
- If ∆ABC ≅ ∆XYZ, then all parts of ∆ABC are congruent to their corresponding parts in ∆XYZ. For example:
- ≅
- ≅
- ≅
- ∠ABC ≅ ∠XYZ
- ∠BCA ≅ ∠YZX
- ∠CAB ≅ ∠ZXY
CPCTC also applies to all other parts of the triangles, such as a triangle's altitude, median, circumcenter, et al.
Cosine[edit | edit source]
A trigonometric ratio, abbreviated as cos.
cos(θ)=adjacent/hypotenuse
D[edit | edit source]
Diameter[edit | edit source]
A line segment is the diameter of a circle if and only if it is a chord of the circle which contains the circle's center.
- See Circle
Distance[edit | edit source]
Distance between 2 points can be calculated as the absolute value of the difference of the coordinates of the points.
In a coordinate plane, distance for points A(x1,y1) and B(x2,y2) can be calculated as:
d(AB)=√((y2-y1)2+(x2-x1)2)
The distance between a point and a line is measured by the perpendicular segments connecting the 2 (using the Perpendicular postulate).
G[edit | edit source]
Geometric Mean[edit | edit source]
For 2 positive numbers a and b, the geometric mean of a and b is the positive number x that satisfies (a/x)=(x/b). So, x2=√(ab)
geometric mean of a and b = (a/x)=(x/b) : x2=√(ab)
H[edit | edit source]
Height of a paralellogram[edit | edit source]
The perpendicular distance bewtween 2 bases of a paralellogram
Hypotenuse[edit | edit source]
In a right triangle, the side opposite of the right angle.
Using the Pythagorean Theorem, the measure of the hypotenuse can be calculated as:
c2=a2=b2 (where c is the hypotenuse and a and b are legs of the right triangle)
L[edit | edit source]
Line[edit | edit source]
A collection of points is a line if and only if the collection of points is perfectly straight (aligned), is infinitely long, and is infinitely thin. Between any two points on a line, there exists an infinite number of points which are also contained by the line. Lines are usually written by two points in the line, such as line AB, or
Line segment[edit | edit source]

A collection of points is a line segment if and only if it is perfectly straight, is infinitely thin, and has a finite length. A line segment is measured by the shortest distance between the two extreme points on the line segment, known as endpoints. Between any two points on a line segment, there exists an infinite number of points which are also contained by the line segment.
I[edit | edit source]
Interior angle of a regular polygon[edit | edit source]
The interior angles of a regular polygon are all congruent. As such, the measure of one interior angle of a regular polygon with n number of sides can be calculated as:
int angle = ((n-2)180)/n
Isosceles Trapezoid[edit | edit source]
A trapezoid in which the legs are congruent.
Isosceles Triangle[edit | edit source]
A triangle with at least 2 congruent sides.
Using the Base Angles theorem, the angles opposite of the congruent sides are also congruent.
L[edit | edit source]
Linear pair[edit | edit source]
The adjacent angles whose noncommon sides are opposite rays.
Using the Linear Pair Postulate, the angles in a linear pair are also supplementary.
If 2 angles forming a linear pair are congruent, then both the angles are right angles and the lines containing the angles are perpendicular.
M[edit | edit source]
Major arc[edit | edit source]
An arc whose measure is greater than 180 degrees. It must be named by 3 points.
Midsegment of a Trapezoid[edit | edit source]
A segment that connects the midpoints of the legs of a trapezoid.
It is parallel to the bases and the length of it is the arithmetic mean of the measures of the bases.
Minor arc[edit | edit source]
An arc whose measure is less than 180 degrees.
P[edit | edit source]
Parallel lines[edit | edit source]
Two lines or line segments are said to be parallel if and only if the lines are contained by the same plane and have no points in common if continued infinitely.
In a coordinate plane, two lines are parallel if and only if they share the same slope.
Parallel planes[edit | edit source]
Two planes are said to be parallel if and only if the planes have no points in common when continued infinitely.
Perpendicular lines[edit | edit source]
Two lines that intersect at a 90° angle.
In a coordinate plane, two lines are perpendicular if and only if their slopes' products are equal to -1 (or if the slopes are negative reciprocals).
Perpendicular Postulate[edit | edit source]
Given a line, and a point P not in line , then there is one and only one line that goes through point P perpendicular to
Plane[edit | edit source]
An object is a plane if and only if it is a two-dimensional object which has no thickness or curvature and continues infinitely. A plane can be defined by three points. A plane may be considered to be analogous to a piece of paper[1].
Point[edit | edit source]
A point is a zero-dimensional mathematical object representing a location in one or more dimensions[2]. A point has no size; it has only location.
Polygon[edit | edit source]
A polygon is a closed plane figure composed of at least 3 straight lines. Each side has to intersect another side at their respective endpoints, and that the lines intersecting are not collinear.
R[edit | edit source]
Radius[edit | edit source]
The radius of a circle is the distance between any given point on the circle and the circle's center.
All radii in the same circle (or congruent circles) have the same measure.
- See Circle
Ray[edit | edit source]
A ray is a straight collection of points which continues infinitely in one direction. The point at which the ray stops is known as the ray's endpoint. Between any two points on a ray, there exists an infinite number of points which are also contained by the ray.
Regular Polygon[edit | edit source]
A regular polygon is a polygon that is equilateral and equiangular.
Ruler Postulate[edit | edit source]
The points on a line can be matched one to one with the real numbers. The real number that corresponds to a point is the point's coordinate. The distance between two points is the absolute value of the difference between the two coordinates of the two points.
S[edit | edit source]
Semicircle[edit | edit source]
An arc whose measure is 180 degrees.
Sum of the interior angles of a polygon[edit | edit source]
The sum of the interior angles of a polygon with n number of sides is calculated as:
sum int angles = (n-2)180
Supplementary Angles[edit | edit source]
Two angles are supplementary if and only if the sum of their measures equal up to 180 degrees.
- Geometry Main Page
- Motivation
- Introduction
- Geometry/Chapter 1 - HS Definitions and Reasoning (Introduction)
- Geometry/Chapter 1/Lesson 1 Introduction
- Geometry/Chapter 1/Lesson 2 Reasoning
- Geometry/Chapter 1/Lesson 3 Undefined Terms
- Geometry/Chapter 1/Lesson 4 Axioms/Postulates
- Geometry/Chapter 1/Lesson 5 Theorems
- Geometry/Chapter 1/Vocabulary Vocabulary
- Geometry/Chapter 2 Proofs
- Geometry/Chapter 3 Logical Arguments
- Geometry/Chapter 4 Congruence and Similarity
- Geometry/Chapter 5 Triangle: Congruence and Similiarity
- Geometry/Chapter 6 Triangle: Inequality Theorem
- Geometry/Chapter 7 Parallel Lines, Quadrilaterals, and Circles
- Geometry/Chapter 8 Perimeters, Areas, Volumes
- Geometry/Chapter 9 Prisms, Pyramids, Spheres
- Geometry/Chapter 10 Polygons
- Geometry/Chapter 11
- Geometry/Chapter 12 Angles: Interior and Exterior
- Geometry/Chapter 13 Angles: Complementary, Supplementary, Vertical
- Geometry/Chapter 14 Pythagorean Theorem: Proof
- Geometry/Chapter 15 Pythagorean Theorem: Distance and Triangles
- Geometry/Chapter 16 Constructions
- Geometry/Chapter 17 Coordinate Geometry
- Geometry/Chapter 18 Trigonometry
- Geometry/Chapter 19 Trigonometry: Solving Triangles
- Geometry/Chapter 20 Special Right Triangles
- Geometry/Chapter 21 Chords, Secants, Tangents, Inscribed Angles, Circumscribed Angles
- Geometry/Chapter 22 Rigid Motion
- Geometry/Appendix A Formulae
- Geometry/Appendix B Answers to problems
- Appendix C. Geometry/Postulates & Definitions
- Appendix D. Geometry/The SMSG Postulates for Euclidean Geometry









