Fractals/Mathematics/group/Binary adding machine
"Adding machines have played an important role in dynamical systems, and in the theory of groups acting on trees. "[1]
Structure[edit | edit source]
Alphabet is a set consisting of two symbols so it is called binary alphabet:
Word c is a sequence of symbols ( string). It can be dsiplayed in two ways :[2]
- a little-endian (least-significant-bit-first) :
- a big-endian :
When :
- is on the right side it is easier to treat it as a binary number
- is on the leftt side it is easier for machine
Space of words denote the set of all infinite strings over the alphabet.
The strings (, 0, 1, 00, 01, 10, 11, 000, etc.) would all be in this space.
represents the empty string
Action[edit | edit source]

Here is only one transformation ( action ) a ona a input word c :
where :
- is a lsb,[3] first symbol ( here at the beginning, but for binary notation it will be at the end of sequence)
- is a rest of the word
Transformation is defined by 2 recursion formulae :
- if the first symbol is zero then we change it to one and the rest of the word remains unchanged
- if it is one :
- we change it to zero
- carry 1 to next column.[4]
- aply action to the next column (symbol) until last column
Formally:
or in other notation :
"This transformation is known as the adding machine, or odometer, since it describes the process of adding one to a binary integer." [5]
More explicitly :[6]
if and only if
Both input and output are binary numbers least-significant bit first.
Examples[edit | edit source]
Word c is a sequence of n symbols ( from 0 to n-1) representing binary integer :
where is an element of binary alphabet X ={0,1}
without carry because lsb :
0 + 1 --- 1
Here lsb then c_0+1>1 so one has to carry 1 to next column
1 + 1 --- 10
10 + 01 ----- 11
Carry in second column ( from right to left)
011 + 001 ----- 100
100 + 001 ----- 101
101 + 001 ----- 110
0111 + 0001 ----- 1000
Nucleus[edit | edit source]
The nucleus of group G is :[7]
where a is an action of group G
Tree[edit | edit source]
A point of the binary tree c = c0 c1 c2 . . .where corresponds to the diadic integer
which translates to the n-ary addition
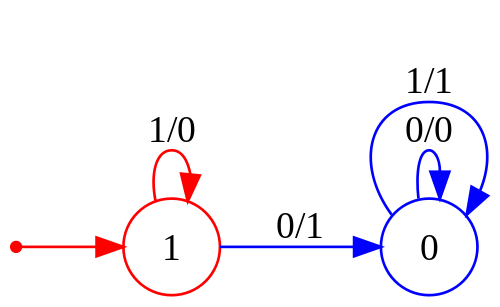
Visual representation[edit | edit source]
Diagram[edit | edit source]
Here alphabet is a set consisting of two symbols so it is called binary alphabet:
Labels shows pairs of symbols : input/output
There are 2 vertices ( nodes, states of machine) : 1 and 0.
Vertices correspond to the states .
"The states of this machine will represent the value that is "carried" to the next bit position.
Initially 1 is "carried".
The carry is "propagated" as long as the input bits are 1.
When an input bit of 0 is encountered, the carry is "absorbed" and 1 is output.
After that point, the input is just replicated." [8]
Table[edit | edit source]
Table [9]
GAP/FR[edit | edit source]
BinaryAddingGroup ( global variable )
This function constructs the state-closed group generated by the adding machine on [1,2]. This group is isomorphic to the Integers.
BinaryAddingMachine ( global variable )
This function constructs the adding machine on the alphabet [1,2]. This machine has a trivial state 1, and a non-trivial state 2. It implements the operation "add 1 with carry" on sequences.
BinaryAddingElement ( global variable )
This function constructs the Mealy element on the adding machine, with initial state 2.
These functions are respectively the same as AddingGroup(2), AddingMachine(2) and AddingElement(2).
gap>LoadPackage("fr");
gap> Draw(NucleusMachine(BinaryAddingGroup));
gap>Draw(BinaryAddingMachine);
References[edit | edit source]
- ↑ THE n-ARY ADDING MACHINE AND SOLVABLE GROUPS by JOSIMAR DA SILVA ROCHA AND SAID NAJATI SIDKI
- ↑ wikipedia : Endianness
- ↑ wikipedia : Least significant bit
- ↑ Wikipedis : carry at Binary_numeral_system
- ↑ ITERATED MONODROMY GROUPS by VOLODYMYR NEKRASHEVYCH
- ↑ Groups and analysis on fractals Volodymyr Nekrashevych and Alexander Teplyaev
- ↑ FROM SELF-SIMILAR STRUCTURES TO SELF-SIMILAR GROUPS DANIEL J. KELLEHER, BENJAMIN A. STEINHURST, AND CHUEN-MING M. WONG
- ↑ Robert M. Keller : Finite-State Machines
- ↑ wikipedia : State transition table