Fermat's Last Theorem/Print Version

The famous theorem, for n > 2 this equation does not have a nontrivial solution in whole numbers

This book will discuss one of the most famous theorems of mathematics. It will talk about that which is commonly called Fermat’s last theorem, the subject will be confronted from a principally historic point of view, the concepts and the theorems behind the proof being too complex even for the greater part of professional mathematicians. The book will follow a time based logic starting from the beginnings of mathematics up to arrival in our times, as a matter of fact having nevertheless been enunciated in 1637, the theorem has profound implications for many branches of mathematics and the premises that give birth to it begin right in the primordial days of mathematics.

Acknowledgment is given to the original version in Italian on Wikibooks of which this book is a translation.

The Theorem

The Last Theorem

Fermat's Last Theorem can be stated simply as follows:

It is impossible to separate any power higher than the second into two like powers,

or, more precisely:

If an integer n is greater than 2, then the equation aⁿ + bⁿ = cⁿ has no solutions in non-zero integers a, b, and c.

If you let n = 2, the equation takes the form used in the Pythagorean Theorem.

Since this equation can be satisfied by non-zero integers, the requirement that n be greater than 2 is necessary.

Pythagoras

The origins of numbers is sometimes thought to be lost in the meanders of human history. As a matter of fact since ancient times man has studied numbers and their properties. In the beginning the study was dictated by practical necessity (measures geometrical, astronomical, economical, etc.) but subsequently some humans began to interest themselves in the properties of numbers and sought to understand not only how to solve problems but also why certain formulae or methods always gave the correct result. This desire of abstraction, desire of exploring the more intimate nature of numbers and of their properties saw one of its greatest exponents in Pythagoras.

Pythagoras

Pythagoras (575 B.C. - 490 B.C.) - mathematician, philosopher, scientist.

During his life Pythagoras passed the years of his youth navigating the length and breadth of the Mediterranean in search of knowledge. During his travels he learnt practically all the ideas in the field of mathematics possessed by the Egyptians and by the Babylonians but, while these peoples were interested principally in the practical applications, Pythagoras wanted to understand the why of mathematics and more generally of things. After some trials and tribulations he succeeded in founding a school of philosophy, this school differently to modern centres of instruction resembled more a sect where numbers were venerated like divine entities. He who entered the school had to divest himself of all his worldly goods which went into the common purse. An obligation of absolute secrecy with respect to the uninitiated was in force and many myths and legends arose around the school.

The theorem of Pythagoras

Pythagoras is universally famous for his theorem.

Given a and b two sides of a right-angled triangle and c its hypotenuse one has:

$a^{2}+b^{2}=c^{2}\,\!$

In reality this equation was known by many other mathematicians of the era but Pythagoras became the father of it since he was the first to furnish a generic proof of the equation. He produced by means of a combination of logic and elementary geometry a proof for every right angled triangle. He then passed from an empirical proof for a finite number of cases to a proof as we currently understand it, that is a proof that it is always true for fixed preconditions. Proofs are those which differentiate mathematics from all other sciences. In sciences such as physics, chemistry, etc., the theories are based on theoretical considerations and on experimental trials but they are never considered definitive, they can always be overtaken by the evolution of knowledge. Instead in mathematics once a theorem has been proved, its veracity can no longer be open to discussion. The theorem of Pythagoras was true two thousand years ago and it will be true even in two thousand years from now. The link between Pythagoras’ theorem and Fermat’s last theorem is obvious, it is enough to substitute the power 2 with a generic power n in order to obtain Fermat’s theorem. In fact the theorem of Pythagoras is a particular case of Fermat’s theorem. Fermat was in fact studying the properties of the pythagorean triads (the solutions of the theorem of Pythagoras) when he enunciated his theorem.

Pierre de Fermat

Pierre de Fermat

Pierre de Fermat

Pierre de Fermat (1601–1665) - French Magistrate.

Although his work as a magistrate was very demanding, Fermat found the time to dedicate himself in a most profitable way to the study of Mathematics. Even though he was not a professional mathematician by training Fermat made important contributions in the study of functions and of the theory of numbers. Fermat conducted an intimate correspondence with various mathematicians of the era, but his natural reserve together with a notable reluctance in making known his discoveries resulted in his genius being discovered a long time after his death, when his son decided to collect his father’s papers and make them public. The famous enigma was idealised by Fermat while he was studying the Arithmetica of Diophantus of Alexandria, mathematician 212 A.D. to 298 A.D. Diophantus’ book collected together many elegant proofs of complete solutions to problems that mathematicians had faced over the course of centuries; reading the part concerning the Pythagorean triads, one supposes that Fermat may have had the idea of extending the power of 2 to a generic n. Fermat wrote in note in the book the enunciation of his famous theorem and then added:

---

Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caperet.

[I have discovered a truly marvellous proof of this, which however the margin is not large enough to contain.]

The unresolved theorem

Fermat was accustomed to annotating his books: many theorems were found in their margins, generally without proof. The proof of these theorems was in some cases simple while in other cases it required hard work. The last theorem in fact takes its name from the fact of being the last of Fermat’s theorems to be proved, not from the fact of having been the last to be enunciated. To be precise, rather, its name was incorrect: until 1994 when it was proved, rather than a theorem it was strictly speaking a conjecture. The majority of mathematicians however used this name: in fact they held it true though not being able to prove it, given that the majority of the affirmations of Fermat had proved themselves true. It goes without saying that these facts are not sufficient to render a conjecture a theorem, but the majority of mathematicians in this particular case passed over this detail without too many problems.

Leonhard Euler

Leonhard Euler

Leonhard Euler

$\mathbb {T}$he publication of Fermat’s writings had generated opposing opinions among mathematicians. The majority of them recognised the usefulness but the fact that the greater part of the theorems were without proof or with incomplete proofs obviously reduced the immediate usefulness of them even if some mathematicians took the theorems as challenges to face and win. Many were faced and resolved but that which subsequently would be called the last theorem resisted all attempted assaults. Leonhard Euler obtained the first results a century after Fermat. Euler was a Swiss mathematician born in 1707 in Basel and died in 1783 in St. Petersburg. Initially Euler was to have become a theologian but Johann Bernoulli became aware of the extraordinary ability of the young man and convinced his father to let Leonhard become a mathematician. This was an enormous good fortune for mathematics given that Euler’s contributions range over so many areas of mathematics and are so profound as to render Euler one of the greatest mathematicians of the XVIII century if not rightly the greatest. Euler analysing the notes written by Fermat found an outline proof of the case n=4. Fermat had written this proof within another proof. In order to prove that case Fermat made use of a technique called infinite descent, Euler sought to utilise this technique for the other cases in such a way as to find a proof for all values of n. Initially he confronted the case n=3. He succeeded in resolving this case but had to make use of complex numbers, in reality other mathematicians had sought to adapt infinite descent to the case n=3 but it took a creative person such as Euler in order to understand that complex numbers were necessary in order to obtain a valid proof. Euler also sought to resolve n=5 but without results.

Sophie Germain

Sophie Germain

After Euler's progress, for around fifty years there were no improvements notwithstanding the fact that the last theorem had become the most famous problem in the theory of numbers. This situation changed radically thanks to Sophie Germain.

Sophie Germain was born in 1776 and died in 1831 and for all her life she had to fight against prejudice. In her society it was unthinkable that a lady of good standing dedicated herself to subjects such as mathematics, but Germain when small had read a book on the history of mathematics and remained fascinated by the death of Archimedes.

The legend recounts that when a roman soldier went to call Archimedes in order to conduct him in front of the centurion Archimedes refused to follow him being occupied with a geometric problem, for this reason the soldier ran him through. Germain was so struck by the fact that a man could have lost his life for mathematics that she decided to study it. Initially her decision was much opposed by her father, but with the passing of the years he had to resign himself to the wishes of his daughter deciding to support her. Germain found it very difficult to acquire modern mathematical techniques given that her tutors did not intend to teach them to her and she, being a woman, could not attend the university where courses in advanced mathematics were held. Germain then used the stratagem of passing herself off as a monsieur Le Blanc, a student who had withdrawn from the Ecole Polytecnique. Obviously she was not able to attend lessons but utilising this false identity she succeeded in getting herself the printed notes and the problems for the students attending that she solved and presented always under the same pseudonym. In the beginning the trick worked until the course professor, the great mathematician Joseph-Louis Lagrange, wanted to know the student who furnished those so ingenious solutions. Lagrange meeting Germain was surprised but pleased by the young woman and decided to help her in her study of the material.

Germain worked for years on the theory of numbers and also interested herself in Fermat's theorem. She obtained a result that she held to be very important but wanting confirmations on the validity of her discovery she decided to contact the then greatest authority, that is to say Carl Friedrich Gauss. Gauss had not interested himself in Fermat's theorem holding the enunciation in itself without interest, but when he received the letter from Germain he remained so impressed by her result as to dedicate himself to the problem and to confirm to Germain the validity of her method. Germain's idea was based on the use of a particular typology of prime numbers that were subsequently called Sophie Germain's prime numbers. For these prime numbers Germain succeeded in demonstrating that solutions of Fermat's theorem probably did not exist. Probably it meant that these eventual solutions would have had some properties so particular as to render the existence of these numbers difficult. Some of her colleagues analysing the problems defined by these prime numbers succeeded in proving that solutions did not exist for some of them, such as 5 or 7. Subsequently Gauss abandoned the theory of numbers in order to dedicate himself to applied mathematics and Germain without further support in the field of mathematics decided to concentrate on physics, where she made important contributions in the study of elastic vibrations.

Gabriel Lamé and Augustin Louis Cauchy

Gabriel Lamé and Augustin Louis Cauchy

Picture of Cauchy

Sophie Germain’s results appeared to many to be the turning point, and that the definitive solution of the enigma was close. The French Academy of Science offered a series of prizes to whoever succeeded in proving Fermat’s last theorem. In that epoch the offer of prizes for the solution of mathematical enigmas was a common practice followed by many academies, given that one was thus able to direct the research of many scientists into specific areas of knowledge. These prizes were used whether for research into the solutions of practical problems or for the solution of theoretical problems such as Fermat’s theorem. The mathematicians Gabriel Lamé and Augustin Luis Cauchy announced being on the point of proving the theorem utilising similar techniques. These mathematicians set the Parisian salons on fire with statements and extracts of their respective proofs but without ever publishing the complete proofs. This situation dragged on for the whole of the month of April 1847 until the mathematician Joseph Liouville read to the academy of science a letter from the mathematician Ernst Eduard Kummer. Kummer analysing the few pieces of evidence on the proofs of Cauchy and Lamé had become aware that the proofs followed the same reasoning and that they contained a logical error that rendered them fallacious. Kummer had become aware that the two mathematicians had based their proof on a property known as unique factorisation. This stated in substance that every integer number could be broken down into a single series of prime numbers. Known since the times of Euclid (fourth century B.C.) it was used in very many proofs and is so important that the theorem that enunciated it is called the fundamental theorem of arithmetic. The problem was that the proof of Cauchy and Lamé utilised complex numbers and, in the field of complex numbers, this property is not necessarily true. The lack of unique factorisation could have been worked round with some techniques but however there remained some recalcitrant numbers. These numbers could in theory have been faced singly, but being infinite that would not have resolved the problem. Lamé became aware of the impossibility of finding a general solution, while Cauchy held his implementation not so dependent on factorisation and worked for several weeks on the subject before giving up. Finally, in 1856, seeing that no correct solution had been presented to the academy, it decided to withdraw the prize. It still in fact lacked 138 years to the final solution.

Paul Wolfskehl

Paul Wolfskehl

The works of Kummer on the factorisation of complex numbers threw a general mistrust on the possibility of finding a proof of Fermat’s theorem in a reasonable time. The researches also halted because of the birth of new branches of mathematics that drew the studious away from the theory of numbers. Wolfskehl was a German industrialist from Darmstadt who came from a very rich family dedicated to patronage of the arts. Paul had studied at mathematical university and, although he had greater success in business than in mathematics, his contribution was decisive in reawakening interest in the theorem. Wolfskehl at that period was in love with a woman who refused his every attention. Driven by despondency Wolfskehl had decided to commit suicide at the stroke of midnight, but being a meticulous and precise person he had planned everything and had provided an adequate arrangement of his affairs and a salutation of his closest friends by means of letters. Wolfskehl had finished the preparations before midnight and in order to pass the time began to thumb through some texts on mathematics. In particular thumbing through the work of Kummer he noted an unproved assumption. If that assumption revealed itself in reality false perhaps it would have reopened the possibility of proving Fermat’s theorem with the method of Lamé or of Cauchy. Wolfskehl worked all night and finally succeeded in proving that the assumption was true and therefore the proof was correct. This was bad news for the mathematician but Wolfskehl was so happy to have been able to correct the great Kummer that he regained faith in himself. He abandoned the proposal of suicide and instead wrote a second will according to which he would have left a good part of his patrimony to whoever was able to prove Fermat’s theorem. The will became operative in 1908 and the Royal Society of Science of Göttingen became the organisation proposed for the verification of proofs that aspired to the prize. The prize was announced by all the European mathematical publications and thousands of aspiring mathematicians choked the university of Göttingen with presumed proofs of Fermat’s theorem. Unfortunately the prize did not attract many serious mathematicians, given that these were well aware of the extreme difficulty of the problem and therefore it did not produce a real turn-about in the field of mathematics, but it had the merit of rendering the problem of Fermat’s last theorem famous to the public at large.

Andrew Wiles

Andrew Wiles

Andrew Wiles

Andrew Wiles was born in the UK, the 11th of April 1953. From a young age he demonstrated a strong interest in mathematical enigmas and problems. When he was still a small child he loved to go into public libraries in search of books containing problems and enigmas. At the age of 10 years he found in a library the book The Last Problem by Eric Temple Bell. In this book the author described what came to be known as Fermat's Last Theorem from the Greeks up to the discoveries at the end of the 1800s. The young Wiles remained fascinated by the problem. An equation so simple to enunciate had eluded some of the most able mathematicians of the world and the boy then began to fantasise hoping to find the elementary proof that had eluded the others. Wiles hypothesised that Fermat did not have a knowledge in the mathematical field superior to his own and he therefore sought a proof with his limited knowledge. Obviously he was not able to find it, he would pursue Fermat’s Last Theorem for a good part of his life. Wiles became a professional mathematician and had to temporarily abandon his quest since finding a proof was thought to be too difficult for a young mathematician and that he didn’t hold that it could produce interesting mathematics in the immediate future. Wiles’ dissertation advisor was John Coates, and he directed Wiles in the study of elliptic curves. That was Wiles’ good fortune, since Wiles' was able to use his knowledge of elliptic curves to the proof of Fermat’s Last Theorem.

Elliptic curves and modular arithmetic

Specifically Wiles analysed some elliptic curves in modular arithmetic. While classic arithmetic deals with an infinite number of numbers, in modular arithmetic one utilises only a subset of values. Modular arithmetic was also called clock arithmetic, given that this utilised a modular arithmetic with modulo equal to 24. Everyone knows that if it is 18 hundred and one waits for 8 hours one does not find oneself at 26 hundred but at 2 hundred, given that when the clock arrives at 24 it starts to count again from 0. Modular arithmetic is a complete arithmetic like that classic, only that the numbers utilised are limited. Modular arithmetic furthermore has at its disposal some very interesting properties that render it particularly useful in some fields of mathematics. When a mathematician analyses an elliptic curve with modular arithmetic he extracts a series of solutions that are called L-series. Wiles worked much on elliptic curves and on their L-series accumulating experience that would become useful to him in the future.

The Taniyama-Shimura Conjecture

Towards the end of the 1950s the Japanese mathematicians Yutaka Taniyama and Goro Shimura formulated a conjecture known as the Taniyama-Shimura conjecture. This conjecture stated that every L-series of an elliptic curve could be associated with a specific M-series of a modular form. In substance this conjecture asserted that every modular form could be put in bi-unequivocal correspondence with an elliptic curve or, given in other terms, the modular forms and the elliptic curves were the same mathematical object seen from different points of view. This conjecture from the point of view of a mathematician is very important, in fact, if it were proved true, it would have meant that problems of elliptic curves centuries old would be able to be transferred into their modular forms and tackled with new mathematical tools. Obviously the converse would also be valid.

The convention of 1984

In 1984 a event happened that revolutionised the life of Wiles: during a convention in Germany Gerhard Frey demonstrated that whoever proved the Taniyama-Shimura conjecture would also automatically have proved Fermat's last theorem. Frey showed with a series of not too complex steps that in a hypothetical counterexample to Fermat's theorem (that is a valid solution of the equation aⁿ+bⁿ=cⁿ) one would be able to write it as an elliptic curve so particular and atypical as not to be able to be associated to any M-series of a modular form. Therefore proving the Taniyama-Shimura conjecture proved that this degenerate equation did not exist and that therefore Fermat's theorem was true. In reality almost everything tied to Fermat's theorem is not as simple as it seems, so much so that the development of a proof that tied Fermat's Last Theorem in an indissoluble manner to the Taniyama-Shimura conjecture caused the mathematicians of half the world to struggle for more than two years, and in fact Frey's initial proof was incomplete.

The secret work

In 1986 Wiles came to know that the link between the Taniyama-Shimura conjecture and Fermat's Last Theorem had been demonstrated. This seemed to Wiles a golden opportunity to use advanced mathematics (seeking to prove the Taniyama-Shimura conjecture) to attain the mathematical ambition of his life (proving Fermat's Last Theorem). Wiles decided to work in absolute secrecy, contrary to the prevailing ethos. While in many disciplines it is common when working on a project to maintain strict secrecy, in order to protect patent rights, in mathematics one follows the opposite approach. Mathematicians talked among themselves constantly, successive comparison is an optimum method for facing problems that seem insoluble and in theoretical mathematics the problem of the industrial secret practically does not exist. Wiles prepared himself carefully, he abandoned all his non-obligatory duties, took an impressive research that he was about to publish, divided it into a good number of articles in such a way as to be able to furnish a constant flux of works while he was working on the conjecture and sought to assimilate as much as possible on modular forms and elliptic curves. Wiles revealed the secret of his work only to his wife. In the first two years of work Wiles made progress utilising the group theory of Galois, although he was still a long way from the solution. The 8th of March 1988 Wiles was stunned to read in the Washington Post that the Japanese mathematician Yoichi Miyaoka had proved Fermat’s conjecture. In reality Miyaoka had not produced a complete proof but utilising differential geometry, a new branch of geometry he had put forward some optimum bases for the definitive solution. Unfortunately for Miyaoka his proof had a gap that although at the beginning did not appear grave, subsequently proved itself to be catastrophic and rendered it impossible to carry out a proof of Fermat’s Last Theorem using that technique. Finally Wiles, utilising a method called Kolyvagin-Flach, succeeded in associating a particular elliptic curve to its modular form. The problem for Wiles was that the method could not be extended to all elliptic curves. Wiles then classified all the elliptic curves into families and modified the method in such a way as to adapt it to single families.

Wiles, in order to utilise the Kolyvagin-Flach method, had to profoundly expand his knowledge of algebraic geometry and not being very expert decided in the end to confide himself to a trusted mathematical expert in the sector. Therefore Wiles contacted Nick Katz, a mathematician in his department. Given that the proof was very complex and voluminous an informal discussion in Katz’s study would not have been sufficient in order to sort out all the doubts, the two decided therefore to disguise their meetings as some post graduate lessons. Wiles would have given the lessons while Katz would have participated among the public. Wiles presented the lessons in a very technical and boring manner in such a way as to eventually discourage students. In fact after a few weeks only Katz remained of the class. Wiles thanks to the help of Katz went over his proof again which effectively seemed correct. Finally Wiles working speedily eliminated the remaining families and finally in May 1993 Wiles finished the proof laying low even the final recalcitrant family.

The Cambridge conference

At the end of June at Cambridge a conference was held on L-functions and their arithmetic. In this context, surrounded by some of the most brilliant mathematicians of the planet Wiles presented his proof in a series of three conferences. The 23rd of June the third and final conference took place and a lengthy applause concluded Wiles’ final conference. Fermat’s Last Theorem had been proved. All the world’s papers spoke of the event and in an afternoon Wiles became the most famous mathematician on the planet.

An error and its resolution

Wiles sent the proof to a journal in such a way that the editor of the journal could subject the proof to verification by a qualified commission. The editor of the journal, given the importance and complexity of the proof, subdivided the sheaf into six parts and entrusted them to as many commissioners. These analysed the manuscript piece by piece and contacted Wiles in order to obtain clarifications on unclear passages and presumed errors. One of the commissioners was Katz, the same mathematician that Wiles had contacted in order to verify the correct application of the Kolyvagin-Flach method. Unfortunately for Wiles, Katz identified an error. Initially it seemed one of the many errors of little account that stud a complex proof. These errors are comparable to oversights and usually they are corrected in the space of a few hours but that error even if very subtle was also very insidious, in fact Wiles did not succeed in eliminating it. With the passage of time ever more persistent news of the gap spread within the mathematical community and also in the general papers such as the New York Times. Finally Wiles by means of e-mail communicated to the mathematical community that effectively there was a gap in the proof but that he expected to be able sort it out in a few weeks. After months of not being able to do so, and on the advice of a friend he decided to get help from an expert on the Kolyvagin-Flach method and he therefore contacted Richard Taylor. Taylor was one of the reviewers of the proof and was an ex-student of Wiles. They worked on the problem for many months, and towards the end of summer Wiles was demoralised to such a point as to propose to Taylor publicly declaring defeat, but Taylor convinced him to persevere at least until the end of September. The 19th of September Wiles was analysing the Kolyvagin-Flach method seeking to understand why the method failed when he became aware that, although the method was insufficient in order to obtain a proof, it permitted a method called Iwasawa’s method to function. Iwasawa’s method had initially been utilised by Wiles for the proof but had been abandoned as insufficient. The same method, instead, utilised in conjunction with the Kolyvagin-Flach method, furnished a valid proof.

The proof

The 25th of October Wiles gave two manuscripts to the press, in the first there was the proof of Fermat’s Last Theorem and it carried his signature. The second manuscript specified some properties of some elliptic curves and was signed by Wiles and Taylor. The second manuscript served to prove a fundamental passage of the first manuscript. The publication of the manuscripts put an end to one of the most complex and difficult proofs that mathematics had ever developed. Wiles and Taylor did not totally prove the Taniyama-Shimura conjecture, in fact the proof for all the cases arrived in 1999 by Christophe Breuil, Brian Conrad, Fred Diamond, and the same Taylor, that starting from the work of Wiles incrementally proved the remaining cases.

Appendix

This appendix collects some proofs and studies in depth some mathematical concepts that can be interesting in order to examine in depth some aspects of the book. It seeks to maintain a simple approach but the proofs being correct, in some cases however it was necessary to make recourse to some non immediate concepts and passages that have been specified and clarified where possible.

Pythagoras’ theorem

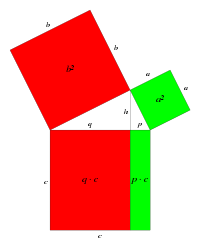
Being one of the most noted theorems in the history of mathematics, many proofs exist, the work of astronomers, stockbrokers, and even one by Leonardo da Vinci. Probably, together with quadratic reciprocity, it contends for the prize for the theorem with the most absolute proofs. It will be proved in a graphical manner utilising only the concepts of elementary geometry. Pythagoras’ proof will not be quoted being very complex and not immediate.

The proof is very simple, as one sees from the graphic one constructs first a square formed by four triangles and by two squares, one of side a and the second of side b. The area of a square is calculated multiplying the side by itself or in modern notation the area is the side raised to the power two. The area of the large square is therefore the sum of the areas of the squares values a² and b² plus the sum of the four triangles. In the second square we have again four triangles and a square of area c². The four triangles being present both to the left of the equality and to the right can be eliminated. Therefore remaining in the equation:

a² + b² = c²

As one wished to prove. It is to be noted that the proof is generic and effectively covers every possible right angled triangle given that numbers are not utilised in the proof but only generic segments length a, b and c. The proof depends solely on the fact that the triangles are right angled and on the fact that one is utilising Euclidean geometry. This is a small gallery of some geometrical proofs of the theorem even if as was said above there are very many proofs and in fact there are also purely algebraic proofs, proofs that utilise complex numbers and even proofs written in the form of sonnets.

Fundamental theory of arithmetic

The fundamental theory of arithmetic states that every natural number that is not 1 admits one and only one factorisation in prime numbers not taking account of the order of the factors. (The exclusion of 1 is due to the fact that it does not have prime factors.) This theorem was the basis of the proofs of Gabriel Lamé and Augustin Luis Cauchy and as was said in general is not valid for complex numbers therefore it cannot be utilised for Fermat’s theorem but given its importance it was decided however to include the proof in the appendix. The statement is easily verifiable for “small” natural numbers: it is easy to discover that 70 is equal to 2 × 5 × 7 while 100 equates to 2 × 2 × 5 × 5 or 2² × 5², and furthermore it is easy to verify that for these numbers other decompositions into prime factors cannot exist. Conversely the general proof is rather longer: Here is an extract of it. It deals with a proof for absurd: that is it starts from the hypothesis contrary to that of the statement in order to be able to prove it unfounded.

One supposes that there exist some number reducible into prime factors in more than one way, and one calls the smallest m. Firstly one proves that, given two factorisations of m, the prime numbers that present themselves in the first factorisation are all distinct from those in the second factorisation. They are in fact two different factorisations:

[1]

$m=p_{1}p_{2}p_{3}\dots p_{s}$

[2]

$m=q_{1}q_{2}q_{3}\dots q_{t}$

where p_i and q_j are prime. (Note: within a single factorisation there can be repeated factors, naturally: for example, 100 = 2 × 2 × 5 × 5). Were there to be an identical factor p_h = q_k, we could divide m by such a factor and obtain a number m' , less than m, that would also itself have two distinct factorisations. At this point we know that p₁ is different from q₁; without loss of generality we can suppose that p₁ < q₁. We put then

[3]

$n=(q_{1}-p_{1})q_{2}q_{3}\dots q_{t}$

Evidently, n < m, given that [3] can be written as:

[4]

$n=q_{1}q_{2}q_{3}\dots q_{t}-p_{1}q_{2}q_{3}\dots q_{t}=m-p_{1}q_{2}q_{3}\dots q_{t}\;\!$.

We now demonstrate that n admits at least two distinct factorisations. We begin by considering if the first factor of n, q₁ - p₁, can or cannot be prime; in the case that it was not, we suppose factorising it. The factorisation of n thus obtained does not admit p₁ among its factors. In fact, from the first part of the proof, we know that p₁ is different from q₂, q₃, ..., q_t; but it cannot none the less appear in the eventual factorisation of q₁ - p₁. If in fact it happened that would mean that

$q_{1}-p_{1}=p1\cdot b\Rightarrow q_{1}=p_{1}(1+b)$

and therefore q₁ would be divisible by p₁, which is not possible in as much as q₁ is a prime number. Taking now the final equality [4] and substituting for m the value from [1], we obtain:

[5]

$n=p_{1}p_{2}p_{3}\dots p_{s}-p_{1}q_{2}q_{3}\dots q_{t}\rightarrow n=p_{1}(p_{2}p_{3}\dots p_{s}-q_{2}q_{3}\dots q_{t})$

In whatever way the second factor in [5], may be factorised, we will have obtained a factorisation of n that contains p₁, and that therefore is different from that in [3], contrary to the hypothesis that m was the smallest number that admitted more than one factorisation. The theorem is therefore proved.

Principle of Induction

The Principle of induction states that

If $U$ is a subset of the set $\mathbb {N}$ of natural numbers that satisfy the following two properties:

• $U$ contains $0$,
• every time that $U$ contains a number $n$ $U$ contains also the successive number $n+1$,

then $U$ coincides with all of the set of natural numbers $\mathbb {N}$

This is found in general within the axioms of Peano and furnishes a potent instrument for proofs in all sectors of mathematics. In the book it is recalled at times given that many mathematicians have sought to prove a base case of Fermat's theorem and then of generalising the solution in order to be able include therein the successive cases by means of this principle.

Proof by induction

In order to prove that a certain assertion $P(n)$ in which appears a natural number $n$ valid for whatever $n\in \mathbb {N}$ one must apply the principle of induction in the following way:

One puts $U=\{n\in \mathbb {N} :{\mbox{vale }}P(n)\}$,

1. one proves $P(0)$ as valid, that is that $0$ is in the set of natural numbers $U$ for which $P(n)$ is valid;
2. one assumes as a hypothesis that the assertion $P(n)$ may be valid for a generic $n$ and from such an assumption one also proves that $P(n+1)$ (that is that $n\in U\Rightarrow n+1\in U$)

and therefore one concludes that the set $U$ of numbers for which $P(n)$ is valid is valid coincides with all the set of natural numbers. Point 1 is generally called base of the induction, point 2 the inductive step.

The following is an intuitive mode in which one can look at this type of proof: if we have available a proof of the base $P(0)$ of the inductive step $P(n)\Rightarrow P(n+1)$ then clearly we can make use of these proofs in order to prove $P(1)$ using the logical rule modus ponens on $P(0)$ (the base) and $P(0)\Rightarrow P(1)$ (which is a particular case of the inductive step for $n=0$), then we can prove $P(2)$ since now we are using the modus ponens on $P(1)$ and $P(1)\Rightarrow P(2)$, thus for $P(3)$, $P(4)$, etcetera... it is clear at this point that we can produce a proof in a finite number of steps (eventually very lengthy) of $P(n)$ for whatever natural number $n$, from which we deduce that $P(n)$ is true for every $n\in \mathbb {N}$.

An example

We will prove that the following formula is valid:

For every $n\in \mathbb {N}$: $0+1+2+3+4+...+n={\frac {n(n+1)}{2}}$

In this case we have $P(n)\quad \equiv \quad 0+1+2+3+4+...+n={\frac {n(n+1)}{2}}$.

• Base base of the induction: we have to prove the assertion $P(n)$ is true for $n=0$, and so, substituting, that $0={\frac {0\cdot 1}{2}}$, and in effect there is very little work, one is talking of an elementary calculation;
• Inductive step: we must show that for every n the implication $P(n)\Rightarrow P(n+1)$ is valid, that is, substituting:

$0+1+2+3+4+...+n={\frac {n(n+1)}{2}}\quad \Rightarrow \quad 0+1+2+3+4+...+n+(n+1)={\frac {(n+1)((n+1)+1)}{2}}$

Therefore we must assume as true

$P(n)\quad \equiv \quad 0+1+2+3+4+...+n={\frac {n(n+1)}{2}}$,

working on this equality and concluding with the analogous equality for $n+1$: We could for example add $n+1$ to both sides of the equality P(n):

$0+1+2+3+4+...+n+(n+1)={\frac {n(n+1)}{2}}+(n+1)$,

then we make some simple algebraic steps:

$0+1+2+3+4+...+n+(n+1)={\frac {n(n+1)}{2}}+{\frac {2(n+1)}{2}}$,

$0+1+2+3+4+...+n+(n+1)={\frac {(n+1)(n+2)}{2}}$,

$0+1+2+3+4+...+n+(n+1)={\frac {(n+1)((n+1)+1)}{2}}$

and this final equality is exactly $P(n+1)$. This concludes the proof of the inductive step.

Having therefore proved the base of the induction and the inductive step we can conclude (from the principle of induction) that $P(n)$ must be true for every $n\in \mathbb {N}$.$\square$

Modular Arithmetic

Modular arithmetic (sometimes called clock arithmetic since the calculation of the hours in cycles of 12 or 24 is based on such principle) represents an important branch of mathematics. It finds applications in cryptography, in the theory of numbers (in particular in the research of prime numbers), and it is the basis of many of the most common arithmetical and algebraic operations. It deals with a system of integer arithmetic, in which the numbers "wrap round on themselves " every time that they reach multiples of a specific number n, called the modulo. Modular arithmetic was formally introduced by Carl Friedrich Gauss in his treatise Disquisitiones Arithmeticae, published in 1801. Modular arithmetic is based on the concept of congruence modulo n . Given three whole numbers a, b, n, with n≠0, we say that a and b are congruent modulo n if their difference (a−b) is a multiple of n. In this case we write

$a\equiv b{\pmod {n}}$

and we say that a is congruent to b modulo n. For example, we can write

$38\equiv 14{\pmod {12}}$

since 38 − 14 = 24, which is a multiple of 12. In the case that both numbers are positive, one can also say that a and b are congruent modulo n if they have the same remainder from division by n. Therefore we can also say that 38 is congruent 14 modulo 12 since both 38 and 14 have remainder 2 after division by 12.

Properties of congruence

Congruence is a relationship of equivalence between integer numbers as one sees from the following properties:

• Reflexive property: every number is congruent to itself modulo n, for every n different from fixed 0.

$a\equiv a{\pmod {n}}\qquad \forall a\in \mathbb {N} ,\forall n\in \mathbb {N} _{0}$

Proof: one has a - a = 0. But as is noted, every non-zero integer is a divisor of 0. Therefore n divides (a - a)

• Symmetrical property: if a is congruent to b modulo n then b is congruent to a modulo n

$a\equiv b{\pmod {n}}\Rightarrow b\equiv a{\pmod {n}}\qquad \forall a,b\in \mathbb {N} ,\forall n\in \mathbb {N} _{0}$

Proof: if n divides (a - b), then n also divides the opposite (b - a) = - (a - b

• Transitive property: if a is congruent to b modulo n and b is congruent to c modulo n then also a is congruent to c modulo n.

$a\equiv b{\pmod {n}}\quad \land \quad b\equiv c{\pmod {n}}\Rightarrow a\equiv c{\pmod {n}}\qquad \forall a,b,c\in \mathbb {N} ,\forall n\in \mathbb {N} _{0}$

Proof: if n divides (a - b) and n divides (a - c) then, because of the distributive property of the division with respect to the subtraction, n also divides [(a - c) - (a - b)]=[a - c - a + b] = (b - c).

Invariance with respect to arithmetical operations

Another important characteristic of the relationship of congruence is the fact of being preserved by the usual arithmetical operations between integers:

• Invariance by addition: increasing or reducing two numbers congruent modulo n by the same quantity, the new numbers obtained are still congruent between themselves modulo n. More synthetically

$a\equiv b{\pmod {n}}\Leftrightarrow (a+c)\equiv (b+c){\pmod {n}}\qquad \forall a,b,c\in \mathbb {N} ,\forall n\in \mathbb {N} _{0}$

Proof: we write (a - b) = (a - b + c - c) = (a + c) - (b + c)

• Invariance by multiplication: multiplying two numbers congruent modulo n by the same quantity, the new numbers obtained are still congruent between themselves modulo n.

$a\equiv b{\pmod {n}}\Rightarrow a\cdot c\equiv b\cdot c{\pmod {n}}\qquad \forall a,b,c\in \mathbb {N} ,\forall n\in \mathbb {N} _{0}$

Proof: if n divides (a - b) then n divides (a - b)×c

Note: One can only invert this property if n does not divide c, that is if c is not congruent to 0 (modulo n).

• Invariance with respect to raising to a power: raising two numbers congruent modulo n to the same power k, the numbers obtained are still congruent between themselves modulo n.

$a\equiv b{\pmod {n}}\Rightarrow a^{k}\equiv b^{k}{\pmod {n}}\qquad \forall a,b,c\in \mathbb {N} ,\forall k\in \mathbb {N} ,\forall n\in \mathbb {N} _{0}$

Proof: if a ≡ b ≡ 0 (mod n) the proposition is banal. If a ≡ b (mod n) is non null, we suppose to know that $a^{k-1}\equiv b^{k-1}{\pmod {n}}$. Multiplying both the terms by a thanks to invariance by multiplication, we will have $a^{k}\equiv b^{k-1}\cdot a{\pmod {n}}$. We start now from the congruence a ≡ b (mod n) and we multiply both the members by $b^{k-1}{\pmod {n}}$, thanks always to invariance by multiplication. We obtain:$a\cdot b^{k-1}\equiv b^{k}{\pmod {n}}$. Comparing the two expressions, and utilising the symmetrical and transitive properties, one deduces that $a^{k}\equiv b^{k}{\pmod {n}}$. Since the proposition is true for k = 1 and the fact that it may be true for k-1 implies that it is true for k, by the principle of induction the proposition is true for every k.

Note: This property can be inverted only if k is not 0.

Bibliography

Bibliography

The development of this short book is based principally on the book: Fermat’s last theorem by Simon Singh ISBN 88-17-11291-7.

The book is an explanatory text that, like this small volume, retraces the history of the theorem. The book studies in depth the history of the scientists who encountered Fermat’s theorem even in an indirect way and studies in depth in a clear manner the fundamental mathematical aspects without becoming excessively technical.

For the realization of this book pages from Wikipedia were also used as reference regarding Fermat’s Theorem, the bibliographies of the scientists listed in the book and the mathematical subjects discussed in the book. The appendix is based almost entirely on articles from Wikipedia. In particular the articles on Pythagoras Theorem, the Principle of Induction, the Fundamental Theorem of Arithmetic and the article on Modular Arithmetic were used to realize the chapters.

Translation History

This book has been translated from the original Italian version by User:Adriano.