Electronics/Transformer Design



Practical transformer design requires knowledge of electrical principles, materials, and economics. Small transformers, under 10 kVA, may be designed using handbook data and pencil-and-paper calculations, but larger or mass-produced units are often designed with extensive computer aided modeling (CAM). and finite element analysis (FEA). However, CAM and FEA are still based on Maxwell's equations, Ampere’s law, Faraday’s law, and Gauss’s law, which together with Lenz’s law, are the basis of magnetic circuit analysis. Ref:[1][2]. Other computer aided design (CAD) software exists that use the basic equations, and it is used by smaller manufacturers. However, all of this software still has to adhere to Maxwells' equations, and the before-stated electrical/magnetic laws, which are the basis for all transformer and magnetics design.
Power transformer design[edit | edit source]
The designer first needs several known factors to design a transformer. For a transformer using a sine or square wave, one needs to know the incoming line voltage, the operating frequency, the secondary voltage(s), the secondary current(s), the permissible temperature rise, the target efficiency, the physical size one can use, and the cost limitations. Once these factors are known, design can begin.
Initial calculations[edit | edit source]
The designer first starts with the primary voltage and frequency. Since they are a known factor, they are the first numbers to be plugged into the equations. One then will find the power in watts (or volt-amperes) of each secondary winding by multiplying the voltage by the current of each coil. These are added together to get the total power the transformer must provide to the load(s).


The transformer losses in watts are estimated and added to this sum to give a total power the primary coil must supply. The losses are from wire resistance (I2 R loss), loss in the core from magnetic hysteresis and from eddy currents. These losses are dissipated as heat. Here, the permissible temperature rise must be kept in mind. Each type of core material will have a loss chart whereby one can find the loss in watts per pound by looking up the operating flux density and frequency. Next, one selects the type of iron by what efficiency is stated, and the value of losses to the user. Once the iron is selected, the flux density is selected for that material.
Type of iron (electrical steel)[edit | edit source]
The relative permeability (μr) of a magnetic material is essentially how easy it will become magnetized. In this case, one looks for a core material with high permeability and a high flux density. Of course, the better each become, the material goes up in price due to the manufacturing cost of the material, and their different compositions. Some basic values of relative permeability for electrical steel are: SiFe unoriented 400, SiFe oriented 1500, 50-50 NiFe oriented 2000, and 79 Permaloy 12,000 to 100,000. In other words, a grain-oriented silicon steel conducts magnetic flux 1500 times better than a vacuum. Ref:[3].


Each type of iron (steel) has a maximum flux density it can be run at without saturating. The designer refers to B-H curves for each type of steel. They select a flux density where the knee either starts on the curve, or slightly up on it. The start of the knee is where saturation starts and permeability is at its highest. As saturation starts, the permeability curve starts dropping off rapidly to zero, and the primaries inductance falls rapidly. By selecting this point on the knee, it will give a transformer with the lowest weight possible for that material. The curve shows that as saturation begins, the magnetic field strength in Oersteds (H) raises rapidly as compared to any increase in flux density (B), and so will the ampere turns. When using the equations, the two most important are the number of turns (N), and the core area (a). One needs to find the core area in square centimeters or inches, and match it to the total power in watts or volt-amperes. The larger the core, the more power it will handle. Once this core size is calculated, one then finds the number of turns for the primary. One then is looking at a transformer whose primary voltage will cause a flux density of a specified amount due to the number of turns in a certain type/size of core.
For sine wave operation, the designer then uses either the two short formulas, or they begin using the long formulas which are more exact, and whereby all the factors can be changed. For square wave operation, refer to the notes at the end of the equations section. Either way, it's time to use a transformer design sheet. The design sheet has places to write the details such as the flux density, the number of turns, calculate the turns per layer, and thickness of the coil.
Secondary turns calculation[edit | edit source]
Once the number of turns of the primary are calculated, the secondary windings numbers can be calculated with the same turns per volt figure. If the primary has 120 turns for 120 volts input, we would have 1 turn per volt. If we needed a 12 volt secondary, then we would require 12 turns on it. This is for a perfect transformer without losses though.
In reality, there are losses that have to be added, as the 12 turn coil will not produce 12 volts under load, but a lower voltage. A rule of thumb is to allow for 5% in losses. (Transformers below 300w often have higher regulation losses). In this case, we would multiply the 12 turns by 1.05 to get a new number of turns equaling 12.6 turns. Since fractional turns are not possible for line frequency transformers, 13 turns would be used. It is best to have a slightly higher voltage than one too low. Beware, smaller transformers which have a higher turns per volt, have higher losses, and the efficiency drops as the size goes down.
The turns per volt figure typically varies from 1 to about 4, with around 4 turns per volt common for small appliance transformers, and around 1 turn per volt used for intermittent duty fan cooled microwave oven transformers. Volts per turn is commonly used for larger transformers, since they are less than one turn per volt, or as an example, 1/2 turn per volt, or 'two volts per turn'. Distribution transformers are often limited by excessive insulation required between each turn, thus they are ran at high flux densities and oil cooled.
Here is where trial and error still comes into transformer design. Since the primary coil has to be wound with a wire that is large enough to handle the total power the transformer will handle at a certain flux density, and the secondary or secondaries have to be wound with heavy enough wire for their loads, the finished coil must still fit within the core's windows once the overall size is calculated after adding the bobbin and paper thickness of each layer. Most of the time, the design has to be modified or adjusted several times over this, because the coil is too big for the windows. If the coil does not fit, there are a few options. A larger core with larger window openings having the same core area can be used, or the flux density can be raised by reducing the turns on the primary. Once these turns are reduced, the turns in the secondary will be reduced. This since the number of volts per turn in the primary equal the number of volts per turn in the secondary minus losses. However, this is at the expense of raising the flux density, the magnetizing current, the temperature, and lowering the efficiency. It's much better to select a larger core which has larger windows to accept the coil. The depth or thickness of the new core can be adjusted to equal the old core area in square centimeters or square inches. This measurement is the cores tongue width multiplied by its depth or thickness. As the core size goes up, so does the tongue width, which would add to the core area.
Thickness of coil windings[edit | edit source]




When calculating the coil thickness, several things need to be considered. The voltage that each winding sees will determine the wires insulation thickness. Once this voltage is known, the diameter of the selected insulated wire can be used. By knowing the wire diameter, the number of turns per layer can be calculated, and the number of layers by using the window height and winding margins. The windows are the openings on either side of the core. The window area is simply found by multiplying the window width by its height. Next, one adjusts the thickness of the insulation paper for the layers of each winding due to the voltage between the coils. This thickness is added to the total coil thickness by multiplying the paper thickness by the number of layers. The paper that separates two different windings is always thicker than the layer paper to match the voltage difference between the windings and must support the wire. Last, the bobbin, (13B on drawing), thickness is added. All is then added to the design sheet and the total calculated. This total thickness is compared to the window dimensions for a fit. The design should not exceed 80-85% of available opening to allow for manufacturing tolerances. In certain circumstances, it may be better to reduce the number of windings in the coil, and use another smaller transformer to supply them. This can actually save money in the long run by reducing the possibility of coil failure over heat.
A smaller coil with few layers is always recommended. A coil with a large number of layers will run hotter than one with a few. Each winding has a "hot spot" which is always located mid-way at its center. If the winding has a number of layers, the heat will increase at this hot spot. The hot spot is almost always where the winding will fail due to heat. The heat from each winding has to travel through each layer and is dissipated from the outside of the coil. This means that the winding, (13 on drawing), closer to the core, (12 on drawing), will be hotter than the outer ones. Since this is the case, and most of the time the winding closest to the core is the primary, the largest wire that will fit for the current drawn should be used. The exception to having the primary here is using a winding with very small diameter wire. Since the coil will expand due to heat, a small wire coil on the outside could break because of the expansion. Being at the core, it would expand less and not break the wire. Most small bias windings, rated at a few milliamperes, and used in vacuum tube circuits are wound in this manner. A good rule of thumb is to use 1000 circular mills per ampere for the wire selection, when designing the primary winding. (in metric units half a square mm per amp) This value should be reduced for small transformers wound with fine wire - for example a 10VA transformer may have a 55C rise in temperature at half this value (one square mm per amp), while a 100VA transformer could withstand 750 circular mills per ampere ( ~0.7 square mm per amp) for a similar temperature rise.
It should be noted that some small transformers fail, when the wire coming up from the bottom of the coil, breaks near the terminal post. This could be due to expansion of the coil, or from the connection between the wire and terminal not being soldered properly.
Referring to the transformer sectional cooling drawing in this section, the spacer, (14 on drawing), is added to each side of the coil to separate the two windings, thus allowing a cooling vent to cool the coils. This is done in some small power and large distribution transformers. There is also a special insulation paper that has wood slats glued to the surface to hold the windings apart. If the windings are separated completely, it also raises the electrical insulation between the two windings by adding an air gap.
For using a two section bobbin (for a two winding transformer), the above is not necessary. These are used by jumble or random winding the wire on each section of the bobbin. Jumble-winding by definition means that the wire is wound on the bobbin in a random way without layers separated by paper. However, the amount of wire used for each winding has to fit within the bobbin so it too will fit inside the cores windows. Most small transformers are manufactured this way to save cost, as it would be very difficult to neatly stack extremely fine wire.

Insulation[edit | edit source]
The insulation materials used in transformer construction varies, but are mainly the finish applied to the laminations, varnish or coated insulation on the wire, paper (fish paper, crepe paper, etc.), or plastic film for the coil, cardboard or plastic for the bobbin, and the varnish that the completed transformer is dipped into at the end of construction. Though this all works well for electrical insulation, it is also a thermal insulation, and causes the coil to hold in heat. This being the case, the thinnest insulation should be used that will supply the correct electrical insulation for the transformer.
The varnish dip that is applied, is generally done in a vacuum chamber. Most varnish is a clear color, but some is dyed black. The vacuum atmosphere assures that the coil is totally saturated with varnish, as the vacuum removes any bubbles or air pockets that could form without it. After the dip is completed, the transformer is placed into an oven, and is baked until the varnish is dry. The main purpose of the varnish, besides increasing the electrical insulation, is to keep any form of moisture from affecting the coil, and to stop the windings from humming or vibrating when magnetized.
Wire selection[edit | edit source]
The wire generally used in small transformer coils is magnet wire. Magnet wire is generally a solid copper wire with an insulating jacket such as varnish. Other wires such as litz wire are common use for r.f. transformers. Large power transformers use stranded wire, which may be rectangular in cross-section, with periodic transpositions in the strands to equalize current and reduce loss. Windings for large currents may be made in strip form, or have a square or rectangular cross section. Aluminum is sometimes used in power transformer windings to reduce costs. The connections on smaller transformers are soldered, but larger transformer connections, especially ones handling high current, are brazed or welded.
The wire is selected by its ability to carry the proper amount of current without getting hot enough to melt the insulation or wire itself. It is sized by its cross sectional area measured in circular mils per ampere (CGS measurement system), or more commonly in engineering design circles, amperes per square meter (MKS measurement system). In transformer use, the circular mils per ampere runs anywhere from 500 cir. mils for intermittent operation, to 1500 cir. mils for heavy duty continuous operation. For most applications, 800 to 1000 cir. mils is a good starting point. The real value chosen is iterative, because heat is often not the limiting factor, as the desired regulation often puts the temperature rise well below insulation limits. Most wire charts have the wires cross sectional area in circular mils to make selection easier.


The core stack[edit | edit source]



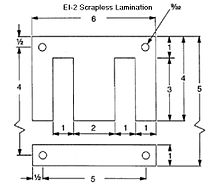
The core stack is the total amount of the steel laminations needed to produce the correct core area for the power in watts, or volt amperes that the transformer is required to handle.
The core can be stacked in two different ways when using steel laminations. The most common is the interleaved fashion where each lamination is staggered opposite to the other (turned 180 degrees opposite the other). This provides for the least amount of air gap in the core, and the highest efficiency. The other way is butt stacked. In this way, all the E type lams are stacked on one side, and all the I type lams are stacked on the other. This way though creates an air gap where the butt joint is created thus increasing the losses. However, when a DC current is superimposed on an AC current as in an audio transformer or filter choke, the air gap can stop the core from saturating. A combination of the two stacking types can be used with good results obtaining the best properties of both.
Stacking Factor[edit | edit source]
When using the formulas on this page to calculate the core area, a stacking factor should be included. The stacking factor is given by the lamination manufacturer on the individual specification sheet for each size lamination. It varies by the thickness of the material, type, and whether it is either butt stacked, or interleaved. This factor ranges from around 0.80 to 0.98. The formulas here can be used as is, but one will have a slightly smaller core if the factor is not added.
The stacking factor is needed due to each iron lamination having a thin coating of insulation on each face. This coating thereby insulates each lamination from the other minimizing eddy currents. The stacking factor adjusts the core size due to the extra thickness of this insulative coating so that the proper amount of iron is used in the core. Without this factor placed into the equations, the core would be slightly under-sized in iron content, even though the core stack equaled the calculated measurement. The core in mention, not using the stacking factor, would then have a slightly higher flux density than what was wanted. It is the ratio of sum of pure steel length to the designed length of laminated core.
Scrapless Laminations[edit | edit source]
When EI and other laminations are produced, they are literally punched out of a coiled strip of electrical steel with a punch press. To reduce the amount of scrap as much as possible, the lamination is dimensioned in such a way that if one placed two E laminations with their open ends toward each other, the two sections that make the windows would make the two I's needed when all four pieces are punched out at once. Due to this, the window width, and the leg width is generally 1/2 the width of the tongue. The window height would be equal to 1/2 the width of the whole E lamination. The lamination height would be equal to the window height plus the width of the window or leg. There are exceptions to this rule, as a few shapes have wider or taller windows such as custom laminations. These measurements are handy to know, as once one knows the tongue width, they will know the window width by dividing the tongue width in half. One could simply work out the total dimensions of a lamination in their mind when design time comes.
Core Stack Assembly[edit | edit source]
There are several ways that the core stack is held together after assembly. One way, is using mechanical fasteners, but this can promote a problem, if the fastener is made of a magnetic material, and the screw hole in the lamination is too far into the flux path of the lamination. If the magnetic flux cuts through a magnetic fastener, it causes the fastener to heat up, acting like a short-circuit, which in reality, is what happens, allowing the flux lines to mingle between the laminations as if they were shorted together. To cure this, the fastener holes in the laminations are generally placed in the far corner of the laminations, where the least amount of magnetic flux travels. Also, magnetic fasteners have been used by adding a paper sleeve over the screw, to insulate it somewhat, or a non-magnetic fastener, such as made from Aluminum or Brass, have been used.
Some transformers, today, have a welded seam placed on the outside of the laminations to hold them together, but this can cause a small amount of loss, the same way a magnetic screw would allow the magnetic flux to mingle between the insulated laminations. Since it is on the outside surface of the lamination, though, and away from the majority of the magnetic flux toward the center and coil, the loss is generally low.
Small power transformer are sometimes held together with a formed sheet metal housing, which encapsulates the circumference of the core stack, and this stops the need for using mechanical fasteners to hold the cores laminations together.
Watts versus volt-amperes[edit | edit source]
A transformer's power handling ability is determined in two different ways. If the transformer's secondary is supplying a totally resistive load, one can simply use wattage, or the voltage multiplied by the current. However, if the transformer's secondary is supplying a reactive load, containing capacitance and or inductance, such as in most DC power supplies, one must use volt-amperes in place of watts. Volt-amperes, (S) or (VA), is simply the RMS voltage times the RMS current, or, equivalently, wattage (P), divided by a power factor, or P / PF = VA; for example: 1000 watts (P) / 0.80 (PF) = 1,250 Volt-amperes (VA). The power factor for the better transformer circuits is around 0.80 to 0.85. However, some are lower, with a PF of around 0.60, especially in some appliance transformers.
When calculating the power required in Volt Amperes for the secondary windings in DC power supplies, one must take into account the equivalent series resistance of the capacitors, and or the way they, or any inductors act in the filtering circuits. This is due to the current either leading or lagging the voltage in reactive circuits, and or any harmonics. The type of rectifier circuit also comes into play, and is described in the following section. Also, please see this section for the formulae for the power, in volt amperes, of each rectifier circuit.
Rectifier transformers[edit | edit source]
Rectifier transformers are transformers used to feed a rectifier circuit which converts an AC current into a DC current. Due to the small conduction angle when feeding a rectifier & reservoir (capacitor), the rms AC current in the transformers secondary is somewhat higher than the DC load current. Each rectifier circuit has different conduction angles, and thus different rms current needs. The proper rms current the transformer needs to supply, and the volt amperes of each secondary, are calculated using the following formulae. (Note: Some may use "S" in place of "VA" in the following formulae). The formulae below does not take into consideration any extra current needed by voltage regulation circuits fed by the rectifier/filter assembly. They need to be added to the total power that the rectifier circuit will feed. Each rectifier and voltage regulation system uses different amounts of current, and each case has to be calculated differently.[4][5][6]
Half Wave Rectifier (HWR):
Without capacitor;
IAC = 1.6 x IDC
VA = 3.5 x (watts + IDC)
With capacitor;
IAC = 2.6 x IDC
VA = 2.3 x (watts + IDC)
Full Wave Center Tap (FWCT):
Without capacitor;
IAC = 0.8 x IDC
VA = 1.4 x (watts + IDC)
With capacitor;
IAC = 1.27 x IDC
VA = 1.7 x (watts + IDC)
Full Wave Bridge (FWB):
Without capacitor;
IAC = 1.1 x IDC
VA = 1.2 x (watts + (2 x IDC))
With capacitor;
IAC = 1.8 x IDC
VA = 1.4 x (watts + (2 x IDC))
Dual Complementary Rectifiers (DCR):
Without capacitor;
IAC = 1.1 x IDC
VA = 1.2 x (watts + (2 x IDC))
With capacitor;
IAC = 1.8 x IDC
VA = 1.4 x (watts + (2 x IDC))
Equations[edit | edit source]
There are two approaches used in designing transformers. One uses the long formulas, and the other uses the Wa product. The Wa product is simply the cores window area multiplied by the cores area. Some say it simplifies the design, especially in C-core (cut core) construction. Most manufacturers of C-cores have the Wa product added into the tables used in their selection. The designer takes the area used by a coil and finds a C-core with a similar window area. The Wa product is then divided by the window area to find the area of the core. Either way will bring the same result.
For a transformer designed for use with a sine wave, the universal voltage formula is:Ref:[7][8][9][10][11]
This gives way to the following other transformer equations for cores in square centimeters (cgs meas. sys.):
where,
- E is the sinusoidal rms or root mean square voltage of the winding,
- f is the frequency in hertz,
- N is the number of turns of wire on the winding,
- a is the cross-sectional area of the core in square centimeters or inches,
- B is the peak magnetic flux density in gauss (volt seconds per square centimeter), or lines (maxwells) per square inch ,
- P is the power in volt amperes or watts,
- W is the window area in square centimeters or inches and,
- J is the current density.
- Note: 10 kilogauss = 1 Tesla.
The derivation of the above formula is actually quite simple. The maximum induced voltage, , is the result of N times the time-varying flux:
If using RMS voltage values and E equal the rms value of voltage then:
and
Since the flux is created by a sinusoidal voltage, it too varies sinusoidally:
where = area of the core
Taking the derivative we have:
Substituting into the above equation and using and the fact that we are only concerned with the maximum value yields
Imperial measurement system[edit | edit source]
The formulas for the imperial (inch) system are still being used in the United States by many transformer manufacturers. Most steel EI laminations used in the US are measured in inches. The flux is still measured in gauss or Teslas, but the core area is measured in square inches. 28.638 is the conversion factor from 6.45 x 4.44 (see note 1) the 6.45 factor is simply the square of 2.54 cm in 1 Inch. The formulas for sine wave operation are below. For square wave operation, see Note (3):
To determine the power (P) capability of the core, the core stack in inches (D), and the window-area (Wa) product, the formulas are:
where,
- P is the power in volt amperes or watts,
- T is the number of turns per volt,
- E is the RMS voltage,
- S is the current density in circular mils per ampere (Generally 750 to 1500 cir mils),
- W is the window area in square inches,
- C is the core width in square inches,
- D is the depth of the stack in inches and,
- Wa is the product of the window area in square inches multiplied by the core area in square inches. This is especially useful for determining C-cores, but can also be used with EI types. The window area is simply the windows height multiplied by its width.
Simpler formulae[edit | edit source]
A shorter formula for the core area (a) and the turns per volt (T) can be derived from the long voltage formula by multiplying, rearranging, and dividing out. This is used if one wants to design a transformer using a sine wave, at a fixed flux density, and frequency. Below is the short formulas for core areas in square inches having a flux density of 12 kilogauss at 60 Hz (see note 2):
And for 12 kilogauss at 50 Hz:
Equation notes[edit | edit source]
- Note 1: The factor of 4.44 is derived from the first part of the voltage formula. It is from 4 multiplied by the form factor (F) which is 1.11, thus 4 multiplied by 1.11 = 4.44. The number 1.11 is derived from dividing the rms value of a sine wave by its average value, where F = rms / average = 1.11.
- Note 2: A value of 12 kilogauss per square inch (77,400 lines per sq. in.) is used for the short formulas above as it will work with most steel types used (M-2 to M-27), including unknown steel from scrap transformer laminations in TV sets, radios, and power supplies. The very lowest classes of steel (M-50) would probably not work as it should be run at or around 10 kilogauss or under.
- Note 3: All formulas shown are for sine wave operation only. Square wave operation does not use the form factor (F) of 1.11. For using square waves, substitute 4 for 4.44, and 25.8 for 28.638.
- Note 4: None of the above equations show the stacking factor (Sf). Each core or lamination will have its own stacking factor. It is selected by the size of the core or lamination, and the material it is made from. At design time, this is simply added to the string to be multiplied. Example; E = 4.44 f N a B Sf
Electrical steel types[edit | edit source]
Silicon steel[edit | edit source]
Iron was used in the first transformers and motor designs along with early steel. Steel is simply a de-carbonized alloy of iron. This early steel had the problem of aging, and it's magnetic properties changed with age. Next, silicon steel came into use, as it was found to raise the magnetic resistance against eddy currents, reduce hysteresis, increase permeability, and the aging problems were countered. Electrical silicon steel and its alloys are what are in use today. Ref:[12][13][14][15][16][17]
| Material | Type See Note (1) | Nominal Silicon % | Approx. Permeability μ (3) | Max. Recommended Operating Flux Density B | Usage |
| M-4, M-5, M-6 | CRGO | 2.8-3.5 | 15,000 | 17 kilogauss but magnetizing current rises rapidly over 15 kilogauss | Highest efficiency power transformers |
| M-7, M-8 | CRGO | 2.8-3.5 | 10,000 | 17 kilogauss but magnetizing current rises rapidly over 15 kilogauss | Large generators and power transformers |
| M-14 | CRNO | 4.0-5.0 | 8,500 | 14 kilogauss | Power and distribution transformers, high eff. rotating machines |
| M-15 | CRNO | 2.8-5.0 | 8,000 | 13 to 14 kilogauss | Transformers requiring low core loss and excellent permeability |
| M-19 | CRNO | 2.5-3.8 | 7,500 | 12 to 13 kilogauss | Communication transformers and reactors |
| M-22 | CRNO | 2.5-3.5 | 7,500 | 12 kilogauss | Cores of high reactance, intermittent duty transformers |
| M-27 | CRNO | 1.7-3.0 | 7,000 | 10 to 11 kilogauss | Small transformers operating at moderate induction |
| M-36 | CRNO | 1.4-2.2 | <7,000 | 10 kilogauss | Used extensively for rotating machines |
| M-43 | CRNO | 0.6-1.3 | <7,000 | 10 kilogauss | Fractional HP motors and relays |
| M-45 | CRNO | 0.0-0.6 | <7,000 | 10 kilogauss | Fractional HP motors and relays |
| M-50 | CRNO | 0.0-0.6 | <7,000 | 10 kilogauss | Intermittent operating apparatus and pole pieces |
- Note 1: CRGO = Cold rolled, grain oriented, and CRNO = cold rolled, non oriented.
- Note 2: In the "M" numberining system set by the ASTM, the smaller number yields the highest efficiency, and lowest core losses. M-43 has a core loss at 12 kilogauss of approx. 2 watts per pound. M-15 at 12 kilogauss is approx. 0.75 watts per pound, and M-6 material has a loss of 0.64 watts per pound at 15 kilogauss.[18][19]
- Note 3: These figures are relative permeability, (or are the permeability for a given material at a given flux density), and are unitless. For the actual permeability, multiply by the permeability of a vacuum μ0 in appropriate units. However, the Material Permeability, μm, of different materials can range from: Iron alloys, 0.8K to 25K, Ferrites, 0.8K to 20K, and Amorphous, 0.8K to 80K.Ref:[20]
- Note 4: For selection purposes, Armco (AK Steel), suggests the following for transformers in their non-oriented bulletin; Transformers over 10 KVA: M-15, M-19, and M-22. Transformers under 10 KVA: M-27, M-36, and M-43, however, M-19 has been used in certain smaller electronic amplifier transformers (0.5 KVA and up to 3 KVA). [21]
Other alloys[edit | edit source]
There are various iron alloys other than silicon-steel or low-carbon steel. These include alloys which contain nickel-iron (Permalloy), cobalt-nickel-iron (Perminvar), cobalt-iron (Permendur), and vanadium-cobalt-iron. Others include Supermalloy, amorphous Metglas, Mu-metal, Sendust, iron powder, and ferrite types.
Some of the Permalloy types are processed to accentuate the squareness of the B-H loop and carry proprietary names like SuperSquare 80 (Magnetic Metals Corp.), and Square Permalloy Hy-Ra 80 (Carpenter Steel Co.). The squareness of the B-H loop helps in switching transformers as in inverter type power supplies with a square wave input. The nickel-iron content may range from about 45% to over 85%.
Perminvar exhibits a substantially constant permeability and low hysteresis loss at low flux densities. This is mainly due to the addition of cobalt to the nickel and iron. In some cases it may have the odd property of low coercive force and remanence although the hysteresis loop area is still greater than zero. One type of Perminvar is Fernico.
Permendur is created by mixing cobalt with iron. It has a high permeability at high flux densities with a very high saturation point. It also has a high incremental permeability and is very good to use with a combination of AC and DC voltages combined such as in filter chokes.
Vanadium-cobalt-iron has the very highest saturation point with low losses, but it is very expensive.
For descriptions of the other materials and shapes, refer to the Wikipedia section titled Magnetic core.
DC Transformers[edit | edit source]


Transformers used in DC (Direct Current) circuits, generally consist of switching transformers in inverter type power supplies. These are widely used to convert 12 VDC to 115-120 VAC. However, the waveform produced is either a square wave, or a modified square wave. A modified square wave, is in reality, an attempt to create something similar to a sine wave, and it has a stair-step look on an oscilloscope. It is created by an electronic circuit that controls and steps the voltage level of the switching semiconductors output throughout one cycle.
The first switching power supplies, or "inverters", were controlled by a Vibrator that worked similar to an electric buzzer, and were used in the old tube type automobile radios. The Vibrator was merely a reed relay, with two sets of contacts, whose armature would switch back and forth at around 115 to 250 Hz, and create a square to flat-topped triangle wave output. It switched the positive and negative primary connections polarity back and forth at approximately 115-120 Hz. This fast switching speed allowed a smaller transformer core to be used, which was needed in the small radios of the time. It should be noted that the US Air Force adopted 400 Hz as the operating frequency for their power supplies to lighten the weight in aircraft. Now, higher frequencies are used to get away from the audible range, as switching transformers in the lower frequency range can produce a high-pitched noise from vibration. The higher frequencies keep the noise aspect down.
When semiconductors came into being, large PNP type Germanium transistors were used, like the 2N1522, and their bases were connected to a "tickler" winding on the transformer, which was out of phase with the primary, and supplied around 5 VAC (Square Wave) for bias. The tickler winding would set up the oscillation of the circuit, and relied on core saturation to work. The transistors then took the place of the vibrator, and created a square wave input to the primary of the transformer; some ran at higher frequencies. Since the transformer relied on saturation, a core with an interleaved stack was used. In some instances, toroidal transformers were used, made by winding a continuous strip of electrical steel into a dough-nut shape. The transformers coil was then wound over the toroid using a special winding machine.
Now, the switching is accomplished by both bipolar transistors and FETs (Field Effect Transistors). They are controlled either by an oscillator circuit, or an integrated circuit similar to a flip-flop, or multivibrator, such as in switched mode power supplies and flyback type transformer circuits. There are numerous switching circuits in use today. Transformer cores used with external oscillators, in this fashion, would be butt stacked, or a combination of butt and interleaving, or of the gapped ferrite type, due to the DC current within the windings. In this case, core saturation is not generally needed.
Transformers used at these higher frequencies are different from the larger 60 Hz line transformers, in that the core is constructed with thinner laminations. This is due to the losses because of Eddy currents, etc. at these frequencies, and the core material is made to suit the service. Higher frequency switch mode transformers, and flyback type transformers used to power the CRTs in computer monitors, use a ferrite type molded core.
However, in designing transformers for these square wave circuits, the above formulae are still used, except the form factor of 1.11, which is only used for sine waves, is not.




Impedance matching transformers[edit | edit source]


Impedance matching transformers are known by other names such as RF transformers, audio, and modulation transformers. Their function is to match one impedance in ohms to another.
Audio and modulation transformers generally have an electrical steel laminated core, but the material is thinner, and sometimes chemically different than line transformers. This is due to the higher frequency at which they are run. The core is designed around the lowest frequency and open circuit load, and at high frequencies around leakage inductance and winding capacitance. The primary may be wound with a two-piece primary with the first section against the core, the secondary on top of that, and the last half of the primary on the outside of the coil. Some air gap should be used in the core due to the DC current superimposed on the AC current.
RF (Radio Frequency) transformers are used between different stages of transistor or tube amplifiers in radio or transmitter circuits, or the impedance from the final amplifier to the load. Again, they match the primary impedance in ohms to the secondary impedance. The core is generally a form of Ferrite. Ferrite is made from a powdered iron oxide, with other alloys such as nickel oxide. Ferrite is used only in high to radio frequency circuits. The RF transformer is generally shielded with an enclosure made of copper or aluminum to shield it from interference from other radio signals. The core can be adjustable, using a threaded slug of ferrite, or it can be a core made up of ferrite toroids. There are also air core RF transformers used in push-pull RF amplifiers, and in matching networks.
For the formulae for the above, reference Wikipedia article: Impedance matching
.
References[edit | edit source]
- ↑ Humphries Jr., Stanley (2010). Finite-element Methods For Electromagnetics, PDF form of Field Solutions on Computers. ISBN 0-8493-1668-5
- ↑ Bossche & Valchev (2005). Inductors and Transformers for Power Electronics. ISBN 1-57444-679-7
- ↑ Winders Jr.,John J. (2002). Power Transformers, Principles and Applications. ISBN 0-8247-0766-4
- ↑ MCI, Basic Power Supply Application Quide
- ↑ Powertronix, Linear Power Supplies
- ↑ PowerVolt, How To Determine Power Supply Transformer Ratings
- ↑ McLyman,Col. William T. (1981). Transformer and Inductor Design Handbook. ISBN 978-0-824-75393-1
- ↑ Lowdon,Eric (1981). Practical Transformer Design Handbook. ISBN 978-0-672-21657-2
- ↑ Eng. Staff of Massachusetts Institute of Technology (1949). Magnetic Circuits and Transformers. John Wiley & Sons. ISBN 978-0-262-63063-4
- ↑ *The J&P Transformer Book, Heathcote, Martin (2007), ISBN 978-0-7506-8164-3
- ↑ *Hipersil Core Design Engineer's Handbook Westinghouse (1965)
- ↑ Lowdon,Eric (1981). Practical Transformer Design Handbook. ISBN 978-0-672-21657-2
- ↑ Fink,Donald (1969). Standard Handbook For Electrical Engineers. ISBN 978-0-070-22005-8
- ↑ McPherson,W (1981). Reference Data For Radio Engineers. ISBN 978-0-672-21218-5
- ↑ Eng. Staff of Massachusetts Institute of Technology (1949). Magnetic Circuits and Transformers. John Wiley & Sons. ISBN 978-0-262-63063-4
- ↑ *The J&P Transformer Book, Heathcote, Martin (2007), ISBN 978-0-7506-8164-3
- ↑ *Hipersil Core Design Engineer's Handbook Westinghouse (1965)
- ↑ Fink, Donald (1969). Standard Handbook For Electrical Engineers. ISBN 978-0-070-22005-8
- ↑ Eng. Staff of Massachusetts Institute of Technology (1949). Magnetic Circuits and Transformers. John Wiley & Sons. ISBN 978-0-262-63063-4
- ↑ McLyman,Col. William T. (1981). Transformer and Inductor Design Handbook.
- ↑ AK Steel, Nonoriented M-15 — M-47 Electrical Steel Bulletin (PDF)
- Practical Transformer Design Handbook, Lowdon, Eric (1981), ISBN 978-0-672-21657-2
- Standard Handbook For Electrical Engineers, Fink, Donald (1969), ISBN 978-0-070-22005-8
- Reference Data For Radio Engineers, McPherson, W (1981), ISBN 978-0-672-21218-5
- Magnetic Circuits and Transformers, Engineering Staff, MIT (1949), John Wiley & Sons. ISBN 978-0-262-63063-4
- The J&P Transformer Book, Heathcote, Martin (2007), ISBN 978-0-7506-8164-3
- Hipersil Core Design Engineer's Handbook, Westinghouse (1965)
- Transformer and Inductor Design Handbook, McLyman,Col. William T. (1981), ISBN 978-0-824-75393-1
- Finite-element Methods For Electromagnetics, PDF form of Field Solutions on Computers, Humphries Jr., Stanley (2010), ISBN 0-8493-1668-5
- Power Transformers, Principals and Applications, Winders Jr.,John J. (2002), ISBN 0-8247-0766-4
External links[edit | edit source]
- Ferrosilicon - Wikipedia
- Electrical steel - Wikipedia
- Magnetic core - Wikipedia
- Transformer - Wikipedia
- Electromagnetism - Wikipedia
- Ferrite core - Wikipedia
- Switched mode power supply - Wikipedia
- Flyback transformer - Wikipedia
Online book links[edit | edit source]
- Electronic Transformers and Circuits, Reuben Lee, Creative Commons License
- Hipersil Core Design Engineers Handbook, Westinghouse (1965), Creative Commons License

























