Discrete Mathematics/Set theory/Answers
Jump to navigation
Jump to search

Answers to Set Theory Exercise 1[edit | edit source]
1
- (a) Yes; alphanumeric characters are A…Z, a…z and 0…9
- (b) No; 'tall' is not well-defined
- (c) Yes; the set is {12.5}
- (d) Yes; the empty set
- (e) No; 'good' is not well-defined
2
- (a) T
- (b) F
- (c) T
- (d) F; A is a subset of U (which we meet in the next section)
- (e) F; {even numbers} means the set of all the even numbers, not just those between 2 and 10
3
- (a) {4, 33, √9}
- (b) {4, -5, 33, √9}
- (c) {4, 2/3, -2.5, -5, 33, √9}
- (d) {√2, π}
4
- (a) F
- (b) T
- (c) F
- (d) T
5 Examples might include:
- (a) {London, Paris, Rome, …}
- (b) {1, 3, 5, 7, …}, but not –3 or –1
- (c) {5, -5}
- (d) {3, 27, 243, …}
Back to Set Theory Exercise 1
Answers to Set Theory Exercise 2[edit | edit source]
1
| In A? | In B? | In C? | Region |
|---|---|---|---|
| Y | Y | Y | vi |
| Y | Y | N | iii |
| Y | N | Y | v |
| Y | N | N | ii |
| N | Y | Y | vii |
| N | Y | N | iv |
| N | N | Y | viii |
| N | N | N | i |
2
- They are all equal.
3
- (a) True (b) False (c) True
4
- (b) P ⊂ Q; R ⊂Q
- (c) False
5
Back to Set Theory Exercise 2
Answers to Set Theory Exercise 3[edit | edit source]
1
| (a) | (b) |
 |
A ∩ B = {6, 8}
A ∪ C = {2, 3, 4, 6, 7, 8, 10} A ′ = {1, 3, 5, 7, 9} B ′ = {2, 4, 5, 9, 10} B ∩ A ′ = {1, 3, 7} B ∩ C ′ = {1, 6, 8} A – B = {2, 4, 10} A Δ B = {1, 2, 3, 4, 7, 10} |
- (c)
- C - B = ø
2
- (a) F
- (b) F
- (c) T
3
- (a) P ⊆ Q
- (b) Q ⊆ P
4
| (a) | (b) |
 |
 |
| (c) | (d) |
 |
 |
| (e) | (f) |
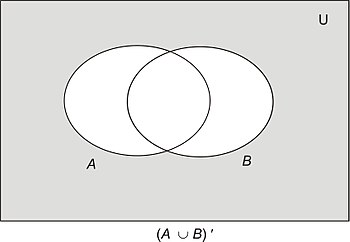 |
 |
5
- (a) B ′
- (b) A ∩ B ′
- (c) (A ∪ B) ∩ (A ∩ B) ′ or (A ∩ B ′) ∪ (A ′ ∩ B)
- (d) (A ∩ B) ∪ (A ′ ∩ B ′) or (A ∪ B) ′ ∪ (A ∩ B) or …?
6
- (a) Region (b) represents A – B. So A – B = A ∩ B ′
- (b) Region (c) represents A Δ B.
- So A Δ B = (A ∩ B) ∪ (A ′ ∩ B ′) or (A ∪ B) ′ ∪ (A ∩ B)
Back to Set Theory Exercise 3
Answers to Set Theory Exercise 4[edit | edit source]
1
- (a) P(A) = {ø, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2,4}, {3, 4}, {2, 3, 4}, {1, 3, 4}, {1, 2, 4}, {1, 2, 3}, {1, 2, 3, 4}}
- | P(A) | = 16
- (b) 32
- (c) 210 = 1024
2
| Law Used | ||||
| (a) | B ∪ (ø ∩ A) | = B ∪ (A ∩ ø) | Commutative | |
| = B ∪ ø | Identity | |||
| = B | Identity | |||
| (b) | (A ' ∩ U) ' | = (A' ) ' ∪ U' | De Morgan | |
| = A ∪ U' | Involution | |||
| = A ∪ ø | Complement | |||
| = A | Identity | |||
| (c) | (C ∪ A) ∩ (B ∪ A) | = (A ∪ C) ∩ (B ∪ A) | Commutative | |
| = (A ∪ C) ∩ (A ∪ B) | Commutative | |||
| = ((A ∪ C) ∩ B) ∪ ((A ∪ C) ∩ A) | Distributive | |||
| = ((A ∩ B) ∪ (C ∩ B)) ∪ (A ∪ (C ∩ A)) | Distributive | |||
| = ((B ∩ C) ∪ (A ∩ B)) ∪ (A ∪ (A ∩ C)) | Commutative (2x) | |||
| = ((B ∩ C) ∪ (A ∩ B)) ∪ ((A ∩ U) ∪ (A ∩ C)) | Identity | |||
| = ((B ∩ C) ∪ (A ∩ B)) ∪ (A ∩ (U ∪ C)) | Distributive | |||
| = ((B ∩ C) ∪ (A ∩ B)) ∪ (A ∩ U) | Identity | |||
| = ((B ∩ C) ∪ (A ∩ B)) ∪ A | Identity | |||
| = (B ∩ C) ∪ ((A ∩ B) ∪ A)) | Associative | |||
| = (B ∩ C) ∪ ((A ∩ B) ∪ (A ∩ U)) | Identity | |||
| = (B ∩ C) ∪ (A ∩ (B ∪ U)) | Distributive | |||
| = (B ∩ C) ∪ (A ∩ U) | Identity | |||
| = (B ∩ C) ∪ A | Identity | |||
| = A ∪ (B ∩ C) | Commutative | |||
| (d) | (A ∩ B) ∪ (A ∩ B ' ) | = A ∩ (B ∪ B ' ) | Distributive | |
| = A ∩ U | Complement | |||
| = A | Identity | |||
| (e) | (A ∩ B) ∪ (A ∪ B ' ) ' | = (A ∩ B) ∪ (A ' ∩ (B ' ) ' ) | De Morgan | |
| = (A ∩ B) ∪ (A ' ∩ B) | Involution | |||
| = (B ∩ A) ∪ (B ∩ A ' ) | Commutative (× 2) | |||
| = B ∩ (A ∪ A ' ) | Distributive | |||
| = B ∩ U | Complement | |||
| = B | Identity | |||
| (f) | A ∩ (A ∪ B) | = (A ∪ ø) ∩ (A ∪ B) | Identity | |
| = A ∪ (ø ∩ B) | Distributive | |||
| = A ∩ (B ∩ ø) | Commutative | |||
| = A ∪ ø | Identity | |||
| = A | Identity |
Back to Set Theory Exercise 4
Answers to Set Theory Exercise 5[edit | edit source]
1
- (a) X × Y = {(a, a), (a, b), (a, e), (a, f), (c, a), (c, b), (c, e), (c, f)}
- (b) Y × X = {(a, a), (a, c), (b, a), (b, c), (e, a), (e, c), (f, a), (f, c)}
- (c) X × X = {(a, a), (a, c), (c, a), (c, c)}
- (d) They are equal: A = B
2
- (a) (b, 2), (b, 4), (c, 1), (c, 5), (e, 1), (e, 5), (f, 2), (f, 4)
- (b) P = C × R
- (c) ((G × R) ∪ (C × T)) - (G × T)
3
- V = {pqr | (p, q, r) ∈ L × (L ∪ D) × (L ∪ D)}
4

- The shaded area is the same in each case, so it looks as though the proposition is true.
Back to Set Theory Exercise 5




