Control Systems/Modern Controls/Print version
| This is the print version of Control Systems/Modern Controls You won't see this message or any elements not part of the book's content when you print or preview this page. |
The Wikibook of automatic
And Control Systems Engineering
With
Classical and Modern Techniques
And
Advanced Concepts
Introduction to Control Systems
What are control systems? Why do we study them? How do we identify them? The chapters in this section should answer these questions and more.
Introduction
This Wikibook
This book was written at Wikibooks, a free online community where people write open-content textbooks. Any person with internet access is welcome to participate in the creation and improvement of this book. Because this book is continuously evolving, there are no finite "versions" or "editions" of this book. Permanent links to known good versions of the pages may be provided.
What are Control Systems?
The study and design of automatic Control Systems, a field known as control engineering, has become important in modern technical society. From devices as simple as a toaster or a toilet, to complex machines like space shuttles and power steering, control engineering is a part of our everyday life. This book introduces the field of control engineering and explores some of the more advanced topics in the field. Note, however, that control engineering is a very large field and this book serves only as a foundation of control engineering and an introduction to selected advanced topics in the field. Topics in this book are added at the discretion of the authors and represent the available expertise of our contributors.
Control systems are components that are added to other components to increase functionality or meet a set of design criteria. For example:
We have a particular electric motor that is supposed to turn at a rate of 40 RPM. To achieve this speed, we must supply 10 Volts to the motor terminals. However, with 10 volts supplied to the motor at rest, it takes 30 seconds for our motor to get up to speed. This is valuable time lost.
This simple example can be complex to both users and designers of the motor system. It may seem obvious that the motor should start at a higher voltage so that it accelerates faster. Then we can reduce the supply back down to 10 volts once it reaches ideal speed.
This is clearly a simplistic example but it illustrates an important point: we can add special "Controller units" to preexisting systems to improve performance and meet new system specifications.
Here are some formal definitions of terms used throughout this book:
- Control System
- A Control System is a device, or a collection of devices that manage the behavior of other devices. Some devices are not controllable. A control system is an interconnection of components connected or related in such a manner as to command, direct, or regulate itself or another system.
Control System is a conceptual framework for designing systems with capabilities of regulation and/or tracking to give a desired performance. For this there must be a set of signals measurable to know the performance, another set of signals measurable to influence the evolution of the system in time and a third set which is not measurable but disturb the evolution.
- Controller
- A controller is a control system that manages the behavior of another device or system (using Actuators). The controller is usually fed with some input signal from outside the system which commands the system to provide desired output. In a closed loop system, the signal is preprocessed with the sensor's signal from inside the system.
- Actuator
- An actuator is a device that takes in a signal form the controller and carries some action to affect the system accordingly.
- Compensator
- A compensator is a control system that regulates another system, usually by conditioning the input or the output to that system. Compensators are typically employed to correct a single design flaw with the intention of minimizing effects on other aspects of the design.
There are essentially two methods to approach the problem of designing a new control system: the Classical Approach and the Modern Approach.
Classical and Modern
Classical and Modern control methodologies are named in a misleading way, because the group of techniques called "Classical" were actually developed later than the techniques labeled "Modern". However, in terms of developing control systems, Modern methods have been used to great effect more recently, while the Classical methods have been gradually falling out of favor. Most recently, it has been shown that Classical and Modern methods can be combined to highlight their respective strengths and weaknesses.
Classical Methods, which this book will consider first, are methods involving the Laplace Transform domain. Physical systems are modeled in the so-called "time domain", where the response of a given system is a function of the various inputs, the previous system values, and time. As time progresses, the state of the system and its response change. However, time-domain models for systems are frequently modeled using high-order differential equations which can become impossibly difficult for humans to solve and some of which can even become impossible for modern computer systems to solve efficiently. To counteract this problem, integral transforms, such as the Laplace Transform and the Fourier Transform, can be employed to change an Ordinary Differential Equation (ODE) in the time domain into a regular algebraic polynomial in the transform domain. Once a given system has been converted into the transform domain it can be manipulated with greater ease and analyzed quickly by humans and computers alike.
Modern Control Methods, instead of changing domains to avoid the complexities of time-domain ODE mathematics, converts the differential equations into a system of lower-order time domain equations called State Equations, which can then be manipulated using techniques from linear algebra. This book will consider Modern Methods second.
A third distinction that is frequently made in the realm of control systems is to divide analog methods (classical and modern, described above) from digital methods. Digital Control Methods were designed to try and incorporate the emerging power of computer systems into previous control methodologies. A special transform, known as the Z-Transform, was developed that can adequately describe digital systems, but at the same time can be converted (with some effort) into the Laplace domain. Once in the Laplace domain, the digital system can be manipulated and analyzed in a very similar manner to Classical analog systems. For this reason, this book will not make a hard and fast distinction between Analog and Digital systems, and instead will attempt to study both paradigms in parallel.
Who is This Book For?
This book is intended to accompany a course of study in under-graduate and graduate engineering. As has been mentioned previously, this book is not focused on any particular discipline within engineering, however any person who wants to make use of this material should have some basic background in the Laplace transform (if not other transforms), calculus, etc. The material in this book may be used to accompany several semesters of study, depending on the program of your particular college or university. The study of control systems is generally a topic that is reserved for students in their 3rd or 4th year of a 4 year undergraduate program, because it requires so much previous information. Some of the more advanced topics may not be covered until later in a graduate program.
Many colleges and universities only offer one or two classes specifically about control systems at the undergraduate level. Some universities, however, do offer more than that, depending on how the material is broken up, and how much depth that is to be covered. Also, many institutions will offer a handful of graduate-level courses on the subject. This book will attempt to cover the topic of control systems from both a graduate and undergraduate level, with the advanced topics built on the basic topics in a way that is intuitive. As such, students should be able to begin reading this book in any place that seems an appropriate starting point, and should be able to finish reading where further information is no longer needed.
What are the Prerequisites?
Understanding of the material in this book will require a solid mathematical foundation. This book does not currently explain, nor will it ever try to fully explain most of the necessary mathematical tools used in this text. For that reason, the reader is expected to have read the following wikibooks, or have background knowledge comparable to them:
- Algebra
- Calculus
- The reader should have a good understanding of differentiation and integration. Partial differentiation, multiple integration, and functions of multiple variables will be used occasionally, but the students are not necessarily required to know those subjects well. These advanced calculus topics could better be treated as a co-requisite instead of a pre-requisite.
- Linear Algebra
- State-space system representation draws heavily on linear algebra techniques. Students should know how to operate on matrices. Students should understand basic matrix operations (addition, multiplication, determinant, inverse, transpose). Students would also benefit from a prior understanding of Eigenvalues and Eigenvectors, but those subjects are covered in this text.
- Ordinary Differential Equations
- All linear systems can be described by a linear ordinary differential equation. It is beneficial, therefore, for students to understand these equations. Much of this book describes methods to analyze these equations. Students should know what a differential equation is, and they should also know how to find the general solutions of first and second order ODEs.
- Engineering Analysis
- This book reinforces many of the advanced mathematical concepts used in the Engineering Analysis book, and we will refer to the relevant sections in the aforementioned text for further information on some subjects. This is essentially a math book, but with a focus on various engineering applications. It relies on a previous knowledge of the other math books in this list.
- Signals and Systems
- The Signals and Systems book will provide a basis in the field of systems theory, of which control systems is a subset. Readers who have not read the Signals and Systems book will be at a severe disadvantage when reading this book.
How is this Book Organized?
This book will be organized following a particular progression. First this book will discuss the basics of system theory, and it will offer a brief refresher on integral transforms. Section 2 will contain a brief primer on digital information, for students who are not necessarily familiar with them. This is done so that digital and analog signals can be considered in parallel throughout the rest of the book. Next, this book will introduce the state-space method of system description and control. After section 3, topics in the book will use state-space and transform methods interchangeably (and occasionally simultaneously). It is important, therefore, that these three chapters be well read and understood before venturing into the later parts of the book.
After the "basic" sections of the book, we will delve into specific methods of analyzing and designing control systems. First we will discuss Laplace-domain stability analysis techniques (Routh-Hurwitz, root-locus), and then frequency methods (Nyquist Criteria, Bode Plots). After the classical methods are discussed, this book will then discuss Modern methods of stability analysis. Finally, a number of advanced topics will be touched upon, depending on the knowledge level of the various contributors.
As the subject matter of this book expands, so too will the prerequisites. For instance, when this book is expanded to cover nonlinear systems, a basic background knowledge of nonlinear mathematics will be required.
Versions
This wikibook has been expanded to include multiple versions of its text, differentiated by the material covered, and the order in which the material is presented. Each different version is composed of the chapters of this book, included in a different order. This book covers a wide range of information, so if you don't need all the information that this book has to offer, perhaps one of the other versions would be right for you and your educational needs.
Each separate version has a table of contents outlining the different chapters that are included in that version. Also, each separate version comes complete with a printable version, and some even come with PDF versions as well.
Take a look at the All Versions Listing Page to find the version of the book that is right for you and your needs.
Differential Equations Review
Implicit in the study of control systems is the underlying use of differential equations. Even if they aren't visible on the surface, all of the continuous-time systems that we will be looking at are described in the time domain by ordinary differential equations (ODE), some of which are relatively high-order.
Let's review some differential equation basics. Consider the topic of interest from a bank. The amount of interest accrued on a given principal balance (the amount of money you put into the bank) P, is given by:
Where is the interest (rate of change of the principal), and r is the interest rate. Notice in this case that P is a function of time (t), and can be rewritten to reflect that:
To solve this basic, first-order equation, we can use a technique called "separation of variables", where we move all instances of the letter P to one side, and all instances of t to the other:
And integrating both sides gives us:
This is all fine and good, but generally, we like to get rid of the logarithm, by raising both sides to a power of e:
Where we can separate out the constant as such:
D is a constant that represents the initial conditions of the system, in this case the starting principal.
Differential equations are particularly difficult to manipulate, especially once we get to higher-orders of equations. Luckily, several methods of abstraction have been created that allow us to work with ODEs, but at the same time, not have to worry about the complexities of them. The classical method, as described above, uses the Laplace, Fourier, and Z Transforms to convert ODEs in the time domain into polynomials in a complex domain. These complex polynomials are significantly easier to solve than the ODE counterparts. The Modern method instead breaks differential equations into systems of low-order equations, and expresses this system in terms of matrices. It is a common precept in ODE theory that an ODE of order N can be broken down into N equations of order 1.
Readers who are unfamiliar with differential equations might be able to read and understand the material in this book reasonably well. However, all readers are encouraged to read the related sections in Calculus.
History
The field of control systems started essentially in the ancient world. Early civilizations, notably the Greeks and the Arabs were heavily preoccupied with the accurate measurement of time, the result of which were several "water clocks" that were designed and implemented.
However, there was very little in the way of actual progress made in the field of engineering until the beginning of the renaissance in Europe. Leonhard Euler (for whom Euler's Formula is named) discovered a powerful integral transform, but Pierre-Simon Laplace used the transform (later called the Laplace Transform) to solve complex problems in probability theory.
Joseph Fourier was a court mathematician in France under Napoleon I. He created a special function decomposition called the Fourier Series, that was later generalized into an integral transform, and named in his honor (the Fourier Transform).

|

|
| Pierre-Simon Laplace 1749-1827 |
Joseph Fourier 1768-1840 |
The "golden age" of control engineering occurred between 1910-1945, where mass communication methods were being created and two world wars were being fought. During this period, some of the most famous names in controls engineering were doing their work: Nyquist and Bode.
Hendrik Wade Bode and Harry Nyquist, especially in the 1930's while working with Bell Laboratories, created the bulk of what we now call "Classical Control Methods". These methods were based off the results of the Laplace and Fourier Transforms, which had been previously known, but were made popular by Oliver Heaviside around the turn of the century. Previous to Heaviside, the transforms were not widely used, nor respected mathematical tools.
Bode is credited with the "discovery" of the closed-loop feedback system, and the logarithmic plotting technique that still bears his name (bode plots). Harry Nyquist did extensive research in the field of system stability and information theory. He created a powerful stability criteria that has been named for him (The Nyquist Criteria).
Modern control methods were introduced in the early 1950's, as a way to bypass some of the shortcomings of the classical methods. Rudolf Kalman is famous for his work in modern control theory, and an adaptive controller called the Kalman Filter was named in his honor. Modern control methods became increasingly popular after 1957 with the invention of the computer, and the start of the space program. Computers created the need for digital control methodologies, and the space program required the creation of some "advanced" control techniques, such as "optimal control", "robust control", and "nonlinear control". These last subjects, and several more, are still active areas of study among research engineers.
Branches of Control Engineering
Here we are going to give a brief listing of the various different methodologies within the sphere of control engineering. Oftentimes, the lines between these methodologies are blurred, or even erased completely.
- Classical Controls
- Control methodologies where the ODEs that describe a system are transformed using the Laplace, Fourier, or Z Transforms, and manipulated in the transform domain.
- Modern Controls
- Methods where high-order differential equations are broken into a system of first-order equations. The input, output, and internal states of the system are described by vectors called "state variables".
- Robust Control
- Control methodologies where arbitrary outside noise/disturbances are accounted for, as well as internal inaccuracies caused by the heat of the system itself, and the environment.
- Optimal Control
- In a system, performance metrics are identified, and arranged into a "cost function". The cost function is minimized to create an operational system with the lowest cost.
- Adaptive Control
- In adaptive control, the control changes its response characteristics over time to better control the system.
- Nonlinear Control
- The youngest branch of control engineering, nonlinear control encompasses systems that cannot be described by linear equations or ODEs, and for which there is often very little supporting theory available.
- Game Theory
- Game Theory is a close relative of control theory, and especially robust control and optimal control theories. In game theory, the external disturbances are not considered to be random noise processes, but instead are considered to be "opponents". Each player has a cost function that they attempt to minimize, and that their opponents attempt to maximize.
This book will definitely cover the first two branches, and will hopefully be expanded to cover some of the later branches, if time allows.
MATLAB
the Appendix
MATLAB ® is a programming tool that is commonly used in the field of control engineering. We will discuss MATLAB in specific sections of this book devoted to that purpose. MATLAB will not appear in discussions outside these specific sections, although MATLAB may be used in some example problems. An overview of the use of MATLAB in control engineering can be found in the appendix at: Control Systems/MATLAB.
For more information on MATLAB in general, see: MATLAB Programming.
Resources
Nearly all textbooks on the subject of control systems, linear systems, and system analysis will use MATLAB as an integral part of the text. Students who are learning this subject at an accredited university will certainly have seen this material in their textbooks, and are likely to have had MATLAB work as part of their classes. It is from this perspective that the MATLAB appendix is written.
In the future, this book may be expanded to include information on Simulink ®, as well as MATLAB.
There are a number of other software tools that are useful in the analysis and design of control systems. Additional information can be added in the appendix of this book, depending on the experience and prior knowledge of contributors.
About Formatting
This book will use some simple conventions throughout.
Mathematical Conventions
Mathematical equations will be labeled with the {{eqn}} template, to give them names. Equations that are labeled in such a manner are important, and should be taken special note of. For instance, notice the label to the right of this equation:
[Inverse Laplace Transform]
Equations that are named in this manner will also be copied into the List of Equations Glossary in the end of the book, for an easy reference.
Italics will be used for English variables, functions, and equations that appear in the main text. For example e, j, f(t) and X(s) are all italicized. Wikibooks contains a LaTeX mathematics formatting engine, although an attempt will be made not to employ formatted mathematical equations inline with other text because of the difference in size and font. Greek letters, and other non-English characters will not be italicized in the text unless they appear in the midst of multiple variables which are italicized (as a convenience to the editor).
Scalar time-domain functions and variables will be denoted with lower-case letters, along with a t in parenthesis, such as: x(t), y(t), and h(t). Discrete-time functions will be written in a similar manner, except with an [n] instead of a (t).
Fourier, Laplace, Z, and Star transformed functions will be denoted with capital letters followed by the appropriate variable in parenthesis. For example: F(s), X(jω), Y(z), and F*(s).
Matrices will be denoted with capital letters. Matrices which are functions of time will be denoted with a capital letter followed by a t in parenthesis. For example: A(t) is a matrix, a(t) is a scalar function of time.
Transforms of time-variant matrices will be displayed in uppercase bold letters, such as H(s).
Math equations rendered using LaTeX will appear on separate lines, and will be indented from the rest of the text.
Text Conventions
Examples will appear in TextBox templates, which show up as large grey boxes filled with text and equations.
- Important Definitions
- Will appear in TextBox templates as well, except we will use this formatting to show that it is a definition.
Notes of interest will appear in "infobox" templates. These notes will often be used to explain some nuances of a mathematical derivation or proof. |
Warnings will appear in these "warning" boxes. These boxes will point out common mistakes, or other items to be careful of. |
System Identification
Systems
Systems, in one sense, are devices that take input and produce an output. A system can be thought to operate on the input to produce the output. The output is related to the input by a certain relationship known as the system response. The system response usually can be modeled with a mathematical relationship between the system input and the system output.
System Properties
Physical systems can be divided up into a number of different categories, depending on particular properties that the system exhibits. Some of these system classifications are very easy to work with and have a large theory base for analysis. Some system classifications are very complex and have still not been investigated with any degree of success. By properly identifying the properties of a system, certain analysis and design tools can be selected for use with the system.
The early sections of this book will focus primarily on linear time-invariant (LTI) systems. LTI systems are the easiest class of system to work with, and have a number of properties that make them ideal to study. This chapter discusses some properties of systems.
Later chapters in this book will look at time variant systems and nonlinear systems. Both time variant and nonlinear systems are very complex areas of current research, and both can be difficult to analyze properly. Unfortunately, most physical real-world systems are time-variant, nonlinear, or both.
An introduction to system identification and least squares techniques can be found here. An introduction to parameter identification techniques can be found here.
Initial Time
The initial time of a system is the time before which there is no input. Typically, the initial time of a system is defined to be zero, which will simplify the analysis significantly. Some techniques, such as the Laplace Transform require that the initial time of the system be zero. The initial time of a system is typically denoted by t0.
The value of any variable at the initial time t0 will be denoted with a 0 subscript. For instance, the value of variable x at time t0 is given by:
Likewise, any time t with a positive subscript are points in time after t0, in ascending order:
So t1 occurs after t0, and t2 occurs after both points. In a similar fashion above, a variable with a positive subscript (unless specifying an index into a vector) also occurs at that point in time:
This is valid for all points in time t.
Additivity
A system satisfies the property of additivity if a sum of inputs results in a sum of outputs. By definition: an input of results in an output of . To determine whether a system is additive, use the following test:
Given a system f that takes an input x and outputs a value y, assume two inputs (x1 and x2) produce two outputs:
Now, create a composite input that is the sum of the previous inputs:
Then the system is additive if the following equation is true:
Systems that satisfy this property are called additive. Additive systems are useful because a sum of simple inputs can be used to analyze the system response to a more complex input.
Example: Sinusoids
Given the following equation:
Create a sum of inputs as:
and construct the expected sum of outputs:
Now, substituting these values into our equation, test for equality:
The equality is not satisfied, and therefore the sine operation is not additive.
Homogeneity
A system satisfies the condition of homogeneity if an input scaled by a certain factor produces an output scaled by that same factor. By definition: an input of results in an output of . In other words, to see if function f() is homogeneous, perform the following test:
Stimulate the system f with an arbitrary input x to produce an output y:
Now, create a second input x1, scale it by a multiplicative factor C (C is an arbitrary constant value), and produce a corresponding output y1:
Now, assign x to be equal to x1:
Then, for the system to be homogeneous, the following equation must be true:
Systems that are homogeneous are useful in many applications, especially applications with gain or amplification.
Example: Straight-Line
Given the equation for a straight line:
Comparing the two results, it is easy to see they are not equal:
Therefore, the equation is not homogeneous.
Exercise:
Prove that additivity implies homogeneity, but that homogeneity does not imply additivity.
Linearity
A system is considered linear if it satisfies the conditions of Additivity and Homogeneity. In short, a system is linear if the following is true:
Take two arbitrary inputs, and produce two arbitrary outputs:
Now, a linear combination of the inputs should produce a linear combination of the outputs:
This condition of additivity and homogeneity is called superposition. A system is linear if it satisfies the condition of superposition.
Example: Linear Differential Equations
Is the following equation linear:
To determine whether this system is linear, construct a new composite input:
Now, create the expected composite output:
Substituting the two into our original equation:
Factor out the derivative operator, as such:
Finally, convert the various composite terms into the respective variables, to prove that this system is linear:
For the record, derivatives and integrals are linear operators, and ordinary differential equations typically are linear equations.
Memory
A system is said to have memory if the output from the system is dependent on past inputs (or future inputs!) to the system. A system is called memoryless if the output is only dependent on the current input. Memoryless systems are easier to work with, but systems with memory are more common in digital signal processing applications.
Systems that have memory are called dynamic systems, and systems that do not have memory are static systems.
Causality
Causality is a property that is very similar to memory. A system is called causal if it is only dependent on past and/or current inputs. A system is called anti-causal if the output of the system is dependent only on future inputs. A system is called non-causal if the output depends on past and/or current and future inputs.
A system design that is not causal cannot be physically implemented (to operate in a real-time). If the system can't be built, the design is generally worthless. However, there are applications of non-causal systems, e.g. when a system does not need to operate in a real-time and already has signals stored in its memory (sound and image compression). |
Time-Invariance
A system is called time-invariant if the system relationship between the input and output signals is not dependent on the passage of time. If the input signal produces an output then any time shifted input, , results in a time-shifted output This property can be satisfied if the transfer function of the system is not a function of time except expressed by the input and output. If a system is time-invariant then the system block is commutative with an arbitrary delay. This facet of time-invariant systems will be discussed later.
To determine if a system f is time-invariant, perform the following test:
Apply an arbitrary input x to a system and produce an arbitrary output y:
Apply a second input x1 to the system, and produce a second output:
Now, assign x1 to be equal to the first input x, time-shifted by a given constant value δ:
Finally, a system is time-invariant if y1 is equal to y shifted by the same value δ:
LTI Systems
A system is considered to be a Linear Time-Invariant (LTI) system if it satisfies the requirements of time-invariance and linearity. LTI systems are one of the most important types of systems, and they will be considered almost exclusively in the beginning chapters of this book.
Systems which are not LTI are more common in practice, but are much more difficult to analyze.
Lumpedness
A system is said to be lumped if one of the two following conditions are satisfied:
- There are a finite number of states that the system can be in.
- There are a finite number of state variables.
The concept of "states" and "state variables" are relatively advanced, and they will be discussed in more detail in the discussion about modern controls.
Systems which are not lumped are called distributed. A simple example of a distributed system is a system with delay, that is, , which has an infinite number of state variables (Here we use to denote the Laplace variable). However, although distributed systems are quite common, they are very difficult to analyze in practice, and there are few tools available to work with such systems. Fortunately, in most cases, a delay can be sufficiently modeled with the Pade approximation. This book will not discuss distributed systems much.
Relaxed
A system is said to be relaxed if the system is causal and at the initial time t0 the output of the system is zero, i.e., there is no stored energy in the system. The output is excited solely and uniquely by input applied thereafter.
In terms of differential equations, a relaxed system is said to have "zero initial states". Systems without an initial state are easier to work with, but systems that are not relaxed can frequently be modified to approximate relaxed systems.
Stability
Stability is a very important concept in systems, but it is also one of the hardest function properties to prove. There are several different criteria for system stability, but the most common requirement is that the system must produce a finite output when subjected to a finite input. For instance, if 5 volts is applied to the input terminals of a given circuit, it would be best if the circuit output didn't approach infinity, and the circuit itself didn't melt or explode. This type of stability is often known as "Bounded Input, Bounded Output" stability, or BIBO.
There are a number of other types of stability, most of which are based on the concept of BIBO stability. Because stability is such an important and complicated topic, an entire section of this text is devoted to its study.
Inputs and Outputs
Systems can also be categorized by the number of inputs and the number of outputs the system has. Consider a television as a system, for instance. The system has two inputs: the power wire and the signal cable. It has one output: the video display. A system with one input and one output is called single-input, single output, or SISO. a system with multiple inputs and multiple outputs is called multi-input, multi-output, or MIMO.
These systems will be discussed in more detail later.
Exercise:
Based on the definitions of SISO and MIMO, above, determine what the acronyms SIMO and MISO mean.
Digital and Analog
Digital and Analog
There is a significant distinction between an analog system and a digital system, in the same way that there is a significant difference between analog and digital data. This book is going to consider both analog and digital topics, so it is worth taking some time to discuss the differences, and to display the different notations that will be used with each.
Continuous Time
A signal is called continuous-time if it is defined at every time t.
A system is a continuous-time system if it takes a continuous-time input signal, and outputs a continuous-time output signal. Here is an example of an analog waveform:

Discrete Time
A signal is called discrete-time if it is only defined for particular points in time. A discrete-time system takes discrete-time input signals, and produces discrete-time output signals. The following image shows the difference between an analog waveform and the sampled discrete time equivalent:

Quantized
A signal is called Quantized if it can only be certain values, and cannot be other values. This concept is best illustrated with examples:
- Students with a strong background in physics will recognize this concept as being the root word in "Quantum Mechanics". In quantum mechanics, it is known that energy comes only in discrete packets. An electron bound to an atom, for example, may occupy one of several discrete energy levels, but not intermediate levels.
- Another common example is population statistics. For instance, a common statistic is that a household in a particular country may have an average of "3.5 children", or some other fractional number. Actual households may have 3 children, or they may have 4 children, but no household has 3.5 children.
- People with a computer science background will recognize that integer variables are quantized because they can only hold certain integer values, not fractions or decimal points.
The last example concerning computers is the most relevant, because quantized systems are frequently computer-based. Systems that are implemented with computer software and hardware will typically be quantized.
Here is an example waveform of a quantized signal. Notice how the magnitude of the wave can only take certain values, and that creates a step-like appearance. This image is discrete in magnitude, but is continuous in time:

Analog
By definition:
- Analog
- A signal is considered analog if it is defined for all points in time and if it can take any real magnitude value within its range.
An analog system is a system that represents data using a direct conversion from one form to another. In other words, an analog system is a system that is continuous in both time and magnitude.
Example: Motor
If we have a given motor, we can show that the output of the motor (rotation in units of radians per second, for instance) is a function of the voltage that is input to the motor. We can show the relationship as such:
Where is the output in terms of rad/sec, and is the motor's conversion function between the input voltage () and the output. For any value of we can calculate out specifically what the rotational speed of the motor should be.
Example: Analog Clock
Consider a standard analog clock, which represents the passage of time though the angular position of the clock hands. We can denote the angular position of the hands of the clock with the system of equations:
Where is the angular position of the hour hand, is the angular position of the minute hand, and is the angular position of the second hand. The positions of all the different hands of the clock are dependent on functions of time.
Different positions on a clock face correspond directly to different times of the day.
Digital
Digital data is represented by discrete number values. By definition:
- Digital
- A signal or system is considered digital if it is both discrete-time and quantized.
Digital data always have a certain granularity, and therefore there will almost always be an error associated with using such data, especially if we want to account for all real numbers. The tradeoff, of course, to using a digital system is that our powerful computers with our powerful, Moore's law microprocessor units, can be instructed to operate on digital data only. This benefit more than makes up for the shortcomings of a digital representation system.
Discrete systems will be denoted inside square brackets, as is a common notation in texts that deal with discrete values. For instance, we can denote a discrete data set of ascending numbers, starting at 1, with the following notation:
- x[n] = [1 2 3 4 5 6 ...]
n, or other letters from the central area of the alphabet (m, i, j, k, l, for instance) are commonly used to denote discrete time values. Analog, or "non-discrete" values are denoted in regular expression syntax, using parenthesis. Here is an example of an analog waveform and the digital equivalent. Notice that the digital waveform is discrete in both time and magnitude:
 |
 |
Example: Digital Clock
As a common example, let's consider a digital clock: The digital clock represents time with binary electrical data signals of 1 and 0. The 1's are usually represented by a positive voltage, and a 0 is generally represented by zero voltage. Counting in binary, we can show that any given time can be represented by a base-2 numbering system:
Minute Binary Representation 1 1 10 1010 30 11110 59 111011
But what happens if we want to display a fraction of a minute, or a fraction of a second? A typical digital clock has a certain amount of precision, and it cannot express fractional values smaller than that precision.
Hybrid Systems
Hybrid Systems are systems that have both analog and digital components. Devices called samplers are used to convert analog signals into digital signals, and Devices called reconstructors are used to convert digital signals into analog signals. Because of the use of samplers, hybrid systems are frequently called sampled-data systems.
Example: Automobile Computer
Most modern automobiles today have integrated computer systems that monitor certain aspects of the car, and actually help to control the performance of the car. The speed of the car, and the rotational speed of the transmission are analog values, but a sampler converts them into digital values so the car computer can monitor them. The digital computer will then output control signals to other parts of the car, to alter analog systems such as the engine timing, the suspension, the brakes, and other parts. Because the car has both digital and analog components, it is a hybrid system.
Continuous and Discrete
We are not using the word "continuous" here in the sense of continuously differentiable, as is common in math texts.
A system is considered continuous-time if the signal exists for all time. Frequently, the terms "analog" and "continuous" will be used interchangeably, although they are not strictly the same.
Discrete systems can come in three flavors:
- Discrete time (sampled)
- Discrete magnitude (quantized)
- Discrete time and magnitude (digital)
Discrete magnitude systems are systems where the signal value can only have certain values.Discrete time systems are systems where signals are only available (or valid) at particular times. Computer systems are discrete in the sense of (3), in that data is only read at specific discrete time intervals, and the data can have only a limited number of discrete values.
A discrete-time system has a sampling time value associated with it, such that each discrete value occurs at multiples of the given sampling time. We will denote the sampling time of a system as T. We can equate the square-brackets notation of a system with the continuous definition of the system as follows:
Notice that the two notations show the same thing, but the first one is typically easier to write, and it shows that the system in question is a discrete system. This book will use the square brackets to denote discrete systems by the sample number n, and parenthesis to denote continuous time functions.
Sampling and Reconstruction
The process of converting analog information into digital data is called "Sampling". The process of converting digital data into an analog signal is called "Reconstruction". We will talk about both processes in a later chapter. For more information on the topic than is available in this book, see the Analog and Digital Conversion wikibook. Here is an example of a reconstructed waveform. Notice that the reconstructed waveform here is quantized because it is constructed from a digital signal:

System Metrics
System Metrics
When a system is being designed and analyzed, it doesn't make any sense to test the system with all manner of strange input functions, or to measure all sorts of arbitrary performance metrics. Instead, it is in everybody's best interest to test the system with a set of standard, simple reference functions. Once the system is tested with the reference functions, there are a number of different metrics that we can use to determine the system performance.
It is worth noting that the metrics presented in this chapter represent only a small number of possible metrics that can be used to evaluate a given system. This wikibook will present other useful metrics along the way, as their need becomes apparent.
Standard Inputs
All of the standard inputs are zero before time zero. All the standard inputs are causal.
There are a number of standard inputs that are considered simple enough and universal enough that they are considered when designing a system. These inputs are known as a unit step, a ramp, and a parabolic input.
- Unit Step
- A unit step function is defined piecewise as such:
[Unit Step Function]
- The unit step function is a highly important function, not only in control systems engineering, but also in signal processing, systems analysis, and all branches of engineering. If the unit step function is input to a system, the output of the system is known as the step response. The step response of a system is an important tool, and we will study step responses in detail in later chapters.

- Ramp
- A unit ramp is defined in terms of the unit step function, as such:
[Unit Ramp Function]
- It is important to note that the unit step function is simply the differential of the unit ramp function:
- This definition will come in handy when we learn about the Laplace Transform.

- Parabolic
- A unit parabolic input is similar to a ramp input:
[Unit Parabolic Function]
- Notice also that the unit parabolic input is equal to the integral of the ramp function:
- Again, this result will become important when we learn about the Laplace Transform.
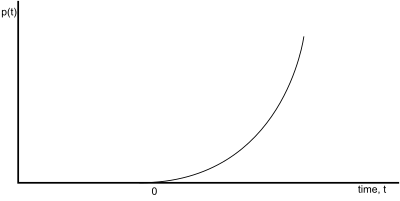
Also, sinusoidal and exponential functions are considered basic, but they are too difficult to use in initial analysis of a system.
Steady State
To be more precise, we should have taken the limit as t approaches infinity. However, as a shorthand notation, we will typically say "t equals infinity", and assume the reader understands the shortcut that is being used.
When a unit-step function is input to a system, the steady-state value of that system is the output value at time . Since it is impractical (if not completely impossible) to wait till infinity to observe the system, approximations and mathematical calculations are used to determine the steady-state value of the system. Most system responses are asymptotic, that is that the response approaches a particular value. Systems that are asymptotic are typically obvious from viewing the graph of that response.
Step Response
The step response of a system is most frequently used to analyze systems, and there is a large amount of terminology involved with step responses. When exposed to the step input, the system will initially have an undesirable output period known as the transient response. The transient response occurs because a system is approaching its final output value. The steady-state response of the system is the response after the transient response has ended.
The amount of time it takes for the system output to reach the desired value (before the transient response has ended, typically) is known as the rise time. The amount of time it takes for the transient response to end and the steady-state response to begin is known as the settling time.
It is common for a systems engineer to try and improve the step response of a system. In general, it is desired for the transient response to be reduced, the rise and settling times to be shorter, and the steady-state to approach a particular desired "reference" output.
 |
 |
Target Value
The target output value is the value that our system attempts to obtain for a given input. This is not the same as the steady-state value, which is the actual value that the system does obtain. The target value is frequently referred to as the reference value, or the "reference function" of the system. In essence, this is the value that we want the system to produce. When we input a "5" into an elevator, we want the output (the final position of the elevator) to be the fifth floor. Pressing the "5" button is the reference input, and is the expected value that we want to obtain. If we press the "5" button, and the elevator goes to the third floor, then our elevator is poorly designed.
Rise Time
Rise time is the amount of time that it takes for the system response to reach the target value from an initial state of zero. Many texts on the subject define the rise time as being the time it takes to rise between the initial position and 80% of the target value. This is because some systems never rise to 100% of the expected, target value, and therefore they would have an infinite rise-time. This book will specify which convention to use for each individual problem. Rise time is typically denoted tr, or trise.
Rise time is not the amount of time it takes to achieve steady-state, only the amount of time it takes to reach the desired target value for the first time. |
Percent Overshoot
Underdamped systems frequently overshoot their target value initially. This initial surge is known as the "overshoot value". The ratio of the amount of overshoot to the target steady-state value of the system is known as the percent overshoot. Percent overshoot represents an overcompensation of the system, and can output dangerously large output signals that can damage a system. Percent overshoot is typically denoted with the term PO.
Example: Refrigerator
Consider an ordinary household refrigerator. The refrigerator has cycles where it is on and when it is off. When the refrigerator is on, the coolant pump is running, and the temperature inside the refrigerator decreases. The temperature decreases to a much lower level than is required, and then the pump turns off.
When the pump is off, the temperature slowly increases again as heat is absorbed into the refrigerator. When the temperature gets high enough, the pump turns back on. Because the pump cools down the refrigerator more than it needs to initially, we can say that it "overshoots" the target value by a certain specified amount.
Example: Refrigerator
Another example concerning a refrigerator concerns the electrical demand of the heat pump when it first turns on. The pump is an inductive mechanical motor, and when the motor first activates, a special counter-acting force known as "back EMF" resists the motion of the motor, and causes the pump to draw more electricity until the motor reaches its final speed. During the startup time for the pump, lights on the same electrical circuit as the refrigerator may dim slightly, as electricity is drawn away from the lamps, and into the pump. This initial draw of electricity is a good example of overshoot.
Steady-State Error
Sometimes a system might never achieve the desired steady-state value, but instead will settle on an output value that is not desired. The difference between the steady-state output value to the reference input value at steady state is called the steady-state error of the system. We will use the variable ess to denote the steady-state error of the system.
Settling Time
After the initial rise time of the system, some systems will oscillate and vibrate for an amount of time before the system output settles on the final value. The amount of time it takes to reach steady state after the initial rise time is known as the settling time. Notice that damped oscillating systems may never settle completely, so we will define settling time as being the amount of time for the system to reach, and stay in, a certain acceptable range. The acceptable range for settling time is typically determined on a per-problem basis, although common values are 20%, 10%, or 5% of the target value. The settling time will be denoted as ts.
System Order
The order of the system is defined by the number of independent energy storage elements in the system, and intuitively by the highest order of the linear differential equation that describes the system. In a transfer function representation, the order is the highest exponent in the transfer function. In a proper system, the system order is defined as the degree of the denominator polynomial. In a state-space equation, the system order is the number of state-variables used in the system. The order of a system will frequently be denoted with an n or N, although these variables are also used for other purposes. This book will make clear distinction on the use of these variables.
Proper Systems
A proper system is a system where the degree of the denominator is larger than or equal to the degree of the numerator polynomial. A strictly proper system is a system where the degree of the denominator polynomial is larger than (but never equal to) the degree of the numerator polynomial. A biproper system is a system where the degree of the denominator polynomial equals the degree of the numerator polynomial.
It is important to note that only proper systems can be physically realized. In other words, a system that is not proper cannot be built. It makes no sense to spend a lot of time designing and analyzing imaginary systems.
Example: System Order
Find the order of this system:
The highest exponent in the denominator is s2, so the system is order 2. Also, since the denominator is a higher degree than the numerator, this system is strictly proper.
In the above example, G(s) is a second-order transfer function because in the denominator one of the s variables has an exponent of 2. Second-order functions are the easiest to work with.
System Type
Let's say that we have a process transfer function (or combination of functions, such as a controller feeding in to a process), all in the forward branch of a unity feedback loop. Say that the overall forward branch transfer function is in the following generalized form (known as pole-zero form):
[Pole-Zero Form]
we call the parameter M the system type. Note that increased system type number correspond to larger numbers of poles at s = 0. More poles at the origin generally have a beneficial effect on the system, but they increase the order of the system, and make it increasingly difficult to implement physically. System type will generally be denoted with a letter like N, M, or m. Because these variables are typically reused for other purposes, this book will make clear distinction when they are employed.
Now, we will define a few terms that are commonly used when discussing system type. These new terms are Position Error, Velocity Error, and Acceleration Error. These names are throwbacks to physics terms where acceleration is the derivative of velocity, and velocity is the derivative of position. Note that none of these terms are meant to deal with movement, however.
- Position Error
- The position error, denoted by the position error constant . This is the amount of steady-state error of the system when stimulated by a unit step input. We define the position error constant as follows:
[Position Error Constant]
- Where G(s) is the transfer function of our system.
- Velocity Error
- The velocity error is the amount of steady-state error when the system is stimulated with a ramp input. We define the velocity error constant as such:
[Velocity Error Constant]
- Acceleration Error
- The acceleration error is the amount of steady-state error when the system is stimulated with a parabolic input. We define the acceleration error constant to be:
[Acceleration Error Constant]
Now, this table will show briefly the relationship between the system type, the kind of input (step, ramp, parabolic), and the steady-state error of the system:
Unit System Input Type, M Au(t) Ar(t) Ap(t) 0 1 2 > 2
Z-Domain Type
Likewise, we can show that the system order can be found from the following generalized transfer function in the Z domain:
Where the constant M is the type of the digital system. Now, we will show how to find the various error constants in the Z-Domain:
[Z-Domain Error Constants]
Error Constant Equation Kp Kv Ka
Visually
Here is an image of the various system metrics, acting on a system in response to a step input:

The target value is the value of the input step response. The rise time is the time at which the waveform first reaches the target value. The overshoot is the amount by which the waveform exceeds the target value. The settling time is the time it takes for the system to settle into a particular bounded region. This bounded region is denoted with two short dotted lines above and below the target value.
System Modeling
The Control Process
It is the job of a control engineer to analyze existing systems, and to design new systems to meet specific needs. Sometimes new systems need to be designed, but more frequently a controller unit needs to be designed to improve the performance of existing systems. When designing a system, or implementing a controller to augment an existing system, we need to follow some basic steps:
- Model the system mathematically
- Analyze the mathematical model
- Design system/controller
- Implement system/controller and test
The vast majority of this book is going to be focused on (2), the analysis of the mathematical systems. This chapter alone will be devoted to a discussion of the mathematical modeling of the systems.
External Description
An external description of a system relates the system input to the system output without explicitly taking into account the internal workings of the system. The external description of a system is sometimes also referred to as the Input-Output Description of the system, because it only deals with the inputs and the outputs to the system.

If the system can be represented by a mathematical function h(t, r), where t is the time that the output is observed, and r is the time that the input is applied. We can relate the system function h(t, r) to the input x and the output y through the use of an integral:
[General System Description]
This integral form holds for all linear systems, and every linear system can be described by such an equation.
If a system is causal (i.e. an input at t=r affects system behaviour only for ) and there is no input of the system before t=0, we can change the limits of the integration:
Time-Invariant Systems
If furthermore a system is time-invariant, we can rewrite the system description equation as follows:
This equation is known as the convolution integral, and we will discuss it more in the next chapter.
Every Linear Time-Invariant (LTI) system can be used with the Laplace Transform, a powerful tool that allows us to convert an equation from the time domain into the S-Domain, where many calculations are easier. Time-variant systems cannot be used with the Laplace Transform.
Internal Description
If a system is linear and lumped, it can also be described using a system of equations known as state-space equations. In state-space equations, we use the variable x to represent the internal state of the system. We then use u as the system input, and we continue to use y as the system output. We can write the state-space equations as such:
We will discuss the state-space equations more when we get to the section on modern controls.
Complex Descriptions
Systems which are LTI and Lumped can also be described using a combination of the state-space equations, and the Laplace Transform. If we take the Laplace Transform of the state equations that we listed above, we can get a set of functions known as the Transfer Matrix Functions. We will discuss these functions in a later chapter.
Representations
To recap, we will prepare a table with the various system properties, and the available methods for describing the system:
Properties State-Space
EquationsLaplace
TransformTransfer
MatrixLinear, Time-Variant, Distributed no no no Linear, Time-Variant, Lumped yes no no Linear, Time-Invariant, Distributed no yes no Linear, Time-Invariant, Lumped yes yes yes
We will discuss all these different types of system representation later in the book.
Analysis
Once a system is modeled using one of the representations listed above, the system needs to be analyzed. We can determine the system metrics and then we can compare those metrics to our specification. If our system meets the specifications we are finished with the design process. However if the system does not meet the specifications (as is typically the case), then suitable controllers and compensators need to be designed and added to the system.
Once the controllers and compensators have been designed, the job isn't finished: we need to analyze the new composite system to ensure that the controllers work properly. Also, we need to ensure that the systems are stable: unstable systems can be dangerous.
Frequency Domain
For proposals, early stage designs, and quick turn around analyses a frequency domain model is often superior to a time domain model. Frequency domain models take disturbance PSDs (Power Spectral Densities) directly, use transfer functions directly, and produce output or residual PSDs directly. The answer is a steady-state response. Oftentimes the controller is shooting for 0 so the steady-state response is also the residual error that will be the analysis output or metric for report.
| Input | Model | Output |
|---|---|---|
| PSD | Transfer Function | PSD |
Brief Overview of the Math
Frequency domain modeling is a matter of determining the impulse response of a system to a random process.

where
- is the one-sided input PSD in
- is the frequency response function of the system and
- is the one-sided output PSD or auto power spectral density function.
The frequency response function, , is related to the impulse response function (transfer function) by
Note some texts will state that this is only valid for random processes which are stationary. Other texts suggest stationary and ergodic while still others state weakly stationary processes. Some texts do not distinguish between strictly stationary and weakly stationary. From practice, the rule of thumb is if the PSD of the input process is the same from hour to hour and day to day then the input PSD can be used and the above equation is valid.
Notes
- ↑ Sun, Jian-Qiao (2006). Stochastic Dynamics and Control, Volume 4. Amsterdam: Elsevier Science. ISBN 0444522301.
See a full explanation with example at ControlTheoryPro.com
Modeling Examples
Modeling in Control Systems is oftentimes a matter of judgement. This judgement is developed by creating models and learning from other people's models. ControlTheoryPro.com is a site with a lot of examples. Here are links to a few of them
- Hovering Helicopter Example
- Reaction Torque Cancellation Example
- List of all examples at ControlTheoryPro.com
Manufacture
Once the system has been properly designed we can prototype our system and test it. Assuming our analysis was correct and our design is good, the prototype should work as expected. Now we can move on to manufacture and distribute our completed systems.
Modern Controls
The modern method of controls uses systems of special state-space equations to model and manipulate systems. The state variable model is broad enough to be useful in describing a wide range of systems, including systems that cannot be adequately described using the Laplace Transform. These chapters will require the reader to have a solid background in linear algebra, and multi-variable calculus.
State-Space Equations
Time-Domain Approach
The "Classical" method of controls (what we have been studying so far) has been based mostly in the transform domain. When we want to control the system in general, we represent it using the Laplace transform (Z-Transform for digital systems) and when we want to examine the frequency characteristics of a system we use the Fourier Transform. The question arises, why do we do this?
Let's look at a basic second-order Laplace Transform transfer function:
We can decompose this equation in terms of the system inputs and outputs:
Now, when we take the inverse Laplace transform of our equation, we can see that:
The Laplace transform is transforming the fact that we are dealing with second-order differential equations. The Laplace transform moves a system out of the time-domain into the complex frequency domain so we can study and manipulate our systems as algebraic polynomials instead of linear ODEs. Given the complexity of differential equations, why would we ever want to work in the time domain?
It turns out that to decompose our higher-order differential equations into multiple first-order equations, one can find a new method for easily manipulating the system without having to use integral transforms. The solution to this problem is state variables . By taking our multiple first-order differential equations and analyzing them in vector form, we can not only do the same things we were doing in the time domain using simple matrix algebra, but now we can easily account for systems with multiple inputs and outputs without adding much unnecessary complexity. This demonstrates why the "modern" state-space approach to controls has become popular.
State-Space
In a state-space system, the internal state of the system is explicitly accounted for by an equation known as the state equation. The system output is given in terms of a combination of the current system state, and the current system input, through the output equation. These two equations form a system of equations known collectively as state-space equations. The state-space is the vector space that consists of all the possible internal states of the system.
For a system to be modeled using the state-space method, the system must meet this requirement:
- The system must be "lumped"
"Lumped" in this context, means that we can find a finite-dimensional state-space vector which fully characterises all such internal states of the system.
This text mostly considers linear state-space systems where the state and output equations satisfy the superposition principle. However, the state-space approach is equally valid for nonlinear systems although some specific methods are not applicable to nonlinear systems.
State
Central to the state-space notation is the idea of a state. A state of a system is the current value of internal elements of the system which change separately (but are not completely unrelated) to the output of the system. In essence, the state of a system is an explicit account of the values of the internal system components. Here are some examples:
Consider an electric circuit with both an input and an output terminal. This circuit may contain any number of inductors and capacitors. The state variables may represent the magnetic and electric fields of the inductors and capacitors, respectively.
Consider a spring-mass-dashpot system. The state variables may represent the compression of the spring, or the acceleration at the dashpot.
Consider a chemical reaction where certain reagents are poured into a mixing container, and the output is the amount of the chemical product produced over time. The state variables may represent the amounts of un-reacted chemicals in the container, or other properties such as the quantity of thermal energy in the container that can serve to facilitate the reaction.
State Variables
When modeling a system using a state-space equation, we first need to define three vectors:
- Input variables
- A SISO (Single-Input Single-Output) system will only have one input value, but a MIMO (Multiple-Input Multiple-Output) system may have multiple inputs. We need to define all the inputs to the system and arrange them into a vector.
- Output variables
- This is the system output value, and in the case of MIMO systems we may have several. Output variables should be independent of one another, and only dependent on a linear combination of the input vector and the state vector.
- State Variables
- The state variables represent values from inside the system that can change over time. In an electric circuit for instance, the node voltages or the mesh currents can be state variables. In a mechanical system, the forces applied by springs, gravity, and dashpots can be state variables.
We denote the input variables with u, the output variables with y, and the state variables with x. In essence, we have the following relationship:
Where f(x, u) is our system. Also, the state variables can change with respect to the current state and the system input:
Where x' is the rate of change of the state variables. We will define f(u, x) and g(u, x) in the next chapter.
Multi-Input, Multi-Output
In the Laplace domain, if we want to account for systems with multiple inputs and multiple outputs, we are going to need to rely on the principle of superposition to create a system of simultaneous Laplace equations for each input and output. For such systems, the classical approach not only doesn't simplify the situation, but because the systems of equations need to be transformed into the frequency domain first, manipulated, and then transformed back into the time domain, they can actually be more difficult to work with. However, the Laplace domain technique can be combined with the State-Space techniques discussed in the next few chapters to bring out the best features of both techniques. We will discuss MIMO systems in the MIMO Systems Chapter.
State-Space Equations
In a state-space system representation, we have a system of two equations: an equation for determining the state of the system, and another equation for determining the output of the system. We will use the variable y(t) as the output of the system, x(t) as the state of the system, and u(t) as the input of the system. We use the notation x'(t) (note the prime) for the first derivative of the state vector of the system, as dependent on the current state of the system and the current input. Symbolically, we say that there are transforms g and h, that display this relationship:
If x'(t) and y(t) are not linear combinations of x(t) and u(t), the system is said to be nonlinear. We will attempt to discuss non-linear systems in a later chapter.
The first equation shows that the system state change is dependent on the previous system state, the initial state of the system, the time, and the system inputs. The second equation shows that the system output is dependent on the current system state, the system input, and the current time.
If the system state change x'(t) and the system output y(t) are linear combinations of the system state and input vectors, then we can say the systems are linear systems, and we can rewrite them in matrix form:
[State Equation]
[Output Equation]
If the systems themselves are time-invariant, we can re-write this as follows:
The State Equation shows the relationship between the system's current state and its input, and the future state of the system. The Output Equation shows the relationship between the system state and its input, and the output. These equations show that in a given system, the current output is dependent on the current input and the current state. The future state is also dependent on the current state and the current input.
It is important to note at this point that the state space equations of a particular system are not unique, and there are an infinite number of ways to represent these equations by manipulating the A, B, C and D matrices using row operations. There are a number of "standard forms" for these matrices, however, that make certain computations easier. Converting between these forms will require knowledge of linear algebra.
- State-Space Basis Theorem
- Any system that can be described by a finite number of nth order differential equations or nth order difference equations, or any system that can be approximated by them, can be described using state-space equations. The general solutions to the state-space equations, therefore, are solutions to all such sets of equations.
Matrices: A B C D
Our system has the form:
We've bolded several quantities to try and reinforce the fact that they can be vectors, not just scalar quantities. If these systems are time-invariant, we can simplify them by removing the time variables:
Now, if we take the partial derivatives of these functions with respect to the input and the state vector at time t0, we get our system matrices:
In our time-invariant state space equations, we write these matrices and their relationships as:
We have four constant matrices: A, B, C, and D. We will explain these matrices below:
- Matrix A
- Matrix A is the system matrix, and relates how the current state affects the state change x' . If the state change is not dependent on the current state, A will be the zero matrix. The exponential of the state matrix, eAt is called the state transition matrix, and is an important function that we will describe below.
- Matrix B
- Matrix B is the control matrix, and determines how the system input affects the state change. If the state change is not dependent on the system input, then B will be the zero matrix.
- Matrix C
- Matrix C is the output matrix, and determines the relationship between the system state and the system output.
- Matrix D
- Matrix D is the feed-forward matrix, and allows for the system input to affect the system output directly. A basic feedback system like those we have previously considered do not have a feed-forward element, and therefore for most of the systems we have already considered, the D matrix is the zero matrix.
Matrix Dimensions
Because we are adding and multiplying multiple matrices and vectors together, we need to be absolutely certain that the matrices have compatible dimensions, or else the equations will be undefined. For integer values p, q, and r, the dimensions of the system matrices and vectors are defined as follows:
Vectors Matrices
Matrix Dimensions:
A: p × p
B: p × q
C: r × p
D: r × q
If the matrix and vector dimensions do not agree with one another, the equations are invalid and the results will be meaningless. Matrices and vectors must have compatible dimensions or they cannot be combined using matrix operations.
For the rest of the book, we will be using the small template on the right as a reminder about the matrix dimensions, so that we can keep a constant notation throughout the book.
Notational Shorthand
The state equations and the output equations of systems can be expressed in terms of matrices A, B, C, and D. Because the form of these equations is always the same, we can use an ordered quadruplet to denote a system. We can use the shorthand (A, B, C, D) to denote a complete state-space representation. Also, because the state equation is very important for our later analysis, we can write an ordered pair (A, B) to refer to the state equation:
Obtaining the State-Space Equations
The beauty of state equations, is that they can be used to transparently describe systems that are both continuous and discrete in nature. Some texts will differentiate notation between discrete and continuous cases, but this text will not make such a distinction. Instead we will opt to use the generic coefficient matrices A, B, C and D for both continuous and discrete systems. Occasionally this book may employ the subscript C to denote a continuous-time version of the matrix, and the subscript D to denote the discrete-time version of the same matrix. Other texts may use the letters F, H, and G for continuous systems and Γ, and Θ for use in discrete systems. However, if we keep track of our time-domain system, we don't need to worry about such notations.
From Differential Equations
Let's say that we have a general 3rd order differential equation in terms of input u(t) and output y(t):
We can create the state variable vector x in the following manner:
Which now leaves us with the following 3 first-order equations:
Now, we can define the state vector x in terms of the individual x components, and we can create the future state vector as well:
- ,
And with that, we can assemble the state-space equations for the system:
Granted, this is only a simple example, but the method should become apparent to most readers.
From Transfer Functions
The method of obtaining the state-space equations from the Laplace domain transfer functions are very similar to the method of obtaining them from the time-domain differential equations. We call the process of converting a system description from the Laplace domain to the state-space domain realization. We will discuss realization in more detail in a later chapter. In general, let's say that we have a transfer function of the form:
We can write our A, B, C, and D matrices as follows:
This form of the equations is known as the controllable canonical form of the system matrices, and we will discuss this later.
Notice that to perform this method, the denominator and numerator polynomials must be monic, the coefficients of the highest-order term must be 1. If the coefficient of the highest order term is not 1, you must divide your equation by that coefficient to make it 1.
State-Space Representation
As an important note, remember that the state variables x are user-defined and therefore are arbitrary. There are any number of ways to define x for a particular problem, each of which are going to lead to different state space equations.
Note: There are an infinite number of equivalent ways to represent a system using state-space equations. Some ways are better than others. Once these state-space equations are obtained, they can be manipulated to take a particular form if needed.
Consider the previous continuous-time example. We can rewrite the equation in the form
- .
We now define the state variables
with first-order derivatives
- (suspected error here. Fails to account that :. encapsulates : five lines earlier.)
The state-space equations for the system will then be given by
x may also be used in any number of variable transformations, as a matter of mathematical convenience. However, the variables y and u correspond to physical signals, and may not be arbitrarily selected, redefined, or transformed as x can be.
Example: Dummy Variables
The altitude control of a particular manned aircraft can be given by:
Where α is the direction the aircraft is traveling in, θ is the direction the aircraft is facing (the attitude), and δ is the angle of the ailerons (the control input from the pilot). This equation is not in a proper format, so we need to produce some dummy-variables:
This in turn will provide us with our state equation:
As we can see from this equation, even though we have a valid state-equation, the variables θ1 and θ2 don't necessarily correspond to any measurable physical event, but are instead dummy variables constructed by the user to help define the system. Note, however, that the variables α and δ do correspond to physical values, and cannot be changed.
Discretization
If we have a system (A, B, C, D) that is defined in continuous time, we can discretize the system so that an equivalent process can be performed using a digital computer. We can use the definition of the derivative, as such:
And substituting this into the state equation with some approximation (and ignoring the limit for now) gives us:
We are able to remove that limit because in a discrete system, the time interval between samples is positive and non-negligible. By definition, a discrete system is only defined at certain time points, and not at all time points as the limit would have indicated. In a discrete system, we are interested only in the value of the system at discrete points. If those points are evenly spaced by every T seconds (the sampling time), then the samples of the system occur at t = kT, where k is an integer. Substituting kT for t into our equation above gives us:
Or, using the square-bracket shorthand that we've developed earlier, we can write:
In this form, the state-space system can be implemented quite easily into a digital computer system using software, not complicated analog hardware. We will discuss this relationship and digital systems more specifically in a later chapter.
We will write out the discrete-time state-space equations as:
Note on Notations
The variable T is a common variable in control systems, especially when talking about the beginning and end points of a continuous-time system, or when discussing the sampling time of a digital system. However, another common use of the letter T is to signify the transpose operation on a matrix. To alleviate this ambiguity, we will denote the transpose of a matrix with a prime:
Where A' is the transpose of matrix A.
The prime notation is also frequently used to denote the time-derivative. Most of the matrices that we will be talking about are time-invariant; there is no ambiguity because we will never take the time derivative of a time-invariant matrix. However, for a time-variant matrix we will use the following notations to distinguish between the time-derivative and the transpose:
- the transpose.
- the time-derivative.
Note that certain variables which are time-variant are not written with the (t) postscript, such as the variables x, y, and u. For these variables, the default behavior of the prime is the time-derivative, such as in the state equation. If the transpose needs to be taken of one of these vectors, the (t)' postfix will be added explicitly to correspond to our notation above.
For instances where we need to use the Hermitian transpose, we will use the notation:
This notation is common in other literature, and raises no obvious ambiguities here.
MATLAB Representation
State-space systems can be represented in MATLAB using the 4 system matrices, A, B, C, and D. We can create a system data structure using the ss function:
sys = ss(A, B, C, D);
Systems created in this way can be manipulated in the same way that the transfer function descriptions (described earlier) can be manipulated. To convert a transfer function to a state-space representation, we can use the tf2ss function:
[A, B, C, D] = tf2ss(num, den);
And to perform the opposite operation, we can use the ss2tf function:
[num, den] = ss2tf(A, B, C, D);
Solutions for Linear Systems
State Equation Solutions
The state equation is a first-order linear differential equation, or (more precisely) a system of linear differential equations. Because this is a first-order equation, we can use results from Ordinary Differential Equations to find a general solution to the equation in terms of the state-variable x. Once the state equation has been solved for x, that solution can be plugged into the output equation. The resulting equation will show the direct relationship between the system input and the system output, without the need to account explicitly for the internal state of the system. The sections in this chapter will discuss the solutions to the state-space equations, starting with the easiest case (Time-invariant, no input), and ending with the most difficult case (Time-variant systems).
Solving for x(t) With Zero Input
Looking again at the state equation:
We can see that this equation is a first-order differential equation, except that the variables are vectors, and the coefficients are matrices. However, because of the rules of matrix calculus, these distinctions don't matter. We can ignore the input term (for now), and rewrite this equation in the following form:
And we can separate out the variables as such:
Integrating both sides, and raising both sides to a power of e, we obtain the result:
Where C is a constant. We can assign D = eC to make the equation easier, but we also know that D will then be the initial conditions of the system. This becomes obvious if we plug the value zero into the variable t. The final solution to this equation then is given as:
We call the matrix exponential eAt the state-transition matrix, and calculating it, while difficult at times, is crucial to analyzing and manipulating systems. We will talk more about calculating the matrix exponential below.
Solving for x(t) With Non-Zero Input
If, however, our input is non-zero (as is generally the case with any interesting system), our solution is a little bit more complicated. Notice that now that we have our input term in the equation, we will no longer be able to separate the variables and integrate both sides easily.
We subtract to get the on the left side, and then we do something curious; we premultiply both sides by the inverse state transition matrix:
The rationale for this last step may seem fuzzy at best, so we will illustrate the point with an example:
Example
Take the derivative of the following with respect to time:
The product rule from differentiation reminds us that if we have two functions multiplied together:
and we differentiate with respect to t, then the result is:
If we set our functions accordingly:
Then the output result is:
If we look at this result, it is the same as from our equation above.
Using the result from our example, we can condense the left side of our equation into a derivative:
Now we can integrate both sides, from the initial time (t0) to the current time (t), using a dummy variable τ, we will get closer to our result. Finally, if we premultiply by eAt, we get our final result:
[General State Equation Solution]
If we plug this solution into the output equation, we get:
[General Output Equation Solution]
This is the general Time-Invariant solution to the state space equations, with non-zero input. These equations are important results, and students who are interested in a further study of control systems would do well to memorize these equations.
State-Transition Matrix
Engineering Analysis
The state transition matrix, eAt, is an important part of the general state-space solutions for the time-invariant cases listed above. Calculating this matrix exponential function is one of the very first things that should be done when analyzing a new system, and the results of that calculation will tell important information about the system in question.
The matrix exponential can be calculated directly by using a Taylor-Series expansion:
Engineering Analysis
Also, we can attempt to diagonalize the matrix A into a diagonal matrix or a Jordan Canonical matrix. The exponential of a diagonal matrix is simply the diagonal elements individually raised to that exponential. The exponential of a Jordan canonical matrix is slightly more complicated, but there is a useful pattern that can be exploited to find the solution quickly. Interested readers should read the relevant passages in Engineering Analysis.
The state transition matrix, and matrix exponentials in general are very important tools in control engineering.
Diagonal Matrices
If a matrix is diagonal, the state transition matrix can be calculated by raising each diagonal entry of the matrix raised as a power of e.
Jordan Canonical Form
If the A matrix is in the Jordan Canonical form, then the matrix exponential can be generated quickly using the following formula:
Where λ is the eigenvalue (the value on the diagonal) of the jordan-canonical matrix.
Inverse Laplace Method
We can calculate the state-transition matrix (or any matrix exponential function) by taking the following inverse Laplace transform:
If A is a high-order matrix, this inverse can be difficult to solve.
If the A matrix is in the Jordan Canonical form, then the matrix exponential can be generated quickly using the following formula:
Where λ is the eigenvalue (the value on the diagonal) of the jordan-canonical matrix.
Spectral Decomposition
If we know all the eigenvalues of A, we can create our transition matrix T, and our inverse transition matrix T-1 These matrices will be the matrices of the right and left eigenvectors, respectively. If we have both the left and the right eigenvectors, we can calculate the state-transition matrix as:
[Spectral Decomposition]
Note that wi' is the transpose of the ith left-eigenvector, not the derivative of it. We will discuss the concepts of "eigenvalues", "eigenvectors", and the technique of spectral decomposition in more detail in a later chapter.
Cayley-Hamilton Theorem
Engineering Analysis
The Cayley-Hamilton Theorem can also be used to find a solution for a matrix exponential. For any eigenvalue of the system matrix A, λ, we can show that the two equations are equivalent:
Once we solve for the coefficients of the equation, a, we can then plug those coefficients into the following equation:
Example: Off-Diagonal Matrix
Given the following matrix A, find the state-transition matrix:
We can find the eigenvalues of this matrix as λ = i, -i. If we plug these values into our eigenvector equation, we get:
And we can solve for our eigenvectors:
With our eigenvectors, we can solve for our left-eigenvectors:
Now, using spectral decomposition, we can construct the state-transition matrix:
If we remember Euler's Identity, we can decompose the complex exponentials into sinusoids. Performing the vector multiplications, all the imaginary terms cancel out, and we are left with our result:
The reader is encouraged to perform the multiplications, and attempt to derive this result.
Example: Sympy Calculation
With the freely available python library 'sympy' we can very easily calculate the state-transition matrix automatically:
>>> from sympy import *
>>> t = symbols('t', positive = true)
>>> A = Matrix([[0,1],[-1,0]])
>>> exp(A*t).expand(complex=True)
⎡cos(t) sin(t)⎤
⎢ ⎥
⎣-sin(t) cos(t)⎦
You can also try it out yourself on this website:
Example: MATLAB Calculation
Using the symbolic toolbox in MATLAB, we can write MATLAB code to automatically generate the state-transition matrix for a given input matrix A. Here is an example of MATLAB code that can perform this task:
function [phi] = statetrans(A)
t = sym('t');
phi = expm(A * t);
end
Use this MATLAB function to find the state-transition matrix for the following matrices (warning, calculation may take some time):
Matrix 1 is a diagonal matrix, Matrix 2 has complex eigenvalues, and Matrix 3 is Jordan canonical form. These three matrices should be representative of some of the common forms of system matrices. The following code snippets are the input commands into MATLAB to produce these matrices, and the output results:
- Matrix A1
>> A1 = [2 0 ; 0 2]; >> statetrans(A1) ans = [ exp(2*t), 0] [ 0, exp(2*t)]
- Matrix A2
>> A2 = [0 1 ; -1 0]; >> statetrans(A1) ans = [ cos(t), sin(t)] [ -sin(t), cos(t)]
- Matrix A3
>> A1 = [2 1 ; 0 2]; >> statetrans(A1) ans = [ exp(2*t), t*exp(2*t)] [ 0, exp(2*t)]
Example: Multiple Methods in MATLAB
There are multiple methods in MATLAB to compute the state transtion matrix, from a scalar (time-invariant) matrix A. The following methods are all going to rely on the Symbolic Toolbox to perform the equation manipulations. At the end of each code snippet, the variable eAt contains the state-transition matrix of matrix A.
- Direct Method
t = sym('t');
eAt = expm(A * t);
- Laplace Transform Method
s = sym('s');
[n,n] = size(A);
in = inv(s*eye(n) - A);
eAt = ilaplace(in);
- Spectral Decomposition
t = sym('t');
[n,n] = size(A);
[V, e] = eig(A);
W = inv(V);
sum = [0 0;0 0];
for I = 1:n
sum = sum + expm(e(I,I)*t)*V(:,I)*W(I,:);
end;
eAt = sum;
All three of these methods should produce the same answers. The student is encouraged to verify this.
Time-Variant System Solutions
General Time Variant Solution
The state-space equations can be solved for time-variant systems, but the solution is significantly more complicated than the time-invariant case. Our time-variant state equation is given as follows:
We can say that the general solution to time-variant state-equation is defined as:
[Time-Variant General Solution]
Matrix Dimensions:
A: p × p
B: p × q
C: r × p
D: r × q
The function is called the state-transition matrix, because it (like the matrix exponential from the time-invariant case) controls the change for states in the state equation. However, unlike the time-invariant case, we cannot define this as a simple exponential. In fact, can't be defined in general, because it will actually be a different function for every system. However, the state-transition matrix does follow some basic properties that we can use to determine the state-transition matrix.
In a time-variant system, the general solution is obtained when the state-transition matrix is determined. For that reason, the first thing (and the most important thing) that we need to do here is find that matrix. We will discuss the solution to that matrix below.
State Transition Matrix
The state transition matrix is a matrix function of two variables (we will say t and τ). Once the form of the matrix is solved, we will plug in the initial time, t0 in place of the variable τ. Because of the nature of this matrix, and the properties that it must satisfy, this matrix typically is composed of exponential or sinusoidal functions. The exact form of the state-transition matrix is dependent on the system itself, and the form of the system's differential equation. There is no single "template solution" for this matrix.
The state transition matrix is not completely unknown, it must always satisfy the following relationships:
And also must have the following properties:
1. 2. 3. 4.
If the system is time-invariant, we can define as:
The reader can verify that this solution for a time-invariant system satisfies all the properties listed above. However, in the time-variant case, there are many different functions that may satisfy these requirements, and the solution is dependent on the structure of the system. The state-transition matrix must be determined before analysis on the time-varying solution can continue. We will discuss some of the methods for determining this matrix below.
Time-Variant, Zero Input
As the most basic case, we will consider the case of a system with zero input. If the system has no input, then the state equation is given as:
And we are interested in the response of this system in the time interval T = (a, b). The first thing we want to do in this case is find a fundamental matrix of the above equation. The fundamental matrix is related
Fundamental Matrix
Given the equation:
The solutions to this equation form an n-dimensional vector space in the interval T = (a, b). Any set of n linearly-independent solutions {x1, x2, ..., xn} to the equation above is called a fundamental set of solutions.
A fundamental matrix FM is formed by creating a matrix out of the n fundamental vectors. We will denote the fundamental matrix with a script capital X:
The fundamental matrix will satisfy the state equation:
Also, any matrix that solves this equation can be a fundamental matrix if and only if the determinant of the matrix is non-zero for all time t in the interval T. The determinant must be non-zero, because we are going to use the inverse of the fundamental matrix to solve for the state-transition matrix.
State Transition Matrix
Once we have the fundamental matrix of a system, we can use it to find the state transition matrix of the system:
The inverse of the fundamental matrix exists, because we specify in the definition above that it must have a non-zero determinant, and therefore must be non-singular. The reader should note that this is only one possible method for determining the state transition matrix, and we will discuss other methods below.
Example: 2-Dimensional System
Given the following fundamental matrix, Find the state-transition matrix.
the first task is to find the inverse of the fundamental matrix. Because the fundamental matrix is a 2 × 2 matrix, the inverse can be given easily through a common formula:
The state-transition matrix is given by:
Other Methods
There are other methods for finding the state transition matrix besides having to find the fundamental matrix.
- Method 1
- If A(t) is triangular (upper or lower triangular), the state transition matrix can be determined by sequentially integrating the individual rows of the state equation.
- Method 2
- If for every τ and t, the state matrix commutes as follows:
- Then the state-transition matrix can be given as:
- The state transition matrix will commute as described above if any of the following conditions are true:
- A is a constant matrix (time-invariant)
- A is a diagonal matrix
- If , where is a constant matrix, and f(t) is a scalar-valued function (not a matrix).
- If none of the above conditions are true, then you must use method 3.
- Method 3
- If A(t) can be decomposed as the following sum:
- Where Mi is a constant matrix such that MiMj = MjMi, and fi is a scalar-valued function. If A(t) can be decomposed in this way, then the state-transition matrix can be given as:
It will be left as an exercise for the reader to prove that if A(t) is time-invariant, that the equation in method 2 above will reduce to the state-transition matrix .
Example: Using Method 3
Use method 3, above, to compute the state-transition matrix for the system if the system matrix A is given by:
We can decompose this matrix as follows:
Where f1(t) = t, and f2(t) = 1. Using the formula described above gives us:
Solving the two integrations gives us:
The first term is a diagonal matrix, and the solution to that matrix function is all the individual elements of the matrix raised as an exponent of e. The second term can be decomposed as:
The final solution is given as:
Time-Variant, Non-zero Input
If the input to the system is not zero, it turns out that all the analysis that we performed above still holds. We can still construct the fundamental matrix, and we can still represent the system solution in terms of the state transition matrix .
We can show that the general solution to the state-space equations is actually the solution:
Eigenvalues and Eigenvectors
Eigenvalues and Eigenvectors
The eigenvalues and eigenvectors of the system matrix play a key role in determining the response of the system. It is important to note that only square matrices have eigenvalues and eigenvectors associated with them. Non-square matrices cannot be analyzed using the methods below.
The word "eigen" comes from German and means "own" as in "characteristic", so this chapter could also be called "Characteristic values and characteristic vectors". The terms "Eigenvalues" and "Eigenvectors" are most commonly used. Eigenvalues and Eigenvectors have a number of properties that make them valuable tools in analysis, and they also have a number of valuable relationships with the matrix from which they are derived. Computing the eigenvalues and the eigenvectors of the system matrix is one of the most important things that should be done when beginning to analyze a system matrix, second only to calculating the matrix exponential of the system matrix.
The eigenvalues and eigenvectors of the system determine the relationship between the individual system state variables (the members of the x vector), the response of the system to inputs, and the stability of the system. Also, the eigenvalues and eigenvectors can be used to calculate the matrix exponential of the system matrix through spectral decomposition. The remainder of this chapter will discuss eigenvalues, eigenvectors, and the ways that they affect their respective systems.
Characteristic Equation
The characteristic equation of the system matrix A is given as:
[Matrix Characteristic Equation]
Where λ are scalar values called the eigenvalues, and v are the corresponding eigenvectors. To solve for the eigenvalues of a matrix, we can take the following determinant:
To solve for the eigenvectors, we can then add an additional term, and solve for v:
Another value worth finding are the left eigenvectors of a system, defined as w in the modified characteristic equation:
[Left-Eigenvector Equation]
For more information about eigenvalues, eigenvectors, and left eigenvectors, read the appropriate sections in the following books:
Diagonalization
The transition matrix T should not be confused with the sampling time of a discrete system. If needed, we will use subscripts to differentiate between the two.
If the matrix A has a complete set of distinct eigenvalues, the matrix can be diagonalized. A diagonal matrix is a matrix that only has entries on the diagonal, and all the rest of the entries in the matrix are zero. We can define a transformation matrix, T, that satisfies the diagonalization transformation:
Which in turn will satisfy the relationship:
The right-hand side of the equation may look more complicated, but because D is a diagonal matrix here (not to be confused with the feed-forward matrix from the output equation), the calculations are much easier.
We can define the transition matrix, and the inverse transition matrix in terms of the eigenvectors and the left eigenvectors:
We will further discuss the concept of diagonalization later in this chapter.
Exponential Matrix Decomposition
Spectral Decomposition
A matrix exponential can be decomposed into a sum of the eigenvectors, eigenvalues, and left eigenvectors, as follows:
Notice that this equation only holds in this form if the matrix A has a complete set of n distinct eigenvalues. Since w'i is a row vector, and x(0) is a column vector of the initial system states, we can combine those two into a scalar coefficient α:
Since the state transition matrix determines how the system responds to an input, we can see that the system eigenvalues and eigenvectors are a key part of the system response. Let us plug this decomposition into the general solution to the state equation:
[State Equation Spectral Decomposition]
We will talk about this equation in the following sections.
State Relationship
As we can see from the above equation, the individual elements of the state vector x(t) cannot take arbitrary values, but they are instead related by weighted sums of multiples of the systems right-eigenvectors.
Decoupling
If a system can be designed such that the following relationship holds true:
then the system response from that particular eigenvalue will not be affected by the system input u, and we say that the system has been decoupled. Such a thing is difficult to do in practice.
Condition Number
With every matrix there is associated a particular number called the condition number of that matrix. The condition number tells a number of things about a matrix, and it is worth calculating. The condition number, k, is defined as:
[Condition Number]
Systems with smaller condition numbers are better, for a number of reasons:
- Large condition numbers lead to a large transient response of the system
- Large condition numbers make the system eigenvalues more sensitive to changes in the system.
We will discuss the issue of eigenvalue sensitivity more in a later section.
Stability
We will talk about stability at length in later chapters, but is a good time to point out a simple fact concerning the eigenvalues of the system. Notice that if the eigenvalues of the system matrix A are positive, or (if they are complex) that they have positive real parts, that the system state (and therefore the system output, scaled by the C matrix) will approach infinity as time t approaches infinity. In essence, if the eigenvalues are positive, the system will not satisfy the condition of BIBO stability, and will therefore become unstable.
Another factor that is worth mentioning is that a manufactured system never exactly matches the system model, and there will always been inaccuracies in the specifications of the component parts used, within a certain tolerance. As such, the system matrix will be slightly different from the mathematical model of the system (although good systems will not be severely different), and therefore the eigenvalues and eigenvectors of the system will not be the same values as those derived from the model. These facts give rise to several results:
- Systems with high condition numbers may have eigenvalues that differ by a large amount from those derived from the mathematical model. This means that the system response of the physical system may be very different from the intended response of the model.
- Systems with high condition numbers may become unstable simply as a result of inaccuracies in the component parts used in the manufacturing process.
For those reasons, the system eigenvalues and the condition number of the system matrix are highly important variables to consider when analyzing and designing a system. We will discuss the topic of stability in more detail in later chapters.
Non-Unique Eigenvalues
The decomposition above only works if the matrix A has a full set of n distinct eigenvalues (and corresponding eigenvectors). If A does not have n distinct eigenvectors, then a set of generalized eigenvectors need to be determined. The generalized eigenvectors will produce a similar matrix that is in Jordan canonical form, not the diagonal form we were using earlier.
Generalized Eigenvectors
Generalized eigenvectors can be generated using the following equation:
[Generalized Eigenvector Generating Equation]
if d is the number of times that a given eigenvalue is repeated, and p is the number of unique eigenvectors derived from those eigenvalues, then there will be q = d - p generalized eigenvectors. Generalized eigenvectors are developed by plugging in the regular eigenvectors into the equation above (vn). Some regular eigenvectors might not produce any non-trivial generalized eigenvectors. Generalized eigenvectors may also be plugged into the equation above to produce additional generalized eigenvectors. It is important to note that the generalized eigenvectors form an ordered series, and they must be kept in order during analysis or the results will not be correct.
Example: One Repeated Set
We have a 5 × 5 matrix A with eigenvalues . For , there is 1 distinct eigenvector a. For there is 1 distinct eigenvector b. From a, we generate the generalized eigenvector c, and from c we can generate vector d. From the eigevector b, we generate the generalized eigevector e. In order our eigenvectors are listed as:
- [a c d b e]
Notice how c and d are listed in order after the eigenvector that they are generated from, a. Also, we could reorder this as:
- [b e a c d]
because the generalized eigenvectors are listed in order after the regular eigenvector that they are generated from. Regular eigenvectors can be listed in any order.
Example: Two Repeated Sets
We have a 4 × 4 matrix A with eigenvalues . For we have two eigevectors, a and b. For we have an eigenvector c.
We need to generate a fourth eigenvector, d. The only eigenvalue that needs another eigenvector is , however there are already two eigevectors associated with that eigenvalue, and only one of them will generate a non-trivial generalized eigenvector. To figure out which one works, we need to plug both vectors into the generating equation:
If a generates the correct vector d, we will order our eigenvectors as:
- [a d b c]
but if b generates the correct vector, we can order it as:
- [a b d c]
Jordan Canonical Form
Matrix Forms
If a matrix has a complete set of distinct eigenvectors, the transition matrix T can be defined as the matrix of those eigenvectors, and the resultant transformed matrix will be a diagonal matrix. However, if the eigenvectors are not unique, and there are a number of generalized eigenvectors associated with the matrix, the transition matrix T will consist of the ordered set of the regular eigenvectors and generalized eigenvectors. The regular eigenvectors that did not produce any generalized eigenvectors (if any) should be first in the order, followed by the eigenvectors that did produce generalized eigenvectors, and the generalized eigenvectors that they produced (in appropriate sequence).
Once the T matrix has been produced, the matrix can be transformed by it and it's inverse:
The J matrix will be a Jordan block matrix. The format of the Jordan block matrix will be as follows:
Where D is the diagonal block produced by the regular eigenvectors that are not associated with generalized eigenvectors (if any). The Jn blocks are standard Jordan blocks with a size corresponding to the number of eigenvectors/generalized eigenvectors in each sequence. In each Jn block, the eigenvalue associated with the regular eigenvector of the sequence is on the main diagonal, and there are 1's in the sub-diagonal.
System Response
Equivalence Transformations
If we have a non-singular n × n matrix P, we can define a transformed vector "x bar" as:
We can transform the entire state-space equation set as follows:
Where:
We call the matrix P the equivalence transformation between the two sets of equations.
It is important to note that the eigenvalues of the matrix A (which are of primary importance to the system) do not change under the equivalence transformation. The eigenvectors of A, and the eigenvectors of are related by the matrix P.
Lyapunov Transformations
The transformation matrix P is called a Lyapunov Transformation if the following conditions hold:
- P(t) is nonsingular.
- P(t) and P'(t) are continuous
- P(t) and the inverse transformation matrix P-1(t) are finite for all t.
If a system is time-variant, it can frequently be useful to use a Lyapunov transformation to convert the system to an equivalent system with a constant A matrix. This is not always possible in general, however it is possible if the A(t) matrix is periodic.
System Diagonalization
If the A matrix is time-invariant, we can construct the matrix V from the eigenvectors of A. The V matrix can be used to transform the A matrix to a diagonal matrix. Our new system becomes:
Since our system matrix is now diagonal (or Jordan canonical), the calculation of the state-transition matrix is simplified:
Where Λ is a diagonal matrix.
MATLAB Transformations
The MATLAB function ss2ss can be used to apply an equivalence transformation to a system. If we have a set of matrices A, B, C and D, we can create equivalent matrices as such:
[Ap, Bp, Cp, Dp] = ss2ss(A, B, C, D, p);
Where p is the equivalence transformation matrix.
MIMO Systems
Multi-Input, Multi-Output
Systems with more than one input and/or more than one output are known as Multi-Input Multi-Output systems, or they are frequently known by the abbreviation MIMO. This is in contrast to systems that have only a single input and a single output (SISO), like we have been discussing previously.
State-Space Representation
MIMO systems that are lumped and linear can be described easily with state-space equations. To represent multiple inputs we expand the input u(t) into a vector U(t) with the desired number of inputs. Likewise, to represent a system with multiple outputs, we expand y(t) into Y(t), which is a vector of all the outputs. For this method to work, the outputs must be linearly dependent on the input vector and the state vector.
Example: Two Inputs and Two Outputs
Let's say that we have two outputs, y1 and y2, and two inputs, u1 and u2. These are related in our system through the following system of differential equations:
now, we can assign our state variables as such, and produce our first-order differential equations:
And finally we can assemble our state space equations:
Transfer Function Matrix
If the system is LTI and Lumped, we can take the Laplace Transform of the state-space equations, as follows:
Which gives us the result:
Where X(0) is the initial conditions of the system state vector in the time domain. If the system is relaxed, we can ignore this term, but for completeness we will continue the derivation with it.
We can separate out the variables in the state equation as follows:
Then factor out an X(s):
And then we can multiply both sides by the inverse of [sI - A] to give us our state equation:
Now, if we plug in this value for X(s) into our output equation, above, we get a more complicated equation:
And we can distribute the matrix C to give us our answer:
Now, if the system is relaxed, and therefore X(0) is 0, the first term of this equation becomes 0. In this case, we can factor out a U(s) from the remaining two terms:
We can make the following substitution to obtain the Transfer Function Matrix, or more simply, the Transfer Matrix, H(s):
[Transfer Matrix]
And rewrite our output equation in terms of the transfer matrix as follows:
[Transfer Matrix Description]
If Y(s) and X(s) are 1 × 1 vectors (a SISO system), then we have our external description:
Now, since X(s) = X(s), and Y(s) = Y(s), then H(s) must be equal to H(s). These are simply two different ways to describe the same exact equation, the same exact system.
Dimensions
If our system has q inputs, and r outputs, our transfer function matrix will be an r × q matrix.
Relation to Transfer Function
For SISO systems, the Transfer Function matrix will reduce to the transfer function as would be obtained by taking the Laplace transform of the system response equation.
For MIMO systems, with n inputs and m outputs, the transfer function matrix will contain n × m transfer functions, where each entry is the transfer function relationship between each individual input, and each individual output.
Through this derivation of the transfer function matrix, we have shown the equivalency between the Laplace methods and the State-Space method for representing systems. Also, we have shown how the Laplace method can be generalized to account for MIMO systems. Through the rest of this explanation, we will use the Laplace and State Space methods interchangeably, opting to use one or the other where appropriate.
Zero-State and Zero-Input
If we have our complete system response equation from above:
We can separate this into two separate parts:
- The Zero-Input Response.
- The Zero-State Response.
These are named because if there is no input to the system (zero-input), then the output is the response of the system to the initial system state. If there is no state to the system, then the output is the response of the system to the system input. The complete response is the sum of the system with no input, and the input with no state.
Discrete MIMO Systems
In the discrete case, we end up with similar equations, except that the X(0) initial conditions term is preceded by an additional z variable:
If X(0) is zero, that term drops out, and we can derive a Transfer Function Matrix in the Z domain as well:
[Transfer Matrix]
[Transfer Matrix Description]
Example: Pulse Response
For digital systems, it is frequently a good idea to write the pulse response equation, from the state-space equations:
We can combine these two equations into a single difference equation using the coefficient matrices A, B, C, and D. To do this, we find the ratio of the system output vector, Y[n], to the system input vector, U[n]:
So the system response to a digital system can be derived from the pulse response equation by:
And we can set U(z) to a step input through the following Z transform:
Plugging this into our pulse response we get our step response:
Controller Design
The controller design for MIMO systems is more extensive and thus more complicated than for SISO system. Ackermann's formula, the typical full state feedback design for SISO system, could not be used for MIMO systems because the additional inputs lead to an overdetermined system. This means, in case of MIMO systems, the feedback matrix K is not unique.
Approaches for the controller design are stated in Section Eigenvalue Assignment for MIMO Systems.
System Realization
Realization
Realization is the process of taking a mathematical model of a system (either in the Laplace domain or the State-Space domain), and creating a physical system. Some systems are not realizable.
An important point to keep in mind is that the Laplace domain representation, and the state-space representations are equivalent, and both representations describe the same physical systems. We want, therefore, a way to convert between the two representations, because each one is well suited for particular methods of analysis.
The state-space representation, for instance, is preferable when it comes time to move the system design from the drawing board to a constructed physical device. For that reason, we call the process of converting a system from the Laplace representation to the state-space representation "realization".
Realization Conditions
Discrete systems G(z) are also realizable if these conditions are satisfied.
- A transfer function G(s) is realizable if and only if the system can be described by a finite-dimensional state-space equation.
- (A B C D), an ordered set of the four system matrices, is called a realization of the system G(s). If the system can be expressed as such an ordered quadruple, the system is realizable.
- A system G is realizable if and only if the transfer matrix G(s) is a proper rational matrix. In other words, every entry in the matrix G(s) (only 1 for SISO systems) is a rational polynomial, and if the degree of the denominator is higher or equal to the degree of the numerator.
We've already covered the method for realizing a SISO system, the remainder of this chapter will talk about the general method of realizing a MIMO system.
Realizing the Transfer Matrix
We can decompose a transfer matrix G(s) into a strictly proper transfer matrix:
Where Gsp(s) is a strictly proper transfer matrix. Also, we can use this to find the value of our D matrix:
We can define d(s) to be the lowest common denominator polynomial of all the entries in G(s):
Then we can define Gsp as:
Where
And the Ni are p × q constant matrices.
If we remember our method for converting a transfer function to a state-space equation, we can follow the same general method, except that the new matrix A will be a block matrix, where each block is the size of the transfer matrix:
Realizing System by Column
We can divide the G(s) into multiple column, realize them individually and join them back together later, for G(s):
where we realize them and yield:
and the realization of the system will be:
System Representation
Systems can be represented graphically in a number of ways. Block diagrams and signal-flow diagrams are powerful tools that can be used to manipulate systems, and convert them easily into transfer functions or state-space equations. The chapters in this section will discuss how systems can be described visually, and will also discuss how systems can be interconnected with each other.
Gain
What is Gain?
Gain is a proportional value that shows the relationship between the magnitude of the input to the magnitude of the output signal at steady state. Many systems contain a method by which the gain can be altered, providing more or less "power" to the system. However, increasing gain or decreasing gain beyond a particular safety zone can cause the system to become unstable.
Consider the given second-order system:
We can include an arbitrary gain term, K in this system that will represent an amplification, or a power increase:
In a state-space system, the gain term k can be inserted as follows:
The gain term can also be inserted into other places in the system, and in those cases the equations will be slightly different.

Example: Gain
Here are some good examples of arbitrary gain values being used in physical systems:
- Volume Knob
- On your stereo there is a volume knob that controls the gain of your amplifier circuit. Higher levels of volume (turning the volume "up") corresponds to higher amplification of the sound signal.
- Gas Pedal
- The gas pedal in your car is an example of gain. Pressing harder on the gas pedal causes the engine to receive more gas, and causes the engine to output higher RPMs.
- Brightness Buttons
- Most computer monitors come with brightness buttons that control how bright the screen image is. More brightness causes more power to be outputed to the screen.
Responses to Gain
As the gain to a system increases, generally the rise-time decreases, the percent overshoot increases, and the settling time increases. However, these relationships are not always the same. A critically damped system, for example, may decrease in rise time while not experiencing any effects of percent overshoot or settling time.
Gain and Stability
If the gain increases to a high enough extent, some systems can become unstable. We will examine this effect in the chapter on Root Locus. But it will decrease the steady state error.
Conditional Stability
Systems that are stable for some gain values, and unstable for other values are called conditionally stable systems. The stability is conditional upon the value of the gain, and often the threshold where the system becomes unstable is important to find.
Block Diagrams
When designing or analyzing a system, often it is useful to model the system graphically. Block Diagrams are a useful and simple method for analyzing a system graphically. A "block" looks on paper exactly what it means:
Systems in Series
When two or more systems are in series, they can be combined into a single representative system, with a transfer function that is the product of the individual systems.

If we have two systems, f(t) and g(t), we can put them in series with one another so that the output of system f(t) is the input to system g(t). Now, we can analyze them depending on whether we are using our classical or modern methods.
If we define the output of the first system as h(t), we can define h(t) as:
Now, we can define the system output y(t) in terms of h(t) as:
We can expand h(t):
But, since convolution is associative, we can re-write this as:
Our system can be simplified therefore as such:

Series Transfer Functions
If two or more systems are in series with one another, the total transfer function of the series is the product of all the individual system transfer functions.

In the time-domain we know that:
But, in the frequency domain we know that convolution becomes multiplication, so we can re-write this as:
We can represent our system in the frequency domain as:
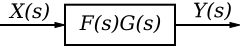
Series State Space
If we have two systems in series (say system F and system G), where the output of F is the input to system G, we can write out the state-space equations for each individual system.
System 1:
System 2:
And we can write substitute these equations together form the complete response of system H, that has input u, and output yG:
[Series state equation]
[Series output equation]
Systems in Parallel

Blocks may not be placed in parallel without the use of an adder. Blocks connected by an adder as shown above have a total transfer function of:
Since the Laplace transform is linear, we can easily transfer this to the time domain by converting the multiplication to convolution:

State Space Model
The state-space equations, with non-zero A, B, C, and D matrices conceptually model the following system:

In this image, the strange-looking block in the center is either an integrator or an ideal delay, and can be represented in the transfer domain as:
- or
Depending on the time characteristics of the system. If we only consider continuous-time systems, we can replace the funny block in the center with an integrator:
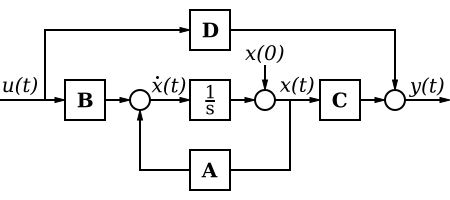
In the Laplace Domain
The state space model of the above system, if A, B, C, and D are transfer functions A(s), B(s), C(s) and D(s) of the individual subsystems, and if U(s) and Y(s) represent a single input and output, can be written as follows:
We will explain how we got this result, and how we deal with feedforward and feedback loop structures in the next chapter.
Adders and Multipliers
Some systems may have dedicated summation or multiplication devices, that automatically add or multiply the transfer functions of multiple systems together
Simplifying Block Diagrams
Block diagrams can be systematically simplified. Note that this table is from Schaum's Outline: Feedback and Controls Systems by DiStefano et al
External links
Feedback Loops
Feedback
A feedback loop is a common and powerful tool when designing a control system. Feedback loops take the system output into consideration, which enables the system to adjust its performance to meet a desired output response.
When talking about control systems it is important to keep in mind that engineers typically are given existing systems such as actuators, sensors, motors, and other devices with set parameters, and are asked to adjust the performance of those systems. In many cases, it may not be possible to open the system (the "plant") and adjust it from the inside: modifications need to be made external to the system to force the system response to act as desired. This is performed by adding controllers, compensators, and feedback structures to the system.
Basic Feedback Structure
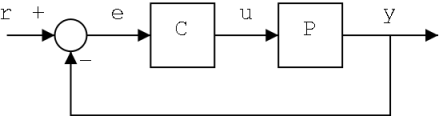
This is a basic feedback structure. Here, we are using the output value of the system to help us prepare the next output value. In this way, we can create systems that correct errors. Here we see a feedback loop with a value of one. We call this a unity feedback.
Here is a list of some relevant vocabulary, that will be used in the following sections:
- Plant
- The term "Plant" is a carry-over term from chemical engineering to refer to the main system process. The plant is the preexisting system that does not (without the aid of a controller or a compensator) meet the given specifications. Plants are usually given "as is", and are not changeable. In the picture above, the plant is denoted with a P.
- Controller
- A controller, or a "compensator" is an additional system that is added to the plant to control the operation of the plant. The system can have multiple compensators, and they can appear anywhere in the system: Before the pick-off node, after the summer, before or after the plant, and in the feedback loop. In the picture above, our compensator is denoted with a C.
- Summer
- A summer is a symbol on a system diagram, (denoted above with parenthesis) that conceptually adds two or more input signals, and produces a single sum output signal.
- Pick-off node
- A pickoff node is simply a fancy term for a split in a wire.
- Forward Path
- The forward path in the feedback loop is the path after the summer, that travels through the plant and towards the system output.
- Reverse Path
- The reverse path is the path after the pick-off node, that loops back to the beginning of the system. This is also known as the "feedback path".
- Unity feedback
- When the multiplicative value of the feedback path is 1.
Negative vs Positive Feedback
It turns out that negative feedback is almost always the most useful type of feedback. When we subtract the value of the output from the value of the input (our desired value), we get a value called the error signal. The error signal shows us how far off our output is from our desired input.
Positive feedback has the property that signals tend to reinforce themselves, and grow larger. In a positive feedback system, noise from the system is added back to the input, and that in turn produces more noise. As an example of a positive feedback system, consider an audio amplification system with a speaker and a microphone. Placing the microphone near the speaker creates a positive feedback loop, and the result is a sound that grows louder and louder. Because the majority of noise in an electrical system is high-frequency, the sound output of the system becomes high-pitched.
Example: State-Space Equation
In the previous chapter, we showed you this picture:
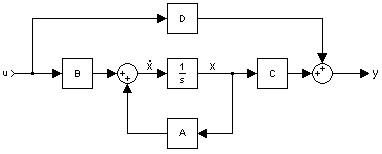
Now, we will derive the I/O relationship into the state-space equations. If we examine the inner-most feedback loop, we can see that the forward path has an integrator system, , and the feedback loop has the matrix value A. If we take the transfer function only of this loop, we get:
Pre-multiplying by the factor B, and post-multiplying by C, we get the transfer function of the entire lower-half of the loop:
We can see that the upper path (D) and the lower-path Tlower are added together to produce the final result:
Now, for an alternate method, we can assume that x' is the value of the inner-feedback loop, right before the integrator. This makes sense, since the integral of x' should be x (which we see from the diagram that it is. Solving for x', with an input of u, we get:
This is because the value coming from the feedback branch is equal to the value x times the feedback loop matrix A, and the value coming from the left of the summer is the input u times the matrix B.
If we keep things in terms of x and u, we can see that the system output is the sum of u times the feed-forward value D, and the value of x times the value C:
These last two equations are precisely the state-space equations of our system.
Feedback Loop Transfer Function
We can solve for the output of the system by using a series of equations:
and when we solve for Y(s) we get:
[Feedback Transfer Function]
The reader is encouraged to use the above equations to derive the result by themselves.
The function E(s) is known as the error signal. The error signal is the difference between the system output (Y(s)), and the system input (X(s)). Notice that the error signal is now the direct input to the system G(s). X(s) is now called the reference input. The purpose of the negative feedback loop is to make the system output equal to the system input, by identifying large differences between X(s) and Y(s) and correcting for them.
Example: Elevator
Here is a simple example of reference inputs and feedback systems:
There is an elevator in a certain building with 5 floors. Pressing button "1" will take you to the first floor, and pressing button "5" will take you to the fifth floor, etc. For reasons of simplicity, only one button can be pressed at a time.
Pressing a particular button is the reference input of the system. Pressing "1" gives the system a reference input of 1, pressing "2" gives the system a reference input of 2, etc. The elevator system then, tries to make the output (the physical floor location of the elevator) match the reference input (the button pressed in the elevator). The error signal, e(t), represents the difference between the reference input x(t), and the physical location of the elevator at time t, y(t).
Let's say that the elevator is on the first floor, and the button "5" is pressed at time t0. The reference input then becomes a step function:
Where we are measuring in units of "floors". At time t0, the error signal is:
Which means that the elevator needs to travel upwards 4 more floors. At time t1, when the elevator is at the second floor, the error signal is:
Which means the elevator has 3 more floors to go. Finally, at time t4, when the elevator reaches the top, the error signal is:
And when the error signal is zero, the elevator stops moving. In essence, we can define three cases:
- e(t) is positive: In this case, the elevator goes up one floor, and checks again.
- e(t) is zero: The elevator stops.
- e(t) is negative: The elevator goes down one floor, and checks again.
State-Space Feedback Loops
In the state-space representation, the plant is typically defined by the state-space equations:
The plant is considered to be pre-existing, and the matrices A, B, C, and D are considered to be internal to the plant (and therefore unchangeable). Also, in a typical system, the state variables are either fictional (in the sense of dummy-variables), or are not measurable. For these reasons, we need to add external components, such as a gain element, or a feedback element to the plant to enhance performance.
Consider the addition of a gain matrix K installed at the input of the plant, and a negative feedback element F that is multiplied by the system output y, and is added to the input signal of the plant. There are two cases:
- The feedback element F is subtracted from the input before multiplication of the K gain matrix.
- The feedback element F is subtracted from the input after multiplication of the K gain matrix.
In case 1, the feedback element F is added to the input before the multiplicative gain is applied to the input. If v is the input to the entire system, then we can define u as:
In case 2, the feeback element F is subtracted from the input after the multiplicative gain is applied to the input. If v is the input to the entire system, then we can define u as:
Open Loop vs Closed Loop
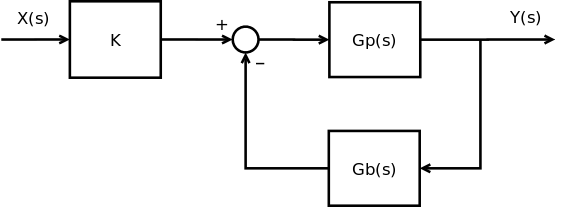
Let's say that we have the generalized system shown above. The top part, Gp(s) represents all the systems and all the controllers on the forward path. The bottom part, Gb(s) represents all the feedback processing elements of the system. The letter "K" in the beginning of the system is called the Gain. We will talk about the gain more in later chapters. We can define the Closed-Loop Transfer Function as follows:
[Closed-Loop Transfer Function]
If we "open" the loop, and break the feedback node, we can define the Open-Loop Transfer Function, as:
[Open-Loop Transfer Function]
We can redefine the closed-loop transfer function in terms of this open-loop transfer function:
These results are important, and they will be used without further explanation or derivation throughout the rest of the book.
Placement of a Controller
There are a number of different places where we could place an additional controller.
Each location has certain benefits and problems, and hopefully we will get a chance to talk about all of them.
Second-Order Systems
The general expression of the transfer function of a second order system is given as:
where and are damping ratio and natural frequency of the system respectively.
Damping Ratio
The damping ratio is defined by way of the sign . The damping ratio gives us an idea about the nature of the transient response detailing the amount of overshoot & oscillation that the system will undergo. This is completely regardless of time scaling.
If :
- = zero, the system is undamped;
- < 1, the system is underdamped;
- = 1, the system is critically damped;
- > 1, the system is overdamped.
is used in conjunction with the natural frequency to determine system properties. To find the zeta value you must first find the natural response!
Natural Frequency
Natural Frequency, denoted by is defined as the frequency with which the system would oscillate if it were not damped and we define the damping ratio as .
System Sensitivity
Signal Flow Diagrams
Signal-flow graphs
Signal-flow graphs are another method for visually representing a system. Signal Flow Diagrams are especially useful, because they allow for particular methods of analysis, such as Mason's Gain Formula.
Signal flow diagrams typically use curved lines to represent wires and systems, instead of using lines at right-angles, and boxes, respectively. Every curved line is considered to have a multiplier value, which can be a constant gain value, or an entire transfer function. Signals travel from one end of a line to the other, and lines that are placed in series with one another have their total multiplier values multiplied together (just like in block diagrams).
Signal flow diagrams help us to identify structures called "loops" in a system, which can be analyzed individually to determine the complete response of the system.

Forward Paths
A forward path is a path in the signal flow diagram that connects the input to the output without touching any single node or path more than once. A single system can have multiple forward paths.
Loops
A loop is a structure in a signal flow diagram that leads back to itself. A loop does not contain the beginning and ending points, and the end of the loop is the same node as the beginning of a loop.
Loops are said to touch if they share a node or a line in common.
The Loop gain is the total gain of the loop, as you travel from one point, around the loop, back to the starting point.
Delta Values
The Delta value of a system, denoted with a Greek Δ is computed as follows:
Where:
- A is the sum of all individual loop gains
- B is the sum of the products of all the pairs of non-touching loops
- C is the sum of the products of all the sets of 3 non-touching loops
- D is the sum of the products of all the sets of 4 non-touching loops
- et cetera.
If the given system has no pairs of loops that do not touch, for instance, B and all additional letters after B will be zero.
Mason's Rule
Mason's rule is a rule for determining the gain of a system. Mason's rule can be used with block diagrams, but it is most commonly (and most easily) used with signal flow diagrams.
If we have computed our delta values (above), we can then use Mason's Gain Rule to find the complete gain of the system:
[Mason's Rule]
Where M is the total gain of the system, represented as the ratio of the output gain (yout) to the input gain (yin) of the system. Mk is the gain of the kth forward path, and Δk is the loop gain of the kth loop.
Examples
Solving a signal-flow graph by systematic reduction : Two interlocking loops
This example shows how a system of five equations in five unknowns is solved using systematic reduction rules. The independent variable is . The dependent variables are , , , , . The coefficients are labeled .
Here is the starting flowgraph:
The steps for solving follow.
Removing edge c from x2 to x3
Removing node x2 and its inflows
has no outflows, and is not a node of interest.


Removing edge e from x3 to x1
Remove edge d from x3 to x4
Node has no outflows and is not a node of interest. It is deleted along with its inflows.
Removing self-loop at x1
Removing self-loop at x4
Remove edge from x4 to x1
Remove outflow from x4 to xout
's outflow is then eliminated: is connected directly to using the product of the gains from the two edges replaced.
is not a variable of interest; thus, its node and its inflows are eliminated.
Eliminating self-loop at x1
Eliminating outflow from x1, then eliminating x1 and its inflows
is not a variable of interest; and its inflows are eliminated
Simplifying the gain expression
Solving a signal-flow graph by systematic reduction: Three equations in three unknowns
This example shows how a system of three equations in three unknowns is solved using systematic reduction rules.
The independent variables are , , . The dependent variables are , , . The coefficients are labeled . The steps for solving follow:
Electrical engineering: Construction of a flow graph for a RC circuit
This illustration shows the physical connections of the circuit. Independent voltage source S is connected in series with a resistor R and capacitor C. The example is developed from the physical circuit equations and solved using signal-flow graph techniques. Polarity is important:
- S is a source with the positive terminal at N1 and the negative terminal at N3
- R is a resistor with the positive terminal at N1 and the negative terminal at N2
- C is a capacitor with the positive terminal at N2 and the negative terminal at N3.
The unknown variable of interest is the voltage across capacitor C.
Approach to the solution:
- Find the set of equations from the physical network. These equations are acausal in nature.
- Branch equations for the capacitor and resistor. The equations will be developed as transfer functions using Laplace transforms.
- Kirchhoff's voltage and current laws
- Build a signal-flow graph from the equations.
- Solve the signal-flow graph.
Branch equations
 The branch equations are shown for R and C.
The branch equations are shown for R and C.
Resistor R (Branch equation )
The resistor's branch equation in the time domain is:
In the Laplace-transformed signal space:
Capacitor C (Branch equation )
The capacitor's branch equation in the time domain is:
Assuming the capacitor is initially discharged, the equation becomes:
Taking the derivative of this and multiplying by C yields the derivative form:
In the Laplace-transformed signal space:
Kirchhoff's laws equations
Kirchhoff's Voltage Law equation
This circuit has only one independent loop. Its equation in the time domain is:
In the Laplace-transformed signal space:
Kirchhoff's Current Law equations
The circuit has three nodes, thus three Kirchhoff's current equations (expresses here as the currents flowing from the nodes):
In the Laplace-transformed signal space:
A set of independent equations must be chosen. For the current laws, it is necessary to drop one of these equations. In this example, let us choose .
Building the signal-flow graph
We then look at the inventory of equations, and the signals that each equation relates:
| Equation | Signals |
|---|---|
The next step consists in assigning to each equation a signal that will be represented as a node. Each independent source signal is represented in the signal-flow graph as a source node, therefore no equation is assigned to the independent source . There are many possible valid signal flow graphs from this set of equations. An equation must only be used once, and the variables of interest must be represented.
| Equation | Signals | Assigned signal node |
|---|---|---|
The resulting flow graph is then drawn
The next step consists in solving the signal-flow graph.
Using either Mason or systematic reduction, the resulting signal flow graph is:

Mechatronics example

Bode Plots
Bode Plots
A Bode Plot is a useful tool that shows the gain and phase response of a given LTI system for different frequencies. Bode Plots are generally used with the Fourier Transform of a given system.

The frequency of the bode plots are plotted against a logarithmic frequency axis. Every tickmark on the frequency axis represents a power of 10 times the previous value. For instance, on a standard Bode plot, the values of the markers go from (0.1, 1, 10, 100, 1000, ...) Because each tickmark is a power of 10, they are referred to as a decade. Notice that the "length" of a decade decreases as you move to the right on the graph. (note that this description doesn't match the chart above... there are 10 tickmarks per decade, not one, but since it is a log chart they are not evenly spaced).
The bode Magnitude plot measures the system Input/Output ratio in special units called decibels. The Bode phase plot measures the phase shift in degrees (typically, but radians are also used).
Decibels
A Decibel is a ratio between two numbers on a logarithmic scale. To express a ratio between two numbers (A and B) as a decibel we apply the following formula for numbers that represent amplitudes (numbers that represent a power measurement use a factor of 10 rather than 20):
Where dB is the decibel result.
Or, if we just want to take the decibels of a single number C, we could just as easily write:
Frequency Response Notations
If we have a system transfer function T(s), we can separate it into a numerator polynomial N(s) and a denominator polynomial D(s). We can write this as follows:
To get the magnitude gain plot, we must first transit the transfer function into the frequency response by using the change of variables:
From here, we can say that our frequency response is a composite of two parts, a real part R and an imaginary part X:
We will use these forms below.
Straight-Line Approximations
The Bode magnitude and phase plots can be quickly and easily approximated by using a series of straight lines. These approximate graphs can be generated by following a few short, simple rules (listed below). Once the straight-line graph is determined, the actual Bode plot is a smooth curve that follows the straight lines, and travels through the breakpoints.
Break Points
If the frequency response is in pole-zero form:
We say that the values for all zn and pm are called break points of the Bode plot. These are the values where the Bode plots experience the largest change in direction.
Break points are sometimes also called "break frequencies", "cutoff points", or "corner points".
Bode Gain Plots
Bode Gain Plots, or Bode Magnitude Plots display the ratio of the system gain at each input frequency.
Bode Gain Calculations
The magnitude of the transfer function T is defined as:
However, it is frequently difficult to transition a function that is in "numerator/denominator" form to "real+imaginary" form. Luckily, our decibel calculation comes in handy. Let's say we have a frequency response defined as a fraction with numerator and denominator polynomials defined as:
If we convert both sides to decibels, the logarithms from the decibel calculations convert multiplication of the arguments into additions, and the divisions into subtractions:
And calculating out the gain of each term and adding them together will give the gain of the system at that frequency.
Bode Gain Approximations
The slope of a straight line on a Bode magnitude plot is measured in units of dB/Decade, because the units on the vertical axis are dB, and the units on the horizontal axis are decades.
The value ω = 0 is infinitely far to the left of the bode plot (because a logarithmic scale never reaches zero), so finding the value of the gain at ω = 0 essentially sets that value to be the gain for the Bode plot from all the way on the left of the graph up till the first break point. The value of the slope of the line at ω = 0 is 0 dB/Decade.
From each pole break point, the slope of the line decreases by 20 dB/Decade. The line is straight until it reaches the next break point. From each zero break point the slope of the line increases by 20 dB/Decade. Double, triple, or higher amounts of repeat poles and zeros affect the gain by multiplicative amounts. Here are some examples:
- 2 poles: -40 dB/Decade
- 10 poles: -200 dB/Decade
- 5 zeros: +100 dB/Decade
Bode Phase Plots
Bode phase plots are plots of the phase shift to an input waveform dependent on the frequency characteristics of the system input. Again, the Laplace transform does not account for the phase shift characteristics of the system, but the Fourier Transform can. The phase of a complex function, in "real+imaginary" form is given as:
Bode Procedure
Given a frequency response in pole-zero form:
Where A is a non-zero constant (can be negative or positive).
Here are the steps involved in sketching the approximate Bode magnitude plots:
Bode Magnitude Plots
- Step 1
- Factor the transfer function into pole-zero form.
- Step 2
- Find the frequency response from the Transfer function.
- Step 3
- Use logarithms to separate the frequency response into a sum of decibel terms
- Step 4
- Use to find the starting magnitude.
- Step 5
- The locations of every pole and every zero are called break points. At a zero breakpoint, the slope of the line increases by 20dB/Decade. At a pole, the slope of the line decreases by 20dB/Decade.
- Step 6
- At a zero breakpoint, the value of the actual graph differs from the value of the straight-line graph by 3dB. A zero is +3dB over the straight line, and a pole is -3dB below the straight line.
- Step 7
- Sketch the actual bode plot as a smooth-curve that follows the straight lines of the previous point, and travels through the breakpoints.
Here are the steps to drawing the Bode phase plots:
Bode Phase Plots
- Step 1
- If A is positive, start your graph (with zero slope) at 0 degrees. If A is negative, start your graph with zero slope at 180 degrees (or -180 degrees, they are the same thing).
- Step 2
- For every zero, slope the line up at 45 degrees per decade when (1 decade before the break frequency). Multiple zeros means the slope is steeper.
- Step 3
- For every pole, slope the line down at 45 degrees per decade when (1 decade before the break frequency). Multiple poles means the slope is steeper.
- Step 4
- Flatten the slope again when the phase has changed by 90 degrees (for a zero) or -90 degrees (for a pole) (or larger values, for multiple poles or multiple zeros.
Examples
Example: Constant Gain
Draw the bode plot of an amplifier system, with a constant gain increase of 6dB.
Because the gain value is constant, and is not dependent on the frequency, we know that the value of the magnitude graph is constant at all places on the graph. There are no break points, so the slope of the graph never changes. We can draw the graph as a straight, horizontal line at 6dB:
Example: Integrator
Draw the bode plot of a perfect integrator system given by the transfer function:
First, we find the frequency response of the system, by a change of variables:
Then we convert our magnitude into logarithms:
Notice that the location of the break point for the pole is located at ω → 0, which is all the way to the left of the graph. Also, we notice that inserting 0 in for ω gives us an undefined value (which approaches negative infinity, as the limit). We know, because there is a single pole at zero, that the graph to the right of zero (which is everywhere) has a slope of -20dB/Decade. We can determine from our magnitude calculation by plugging in ω → 1 that the second term drops out, and the magnitude at that point is 6dB. We now have the slope of the line, and a point that it intersects, and we can draw the graph:
Example: Differentiator
Example: 1st Order, Low-pass Filter (1 Break Point)
Further reading
Nichols Charts
Nichols Charts
This page will talk about the use of Nichols charts to analyze frequency-domain characteristics of control systems.
Stability
System stability is an important topic, because unstable systems may not perform correctly, and may actually be harmful to people. There are a number of different methods and tools that can be used to determine system stability, depending on whether you are in the state-space, or the complex domain.
Stability
Stability
When a system is unstable, the output of the system may be infinite even though the input to the system was finite. This causes a number of practical problems. For instance, a robot arm controller that is unstable may cause the robot to move dangerously. Also, systems that are unstable often incur a certain amount of physical damage, which can become costly. Nonetheless, many systems are inherently unstable - a fighter jet, for instance, or a rocket at liftoff, are examples of naturally unstable systems. Although we can design controllers that stabilize the system, it is first important to understand what stability is, how it is determined, and why it matters.
The chapters in this section are heavily mathematical and many require a background in linear differential equations. Readers without a strong mathematical background might want to review the necessary chapters in the Calculus and Ordinary Differential Equations books (or equivalent) before reading this material.
For most of this chapter we will be assuming that the system is linear and can be represented either by a set of transfer functions or in state space. Linear systems have an associated characteristic polynomial which tells us a great deal about the stability of the system. If any coefficient of the characteristic polynomial is zero or negative then the system is either unstable or at most marginally stable. It is important to note that even if all of the coefficients of the characteristic polynomial are positive the system may still be unstable. We will look into this in more detail below.
BIBO Stability
A system is defined to be BIBO Stable if every bounded input to the system results in a bounded output over the time interval . This must hold for all initial times to. So long as we don't input infinity to our system, we won't get infinity output.
A system is defined to be uniformly BIBO Stable if there exists a positive constant k that is independent of t0 such that for all t0 the following conditions:
implies that
There are a number of different types of stability, and keywords that are used with the topic of stability. Some of the important words that we are going to be discussing in this chapter, and the next few chapters are: BIBO Stable, Marginally Stable, Conditionally Stable, Uniformly Stable, Asymptotically Stable, and Unstable. All of these words mean slightly different things.
Determining BIBO Stability
We can prove mathematically that a system f is BIBO stable if an arbitrary input x is bounded by two finite but large arbitrary constants M and -M:
We apply the input x, and the arbitrary boundaries M and -M to the system to produce three outputs:
Now, all three outputs should be finite for all possible values of M and x, and they should satisfy the following relationship:
If this condition is satisfied, then the system is BIBO stable.
A SISO linear time-invariant (LTI) system is BIBO stable if and only if is absolutely integrable from [0,∞] or from:
Example
Consider the system:
We can apply our test, selecting an arbitrarily large finite constant M, and an arbitrary input x such that M>x>-M
As M approaches infinity (but does not reach infinity), we can show that:
And:
So now, we can write out our inequality:
And this inequality should be satisfied for all possible values of x. However, we can see that when x is zero, we have the following:
Which means that x is between -M and M, but the value yx is not between y-M and yM. Therefore, this system is not stable.
Poles and Stability
When the poles of the closed-loop transfer function of a given system are located in the right-half of the S-plane (RHP), the system becomes unstable. When the poles of the system are located in the left-half plane (LHP) and the system is not improper, the system is shown to be stable. A number of tests deal with this particular facet of stability: The Routh-Hurwitz Criteria, the Root-Locus, and the Nyquist Stability Criteria all test whether there are poles of the transfer function in the RHP. We will learn about all these tests in the upcoming chapters.
If the system is a multivariable, or a MIMO system, then the system is stable if and only if every pole of every transfer function in the transfer function matrix has a negative real part and every transfer function in the transfer function matrix is not improper. For these systems, it is possible to use the Routh-Hurwitz, Root Locus, and Nyquist methods described later, but these methods must be performed once for each individual transfer function in the transfer function matrix.
Poles and Eigenvalues
Every pole of G(s) is an eigenvalue of the system matrix A. However, not every eigenvalue of A is a pole of G(s).
The poles of the transfer function, and the eigenvalues of the system matrix A are related. In fact, we can say that the eigenvalues of the system matrix A are the poles of the transfer function of the system. In this way, if we have the eigenvalues of a system in the state-space domain, we can use the Routh-Hurwitz, and Root Locus methods as if we had our system represented by a transfer function instead.
On a related note, eigenvalues and all methods and mathematical techniques that use eigenvalues to determine system stability only work with time-invariant systems. In systems which are time-variant, the methods using eigenvalues to determine system stability fail.
Transfer Functions Revisited
We are going to have a brief refesher here about transfer functions, because several of the later chapters will use transfer functions for analyzing system stability.
Let us remember our generalized feedback-loop transfer function, with a gain element of K, a forward path Gp(s), and a feedback of Gb(s). We write the transfer function for this system as:
Where is the closed-loop transfer function, and is the open-loop transfer function. Again, we define the open-loop transfer function as the product of the forward path and the feedback elements, as such:
- <---Note this definition now contradicts the updated definition in the Feedback Loops section.
Now, we can define F(s) to be the characteristic equation. F(s) is simply the denominator of the closed-loop transfer function, and can be defined as such:
[Characteristic Equation]
We can say conclusively that the roots of the characteristic equation are the poles of the transfer function. Now, we know a few simple facts:
- The locations of the poles of the closed-loop transfer function determine if the system is stable or not
- The zeros of the characteristic equation are the poles of the closed-loop transfer function.
- The characteristic equation is always a simpler equation than the closed-loop transfer function.
These functions combined show us that we can focus our attention on the characteristic equation, and find the roots of that equation.
State-Space and Stability
As we have discussed earlier, the system is stable if the eigenvalues of the system matrix A have negative real parts. However, there are other stability issues that we can analyze, such as whether a system is uniformly stable, asymptotically stable, or otherwise. We will discuss all these topics in a later chapter.
Marginal Stability
When the poles of the system in the complex s-domain exist on the imaginary axis (the vertical axis), or when the eigenvalues of the system matrix are imaginary (no real part), the system exhibits oscillatory characteristics, and is said to be marginally stable. A marginally stable system may become unstable under certain circumstances, and may be perfectly stable under other circumstances. It is impossible to tell by inspection whether a marginally stable system will become unstable or not.
We will discuss marginal stability more in the following chapters.
Discrete Time Stability
Discrete-Time Stability
The stability analysis of a discrete-time or digital system is similar to the analysis for a continuous time system. However, there are enough differences that it warrants a separate chapter.
Input-Output Stability
Uniform Stability
An LTI causal system is uniformly BIBO stable if there exists a positive constant L such that the following conditions:
imply that
Impulse Response Matrix
We can define the impulse response matrix of a discrete-time system as:
[Impulse Response Matrix]
Or, in the general time-varying case:
A digital system is BIBO stable if and only if there exists a positive constant L such that for all non-negative k:
Stability of Transfer Function
A MIMO discrete-time system is BIBO stable if and only if every pole of every transfer function in the transfer function matrix has a magnitude less than 1. All poles of all transfer functions must exist inside the unit circle on the Z plane.
Lyapunov Stability
There is a discrete version of the Lyapunov stability theorem that applies to digital systems. Given the discrete Lyapunov equation:
[Digital Lypapunov Equation]
We can use this version of the Lyapunov equation to define a condition for stability in discrete-time systems:
- Lyapunov Stability Theorem (Digital Systems)
- A digital system with the system matrix A is asymptotically stable if and only if there exists a unique matrix M that satisfies the Lyapunov Equation for every positive definite matrix N.
Poles and Eigenvalues
Every pole of G(z) is an eigenvalue of the system matrix A. Not every eigenvalue of A is a pole of G(z). Like the poles of the transfer function, all the eigenvalues of the system matrix must have magnitudes less than 1. Mathematically:
If the magnitude of the eigenvalues of the system matrix A, or the poles of the transfer functions are greater than 1, the system is unstable.
Finite Wordlengths
Digital computer systems have an inherent problem because implementable computer systems have finite wordlengths to deal with. Some of the issues are:
- Real numbers can only be represented with a finite precision. Typically, a computer system can only accurately represent a number to a finite number of decimal points.
- Because of the fact above, computer systems with feedback can compound errors with each program iteration. Small errors in one step of an algorithm can lead to large errors later in the program.
- Integer numbers in computer systems have finite lengths. Because of this, integer numbers will either roll-over, or saturate, depending on the design of the computer system. Both situations can create inaccurate results.
State-Space Stability
State-Space Stability
If a system is represented in the state-space domain, it doesn't make sense to convert that system to a transfer function representation (or even a transfer matrix representation) in an attempt to use any of the previous stability methods. Luckily, there are other analysis methods that can be used with the state-space representation to determine if a system is stable or not. First, let us first introduce the notion of unstability:
- Unstable
- A system is said to be unstable if the system response approaches infinity as time approaches infinity. If our system is G(t), then, we can say a system is unstable if:
Also, a key concept when we are talking about stability of systems is the concept of an equilibrium point:
- Equilibrium Point
- Given a system f such that:
A particular state xe is called an equilibrium point if
for all time t in the interval , where t0 is the starting time of the system.
The definitions below typically require that the equilibrium point be zero. If we have an equilibrium point xe = a, then we can use the following change of variables to make the equilibrium point zero:
We will also see below that a system's stability is defined in terms of an equilibrium point. Related to the concept of an equilibrium point is the notion of a zero point:
- Zero State
- A state xz is a zero state if xz = 0. A zero state may or may not be an equilibrium point.
Stability Definitions
The equilibrium x = 0 of the system is stable if and only if the solutions of the zero-input state equation are bounded. Equivalently, x = 0 is a stable equilibrium if and only if for every initial time t0, there exists an associated finite constant k(t0) such that:
Where sup is the supremum, or "maximum" value of the equation. The maximum value of this equation must never exceed the arbitrary finite constant k (and therefore it may not be infinite at any point).
- Uniform Stability
- The system is defined to be uniformly stable if it is stable for all initial values of t0:
Uniform stability is a more general, and more powerful form of stability than was previously provided.
- Asymptotic Stability
- A system is defined to be asymptotically stable if:
A time-invariant system is asymptotically stable if all the eigenvalues of the system matrix A have negative real parts. If a system is asymptotically stable, it is also BIBO stable. However the inverse is not true: A system that is BIBO stable might not be asymptotically stable.
- Uniform Asymptotic Stability
- A system is defined to be uniformly asymptotically stable if the system is asymptotically stable for all values of t0.
- Exponential Stability
- A system is defined to be exponentially stable if the system response decays exponentially towards zero as time approaches infinity.
For linear systems, uniform asymptotic stability is the same as exponential stability. This is not the case with non-linear systems.
Marginal Stability
Here we will discuss some rules concerning systems that are marginally stable. Because we are discussing eigenvalues and eigenvectors, these theorems only apply to time-invariant systems.
- A time-invariant system is marginally stable if and only if all the eigenvalues of the system matrix A are zero or have negative real parts, and those with zero real parts are simple roots of the minimal polynomial of A.
- The equilibrium x = 0 of the state equation is uniformly stable if all eigenvalues of A have non-positive real parts, and there is a complete set of distinct eigenvectors associated with the eigenvalues with zero real parts.
- The equilibrium x = 0 of the state equation is exponentially stable if and only if all eigenvalues of the system matrix A have negative real parts.
Eigenvalues and Poles
A Linearly Time Invariant (LTI) system is stable (asymptotically stable, see above) if all the eigenvalues of A have negative real parts. Consider the following state equation:
We can take the Laplace Transform of both sides of this equation, using initial conditions of x0 = 0:
Subtract AX(s) from both sides:
Assuming (sI - A) is nonsingular, we can multiply both sides by the inverse:
Now, if we remember our formula for finding the matrix inverse from the adjoint matrix:
We can use that definition here:
Let's look at the denominator (which we will now call D(s)) more closely. To be stable, the following condition must be true:
And if we substitute λ for s, we see that this is actually the characteristic equation of matrix A! This means that the values for s that satisfy the equation (the poles of our transfer function) are precisely the eigenvalues of matrix A. In the S domain, it is required that all the poles of the system be located in the left-half plane, and therefore all the eigenvalues of A must have negative real parts.
Impulse Response Matrix
We can define the Impulse response matrix, G(t, τ) in order to define further tests for stability:
[Impulse Response Matrix]
The system is uniformly stable if and only if there exists a finite positive constant L such that for all time t and all initial conditions t0 with the following integral is satisfied:
In other words, the above integral must have a finite value, or the system is not uniformly stable.
In the time-invariant case, the impulse response matrix reduces to:
In a time-invariant system, we can use the impulse response matrix to determine if the system is uniformly BIBO stable by taking a similar integral:
Where L is a finite constant.
Positive Definiteness
These terms are important, and will be used in further discussions on this topic.
- f(x) is positive definite if f(x) > 0 for all x.
- f(x) is positive semi-definite if for all x, and f(x) = 0 only if x = 0.
- f(x) is negative definite if f(x) < 0 for all x.
- f(x) is negative semi-definite if for all x, and f(x) = 0 only if x = 0.
A Hermitian matrix X is positive definite if all its principle minors are positive. Also, a matrix X is positive definite if all its eigenvalues have positive real parts. These two methods may be used interchangeably.
Positive definiteness is a very important concept. So much so that the Lyapunov stability test depends on it. The other categorizations are not as important, but are included here for completeness.
Lyapunov Stability
Lyapunov's Equation
For linear systems, we can use the Lyapunov Equation, below, to determine if a system is stable. We will state the Lyapunov Equation first, and then state the Lyapunov Stability Theorem.
[Lyapunov Equation]
Where A is the system matrix, and M and N are p × p square matrices.
- Lyapunov Stability Theorem
- An LTI system is stable if there exists a matrix M that satisfies the Lyapunov Equation where N is an arbitrary positive definite matrix, and M is a unique positive definite matrix.
Notice that for the Lyapunov Equation to be satisfied, the matrices must be compatible sizes. In fact, matrices A, M, and N must all be square matrices of equal size. Alternatively, we can write:
- Lyapunov Stability Theorem (alternate)
- If all the eigenvalues of the system matrix A have negative real parts, then the Lyapunov Equation has a unique solution M for every positive definite matrix N, and the solution can be calculated by:
If the matrix M can be calculated in this manner, the system is asymptotically stable.
Controllers and Compensators
There are a number of preexisting devices for use in system control, such as lead and lag compensators, and powerful PID controllers. PID controllers are so powerful that many control engineers may use no other method of system control! The chapters in this section will discuss some of the common types of system compensators and controllers.
Controllability and Observability
System Interaction
In the world of control engineering, there are a slew of systems available that need to be controlled. The task of a control engineer is to design controller and compensator units to interact with these pre-existing systems. However, some systems simply cannot be controlled (or, more often, cannot be controlled in specific ways). The concept of controllability refers to the ability of a controller to arbitrarily alter the functionality of the system plant.
The state-variable of a system, x, represents the internal workings of the system that can be separate from the regular input-output relationship of the system. This also needs to be measured, or observed. The term observability describes whether the internal state variables of the system can be externally measured.
Controllability
Complete state controllability (or simply controllability if no other context is given) describes the ability of an external input to move the internal state of a system from any initial state to any other final state in a finite time interval
We will start off with the definitions of the term controllability, and the related terms reachability and stabilizability.
- Controllability
- A system with internal state vector x is called controllable if and only if the system states can be changed by changing the system input.
- Reachability
- A particular state x1 is called reachable if there exists an input that transfers the state of the system from the initial state x0 to x1 in some finite time interval [t0, t).
- Stabilizability
- A system is Stabilizable if all states that cannot be reached decay to zero asymptotically.
We can also write out the definition of reachability more precisely:
A state x1 is called reachable at time t1 if for some finite initial time t0 there exists an input u(t) that transfers the state x(t) from the origin at t0 to x1.
A system is reachable at time t1 if every state x1 in the state-space is reachable at time t1.
Similarly, we can more precisely define the concept of controllability:
A state x0 is controllable at time t0 if for some finite time t1 there exists an input u(t) that transfers the state x(t) from x0 to the origin at time t1.
A system is called controllable at time t0 if every state x0 in the state-space is controllable.
Controllability Matrix
For LTI (linear time-invariant) systems, a system is reachable if and only if its controllability matrix, ζ, has a full row rank of p, where p is the dimension of the matrix A, and p × q is the dimension of matrix B.
[Controllability Matrix]
A system is controllable or "Controllable to the origin" when any state x1 can be driven to the zero state x = 0 in a finite number of steps.
A system is controllable when the rank of the system matrix A is p, and the rank of the controllability matrix is equal to:
If the second equation is not satisfied, the system is not .
MATLAB allows one to easily create the controllability matrix with the ctrb command. To create the controllability matrix simply type
where A and B are mentioned above. Then in order to determine if the system is controllable or not one can use the rank command to determine if it has full rank.
If
Then controllability does not imply reachability.
- Reachability always implies controllability.
- Controllability only implies reachability when the state transition matrix is nonsingular.
Determining Reachability
There are four methods that can be used to determine if a system is reachable or not:
- If the p rows of are linearly independent over the field of complex numbers. That is, if the rank of the product of those two matrices is equal to p for all values of t and τ
- If the rank of the controllability matrix is the same as the rank of the system matrix A.
- If the rank of for all eigenvalues λ of the matrix A.
- If the rank of the reachability gramian (described below) is equal to the rank of the system matrix A.
Each one of these conditions is both necessary and sufficient. If any one test fails, all the tests will fail, and the system is not reachable. If any test is positive, then all the tests will be positive, and the system is reachable.
Gramians
Gramians are complicated mathematical functions that can be used to determine specific things about a system. For instance, we can use gramians to determine whether a system is controllable or reachable. Gramians, because they are more complicated than other methods, are typically only used when other methods of analyzing a system fail (or are too difficult).
All the gramians presented on this page are all matrices with dimension p × p (the same size as the system matrix A).
All the gramians presented here will be described using the general case of Linear time-variant systems. To change these into LTI (time-invariant equations), the following substitutions can be used:
Where we are using the notation X' to denote the transpose of a matrix X (as opposed to the traditional notation XT).
Reachability Gramian
We can define the reachability gramian as the following integral:
[Reachability Gramian]
The system is reachable if the rank of the reachability gramian is the same as the rank of the system matrix:
<chemistry>/control{range}
Controllability Gramian
We can define the controllability gramian of a system (A, B) as:
[Controllability Gramian]
The system is controllable if the rank of the controllability gramian is the same as the rank of the system matrix:
If the system is time-invariant, there are two important points to be made. First, the reachability gramian and the controllability gramian reduce to be the same equation. Therefore, for LTI systems, if we have found one gramian, then we automatically know both gramians. Second, the controllability gramian can also be found as the solution to the following Lyapunov equation:
Many software packages, notably MATLAB, have functions to solve the Lyapunov equation. By using this last relation, we can also solve for the controllability gramian using these existing functions.
Observability
The state-variables of a system might not be able to be measured for any of the following reasons:
- The location of the particular state variable might not be physically accessible (a capacitor or a spring, for instance).
- There are no appropriate instruments to measure the state variable, or the state-variable might be measured in units for which there does not exist any measurement device.
- The state-variable is a derived "dummy" variable that has no physical meaning.
If things cannot be directly observed, for any of the reasons above, it can be necessary to calculate or estimate the values of the internal state variables, using only the input/output relation of the system, and the output history of the system from the starting time. In other words, we must ask whether or not it is possible to determine what the inside of the system (the internal system states) is like, by only observing the outside performance of the system (input and output)? We can provide the following formal definition of mathematical observability:
- Observability
- A system with an initial state, is observable if and only if the value of the initial state can be determined from the system output y(t) that has been observed through the time interval . If the initial state cannot be so determined, the system is unobservable.
- Complete Observability
- A system is said to be completely observable if all the possible initial states of the system can be observed. Systems that fail this criteria are said to be unobservable.
- Detectability
- A system is Detectable if all states that cannot be observed decay to zero asymptotically.
- Constructability
- A system is constructable if the present state of the system can be determined from the present and past outputs and inputs to the system. If a system is observable, then it is also constructable. The relationship does not work the other way around.
A system state xi is unobservable at a given time ti if the zero-input response of the system is zero for all time t. If a system is observable, then the only state that produces a zero output for all time is the zero state. We can use this concept to define the term state-observability.
- State-Observability
- A system is completely state-observable at time t0 or the pair (A, C) is observable at t0 if the only state that is unobservable at t0 is the zero state x = 0.
Constructability
A state x is unconstructable at a time t1 if for every finite time t < t1 the zero input response of the system is zero for all time t.
A system is completely state constructable at time t1 if the only state x that is unconstructable at t0 is x = 0.
If a system is observable at an initial time t0, then it is constructable at some time t > t0, if it is constructable at t1.
Observability Matrix
The observability of the system is dependent only on the system states and the system output, so we can simplify our state equations to remove the input terms:
Matrix Dimensions:
A: p × p
B: p × q
C: r × p
D: r × q
Therefore, we can show that the observability of the system is dependent only on the coefficient matrices A and C. We can show precisely how to determine whether a system is observable, using only these two matrices. If we have the observability matrix Q:
[Observability Matrix]
we can show that the system is observable if and only if the Q matrix has a rank of p. Notice that the Q matrix has the dimensions pr × p.
MATLAB allows one to easily create the observability matrix with the obsv command. To create the observability matrix simply type
- Q=obsv(A,C)
where A and C are mentioned above. Then in order to determine if the system is observable or not one can use the rank command to determine if it has full rank.
Observability Gramian
We can define an observability gramian as:
[Observability Gramian]
A system is completely state observable at time t0 < t < t1 if and only if the rank of the observability gramian is equal to the size p of the system matrix A.
If the system (A, B, C, D) is time-invariant, we can construct the observability gramian as the solution to the Lyapunov equation:
Constructability Gramian
We can define a constructability gramian as:
[Constructability Gramian]
A system is completely state observable at an initial time t0 if and only if there exists a finite t1 such that:
Notice that the constructability and observability gramians are very similar, and typically they can both be calculated at the same time, only substituting in different values into the state-transition matrix.
Duality Principle
The concepts of controllability and observability are very similar. In fact, there is a concrete relationship between the two. We can say that a system (A, B) is controllable if and only if the system (A', C, B', D) is observable. This fact can be proven by plugging A' in for A, and B' in for C into the observability Gramian. The resulting equation will exactly mirror the formula for the controllability gramian, implying that the two results are the same.
System Specifications
System Specification
There are a number of different specifications that might need to be met by a new system design. In this chapter we will talk about some of the specifications that systems use, and some of the ways that engineers analyze and quantify technical systems.
Steady-State Accuracy
Sensitivity
The sensitivity of a system is a parameter that is specified in terms of a given output and a given input. The sensitivity measures how much change is caused in the output by small changes to the reference input. Sensitive systems have very large changes in output in response to small changes in the input. The sensitivity of system H to input X is denoted as:
Disturbance Rejection
All physically-realized systems have to deal with a certain amount of noise and disturbance. The ability of a system to reject the noise is known as the disturbance rejection of the system.
Control Effort
The control effort is the amount of energy or power necessary for the controller to perform its duty.
Controllers
Controllers
There are a number of different standard types of control systems that have been studied extensively. These controllers, specifically the P, PD, PI, and PID controllers are very common in the production of physical systems, but as we will see they each carry several drawbacks.
Proportional Controllers

Proportional controllers are simply gain values. These are essentially multiplicative coefficients, usually denoted with a K. A P controller can only force the system poles to a spot on the system's root locus. A P controller cannot be used for arbitrary pole placement.
We refer to this kind of controller by a number of different names: proportional controller, gain, and zeroth-order controller.
Derivative Controllers

In the Laplace domain, we can show the derivative of a signal using the following notation:
Since most systems that we are considering have zero initial condition, this simplifies to:
The derivative controllers are implemented to account for future values, by taking the derivative, and controlling based on where the signal is going to be in the future. Derivative controllers should be used with care, because even small amount of high-frequency noise can cause very large derivatives, which appear like amplified noise. Also, derivative controllers are difficult to implement perfectly in hardware or software, so frequently solutions involving only integral controllers or proportional controllers are preferred over using derivative controllers.
Notice that derivative controllers are not proper systems, in that the order of the numerator of the system is greater than the order of the denominator of the system. This quality of being a non-proper system also makes certain mathematical analysis of these systems difficult.
Z-Domain Derivatives
We won't derive this equation here, but suffice it to say that the following equation in the Z-domain performs the same function as the Laplace-domain derivative:
Where T is the sampling time of the signal.
Integral Controllers

To implemenent an Integral in a Laplace domain transfer function, we use the following:
Integral controllers of this type add up the area under the curve for past time. In this manner, a PI controller (and eventually a PID) can take account of the past performance of the controller, and correct based on past errors.
Z-Domain Integral
The integral controller can be implemented in the Z domain using the following equation:
PID Controllers

PID controllers are combinations of the proportional, derivative, and integral controllers. Because of this, PID controllers have large amounts of flexibility. We will see below that there are definite limites on PID control.
PID Transfer Function
The transfer function for a standard PID controller is an addition of the Proportional, the Integral, and the Differential controller transfer functions (hence the name, PID). Also, we give each term a gain constant, to control the weight that each factor has on the final output:
[PID]
Notice that we can write the transfer function of a PID controller in a slightly different way:
This form of the equation will be especially useful to us when we look at polynomial design.
PID Signal flow diagram

PID Tuning
The process of selecting the various coefficient values to make a PID controller perform correctly is called PID Tuning. There are a number of different methods for determining these values:[1]
1) Direct Synthesis (DS) method
2) Internal Model Control (IMC) method
3) Controller tuning relations
4) Frequency response techniques
5) Computer simulation
6) On-line tuning after the control system is installed
7)Trial and error
Notes:
- ↑ Seborg, Dale E.; Edgar, Thomas F.; Mellichamp, Duncan A. (2003). Process Dynamics and Control, Second Edition. John Wiley & Sons,Inc. ISBN 0471000779
Digital PID
In the Z domain, the PID controller has the following transfer function:
[Digital PID]
And we can convert this into a canonical equation by manipulating the above equation to obtain:
Where:
Once we have the Z-domain transfer function of the PID controller, we can convert it into the digital time domain:
And finally, from this difference equation, we can create a digital filter structure to implement the PID.
For more information about digital filter structures, see Digital Signal Processing |
Bang-Bang Controllers
Despite the low-brow sounding name of the Bang-Bang controller, it is a very useful tool that is only really available using digital methods. A better name perhaps for a bang-bang controller is an on/off controller, where a digital system makes decisions based on target and threshold values, and decides whether to turn the controller on and off. Bang-bang controllers are a non-linear style of control.
Consider the example of a household furnace. The oil in a furnace burns at a specific temperature—it can't burn hotter or cooler. To control the temperature in your house then, the thermostat control unit decides when to turn the furnace on, and when to turn the furnace off. This on/off control scheme is a bang-bang controller.
Compensation
There are a number of different compensation units that can be employed to help fix certain system metrics that are outside of a proper operating range. Most commonly, the phase characteristics are in need of compensation, especially if the magnitude response is to remain constant. There are four major types of compensation 1. Lead compensation 2. Lag compensation 3. Lead-lag compensation 4. Lag-lead compensation
Phase Compensation
Occasionally, it is necessary to alter the phase characteristics of a given system, without altering the magnitude characteristics. To do this, we need to alter the frequency response in such a way that the phase response is altered, but the magnitude response is not altered. To do this, we implement a special variety of controllers known as phase compensators. They are called compensators because they help to improve the phase response of the system.
There are two general types of compensators: Lead Compensators, and Lag Compensators. If we combine the two types, we can get a special Lag-lead Compensator system.(lead-lag system is not practically realisable).
When designing and implementing a phase compensator, it is important to analyze the effects on the gain and phase margins of the system, to ensure that compensation doesn't cause the system to become unstable. phase lead compensation:- 1 it is same as addition of zero to open loop TF since from pole zero point of view zero is nearer to origin than pole hence effect of zero dominant.
Phase Lead
The transfer function for a lead-compensator is as follows:
[Lead Compensator]
To make the compensator work correctly, the following property must be satisfied:
And both the pole and zero location should be close to the origin, in the LHP. Because there is only one pole and one zero, they both should be located on the real axis.
Phase lead compensators help to shift the poles of the transfer function to the left, which is beneficial for stability purposes.
Phase Lag
The transfer function for a lag compensator is the same as the lead-compensator, and is as follows:
[Lag Compensator]
However, in the lag compensator, the location of the pole and zero should be swapped:
Both the pole and the zero should be close to the origin, on the real axis.
The Phase lag compensator helps to improve the steady-state error of the system. The poles of the lag compensator should be very close together to help prevent the poles of the system from shifting right, and therefore reducing system stability.
Phase Lag-lead
The transfer function of a Lag-lead compensator is simply a multiplication of the lead and lag compensator transfer functions, and is given as:
[Lag-lead Compensator]
Where typically the following relationship must hold true:
External links
- Standard Controller Forms on ControlTheoryPro.com
- PID Control on ControlTheoryPro.com
- PI Control on ControlTheoryPro.com
Compensators
Controllers
There are a number of different standard types of control systems that have been studied extensively. These controllers, specifically the P, PD, PI, and PID controllers are very common in the production of physical systems, but as we will see they each carry several drawbacks.
Proportional Controllers

Proportional controllers are simply gain values. These are essentially multiplicative coefficients, usually denoted with a K. A P controller can only force the system poles to a spot on the system's root locus. A P controller cannot be used for arbitrary pole placement.
We refer to this kind of controller by a number of different names: proportional controller, gain, and zeroth-order controller.
Derivative Controllers

In the Laplace domain, we can show the derivative of a signal using the following notation:
Since most systems that we are considering have zero initial condition, this simplifies to:
The derivative controllers are implemented to account for future values, by taking the derivative, and controlling based on where the signal is going to be in the future. Derivative controllers should be used with care, because even small amount of high-frequency noise can cause very large derivatives, which appear like amplified noise. Also, derivative controllers are difficult to implement perfectly in hardware or software, so frequently solutions involving only integral controllers or proportional controllers are preferred over using derivative controllers.
Notice that derivative controllers are not proper systems, in that the order of the numerator of the system is greater than the order of the denominator of the system. This quality of being a non-proper system also makes certain mathematical analysis of these systems difficult.
Z-Domain Derivatives
We won't derive this equation here, but suffice it to say that the following equation in the Z-domain performs the same function as the Laplace-domain derivative:
Where T is the sampling time of the signal.
Integral Controllers

To implemenent an Integral in a Laplace domain transfer function, we use the following:
Integral controllers of this type add up the area under the curve for past time. In this manner, a PI controller (and eventually a PID) can take account of the past performance of the controller, and correct based on past errors.
Z-Domain Integral
The integral controller can be implemented in the Z domain using the following equation:
PID Controllers

PID controllers are combinations of the proportional, derivative, and integral controllers. Because of this, PID controllers have large amounts of flexibility. We will see below that there are definite limites on PID control.
PID Transfer Function
The transfer function for a standard PID controller is an addition of the Proportional, the Integral, and the Differential controller transfer functions (hence the name, PID). Also, we give each term a gain constant, to control the weight that each factor has on the final output:
[PID]
Notice that we can write the transfer function of a PID controller in a slightly different way:
This form of the equation will be especially useful to us when we look at polynomial design.
PID Signal flow diagram

PID Tuning
The process of selecting the various coefficient values to make a PID controller perform correctly is called PID Tuning. There are a number of different methods for determining these values:[1]
1) Direct Synthesis (DS) method
2) Internal Model Control (IMC) method
3) Controller tuning relations
4) Frequency response techniques
5) Computer simulation
6) On-line tuning after the control system is installed
7)Trial and error
Notes:
- ↑ Seborg, Dale E.; Edgar, Thomas F.; Mellichamp, Duncan A. (2003). Process Dynamics and Control, Second Edition. John Wiley & Sons,Inc. ISBN 0471000779
Digital PID
In the Z domain, the PID controller has the following transfer function:
[Digital PID]
And we can convert this into a canonical equation by manipulating the above equation to obtain:
Where:
Once we have the Z-domain transfer function of the PID controller, we can convert it into the digital time domain:
And finally, from this difference equation, we can create a digital filter structure to implement the PID.
For more information about digital filter structures, see Digital Signal Processing |
Bang-Bang Controllers
Despite the low-brow sounding name of the Bang-Bang controller, it is a very useful tool that is only really available using digital methods. A better name perhaps for a bang-bang controller is an on/off controller, where a digital system makes decisions based on target and threshold values, and decides whether to turn the controller on and off. Bang-bang controllers are a non-linear style of control.
Consider the example of a household furnace. The oil in a furnace burns at a specific temperature—it can't burn hotter or cooler. To control the temperature in your house then, the thermostat control unit decides when to turn the furnace on, and when to turn the furnace off. This on/off control scheme is a bang-bang controller.
Compensation
There are a number of different compensation units that can be employed to help fix certain system metrics that are outside of a proper operating range. Most commonly, the phase characteristics are in need of compensation, especially if the magnitude response is to remain constant. There are four major types of compensation 1. Lead compensation 2. Lag compensation 3. Lead-lag compensation 4. Lag-lead compensation
Phase Compensation
Occasionally, it is necessary to alter the phase characteristics of a given system, without altering the magnitude characteristics. To do this, we need to alter the frequency response in such a way that the phase response is altered, but the magnitude response is not altered. To do this, we implement a special variety of controllers known as phase compensators. They are called compensators because they help to improve the phase response of the system.
There are two general types of compensators: Lead Compensators, and Lag Compensators. If we combine the two types, we can get a special Lag-lead Compensator system.(lead-lag system is not practically realisable).
When designing and implementing a phase compensator, it is important to analyze the effects on the gain and phase margins of the system, to ensure that compensation doesn't cause the system to become unstable. phase lead compensation:- 1 it is same as addition of zero to open loop TF since from pole zero point of view zero is nearer to origin than pole hence effect of zero dominant.
Phase Lead
The transfer function for a lead-compensator is as follows:
[Lead Compensator]
To make the compensator work correctly, the following property must be satisfied:
And both the pole and zero location should be close to the origin, in the LHP. Because there is only one pole and one zero, they both should be located on the real axis.
Phase lead compensators help to shift the poles of the transfer function to the left, which is beneficial for stability purposes.
Phase Lag
The transfer function for a lag compensator is the same as the lead-compensator, and is as follows:
[Lag Compensator]
However, in the lag compensator, the location of the pole and zero should be swapped:
Both the pole and the zero should be close to the origin, on the real axis.
The Phase lag compensator helps to improve the steady-state error of the system. The poles of the lag compensator should be very close together to help prevent the poles of the system from shifting right, and therefore reducing system stability.
Phase Lag-lead
The transfer function of a Lag-lead compensator is simply a multiplication of the lead and lag compensator transfer functions, and is given as:
[Lag-lead Compensator]
Where typically the following relationship must hold true:
External links
- Standard Controller Forms on ControlTheoryPro.com
- PID Control on ControlTheoryPro.com
- PI Control on ControlTheoryPro.com
Advanced Topics
The following chapters are going to begin exploration into more advanced topics, such as nonlinear systems, and noise-driven systems. Currently, this book does not cover these subjects or any other advanced topics with any measure of completeness.
Nonlinear Systems
Nonlinear General Solution
A nonlinear system, in general, can be defined as follows:
Where f is a nonlinear function of the time, the system state, and the initial conditions. If the initial conditions are known, we can simplify this as:
The general solution of this equation (or the most general form of a solution that we can state without knowing the form of f) is given by:
and we can prove that this is the general solution to the above equation because when we differentiate both sides we get the origin equation.
Iteration Method
The general solution to a nonlinear system can be found through a method of infinite iteration. We will define xn as being an iterative family of indexed variables. We can define them recursively as such:
We can show that the following relationship is true:
The xn series of equations will converge on the solution to the equation as n approaches infinity.
Types of Nonlinearities
Nonlinearities can be of two types:
- Intentional non-linearity: The non-linear elements that are added into a system. Eg: Relay
- Incidental non-linearity: The non-linear behavior that is already present in the system. Eg: Saturation
Linearization
Nonlinear systems are difficult to analyze, and for that reason one of the best methods for analyzing those systems is to find a linear approximation to the system. Frequently, such approximations are only good for certain operating ranges, and are not valid beyond certain bounds. The process of finding a suitable linear approximation to a nonlinear system is known as linearization.

This image shows a linear approximation (dashed line) to a non-linear system response (solid line). This linear approximation, like most, is accurate within a certain range, but becomes more inaccurate outside that range. Notice how the curve and the linear approximation diverge towards the right of the graph.
Noise Driven Systems
Control Systems/Noise-Driven Systems
Appendicies
Appendix 1: Physical Models
Appendix 2: System Representations
Appendix 3: Matrix Operations
Appendix 4: MatLab
Appendix: Physical Models
Physical Models
This page will serve as a refresher for various different engineering disciplines on how physical devices are modeled. Models will be displayed in both time-domain and Laplace-domain input/output characteristics. The only information that is going to be displayed here will be the ones that are contributed by knowledgeable contributors.
Electrical Systems
Circuit Theory
Electronics
Component Time-Domain Laplace Fourier Resistor R R R Capacitor Inductor
Mechanical Systems
Civil/Construction Systems
Chemical Systems
System Representations
System Representations
This is a table of times when it is appropriate to use each different type of system representation:
| Properties | State-Space Equations |
Transfer Function |
Transfer Matrix |
|---|---|---|---|
| Linear, Distributed | no | no | no |
| Linear, Lumped | yes | no | no |
| Linear, Time-Invariant, Distributed | no | yes | no |
| Linear, Time-Invariant, Lumped | yes | yes | yes |
General Description
These are the general external system descriptions. y is the system output, h is the system response characteristic, and x is the system input. In the time-variant cases, the general description is also known as the convolution description.
| General Description | |
|---|---|
| Time-Invariant, Non-causal | |
| Time-Invariant, Causal | |
| Time-Variant, Non-Causal | |
| Time-Variant, Causal | |
State-Space Equations
These are the state-space representations for a system. y is the system output, x is the internal system state, and u is the system input. The matrices A, B, C, and D are coefficient matrices.
[Analog State Equations]
| State-Space Equations | |
|---|---|
| Time-Invariant |
|
| Time-Variant |
|
These are the digital versions of the equations listed above. All the variables have the same meanings, except that the systems are digital.
[Digital State Equations]
| State-Space Equations | |
|---|---|
| Time-Invariant |
|
| Time-Variant |
|
Transfer Functions
These are the transfer function descriptions, obtained by using the Laplace Transform or the Z-Transform on the general system descriptions listed above. Y is the system output, H is the system transfer function, and X is the system input.
[Analog Transfer Function]
| Transfer Function | |
|---|---|
[Digital Transfer Function]
| Transfer Function | |
|---|---|
Transfer Matrix
This is the transfer matrix system description. This representation can be obtained by taking the Laplace or Z transforms of the state-space equations. In the SISO case, these equations reduce to the transfer function representations listed above. In the MIMO case, Y is the vector of system outputs, X is the vector of system inputs, and H is the transfer matrix that relates each input X to each output Y.
[Analog Transfer Matrix]
| Transfer Matrix | |
|---|---|
[Digital Transfer Matrix]
| Transfer Matrix | |
|---|---|
Matrix Operations
Laws of Matrix Algebra
Matrices must be compatible sizes in order for an operation to be valid:
- Addition
- Matrices must have the same dimensions (same number of rows, same number of columns). Matrix addition is commutative:
- Multiplication
- Matrices must have the same inner dimensions (the number of columns of the first matrix must equal the number of rows in the second matrix). For instance, if matrix A is n × m, and matrix B is m × k, then we can multiply:
- Where C is an n × k matrix. Matrix multiplication is not commutative:
- Because it is not commutative, the differentiation must be made between "multiplication on the left", and "multiplication on the right".
- Division
- There is no such thing as division in matrix algebra, although multiplication of the matrix inverse performs the same basic function. To find an inverse, a matrix must be nonsingular, and must have a non-zero determinant.
Transpose Matrix
The transpose of a matrix, denoted by:
is the matrix where the rows and columns of X are interchanged. In some instances, the transpose of a matrix is denoted by:
This shorthand notation is used when the superscript T applied to a large number of matrices in a single equation, and the notation would become too crowded otherwise. When this notation is used in the book, derivatives will be denoted explicitly with:
Determinant
The determinant of a matrix it is a scalar value. It is denoted similarly to absolute-value in scalars:
A matrix has an inverse if the matrix is square, and if the determinant of the matrix is non-zero.
Inverse
The inverse of a matrix A, which we will denote here by "B" is any matrix that satisfies the following equation:
Matrices that have such a companion are known as "invertible" matrices, or "non-singular" matrices. Matrices which do not have an inverse that satisfies this equation are called "singular" or "non-invertable".
An inverse can be computed in a number of different ways:
- Append the matrix A with the Identity matrix of the same size. Use row-reductions to make the left side of the matrice an identity. The right side of the appended matrix will then be the inverse:
- The inverse matrix is given by the adjoint matrix divided by the determinant. The adjoint matrix is the transpose of the cofactor matrix.
- The inverse can be calculated from the Cayley-Hamilton Theorem.
Eigenvalues
The eigenvalues of a matrix, denoted by the Greek letter lambda λ, are the solutions to the characteristic equation of the matrix:
Eigenvalues only exist for square matrices. Non-square matrices do not have eigenvalues. If the matrix X is a real matrix, the eigenvalues will either be all real, or else there will be complex conjugate pairs.
Eigenvectors
The eigenvectors of a matrix are the nullspace solutions of the characteristic equation:
There is at least one distinct eigenvector for every distinct eigenvalue. Multiples of an eigenvector are also themselves eigenvectors. However, eigenvalues that are not linearly independent are called "non-distinct" eigenvectors, and can be ignored.
Left-Eigenvectors
Left Eigenvectors are the right-hand nullspace solutions to the characteristic equation:
These are also the rows of the inverse transition matrix.
Generalized Eigenvectors
In the case of repeated eigenvalues, there may not be a complete set of n distinct eigenvectors (right or left eigenvectors) associated with those eigenvalues. Generalized eigenvectors can be generated as follows:
Because generalized eigenvectors are formed in relation to another eigenvector or generalize eigenvectors, they constitute an ordered set, and should not be used outside of this order.
Transformation Matrix
The transformation matrix is the matrix of all the eigenvectors, or the ordered sets of generalized eigenvectors:
The inverse transition matrix is the matrix of the left-eigenvectors:
A matrix can be diagonalized by multiplying by the transition matrix:
Or:
If the matrix has an incomplete set of eigenvectors, and therefore a set of generalized eigenvectors, the matrix cannot be diagonalized, but can be converted into Jordan canonical form:
MATLAB
The MATLAB programming environment was specially designed for matrix algebra and manipulation. The following is a brief refresher about how to manipulate matrices in MATLAB:
- Addition
- To add two matrices together, use a plus sign ("+"):
C = A + B;
- Multiplication
- To multiply two matrices together use an asterisk ("*"):
C = A * B;
- If your matrices are not the correct dimensions, MATLAB will issue an error.
- Transpose
- To find the transpose of a matrix, use the apostrophe (" ' "):
C = A';
- Determinant
- To find the determinant, use the det function:
d = det(A);
- Inverse
- To find the inverse of a matrix, use the function inv:
C = inv(A);
- Eigenvalues and Eigenvectors
- To find the eigenvalues and eigenvectors of a matrix, use the eig command:
[E, V] = eig(A);
- Where E is a square matrix with the eigenvalues of A in the diagonal entries, and V is the matrix comprised of the corresponding eigenvectors. If the eigenvalues are not distinct, the eigenvectors will be repeated. MATLAB will not calculate the generalized eigenvectors.
- Left Eigenvectors
- To find the left eigenvectors, assuming there is a complete set of distinct right-eigenvectors, we can take the inverse of the eigenvector matrix:
[E, V] = eig(A); C = inv(V);
The rows of C will be the left-eigenvectors of the matrix A.
For more information about MATLAB, see the wikibook MATLAB Programming.
Appendix: MatLab
This page would highly benefit from some screenshots of various systems. Users who have MATLAB or Octave available are highly encouraged to produce some screenshots for the systems here. |
MATLAB
MATLAB is a programming language that is specially designed for the manipulation of matrices. Because of its computational power, MATLAB is a tool of choice for many control engineers to design and simulate control systems. This page is going to discuss using MATLAB for control systems design and analysis. MATLAB has a number of plugin modules called "Toolboxes". Nearly all the functions described below are located in the control systems toolbox. If your system has the control systems toolbox installed, you can get more information about the toolbox by typing help control at the MATLAB prompt.
Also, there is an open-source competitor to MATLAB called Octave. Octave is similar to MATLAB, but there are also some differences. This page will focus on MATLAB, but another page could be added to focus on Octave. As of Sept 10th, 2006, all the MATLAB commands listed below have been implemented in GNU octave.
This page will use the {{MATLAB CMD}} template to show MATLAB functions that can be used to perform different tasks.
MATLAB is a copyrighted product produced by The Mathworks. For more information about MATLAB and The Mathworks, see Control Systems/Resources.
Input-Output Isolation
In a MIMO system, typically it can be important to isolate a single input-output pair for analysis. Each input corresponds to a single row in the B matrix, and each output corresponds to a single column in the C matrix. For instance, to isolate the 2nd input and the 3rd output, we can create a system:
sys = ss(A, B(:,2), C(3,:), D);
This page will refer to this technique as "input-output isolation".
Step Response
First, let's take a look at the classical approach, with the following system:
This system can effectively be modeled as two vectors of coefficients, NUM and DEN:
NUM = [5, 10] DEN = [1, 4, 5]
Now, we can use the MATLAB step command to produce the step response to this system:
step(NUM, DEN, t);
Where t is a time vector. If no results on the left-hand side are supplied by you, the step function will automatically produce a graphical plot of the step response. If, however, you use the following format:
[y, x, t] = step(NUM, DEN, t);
Then MATLAB will not produce a plot automatically, and you will have to produce one yourself.
Here is a sample screenshot:
-
Step response
Now, let's look at the modern, state-space approach. If we have the matrices A, B, C and D, we can plug these into the step function, as shown:
step(A, B, C, D);
or, we can optionally include a vector for time, t:
step(A, B, C, D, t);
Again, if we supply results on the left-hand side of the equation, MATLAB will not automatically produce a plot for us.
If we didn't get an automatic plot, and we want to produce our own, we type:
[y, x, t] = step(NUM, DEN, t);
And then we can create a graph using the plot command:
plot(t, y);
y is the output magnitude of the step response, while x is the internal state of the system from the state-space equations:
Classical ↔ Modern
MATLAB contains features that can be used to automatically convert to the state-space representation from the Laplace representation. This function, tf2ss, is used as follows:
[A, B, C, D] = tf2ss(NUM, DEN);
Where NUM and DEN are the coefficient vectors of the numerator and denominator of the transfer function, respectively.
In a similar vein, we can convert from the Laplace domain back to the state-space representation using the ss2tf function, as such:
[NUM, DEN] = ss2tf(A, B, C, D);
Or, if we have more than one input in a vector u, we can write it as follows:
[NUM, DEN] = ss2tf(A, B, C, D, u);
The u parameter must be provided when our system has more than one input, but it does not need to be provided if we have only 1 input. This form of the equation produces a transfer function for each separate input. NUM and DEN become 2-D matricies, with each row being the coefficients for each different input.
z-Domain Digital Filters
Let us now consider a digital system with the following generic transfer function in the Z domain:
Where n(z) and d(z) are the numerator and denominator polynomials of the transfer function, respectively. The filter command can be used to apply an input vector x to the filter. The output, y, can be obtained from the following code:
y = filter(n, d, x);
The word "filter" may be a bit of a misnomer in this case, but the fact remains that this is the method to apply an input to a digital system. Once we have the output magnitude vector, we can plot it using our plot command:
plot(y);
To get the step response of the digital system, we must first create a step function using the ones command:
u = ones(1, N);
Where N is the number of samples that we want to take in our digital system (not to be confused with "n", our numerator coefficient). Once we have produced our unit step function, we can pass this function through our digital filter as such:
y = filter(n, d, u);
And we can plot y:
plot(y);
State-Space Digital Filters
Likewise, we can analyze a digital system in the state-space representation. If we have the following digital state relationship:
We can convert automatically to the pulse response using the ss2tf function, that we used above:
[NUM, DEN] = ss2tf(A, B, C, D);
Then, we can filter it with our prepared unit-step sequence vector, u:
y = filter(num, den, u)
this will give us the step response of the digital system in the state-space representation.
Root Locus Plots
MATLAB supplies a useful, automatic tool for generating the root-locus graph from a transfer function: the rlocus command. In the transfer function domain, or the state space domain respectively, we have the following uses of the function:
rlocus(num, den);
And:
rlocus(A, B, C, D);
These functions will automatically produce root-locus graphs of the system. However, if we provide left-hand parameters:
[r, K] = rlocus(num, den);
Or:
[r, K] = rlocus(A, B, C, D);
The function won't produce a graph automatically, and you will need to produce one yourself. There is also an optional additional parameter for gain, K, that can be supplied:
rlocus(num, den, K);
Or:
rlocus(A, B, C, D, K);
If K is not supplied, MATLAB will supply an automatic gain value for you.
Once we have our values [r, K], we can plot a root locus:
plot(r);
The rlocus command cannot be used with MIMO systems, so if your system is a MIMO system, you must separate out your coefficient matrices to isolate each separate Input-output pair, and graph each individually.
Here is a sample screenshot:
-
root-locus
Digital Root-Locus
Creating a root-locus diagram for a digital system is exactly the same as it is for a continuous system. The only difference is the interpretation of the results, because the stability region for digital systems is different from the stability region for continuous systems. The same rlocus function can be used, in the same manner as is used above.
Bode Plots
MATLAB also offers a number of tools for examining the frequency response characteristics of a system, both using Bode plots, and using Nyquist charts. To construct a Bode plot from a transfer function, we use the following command:
[mag, phase, omega] = bode(NUM, DEN, omega);
Or:
[mag, phase, omega] = bode(A, B, C, D, u, omega);
Where "omega" is the frequency vector where the magnitude and phase response points are analyzed. If we want to convert the magnitude data into decibels, we can use the following conversion:
magdb = 20 * log10(mag);
This conversion should be known well enough by now that it doesn't require explanation.
When talking about Bode plots in decibels, it makes the most sense (and is the most common occurrence) to also use a logarithmic frequency scale. To create such a logarithmic sequence in omega, we use the logspace command, as such:
omega = logspace(a, b, n);
This command produces n points, spaced logarithmicly, from up to .
If we use the bode command without left-hand arguments, MATLAB will produce a graph of the bode phase and magnitude plots automatically.
The bode command, if used with a MIMO system, will use subplots to produce all the input-output relationship graphs on a single plot window. for a system with multiple inputs and multiple outputs, this can become difficult to see clearly. In these cases, it is typically better to separate out your coefficient matrices to isolate each individual input-output pair.
Here is a sample screenshot:
-
Bode plot (Frequency response)
Nyquist Plots
In addition to the bode plots, we can create nyquist charts by using the nyquist command. The nyquist command operates in a similar manner to the bode command (and other commands that we have used so far):
[real, imag, omega] = nyquist(NUM, DEN, omega);
Or:
[real, imag, omega] = nyquist(A, B, C, D, u, omega);
Here, "real" and "imag" are vectors that contain the real and imaginary parts of each point of the nyquist diagram. If we don't supply the right-hand arguments, the nyquist command automatically produces a nyquist plot for us.
Like the bode command, the nyquist command will use subplots to display the input-output relations of MIMO systems on a single plot window. If there are multiple input-output pairs, it can be difficult to see the individual graphs.
Here is a sample screenshot:
-
Nyquist plot
Lyapunov Equations
Controllability
A controllability matrix can be constructed using the ctrb command. The controllability gramian can be constructed using the gram command.
Observability
An observability matrix can be constructed using the command obsv
Empirical Gramians
Empirical gramians can be computed for linear and also nonlinear control systems. The empirical gramian framework emgr allows the computation of the controllability, observability and cross gramian; it is compatible with MATLAB and OCTAVE and does not require the control systems toolbox.
Further reading
- Ogata, Katsuhiko, "Solving Control Engineering Problems with MATLAB", Prentice Hall, New Jersey, 1994. ISBN 0130459070
- MATLAB Programming.
- http://octave.sourceforge.net/
- MATLAB Category on ControlTheoryPro.com
- Empirical Gramian Framework
Glossary
Resources
Licensing
1) Glossary
2) List of Equations
3) Resources and Bibliography
4) Licensing
5) GNU Free Documentation License
Glossary and List of Equations
The following is a listing of some of the most important terms from the book, along with a short definition or description.
A, B, C
- Acceleration Error
- The amount of steady state error of the system when stimulated by a unit parabolic input.
- Acceleration Error Constant
- A system metric that determines that amount of acceleration error in the system.
- Adaptive Control
- A branch of control theory where controller systems are able to change their response characteristics over time, as the input characteristics to the system change.
- Adaptive Gain
- when control gain is varied depending on system state or condition, such as a disturbance
- Additivity
- A system is additive if a sum of inputs results in a sum of outputs.
- Analog System
- A system that is continuous in time and magnitude.
- ARMA
- Autoregressive Moving Average, see [1]
- ATO
- Analog Timed Output. Control loop output is correlated to a timed contact closure.
- A/M
- Auto-Manual. Control modes, where auto typically means output is computer-driven, calculated while manual can be field-driven or merely using a static setpoint.
- Bilinear Transform
- a variant of the Z-transform, see [2]
- Block Diagram
- A visual way to represent a system that displays individual system components as boxes, and connections between systems as arrows.
- Bode Plots
- A set of two graphs, a "magnitude" and a "phase" graph, that are both plotted on log scale paper. The magnitude graph is plotted in decibels versus frequency, and the phase graph is plotted in degrees versus frequency. Used to analyze the frequency characteristics of the system.
- Bounded Input, Bounded Output
- BIBO. If the input to the system is finite, then the output must also be finite. A condition for stability.
- Cascade
- When the output of a control loop is fed to/from another loop.
- Causal
- A system whose output does not depend on future inputs. All physical systems must be causal.
- Classical Approach
- See Classical Controls.
- Classical Controls
- A control methodology that uses the transform domain to analyze and manipulate the Input-Output characteristics of a system.
- Closed Loop
- a controlled system using feedback or feedforward
- Compensator
- A Control System that augments the shortcomings of another system.
- Condition Number
- Conditional Stability
- A system with variable gain is conditionally stable if it is BIBO stable for certain values of gain, but not BIBO stable for other values of gain.
- Continuous-Time
- A system or signal that is defined at all points t.
- Control Rate
- the rate at which control is computed and any appropriate output sent. Lower bound is sample rate.
- Control System
- A system or device that manages the behavior of another system or device.
- Controller
- See Control System.
- Convolution
- A complex operation on functions defined by the integral of the two functions multiplied together, and time-shifted.
- Convolution Integral
- The integral form of the convolution operation.
- CQI
- Control Quality Index, , 1 being ideal.
- CV
- Controlled variable
D, E, F
- Damping Ratio
- A constant that determines the damping properties of a system.
- Deadtime
- time shift between the output change and the related effect (typ. at least one control sample). One sees "Lag" used for this action sometimes.
- Digital
- A system that is both discrete-time, and quantized.
- Direct action
- target output increase is required to bring the process variable (PV) to setpoint (SP) when PV is below SP. Thus, PV increases with output increase directly.
- Discrete magnitude
- See quantized.
- Discrete time
- A system or signal that is only defined at specific points in time.
- Distributed
- A system is distributed if it has both an infinite number of states, and an infinite number of state variables. See Lumped.
- Dynamic
- A system is called dynamic if it doesn't have memory. See Instantaneous, Memory.
- Eigenvalues
- Solutions to the characteristic equation of a matrix. If the matrix is itself a function of time, the eigenvalues might be functions of time. In this case, they are frequently called eigenfunctions.
- Eigenvectors
- The nullspace vectors of the characteristic equation for particular eigenvalues. Used to determine state-transitions, among other things. See [3]
- Euler's Formula
- An equation that relates complex exponentials to complex sinusoids.
- Exponential Weighted Average (EWA)
- Apportions fractional weight to new and existing data to form a working average. Example EWA=0.70*EWA+0.30*latest, see Filtering.
- External Description
- A description of a system that relates the input of the system to the output, without explicitly accounting for the internal states of the system.
- Feedback
- The output of the system is passed through some sort of processing unit H, and that result is fed into the plant as an input.
- Feedforward
- whwn apriori knowledge is used to forecast at least part of the control response.
- Filtering (noise)
- Use of signal smoothing techniques to reject undesirable components like noise. Can be as simple as using exponential weighted averaging on the input.
- Final Value Theorem
- A theorem that allows the steady-state value of a system to be determined from the transfer function.
- FOH
- First order hold
- Frequency Response
- The response of a system to sinusoids of different frequencies. The Fourier Transform of the impulse response.
- Fourier Transform
- An integral transform, similar to the Laplace Transform, that analyzes the frequency characteristics of a system.
See [4]
G, H, I
- Game Theory
- A branch of study that is related to control engineering, and especially optimal control. Multiple competing entities, or "players" attempt to minimize their own cost, and maximize the cost of the opponents.
- Gain
- A constant multiplier in a system that is typically implemented as an amplifier or attenuator. Gain can be changed, but is typically not a function of time. Adaptive control can use time-adaptive gains that change with time.
- General Description
- An external description of a system that relates the system output to the system input, the system response, and a time constant through integration.
- Hendrik Wade Bode
- Electrical Engineer, did work in control theory and communications. Is primarily remembered in control engineering for his introduction of the bode plot.
- Harry Nyquist
- Electrical Engineer, did extensive work in controls and information theory. Is remembered in this book primarily for his introduction of the Nyquist Stability Criterion.
- Homogeniety
- Property of a system whose scaled input results in an equally scaled output.
- Hybrid Systems
- Systems which have both analog and digital components.
- Impulse
- A function denoted δ(t), that is the derivative of the unit step.
- Impulse Response
- The system output when the system is stimulated by an impulse input. The Inverse Laplace Transform of the transfer function of the system.
- Initial Conditions
- The conditions of the system at time , where t0 is the first time the system is stimulated.
- Initial Value Theorem
- A theorem that allows the initial conditions of the system to be determined from the Transfer function.
- Input-Output Description
- See external description.
- Instantaneous
- A system is instantaneous if the system doesn't have memory, and if the current output of the system is only dependent on the current input. See Dynamic, Memory.
- Integrated Absolute Error (IAE)
- absolute error (ideal vs actual performance) is integrated over the analysis period.
- Integrated Squared Error (ISE)
- squared error (ideal vs actual performance) is integrated over the analysis period.
- Integrators
- A system pole at the origin of the S-plane. Has the effect of integrating the system input.
- Inverse Fourier Transform
- An integral transform that converts a function from the frequency domain into the time-domain.
- Inverse Laplace Transform
- An integral transform that converts a function from the S-domain into the time-domain.
- Inverse Z-Transform
- An integral transform that converts a function from the Z-domain into the discrete time domain.
J, K, L
- Lag
- The observed process impact from an output is slower than the control rate.
- Laplace Transform
- An integral transform that converts a function from the time domain into a complex frequency domain.
- Laplace Transform Domain
- A complex domain where the Laplace Transform of a function is graphed. The imaginary part of s is plotted along the vertical axis, and the real part of s is plotted along the horizontal axis.
- Left Eigenvectors
- Left-hand nullspace solutions to the characteristic equation of a matrix for given eigenvalues. The rows of the inverse transition matrix.
- Linear
- A system that satisfies the superposition principle. See Additive and Homogeneous.
- Linear Time-Invariant
- LTI. See Linear, and Time-Invariant.
- Low Clamp
- User-applied lower bound on control output signal.
- L/R
- Local/Remote operation.
- LQR
- Linear Quadratic Regulator.
- Lumped
- A system with a finite number of states, or a finite number of state variables.
M, N, O
- Magnitude
- the gain component of frequency response. This is often all that is considered in saying a discrete filter's response is well matched to the analog's. It is the DC gain at 0 frequency.
- Marginal Stability
- A system has an oscillatory response, as determined by having imaginary poles or imaginary eigenvalues.
- Mason's Rule
- see [5]
- MATLAB
- Commercial software having a Control Systems toolbox. Also see Octave.
- Memory
- A system has memory if its current output is dependent on previous and current inputs.
- MFAC
- Model Free Adaptive Control.
- MIMO
- A system with multiple inputs and multiple outputs.
- Modern Approach
- see modern controls
- Modern Controls
- A control methodology that uses the state-space representation to analyze and manipulate the Internal Description of a system.
- Modified Z-Transform
- A version of the Z-Transform, expanded to allow for an arbitrary processing delay.
- MPC
- Model Predictive Control.
- MRAC
- Model Reference Adaptive Control.
- MV
- can denote Manipulated variable or Measured variable (not the same)
- Natural Frequency
- The fundamental frequency of the system, the frequency for which the system's frequency response is largest.
- Negative Feedback
- A feedback system where the output signal is subtracted from the input signal, and the difference is input to the plant.
- The Nyquist Criteria
- A necessary and sufficient condition of stability that can be derived from Bode plots.
- Nonlinear Control
- A branch of control engineering that deals exclusively with non-linear systems. We do not cover nonlinear systems in this book.
- OCTAVE
- Open-source software having a Control Systems toolbox. Also see MATLAB.
- Offset
- The discrepancy between desired and actual value after settling. P-only control can give offset.
- Oliver Heaviside
- Electrical Engineer, Introduced the Laplace Transform as a tool for control engineering.
- Open Loop
- when the system is not closed, its behavior has a free-running component rather than controlled
- Optimal Control
- A branch of control engineering that deals with the minimization of system cost, or maximization of system performance.
- Order
- The order of a polynomial is the highest exponent of the independent variable in that exponent. The order of a system is the order of the Transfer Function's denominator polynomial.
- Output equation
- An equation that relates the current system input, and the current system state to the current system output.
- Overshoot
- measures the extent of system response against desired (setpoint tracking).
P, Q, R
- Parabolic
- A parabolic input is defined by the equation.
- Partial Fraction Expansion
- A method by which a complex fraction is decomposed into a sum of simple fractions.
- Percent Overshoot
- PO, the amount by which the step response overshoots the reference value, in percentage of the reference value.
- Phase
- the directional component of frequency response, not typically well-matched between a discrete filter equivalent to the analog version, especially as frequency approaches the Nyquist limit. The final value in the limit drives system stability, and stems from the poles and zeros of the characteristic equation.
- PID
- Proportional-Integral-Derivative
- Plant
- A central system which has been provided, and must be analyzed or controlled.
- PLC
- Programmable Logic Controller
- Pole
- A value for s that causes the denominator of the transfer function to become zero, and therefore causes the transfer function itself to approach infinity.
- Pole-Zero Form
- The transfer function is factored so that the locations of all the poles and zeros are clearly evident.
- Position Error
- The amount of steady-state error of a system stimulated by a unit step input.
- Position Error Constant
- A constant that determines the position error of a system.
- Positive Feedback
- A feedback system where the system output is added to the system input, and the sum is input into the plant.
- PSD
- The power spectral density which shows the distribution of power in the spectrum of a particular signal.
- Pulse Response
- The response of a digital system to a unit step input, in terms of the transfer matrix.
- PV
- Process variable
- Quantized
- A system is quantized if it can only output certain discrete values.
- Quarter-decay
- the time or number of control rates required for process overshoot to be limited to within 1/4 of the maximum peak overshoot (PO) after a SP change. If the PO is 25% at sample time N, this would be time N+k when subsequent PV remains < SP*1.0625, presuming the process is settling.
- Raise-Lower
- Output type that works from present position rather than as a completely new computed spanned output. For R/L, the % change should be applied to the working clamps i.e. 5%(hi clamp-lo clamp).
- Ramp
- A ramp is defined by the function .
- Reconstructors
- A system that converts a digital signal into an analog signal.
- Reference Value
- The target input value of a feedback system.
- Relaxed
- A system is relaxed if the initial conditions are zero.
- Reverse action
- target output decrease is required to bring the process variable (PV) to setpoint (SP) when PV is below SP. Thus, PV decreases with output increase.
- Rise Time
- The amount of time it takes for the step response of the system to reach within a certain range of the reference value. Typically, this range is 80%.
- Robust Control
- A branch of control engineering that deals with systems subject to external and internal noise and disruptions.
S, T, U, V
- Samplers
- A system that converts an analog signal into a digital signal.
- Sampled-Data Systems
- See Hybrid Systems'.
- Sampling Time
- In a discrete system, the sampling time is the amount of time between samples. Reflects the lower bound for Control rate.
- SCADA
- Supervisory Control and Data Acquisition.
- S-Domain
- The domain of the Laplace Transform of a signal or system.
- Second-order System;
- Settling Time
- The amount of time it takes for the system's oscillatory response to be damped to within a certain band of the steady-state value. That band is typically 10%.
- Signal Flow Diagram
- A method of visually representing a system, using arrows to represent the direction of signals in the system.
- SISO
- Single input, single output.
- Span
- the designed operation region of the item,=high range-low range. Working span can be smaller if output clamps are used.
- Stability
- Typically "BIBO Stability", a system with a well-behaved input will result in a well-behaved output. "Well-behaved" in this sense is arbitrary.
- Star Transform
- A version of the Laplace Transform that acts on discrete signals. This transform is implemented as an infinite sum.
- State Equation
- An equation that relates the future states of a system with the current state and the current system input.
- State Transition Matrix:A coefficient matrix, or a matrix function that relates how the system state changes in response to the system input. In time-invariant systems, the state-transition matrix is the matrix exponential of the system matrix.
- State-Space Equations
- A set of equations, typically written in matrix form, that relates the input, the system state, and the output. Consists of the state equation and the output equation. See [6]
- State-Variable
- A vector that describes the internal state of the system.
- Stability
- The system output cannot approach infinity as time approaches infinity. See BIBO, Lyapunov Stability.
- Step Response
- The response of a system when stimulated by a unit-step input. A unit step is a setpoint change for setpoint tracking.
- Steady State
- The output value of the system as time approaches infinity.
- Steady State Error
- At steady state, the amount by which the system output differs from the reference value.
- Superposition
- A system satisfies the condition of superposition if it is both additive and homogeneous.
- System Identification
- method of trying to identify the system characterization , typically through least squares analysis of input,output and noise data vectors. May use ARMA type framework.
- System Type
- The number of ideal integrators in the system.
- Time-Invariant
- A system is time-invariant if an input time-shifted by an arbitrary delay produces an output shifted by that same delay.
- Transfer Function
- The ratio of the system output to its input, in the S-domain. The Laplace Transform of the function's impulse response.
- Transfer Function Matrix:The Laplace transform of the state-space equations of a system, that provides an external description of a MIMO system.
- Uniform Stability
- Also "Uniform BIBO Stability", a system where an input signal in the range [0, 1] results in a finite output from the initial time until infinite time. See [7].
- Unit Step
- An input defined by . Practically, a setpoint change.
- Unity Feedback
- A feedback system where the feedback loop element H has a transfer function of 1.
- Velocity Error
- The amount of steady-state error when the system is stimulated by a ramp input.
- Velocity Error Constant
- A constant that determines that amount of velocity error in a system.
W, X, Y, Z
- W-plane
- Reference plane used in the bilinear transform.
- Wind-up
- when the numerics of computed control adjustment can "wind-up", yielding control correction with an inappropriate component unless prevented. An example is the "I" contribution of PID if output has been disconnected during PID calculation
- Zero
- A value for s that causes the numerator of the transfer function to become zero, and therefore causes the transfer function itself to become zero.
- Zero Input Response
- The response of a system with zero external input. Relies only on the value of the system state to produce output.
- Zero State Response
- The response of the system with zero system state. The output of the system depends only on the system input.
- ZOH
- Zero order hold.
- Z-Transform
- An integral transform that is related to the Laplace transform through a change of variables. The Z-Transform is used primarily with digital systems. See [8]
List of Equations
The following is a list of the important equations from the text, arranged by subject. For more information about these equations, including the meaning of each variable and symbol, the uses of these functions, or the derivations of these equations, see the relevant pages in the main text.
Fundamental Equations
[Euler's Formula]
[Convolution]
[Convolution Theorem]
[Characteristic Equation]
[Decibels]
Basic Inputs
[Unit Step Function]
[Unit Ramp Function]
[Unit Parabolic Function]
Error Constants
[Position Error Constant]
[Velocity Error Constant]
[Acceleration Error Constant]
System Descriptions
[General System Description]
[Convolution Description]
[Transfer Function Description]
[State-Space Equations]
[Transfer Matrix]
[Transfer Matrix Description]
[Mason's Rule]
Feedback Loops
[Closed-Loop Transfer Function]
[Open-Loop Transfer Function]
[Characteristic Equation]
Transforms
[Laplace Transform]
[Inverse Laplace Transform]
[Fourier Transform]
[Inverse Fourier Transform]
[Star Transform]
[Z Transform]
[Inverse Z Transform]
[Modified Z Transform]
Transform Theorems
[Final Value Theorem]
[Initial Value Theorem]
State-Space Methods
[General State Equation Solution]
[General Output Equation Solution]
[Time-Variant General Solution]
[Impulse Response Matrix]
Root Locus
[The Magnitude Equation]
[The Angle Equation]
[Number of Asymptotes]
[Angle of Asymptotes]
[Origin of Asymptotes]
[Breakaway Point Locations]
- or
Lyapunov Stability
[Lyapunov Equation]
Controllers and Compensators
[PID]
Resources and Further Reading
Wikibooks
A number of wikibooks exist on topics that are (a) prerequisites to this book (b) companion pieces to and references for this book, and (c) of further interest to people who have completed reading this book. Below will be a listing of such books, ordered according to the categories listed above.
Prerequisite Books
- Linear algebra
- Linear Algebra with Differential Equations
- Complex Numbers
- Calculus
- Signals and Systems
Companion Books
Books for Further Reading
Wikiversity
The Wikiversity project also contains a number of collaborative learning efforts in the field of control systems, and related subjects. As best as possible, we will attempt to list those efforts here:
Wikiversity is also a place to host learning materials, such as assignments, tests, and reading plans. It is the goal of the authors of this book to create such materials for use in conjunction with this book. As such materials are added to wikiversity, they will be referenced here.
Wikipedia
There are a number of Wikipedia articles on the topics covered in this book, and those articles will be linked to from the appropriate pages of this book. However, some of the articles that are of general use to the book are:
A complete listing of all Wikipedia articles related to this topic can be found at:
Software
Root Locus
Root-Locus is a free program that was used to create several of the images in this book. That software can be obtained from the following web address:
Explicit permission has been granted by the author of the program to include screenshots on wikibooks. Images generated from the Root-Locus program should be included in Category:Root Locus Images, and appropriately tagged as a screenshot of a free software program.
MATLAB
MATLAB, Simulink, the Control Systems Toolbox and the Symbolic Toolbox are trademarks of The MathWorks, Inc. Other product or brand names are trademarks or registered trademarks of their respective holders. For more information about MATLAB, or to purchase a copy, visit:
For information about the proper way to refer to MATLAB, please see:
All MATLAB code appearing in this book has been released under the terms of the GFDL by the respective authors. All screenshots, graphs, and images relating to MATLAB have been produced in Octave, with changes to the original MATLAB code made as necessary.
Octave
Octave is a free open-source alternative program to MATLAB. Octave utilizes a scripting language that is very similar to that of MATLAB, although there are several differences. Most of the basic examples described in this book will work equally well in MATLAB or Octave, with no changes or only minor changes. For more information, or to download a copy of Octave, visit:
Commercial Vendors
The following are some common vendors of control-related hardware and software. These links are for personal interest only, and do not constitute an official endorsement of the companies by Wikibooks.
External Publications
The following books and resources were used as reference works in the creation of this wikibook (books listed in alphabetical order).
- Brogan, William L, Modern Control Theory, 3rd Edition, 1991. ISBN 0135897637
- Chen, Chi-Tsong, Linear System Theory and Design, 3rd Edition, 1999. ISBN 0195117778
- Dorf and Bishop, Modern Control Systems, 10th Edition, Prentice Hall, 2005. ISBN 0131277650
- Hamming, Richard, Numerical Methods for Scientists and Engineers, 2nd edition, Dover, 1987. ISBN 0486652416
- Kalman, R. E., When is a linear control system optimal, ASME Transactions, Journal of Basic Engineering, 1964
- Kalman, R. E., On the General Theory of Control Systems, IRE Transactions on Automatic Control, Volume 4, Issue 3, p110, 1959. ISSN 0096199X
- Ogata, Katsuhiko, Solving Control Engineering Problems with MATLAB, Prentice Hall, New Jersey, 1994. ISBN 0130459070
- Phillips and Nagle, Digital Control System Analysis and Design, 3rd Edition, Prentice Hall, 1995. ISBN 013309832X
The following books and resources are suitable for further reading.
- DiStefano, Stubberud, Williams, Schaum's Outline Series Feedback and Control Systems, 2nd Edition, 1997. ISBN 0070170479
- Franklin, Powell, Workman, Digital Control of Dynamic Systems, 3rd Edition, 1997. ISBN 9780201820546
- Brosilow, Joseph, Techniques of Model-Based Control, 2002. ISBN 013028078X
External Resources
- IEEE Control Systems Society
- ControlTheoryPro.com A place for controls theory, application, and modeling help.
- University of Michigan Chemical Engineering Process Dynamics and Controls Open Textbook
Licensing
License
The text of this wikibook is released under the terms of the GNU Free Documentation License version 1.2. The particular version of that license that is being used can be found at:
The text of that license will also be appended to the end of the printable version of this wikibook.
Images used in this document may not be released under the GFDL, and the licenses used with each image in this book will be listed in a table below. Some contributors may cross-license their contributions under the GFDL and another compatible license. Some contributions have been released into the public domain.
Images
The individual images used in this wikibook are released under a variety of different licenses, including the GFDL, and Creative-Commons licenses. Some images have been released into the public domain. The following table will list the images used in this book, along with the license under which the image is released, and any additional information about the images that is needed under the terms of the applicable licenses.
Authors
The authors of this text can list themselves below. Authors should be listed in alphabetical order by first name (if a real name is used), or by username. This is not a canonical list.
The usernames of additional contributors, as well as the size and scope of the contributions made by the authors listed above can be found in the history records of the individual pages on the Wikibooks website. Those history pages satisfy the attribution requirement of the GFDL, and any lists of authors that appear here or anywhere else do not count as legal attribution under the terms of that license.
Child Versions
The Control Systems wikibook is offered with a number of child versions, which represent subsets of the material available in the parent book. Because certain chapters are omitted from the child versions, some of the images listed above may not be present, and some of the authors listed above may not have made any contributions to some printed and distributed versions of this text.
License: GFDL
As of July 15, 2009 Wikibooks has moved to a dual-licensing system that supersedes the previous GFDL only licensing. In short, this means that text licensed under the GFDL only can no longer be imported to Wikibooks, retroactive to 1 November 2008. Additionally, Wikibooks text might or might not now be exportable under the GFDL depending on whether or not any content was added and not removed since July 15. |
Version 1.3, 3 November 2008 Copyright (C) 2000, 2001, 2002, 2007, 2008 Free Software Foundation, Inc. <http://fsf.org/>
Everyone is permitted to copy and distribute verbatim copies of this license document, but changing it is not allowed.
0. PREAMBLE
The purpose of this License is to make a manual, textbook, or other functional and useful document "free" in the sense of freedom: to assure everyone the effective freedom to copy and redistribute it, with or without modifying it, either commercially or noncommercially. Secondarily, this License preserves for the author and publisher a way to get credit for their work, while not being considered responsible for modifications made by others.
This License is a kind of "copyleft", which means that derivative works of the document must themselves be free in the same sense. It complements the GNU General Public License, which is a copyleft license designed for free software.
We have designed this License in order to use it for manuals for free software, because free software needs free documentation: a free program should come with manuals providing the same freedoms that the software does. But this License is not limited to software manuals; it can be used for any textual work, regardless of subject matter or whether it is published as a printed book. We recommend this License principally for works whose purpose is instruction or reference.
1. APPLICABILITY AND DEFINITIONS
This License applies to any manual or other work, in any medium, that contains a notice placed by the copyright holder saying it can be distributed under the terms of this License. Such a notice grants a world-wide, royalty-free license, unlimited in duration, to use that work under the conditions stated herein. The "Document", below, refers to any such manual or work. Any member of the public is a licensee, and is addressed as "you". You accept the license if you copy, modify or distribute the work in a way requiring permission under copyright law.
A "Modified Version" of the Document means any work containing the Document or a portion of it, either copied verbatim, or with modifications and/or translated into another language.
A "Secondary Section" is a named appendix or a front-matter section of the Document that deals exclusively with the relationship of the publishers or authors of the Document to the Document's overall subject (or to related matters) and contains nothing that could fall directly within that overall subject. (Thus, if the Document is in part a textbook of mathematics, a Secondary Section may not explain any mathematics.) The relationship could be a matter of historical connection with the subject or with related matters, or of legal, commercial, philosophical, ethical or political position regarding them.
The "Invariant Sections" are certain Secondary Sections whose titles are designated, as being those of Invariant Sections, in the notice that says that the Document is released under this License. If a section does not fit the above definition of Secondary then it is not allowed to be designated as Invariant. The Document may contain zero Invariant Sections. If the Document does not identify any Invariant Sections then there are none.
The "Cover Texts" are certain short passages of text that are listed, as Front-Cover Texts or Back-Cover Texts, in the notice that says that the Document is released under this License. A Front-Cover Text may be at most 5 words, and a Back-Cover Text may be at most 25 words.
A "Transparent" copy of the Document means a machine-readable copy, represented in a format whose specification is available to the general public, that is suitable for revising the document straightforwardly with generic text editors or (for images composed of pixels) generic paint programs or (for drawings) some widely available drawing editor, and that is suitable for input to text formatters or for automatic translation to a variety of formats suitable for input to text formatters. A copy made in an otherwise Transparent file format whose markup, or absence of markup, has been arranged to thwart or discourage subsequent modification by readers is not Transparent. An image format is not Transparent if used for any substantial amount of text. A copy that is not "Transparent" is called "Opaque".
Examples of suitable formats for Transparent copies include plain ASCII without markup, Texinfo input format, LaTeX input format, SGML or XML using a publicly available DTD, and standard-conforming simple HTML, PostScript or PDF designed for human modification. Examples of transparent image formats include PNG, XCF and JPG. Opaque formats include proprietary formats that can be read and edited only by proprietary word processors, SGML or XML for which the DTD and/or processing tools are not generally available, and the machine-generated HTML, PostScript or PDF produced by some word processors for output purposes only.
The "Title Page" means, for a printed book, the title page itself, plus such following pages as are needed to hold, legibly, the material this License requires to appear in the title page. For works in formats which do not have any title page as such, "Title Page" means the text near the most prominent appearance of the work's title, preceding the beginning of the body of the text.
The "publisher" means any person or entity that distributes copies of the Document to the public.
A section "Entitled XYZ" means a named subunit of the Document whose title either is precisely XYZ or contains XYZ in parentheses following text that translates XYZ in another language. (Here XYZ stands for a specific section name mentioned below, such as "Acknowledgements", "Dedications", "Endorsements", or "History".) To "Preserve the Title" of such a section when you modify the Document means that it remains a section "Entitled XYZ" according to this definition.
The Document may include Warranty Disclaimers next to the notice which states that this License applies to the Document. These Warranty Disclaimers are considered to be included by reference in this License, but only as regards disclaiming warranties: any other implication that these Warranty Disclaimers may have is void and has no effect on the meaning of this License.
2. VERBATIM COPYING
You may copy and distribute the Document in any medium, either commercially or noncommercially, provided that this License, the copyright notices, and the license notice saying this License applies to the Document are reproduced in all copies, and that you add no other conditions whatsoever to those of this License. You may not use technical measures to obstruct or control the reading or further copying of the copies you make or distribute. However, you may accept compensation in exchange for copies. If you distribute a large enough number of copies you must also follow the conditions in section 3.
You may also lend copies, under the same conditions stated above, and you may publicly display copies.
3. COPYING IN QUANTITY
If you publish printed copies (or copies in media that commonly have printed covers) of the Document, numbering more than 100, and the Document's license notice requires Cover Texts, you must enclose the copies in covers that carry, clearly and legibly, all these Cover Texts: Front-Cover Texts on the front cover, and Back-Cover Texts on the back cover. Both covers must also clearly and legibly identify you as the publisher of these copies. The front cover must present the full title with all words of the title equally prominent and visible. You may add other material on the covers in addition. Copying with changes limited to the covers, as long as they preserve the title of the Document and satisfy these conditions, can be treated as verbatim copying in other respects.
If the required texts for either cover are too voluminous to fit legibly, you should put the first ones listed (as many as fit reasonably) on the actual cover, and continue the rest onto adjacent pages.
If you publish or distribute Opaque copies of the Document numbering more than 100, you must either include a machine-readable Transparent copy along with each Opaque copy, or state in or with each Opaque copy a computer-network location from which the general network-using public has access to download using public-standard network protocols a complete Transparent copy of the Document, free of added material. If you use the latter option, you must take reasonably prudent steps, when you begin distribution of Opaque copies in quantity, to ensure that this Transparent copy will remain thus accessible at the stated location until at least one year after the last time you distribute an Opaque copy (directly or through your agents or retailers) of that edition to the public.
It is requested, but not required, that you contact the authors of the Document well before redistributing any large number of copies, to give them a chance to provide you with an updated version of the Document.
4. MODIFICATIONS
You may copy and distribute a Modified Version of the Document under the conditions of sections 2 and 3 above, provided that you release the Modified Version under precisely this License, with the Modified Version filling the role of the Document, thus licensing distribution and modification of the Modified Version to whoever possesses a copy of it. In addition, you must do these things in the Modified Version:
- Use in the Title Page (and on the covers, if any) a title distinct from that of the Document, and from those of previous versions (which should, if there were any, be listed in the History section of the Document). You may use the same title as a previous version if the original publisher of that version gives permission.
- List on the Title Page, as authors, one or more persons or entities responsible for authorship of the modifications in the Modified Version, together with at least five of the principal authors of the Document (all of its principal authors, if it has fewer than five), unless they release you from this requirement.
- State on the Title page the name of the publisher of the Modified Version, as the publisher.
- Preserve all the copyright notices of the Document.
- Add an appropriate copyright notice for your modifications adjacent to the other copyright notices.
- Include, immediately after the copyright notices, a license notice giving the public permission to use the Modified Version under the terms of this License, in the form shown in the Addendum below.
- Preserve in that license notice the full lists of Invariant Sections and required Cover Texts given in the Document's license notice.
- Include an unaltered copy of this License.
- Preserve the section Entitled "History", Preserve its Title, and add to it an item stating at least the title, year, new authors, and publisher of the Modified Version as given on the Title Page. If there is no section Entitled "History" in the Document, create one stating the title, year, authors, and publisher of the Document as given on its Title Page, then add an item describing the Modified Version as stated in the previous sentence.
- Preserve the network location, if any, given in the Document for public access to a Transparent copy of the Document, and likewise the network locations given in the Document for previous versions it was based on. These may be placed in the "History" section. You may omit a network location for a work that was published at least four years before the Document itself, or if the original publisher of the version it refers to gives permission.
- For any section Entitled "Acknowledgements" or "Dedications", Preserve the Title of the section, and preserve in the section all the substance and tone of each of the contributor acknowledgements and/or dedications given therein.
- Preserve all the Invariant Sections of the Document, unaltered in their text and in their titles. Section numbers or the equivalent are not considered part of the section titles.
- Delete any section Entitled "Endorsements". Such a section may not be included in the Modified version.
- Do not retitle any existing section to be Entitled "Endorsements" or to conflict in title with any Invariant Section.
- Preserve any Warranty Disclaimers.
If the Modified Version includes new front-matter sections or appendices that qualify as Secondary Sections and contain no material copied from the Document, you may at your option designate some or all of these sections as invariant. To do this, add their titles to the list of Invariant Sections in the Modified Version's license notice. These titles must be distinct from any other section titles.
You may add a section Entitled "Endorsements", provided it contains nothing but endorsements of your Modified Version by various parties—for example, statements of peer review or that the text has been approved by an organization as the authoritative definition of a standard.
You may add a passage of up to five words as a Front-Cover Text, and a passage of up to 25 words as a Back-Cover Text, to the end of the list of Cover Texts in the Modified Version. Only one passage of Front-Cover Text and one of Back-Cover Text may be added by (or through arrangements made by) any one entity. If the Document already includes a cover text for the same cover, previously added by you or by arrangement made by the same entity you are acting on behalf of, you may not add another; but you may replace the old one, on explicit permission from the previous publisher that added the old one.
The author(s) and publisher(s) of the Document do not by this License give permission to use their names for publicity for or to assert or imply endorsement of any Modified Version.
5. COMBINING DOCUMENTS
You may combine the Document with other documents released under this License, under the terms defined in section 4 above for modified versions, provided that you include in the combination all of the Invariant Sections of all of the original documents, unmodified, and list them all as Invariant Sections of your combined work in its license notice, and that you preserve all their Warranty Disclaimers.
The combined work need only contain one copy of this License, and multiple identical Invariant Sections may be replaced with a single copy. If there are multiple Invariant Sections with the same name but different contents, make the title of each such section unique by adding at the end of it, in parentheses, the name of the original author or publisher of that section if known, or else a unique number. Make the same adjustment to the section titles in the list of Invariant Sections in the license notice of the combined work.
In the combination, you must combine any sections Entitled "History" in the various original documents, forming one section Entitled "History"; likewise combine any sections Entitled "Acknowledgements", and any sections Entitled "Dedications". You must delete all sections Entitled "Endorsements".
6. COLLECTIONS OF DOCUMENTS
You may make a collection consisting of the Document and other documents released under this License, and replace the individual copies of this License in the various documents with a single copy that is included in the collection, provided that you follow the rules of this License for verbatim copying of each of the documents in all other respects.
You may extract a single document from such a collection, and distribute it individually under this License, provided you insert a copy of this License into the extracted document, and follow this License in all other respects regarding verbatim copying of that document.
7. AGGREGATION WITH INDEPENDENT WORKS
A compilation of the Document or its derivatives with other separate and independent documents or works, in or on a volume of a storage or distribution medium, is called an "aggregate" if the copyright resulting from the compilation is not used to limit the legal rights of the compilation's users beyond what the individual works permit. When the Document is included in an aggregate, this License does not apply to the other works in the aggregate which are not themselves derivative works of the Document.
If the Cover Text requirement of section 3 is applicable to these copies of the Document, then if the Document is less than one half of the entire aggregate, the Document's Cover Texts may be placed on covers that bracket the Document within the aggregate, or the electronic equivalent of covers if the Document is in electronic form. Otherwise they must appear on printed covers that bracket the whole aggregate.
8. TRANSLATION
Translation is considered a kind of modification, so you may distribute translations of the Document under the terms of section 4. Replacing Invariant Sections with translations requires special permission from their copyright holders, but you may include translations of some or all Invariant Sections in addition to the original versions of these Invariant Sections. You may include a translation of this License, and all the license notices in the Document, and any Warranty Disclaimers, provided that you also include the original English version of this License and the original versions of those notices and disclaimers. In case of a disagreement between the translation and the original version of this License or a notice or disclaimer, the original version will prevail.
If a section in the Document is Entitled "Acknowledgements", "Dedications", or "History", the requirement (section 4) to Preserve its Title (section 1) will typically require changing the actual title.
9. TERMINATION
You may not copy, modify, sublicense, or distribute the Document except as expressly provided under this License. Any attempt otherwise to copy, modify, sublicense, or distribute it is void, and will automatically terminate your rights under this License.
However, if you cease all violation of this License, then your license from a particular copyright holder is reinstated (a) provisionally, unless and until the copyright holder explicitly and finally terminates your license, and (b) permanently, if the copyright holder fails to notify you of the violation by some reasonable means prior to 60 days after the cessation.
Moreover, your license from a particular copyright holder is reinstated permanently if the copyright holder notifies you of the violation by some reasonable means, this is the first time you have received notice of violation of this License (for any work) from that copyright holder, and you cure the violation prior to 30 days after your receipt of the notice.
Termination of your rights under this section does not terminate the licenses of parties who have received copies or rights from you under this License. If your rights have been terminated and not permanently reinstated, receipt of a copy of some or all of the same material does not give you any rights to use it.
10. FUTURE REVISIONS OF THIS LICENSE
The Free Software Foundation may publish new, revised versions of the GNU Free Documentation License from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to address new problems or concerns. See http://www.gnu.org/copyleft/.
Each version of the License is given a distinguishing version number. If the Document specifies that a particular numbered version of this License "or any later version" applies to it, you have the option of following the terms and conditions either of that specified version or of any later version that has been published (not as a draft) by the Free Software Foundation. If the Document does not specify a version number of this License, you may choose any version ever published (not as a draft) by the Free Software Foundation. If the Document specifies that a proxy can decide which future versions of this License can be used, that proxy's public statement of acceptance of a version permanently authorizes you to choose that version for the Document.
11. RELICENSING
"Massive Multiauthor Collaboration Site" (or "MMC Site") means any World Wide Web server that publishes copyrightable works and also provides prominent facilities for anybody to edit those works. A public wiki that anybody can edit is an example of such a server. A "Massive Multiauthor Collaboration" (or "MMC") contained in the site means any set of copyrightable works thus published on the MMC site.
"CC-BY-SA" means the Creative Commons Attribution-Share Alike 3.0 license published by Creative Commons Corporation, a not-for-profit corporation with a principal place of business in San Francisco, California, as well as future copyleft versions of that license published by that same organization.
"Incorporate" means to publish or republish a Document, in whole or in part, as part of another Document.
An MMC is "eligible for relicensing" if it is licensed under this License, and if all works that were first published under this License somewhere other than this MMC, and subsequently incorporated in whole or in part into the MMC, (1) had no cover texts or invariant sections, and (2) were thus incorporated prior to November 1, 2008.
The operator of an MMC Site may republish an MMC contained in the site under CC-BY-SA on the same site at any time before August 1, 2009, provided the MMC is eligible for relicensing.
How to use this License for your documents
To use this License in a document you have written, include a copy of the License in the document and put the following copyright and license notices just after the title page:
- Copyright (c) YEAR YOUR NAME.
- Permission is granted to copy, distribute and/or modify this document
- under the terms of the GNU Free Documentation License, Version 1.3
- or any later version published by the Free Software Foundation;
- with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts.
- A copy of the license is included in the section entitled "GNU
- Free Documentation License".
If you have Invariant Sections, Front-Cover Texts and Back-Cover Texts, replace the "with...Texts." line with this:
- with the Invariant Sections being LIST THEIR TITLES, with the
- Front-Cover Texts being LIST, and with the Back-Cover Texts being LIST.
If you have Invariant Sections without Cover Texts, or some other combination of the three, merge those two alternatives to suit the situation.
If your document contains nontrivial examples of program code, we recommend releasing these examples in parallel under your choice of free software license, such as the GNU General Public License, to permit their use in free software.






















![{\displaystyle y_{1}(t)+y_{2}(t)=\sin(3[x_{1}(t)+x_{2}(t)])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ba2f7c9836de496ce51a81ecca7b1c9d80797db)













![{\displaystyle {\frac {d[Ay_{1}(t)+By_{2}(t)]}{dt}}+[Ay_{1}(t)+By_{2}(t)]=Ax_{1}(t)+Bx_{2}(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/795648dd73c7543f766980b6d13575ef440fc540)
![{\displaystyle {\frac {d}{dt}}[Ay_{1}(t)+By_{2}(t)]+[Ay_{1}(t)+By_{2}(t)]=Ax_{1}(t)+Bx_{2}(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c9ccff69dfa467e5f9ec7317275c78bf13068d0)





















![{\displaystyle x[n]=x(nT)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf9d6e2763c5e892b633aaf8be4bf00618515188)







































![{\displaystyle x'(t)=g[t_{0},t,x(t),x(0),u(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2903d46173b2a348e03b65d1f96aba73a4ceba86)
![{\displaystyle y(t)=h[t,x(t),u(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/811fb82c3d63c47d1476f46b6216b95e789ca2f5)


![{\displaystyle \mathbf {x} '(t)=\mathbf {g} [t_{0},t,\mathbf {x} (t),x(0),\mathbf {u} (t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54b5bf74126609e338756aebf53efa379969bf4b)
![{\displaystyle \mathbf {y} (t)=\mathbf {h} [t,\mathbf {x} (t),\mathbf {u} (t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb2b09529eaa5a4def12797084706ed7be1c6faa)
![{\displaystyle \mathbf {x} '(t)=\mathbf {g} [\mathbf {x} (t),x(0),\mathbf {u} (t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11ba8cfc93eaf6d8b859d00a640ff6011f2447a8)
![{\displaystyle \mathbf {y} (t)=\mathbf {h} [\mathbf {x} (t),\mathbf {u} (t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b10e29de2224b70e11a7dd0debf5da9fe1ee51c1)
![{\displaystyle A=\mathbf {g} _{x}[x(0),x(0),u(0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea769938a0de47d019b0d951305e6c940d5452a6)
![{\displaystyle B=\mathbf {g} _{u}[x(0),x(0),u(0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c09df64c13e3d0fe484fbdc75cc177851fa3ab10)
![{\displaystyle C=\mathbf {h} _{x}[x(0),u(0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a048d5afec4ce436b88f8a992df7bf87771443c1)
![{\displaystyle D=\mathbf {h} _{u}[x(0),u(0)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffb7c46a58d4ea9f4c7c3277b6241a0b30710073)


























![{\displaystyle {\frac {d}{dt}}\left[{\frac {d^{2}y(t)}{dt^{2}}}+a_{2}{\frac {dy(t)}{dt}}+a_{1}y(t)\right]+a_{0}y(t)=u(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91ae50bbf54ebdcf676cc41c051a958b617a5fe6)



![{\displaystyle {\frac {d}{dt}}\left[\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07cc12f48d43a20626e118fbf9174d8ebb697e61)













![{\displaystyle x[k+1]=(1+AT)x[k]+TBu[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/647be818acee89ee86f4fff4b1dcae21b87c1308)
![{\displaystyle x[n+1]=A_{d}x[n]+B_{d}u[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad56846e6c571437930a32f9c7e1ebcf46aa070e)
![{\displaystyle y[n]=C_{d}x[n]+D_{d}u[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6de1e72c3b68649965cbb34997f67677182b252)






















![{\displaystyle e^{At}={\mathcal {L}}^{-1}[(sI-A)^{-1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8477ae473bc21f6b84d50512701673c0d77685d7)

































![{\displaystyle A(t)\left[\int _{\tau }^{t}A(\zeta )d\zeta \right]=\left[\int _{\tau }^{t}A(\zeta )d\zeta \right]A(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6f560446274ac432b8ea542c7a3b64ef2aa29de)

























































![{\displaystyle {\mathcal {L}}[X'(t)]={\mathcal {L}}[AX(t)]+{\mathcal {L}}[BU(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3525f69cc3db07a656f201e5eaf923c746c6a96f)
![{\displaystyle {\mathcal {L}}[Y(t)]={\mathcal {L}}[CX(t)]+{\mathcal {L}}[DU(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfeddd43449bab343eabda7b2de536cb91c09731)



![{\displaystyle \mathbf {[} sI-A]{X}(s)=X(0)+B\mathbf {U} (s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89ffd29c50033a0bc0dd4ae1c2d1a0b0489a7c3a)
![{\displaystyle \mathbf {X} (s)=[sI-A]^{-1}X(0)+[sI-A]^{-1}B\mathbf {U} (s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fbcb6b84a1420c0bbc6f659e196ee416743646c)
![{\displaystyle \mathbf {Y} (s)=C([sI-A]^{-1}X(0)+[sI-A]^{-1}B\mathbf {U} (s))+D\mathbf {U} (s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c2221334b54819fb556827eaaab39db0fea4ddb)
![{\displaystyle \mathbf {Y} (s)=C[sI-A]^{-1}X(0)+C[sI-A]^{-1}B\mathbf {U} (s)+D\mathbf {U} (s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dccee4d6e8458ffd5932bacc74069ead33f8ca7)
![{\displaystyle \mathbf {Y} (s)=(C[sI-A]^{-1}B+D)\mathbf {U} (s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aaffe7c0d9bafb3f05e3c84996a414a94c5ae85a)
![{\displaystyle C[sI-A]^{-1}B+D=\mathbf {H} (s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d37ee2188135370b2d768fcf965161d688cd12f6)


![{\displaystyle \mathbf {Y} (s)=C[sI-A]^{-1}\mathbf {x} (0)+(C[sI-A]^{-1}B+D)\mathbf {U} (s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e2ea06c7550ad0c6d2b3124aa657d46a030b4b4)
![{\displaystyle C[sI-A]^{-1}X(0)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fceb02f48681be50ac4450a7364532ad119fd28e)
![{\displaystyle (C[sI-A]^{-1}B+D)\mathbf {U} (s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d6135ceee869daaef3a0dc4d7bfc9a76702cb3c)
![{\displaystyle \mathbf {X} (z)=[zI-A]^{-1}zX(0)+[zI-A]^{-1}B\mathbf {U} (z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be66131d70b42fec8e9125a9b57820b0a00ddea8)
![{\displaystyle \mathbf {Y} (z)=C[zI-A]^{-1}zX(0)+C[zI-A]^{-1}B\mathbf {U} (z)+D\mathbf {U} (z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46907e452482d65a545e35a11d09fabfc51e658a)
![{\displaystyle \mathbf {Y} (z)=(C[zI-A]^{-1}B+D)\mathbf {U} (z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4234641b75e64db84abcdd2527f335ea2ac1e7a)
![{\displaystyle C[zI-A]^{-1}B+D=\mathbf {H} (z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/151e79dc41cb1fb26cf6964a0f9621bd4b69c7a1)

![{\displaystyle x[k+1]=Ax[k]+Bu[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/968e943803299b5d109c4f8c3c9f30267d4253a6)
![{\displaystyle y[k]=Cx[k]+Du[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f519a3e55979d6f94be1a47fcec83f3b7c6d06f)

























![{\displaystyle y(t)=[x(t)*f(t)]*g(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a0488880d8f05d9b027049a990068156208f23c)
![{\displaystyle y(t)=x(t)*[f(t)*g(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03509cd1b7232b1efcd50d7465edcd099fc55ca4)
![{\displaystyle Y(s)=X(s)[F(s)G(s)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6b1a109584722e3f49b210628de10b53a0dcf4c)






![{\displaystyle Y(s)=X(s)[F(s)+G(s)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c9423d78177f705eaad381153cb374ed520cb7c)
![{\displaystyle y(t)=x(t)*[f(t)+g(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76847ae33b40004c521daa714dd6fbccb4b5c3cb)








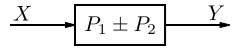








































































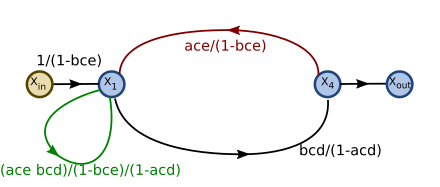























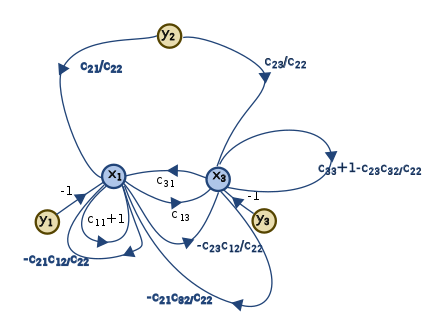


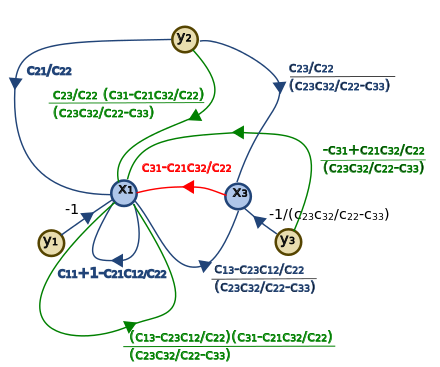












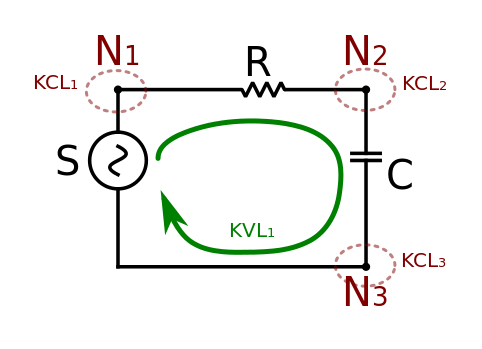










































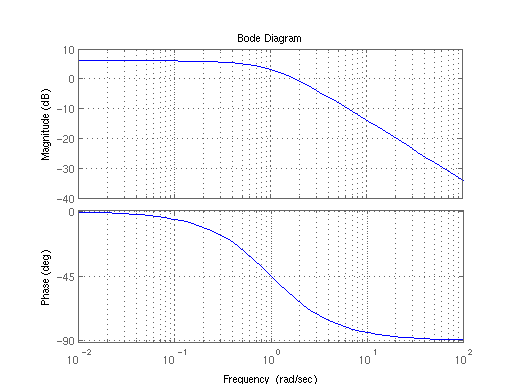





















![{\displaystyle x[n_{0}]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b6475aebd307d5c470fd8e34059615fcb0cd4861)
![{\displaystyle \|u[n]\|\leq k}](https://wikimedia.org/api/rest_v1/media/math/render/svg/303eccf67e1d761aa092eee351727bc3108d9e09)

![{\displaystyle \|y[n]\|\leq L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b8bf7f608ba8292dd99c8721ea388a903cfa32e)
![{\displaystyle G[n]=\left\{{\begin{matrix}CA^{k-1}B&{\mbox{ if }}k>0\\0&{\mbox{ if }}k\leq 0\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a3c7e26c324cb2aad5a5940457bfba00e3f77ce)
![{\displaystyle G[n]=\left\{{\begin{matrix}C\phi [n,n_{0}]B&{\mbox{ if }}k>0\\0&{\mbox{ if }}k\leq 0\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57c455ebe07eb605f959ad30aa1c65f4093b0783)
![{\displaystyle \sum _{n=0}^{k}\|G[n]\|\leq L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c006c870844644293fd834f0c0e1250b8fb800d)







![{\displaystyle \operatorname {sup} _{t\geq 0}[\operatorname {sup} _{t\geq t_{0}}\|\phi (t,t_{0})\|]=k_{0}<\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b693a4c15c1084ec796619154d0d88321e8a2154)






















![{\displaystyle \operatorname {rank} [\lambda I-A,B]=p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b340340b41e8c39dfe637e3766968cb57648af0)

























![{\displaystyle D(z)=K_{p}+K_{i}{\frac {T}{2}}\left[{\frac {z+1}{z-1}}\right]+K_{d}\left[{\frac {z-1}{Tz}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aafdc2121c235d8b68ee53d6103c157ef86057ac)






![{\displaystyle y[n]=x[n]a_{0}+x[n-1]a_{1}+x[n-2]a_{2}-y[n-1]b_{1}-y[n-2]b_{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2343121cdc7e1bb59f60ce94911e2a0383fec093)



















![{\displaystyle x'[t]=Ax[t]+Bu[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96c9bb4a5c7de3cd5cc4e8cd7e1918b929fb2d4b)
![{\displaystyle y[t]=Cx[t]+Du[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a693829a3890a121c299963d4a80d4af64ac1c12)
![{\displaystyle x'[t]=A[t]x[t]+B[t]u[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4650e82120f9b61badbfa572264a77149807ee4a)
![{\displaystyle y[t]=C[t]x[t]+D[t]u[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a3b4e2adcb61cdc6d41a7a7d964d06bd1e2920f)











![{\displaystyle [A|I]\to [I|B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/013631483d1dbc297e1efab7bfe844fec0b54e20)



![{\displaystyle T=[v_{1}v_{2}\cdots v_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb382a2a0e3e0210260963378e41a6e924b05748)










![{\displaystyle =1-abs(PV-SP)/max[PVmax-SP,SP-PVmin]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a34d47acce2287268821b38f7a46ad1f4debaf7)






![{\displaystyle {\mathcal {L}}[f(t)*g(t)]=F(s)G(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1da7a021eb1cc9ce933aee9c48544308fd9aea4b)
![{\displaystyle {\mathcal {L}}[f(t)g(t)]=F(s)*G(s)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4a5783272e7260e8336adb5853f8a66ffc23d02)




![{\displaystyle F(s)={\mathcal {L}}[f(t)]=\int _{0}^{\infty }f(t)e^{-st}dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c38c98774feaf400f8af0dab5f8aed8aed5d06f)

![{\displaystyle F(j\omega )={\mathcal {F}}[f(t)]=\int _{0}^{\infty }f(t)e^{-j\omega t}dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccad40df03382f6ead04ba196a52314f1b7a4291)

![{\displaystyle F^{*}(s)={\mathcal {L}}^{*}[f(t)]=\sum _{i=0}^{\infty }f(iT)e^{-siT}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30b1617367f1700032ffd3f5b8720159699648ed)
![{\displaystyle X(z)={\mathcal {Z}}\left\{x[n]\right\}=\sum _{i=-\infty }^{\infty }x[n]z^{-n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af2109d64c2b69a9a5104d600e08fc9b4267360b)
![{\displaystyle x[n]=Z^{-1}\{X(z)\}={\frac {1}{2\pi j}}\oint _{C}X(z)z^{n-1}dz\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2de87f7a38f4c6528c53a5883b209edf50d3a62)
![{\displaystyle X(z,m)={\mathcal {Z}}(x[n],m)=\sum _{n=-\infty }^{\infty }x[n+m-1]z^{-n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85540c08a77b2c40043f7f7e84c0ed56437bb4a9)

![{\displaystyle x[\infty ]=\lim _{z\to 1}(z-1)X(z)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30f34e1769d16e186e49651f66f4401a8c589b3e)


![{\displaystyle x[n]=A^{n}x[0]+\sum _{m=0}^{n-1}A^{n-1-m}Bu[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37dfa3802c72fcf32ac7e379d52ae691154fad04)

![{\displaystyle y[n]=CA^{n}x[0]+\sum _{m=0}^{n-1}CA^{n-1-m}Bu[n]+Du[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08c5007961a18ea382ac3c879331fb4e87873560)

![{\displaystyle x[n]=\phi [n,n_{0}]x[t_{0}]+\sum _{m=n_{0}}^{n}\phi [n,m+1]B[m]u[m]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44156ca6ba03d51f16817e0cd51292ca38563a80)

![{\displaystyle G[n]=\left\{{\begin{matrix}CA^{k-1}N&{\mbox{ if }}k>0\\0&{\mbox{ if }}k\leq 0\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/90177e0e9300b0985968117dde9fa1f3a5aec597)








