Communication Systems/Microwave Systems
Microwaves are high frequency radio waves (> 1 GHz) and they propagate much like any other electromagnetic phenomenon in free space. Because they are electromagnetic waves and not electrons, they do not propagate well down copper cables. instead, the waves are guided down hollow conductors.
Waveguides[edit | edit source]
Two boundary conditions must be met in a waveguide for a wave to travel down the guide:
- • The electric field must terminate normally on the conductor (the tangential component of the electric field must be zero).
- • The magnetic field must lie entirely tangent along the wall surface. (the normal component of the magnetic field must be zero).
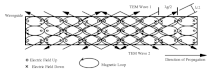
Consequently, TEM waves cannot be conducted in a waveguide. (Recall that in a TEM wave, the electric and magnetic fields are at right angles to each other and the direction of propagation.)
The most common wave used in waveguides is the TE10, meaning transverse electric. The subscript TEab denotes the number of half cycles which appear in the a and b dimensions of the waveguide.
There are many other waveguide modes. A TE10 wave may be formed when two TEM wave intersect:
- The velocity of a TEM wave in air is:
- The phase velocity (the apparent wave velocity along the guide wall) of a TE wave:
- Therefor the phase or guide velocity is:
- From the right angle triangle BCD, we obtain:
- From the right angle triangle ABD we obtain:
Since
- We obtain:
- We obtain:
- or
- or
- where
- guide wavelength for the TE10 mode
- free space wavelength of the TEM wave
- broad dimension of the waveguide
- where
When , the guide wavelength becomes infinite. This corresponds to a TEM wave bouncing from side to side in the guide with no velocity component along the guide. This is cutoff wavelength and represents the lowest frequency that can be propagated.
Phase & Group Velocity
The equations above can be manipulated to obtain:
This means that the phase velocity is always greater than the speed of light. The TEM components zigzag through the guide at the speed of light, but they convey power at the group velocity. The group velocity is always less than the speed of light.
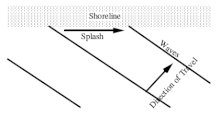
Analogy
Nothing physical can exceed the speed of light, but it is possible for some aspect of a wave to exceed light speed. For example, the splash that occurs when a wave washes up on the beach can travel faster than the wave, if it strikes at some angle other than 900.
- Example
- A rectangular waveguide measuring 0.9 by 0.45 inches is fed with a 10 GHz carrier. Determine if a TE10 wave will propagate, and if so, determine its guide wavelength, group velocity and phase velocity.
- Since , a TE10 wave will propagate.
Wave Impedance[edit | edit source]
The ratio of the transverse electric and magnetic fields constitutes an impedance. This should not be considered the same as a resistance, because it does not dissipate power.
The TE10 wave consists of two equal TEM waves where the electric field is transverse along the b dimension but the magnetic field is along the a dimension is described by: . Consequently, the wave impedance is:
- For a TEM wave:
Therefore:
- or
- for TE waves.
- for TM waves.
A TE wave has a characteristic impedance . As the cutoff frequency is approached, the impedance approaches infinity. These modes are generated by means of a vertical probe antenna.
A TM wave has a characteristic impedance . As the cutoff frequency is approached, the impedance approaches zero. These modes are generated by means of a horizontal probe antenna.
A waveguide with a dielectric other than air will have its cutoff wavelength increased by the square root of the dielectric constant.
Waveguide attenuation characteristics are quite complex and are generally derived empirically. Attenuation varies with interior wall coating, guide dimensions, and operating frequency Attenuation can occur because the induced wall currents are electrons interacting with the guide.
There is a limit to the amount of power which can be conveyed in a guide. If this limit is exceeded, electrical arcing will occur and severe attenuation results. The maximum power handling capability of an air filled rectangular waveguide operating in the TE mode is:
- where Emax = maximum voltage gradient in v/cm
Standing Waves[edit | edit source]
Standing waves act much like the plucked string on a guitar. The signal magnitude changes but its location does not. One of the most useful places to create a standing wave is at a radiating antenna, but it may also be useful to create one in a guide.
Wall Currents
Traveling waves are time invariant. The pattern appears to keep its shape as it moves down the guide. However, as they propagate down the line, they induce currents in the guide walls, at right angles to the magnetic field.
Slots that do not noticeably interrupt wall current, do not radiate.
Microwave Components[edit | edit source]
Coupling Energy into a Waveguide
Probe or capacitive coupling acts like a 1/4 Marconi antenna. The probe, which might be the center conductor of a coaxial cable, is positioned 1/4 from the end of the guide. Since a total inversion occurs when the wave reflects, it adds in phase with the coupled signal.
The probe can be tapered to handle wideband signals. TE modes are generated if the probe is placed in the wide dimension of the guide, while TM modes are produced when the probe is placed in the narrow sidewall.
Loop or magnetic coupling creates magnetic fields that are launched from the antenna. The loop may be placed anywhere the magnetic field exists.
Aperture or slot coupling occurs when a slot is cut in the maximum of the electric or magnetic field area
Bends & Twists
The twist section is used to change between horizontal and vertical polarization.
Tees
Shunt tee - The signal at port C is the vector sum of ports A and B if they are used as inputs. If port C is used as the input, the power is evenly split between A and B.
Series Tee - Using the top port as the input, the power will b evenly split between A and B however, they will be anti phase.
Hybrid Tee - If A and B are used as the inputs, port C will be the vector sum and port D will be the vector difference. If C is the input, the energy will be evenly split between A and B. This device is often used to connect a transmitter and receiver to the same antenna. The antenna is at port B, the transmitter at C, the receiver at D, and a matched load at A.
Tuners
If the reactive stub is < 1/4 in the waveguide, it acts like a capacitor. If it is > 1/4 in the waveguide, it acts like an inductor. If it is 1/4 in the waveguide, it acts like an LC resonant circuit where the Q is proportional to the post diameter.
Tuning is sometimes done to minimize the amount of signal reflected from a waveguide component. This has a significant effect on the reflection coefficient and VSWR (voltage standing wave ratio). The effect of these things can be plotted and observed on a Smith Chart.
Terminators
All of the energy travelling down a waveguide must be absorbed in order to prevent reflections. This is accomplished by placing a resistor in the center of the guide where the electric field intensity is the greatest.
A short circuit is used if reflections are required.
A variable attenuator can be constructed by repositioning the absorbing material in the electric field.
Directional Couplers
Microwave Cavities[edit | edit source]
The dimensions of a microwave cavity must be some multiple of 1/2 l, and the Q may be as high as 100,000.
Energy is coupled into the cavity by means of a probe, loop, slot, or electron beam.
Conventional tubes have constant velocity beams and vary the number of electrons emitted to modulate the beam intensity. Microwave tubes emit a constant stream of electrons and vary their velocity to modulate the beam intensity.
Two Cavity Klystron
An electron beam is created at the cathode and passed by the buncher cavity. The RF energy coupled into the cavity causes the beam velocity to vary, thus causing the electrons to bunch. Energy is coupled to the catcher cavity when the beam passes its port. The net result is that the RF energy may be amplified by a factor of 1000.
The klystron acts as a high Q narrowband amplifier. It may have more bunching cavities to increase the gain or the cavities may be staggered tuned to increase the bandwidth.
Reflex Klystron
The reflex klystron has a single cavity that acts as both buncher and catcher. The beam is passed by the cavity, bunched, repelled and passed by the cavity a second time, and the absorbed in the sidewalls. It is necessary to turn on the repeller voltage prior to turning on the anode supply, otherwise the tube will self-destruct.
The reflex klystron is used as a low power, low efficiency, variable frequency oscillator. The operating frequency is adjusted by changing the cavity volume.
Magnetron
The magnetron is a high power microwave oscillator that has found widespread use in radar, radio beacon, and microwave oven applications.
The cylindrical cathode is surrounded by the anode, which has several resonant cavities. The entire assembly is placed in an intense right magnetic field running parallel to the cathode axis. This field causes an electron emitted from the cathode to follow a curved path on its way to the anode. However, the electron passes cavities on the route and so looses energy, causing it to fall back towards the cathode. The cathode repels the falling electron forcing it back towards the anode. This process continues ad infinitum. Electron bunching occurs each time the beam passes a cavity.
The critical magnetic field is that which allows the electron to just graze the anode. If the field intensity falls below this value, oscillation will cease. The dominant or π mode occurs when the polarity on adjacent poles is 180o apart. This causes the phase focusing effect where electrons are bunched in adjacent cavities. The beam shift around the interior is some integer multiple of the wavelength.
To prevent the bunched electrons to skip some cavities thus creating spurious modes, every second pole is strapped together. The output is taken from one of the cavities via a probe antenna. The magnetron can be mechanically tuned by about 5%.
The continuous power output can be as high as 25 kW, but with low duty cycle pulsing [.001] the peak output can be in the mega watt range.
TWT
Traveling wave tubes have a higher bandwidth but lower Q than klystrons. The RF signal traveling a helical path around the beam causes the beam to bunch. This in turn reinforces the RF signal causing amplification.
It can be used as a low power [30 mW], low noise amplifier with about a bandwidth of about one octave. Medium power devices operate at about 25 watts. High-powered devices can be pulsed at about 100 kW.
TWTs are used as broadband amplifiers and repeaters in TV, radar and satellite applications. It may be frequency or amplitude modulated.
Microwave Semiconductors[edit | edit source]
Gunn Diodes
The Gunn diode is not a diode in the truest sense because it does not contain a semiconductor junction. It is simply a piece of N-type gallium arsenide.
Normally the mobility of electrons increases as the electric field increases in a semiconductor. In this device, there is a range where the mobility of the electrons actually decreases as the electric field increases. Essentially the current falls as the voltage rises. This means that for a narrow range, the device exhibits a negative resistance. This is a very unstable situation and the device has a tendency to oscillate when biased in this region. The actual frequency of oscillation is dependent on the physical size of the semiconductor and occurs when the electron transit time is equal to one oscillation period.
Pin Diodes
PIN diodes are used as high frequency switches. The have very little junction capacitance and a very low forward voltage drop.
Microwave Measurements[edit | edit source]
Reflections in a waveguide are undesirable. They send power back to the source, which may ultimately damage the signal source, and they create standing waves.
Standing Waves
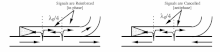
If waves are allowed to reflect from a microwave device, the incident and reflected waves will interact to create a standing wave. This is somewhat similar to the vibration of a stringed instrument.
The reflection coefficient is defined as the ratio of the reflected and incident voltage.
The ratio of maximum to minimum voltage of a standing wave is known as the VSWR (voltage standing wave ratio).
To eliminate the constant use of absolute magnitude bars, the reflection coefficient is often written as:
And since voltage is generally assumed to be the measured parameter:
- or
The physical distance between two consecutive minimums corresponds to one-half the guide wavelength
The VSWR can take on any value between 1 and ∞.
If VSWR = ∞, total reflection occurs. Ideally for a matched load, VSWR = 1 and there are no reflections. In practice, it is generally not cost effective to try to reduce the VSWR below 1.1.
Smith Chart
All values on the Smith chart are normalized to the characteristic impedance of the line.
Impedances are described by circles on a Smith chart.
This peculiar plotting method has a number of benefits. For one thing, the center of the chart corresponds to 1+1j. Consequently, it can be used to characterize any normalized transmission environment.
Furthermore, the SWR appears as a circle in the chart.
The normalized impedance is located at the intersection of SWR circle and reflection coefficient phase angle.
Review Questions
Quick Quiz
- 1. The magnetic field in a waveguide must terminate [normally, tangentially] on the conductor.
- 2. The [phase, guide] velocity in a waveguide can exceed the speed of light.
- 3. In a waveguide the electric field must terminate [normally, tangentially] on the conductor.
- 4. TM waves can be generated by placing a probe antenna in the [narrow, broad] side of a waveguide.
- 5. A [shunt, series, hybrid] tee is typically used to connect a transmitter and receiver to the same antenna.
- 6. When capacitively coupling energy into a waveguide, the probe is placed [1/4, 1/2, 1] away from the end plate.
- 7. A reactive stub acts like a capacitor when it is inserted [more, less] than 1/4 into the guide.
- 8. A TE wave has an impedance [greater, less] than 120 π ohms.
- 9. [TE, TM, TEM] waves cannot propagate in a waveguide.
- 10. The subscript in TEab denotes the number of [quarter, half, complete] cycles which appear in the a and b dimensions of the waveguide.
- 11. The dominant waveguide mode is [TE01, TE10, TE11].
- 12. The speed at which energy travels down a waveguide is known as the [group, phase] velocity.
- 13. The cutoff wavelength represents the [highest, lowest] frequency that can propagate down a waveguide.
- 14. The [shunt, series, hybrid] tee evenly splits power between two branches, but the outputs are phase inverted with respect to each other.
- 15. The [shunt, series, hybrid] tee is used to couple a transmitter and receiver to the same antenna.
- 16. The [magnetron, TWT] is a microwave oscillator.
- 17. The [reflex klystron, TWT] is a microwave amplifier.
- 18. The magnetron [is, is not] a tube.
- 19. The klystron can be used as either an amplifier or an oscillator. [True, False]
- 20. The microwave tubes modulate the electron beam [magnitude, velocity].
- 21. TWTs use buncher cavities to modulate the beam. [True, False]
Analytical Questions
- 1. A rectangular waveguide has the following characteristics:
Internal dimensions: 10.16 x 22.86 mm Feed: 10.5 GHz gunn diode
Determine if:
- a) If a TE20 wave will propagate
- b) If a TE10 wave will propagate
- c) The dominant mode guide wavelength
- d) The dominant mode group velocity
- e) The dominant mode phase velocity
- f) The dominant mode wave impedance
- g) Explain how you would measure the guide wavelength.
Composition Questions
- 1. Sketch the cross section of a two-hole directional coupler and discuss its operation.
- 2. Sketch the cross section of a magnetron and discuss its operation.
- 3. Sketch the TE10 mode in a rectangular waveguide, and show the position of all of the radiating and non-radiating slots.