Color Theory/Color gradient
| A Wikibookian believes this page should be split into smaller pages with a narrower subtopic. You can help by splitting this big page into smaller ones. Please make sure to follow the naming policy. Dividing books into smaller sections can provide more focus and allow each one to do one thing well, which benefits everyone. |
Theory[edit | edit source]

Introduction[edit | edit source]
- Your Friendly Guide to Colors in Data Visualisation by Lisa Charlotte Rost
- Playing with Gradient by rockraikar
- gimp concepts : gradients
- Ultra Fractal Gradient Hints by Janet Parke
- Image gradient at wikipedia
- Color gradient at wikipedia
- w3schools : css3 gradients
- gradients by Alan Gibson
- domain coloring
- DomainColoring by Emilia Petrisor
- dynamicmath : domain-coloring
- dctools by Juan Carlos Ponce Campuzano
- domain_coloring ( gnuplot)
Types of color gradient[edit | edit source]
Color gradients can be named by :
- dimension
- color bit depth
- color model: hsv[1]
- number of segments of gradient
- function used to create gradient
- special input values ( NAN, no data, high or low out-of-range values)[2][3]
- Number of colors
- number type, range and precision
- perceptual uniformity[4]
- monotonic
- Monotonic in hue
- Monotonic in saturation
- Monotonic in luminance
Dimension[edit | edit source]
1D[edit | edit source]
Here color of pixel is proportional to 1D variable. For example in 2D space ( complex plane where point z = x+y*i) :
- position with respect to x-axis of Cartesian coordinate system : x
- distance to origin : r=abs(z)
- potential[5]
- complex angle angle=arg(z)
- percepually uniform[6]
An example of a function to return a color that is linearly between two given colors:
colorA = [0, 0, 255] # blue colorB = [255, 0, 0] # red function get_gradient_color(val): # 'val' must be between 0 and 1 for i in [1,2,3]: color[i] = colorA[i] + val * (colorB[i] - colorA[i]) return color
-
1D gradient with color proportional to x
-
1D gradient with color proportional to radius
-
1D gradient with color proportional to angle
-
Hue circle for complex function plots
Code
- continous gradient
2D[edit | edit source]

ƒ(x) =(x2 − 1)(x − 2 − i)2/(x2 + 2 + 2i). The hue represents the function argument, while the saturation represents the magnitude.
Because color can be treated as more than 1D value it is used to represent more than one ( real or 1D) variable. For example :
- Robert Munafo uses 2 values from HSV model of color [7][8][9]
- John J. G. Savard uses own function [10][11]
- Domain coloring is a technique for visualizing functions of a complex variable
- matrixlab : rgb-images in MAtlab
- animated-contours from d3js.org
- Multiwave coloring for Mandelbrot by Paul Derbyshire
- 2D colormap by Gerrit[12]:
- The angle of the final iterate is most naturally mapped to hue, which has the matching topology of a circle
- the number of iterations is mapped to saturation and value (colorspace is 3D, at least for most humans).
' panomand/src/dll/fbmandel.bas
' https://www.unilim.fr/pages_perso/jean.debord/panoramic/mandel/panoramic_mandel.htm
' PANOMAND is an open source software for plotting Mandelbrot and Julia sets. It is written in two BASIC dialects: PANORAMIC and FreeBASIC
' by Jean Debord
' a simplified version of R Munafo's algorithm
' Color is defined in HSV space, according to Robert Munafo
' (http://mrob.com/pub/muency/color.html): the value V is
' computed from the distance estimator, while the hue H and
' saturation S are computed from the iteration number.
function MdbCol(byval Iter as integer, _
byval mz as double, _
byref dz as Complex) as integer
' Computes the color of a point
' Iter = iteration count
' mz = modulus of z at iteration Iter
' dz = derivative at iteration Iter
if Iter = Max_Iter then return &HFFFFFF
dim as double lmz, mdz, Dist, Dwell, DScale, Angle, Radius, Q, H, S, V
dim as integer R, G, B
lmz = log(mz)
mdz = CAbs(dz)
' Determine Value (luminosity) from Distance Estimator
V = 1
if mdz > 0 then
Dist = pp * mz * lmz / mdz
DScale = log(Dist / ScaleFact) / Lnp + Dist_Fact
if DScale < -8 then
V = 0
elseif DScale < 0 then
V = 1 + DScale / 8
end if
end if
' Determine Hue and Saturation from Continuous Dwell
Dwell = Iter - log(lmz) / Lnp + LLE
Q = log(abs(Dwell)) * AbsColor
if Q < 0.5 then
Q = 1 - 1.5 * Q
Angle = 1 - Q
else
Q = 1.5 * Q - 0.5
Angle = Q
end if
Radius = sqr(Q)
if (Iter mod 2 = 1) and (Color_Fact > 0) then
V = 0.85 * V
Radius = 0.667 * Radius
end if
H = frac(Angle * 10)
S = frac(Radius)
HSVtoRGB H * 360, S, V, R, G, B
return rgb(R, G, B)
end function
3D[edit | edit source]
- Hans Lundmark page[13]
Color model[edit | edit source]
The quality of 16-bit linear RGB is about equal to 12-bit sRGB (= nonlinear RGB), beacause linear color results in disproportionately more samples near white and fewer near black.
-
RGB and RGBA image
Types :
- RGB is for the display
- CMYK is for printing
- other ( HSV, HSL, ...) are for choosing color, processing
RGB[edit | edit source]
- RGB = "linear" color space
- sRGB
- sRGB = standard RGB. SRGBColorSpace (“srgb”) refers to the color space defined by the Rec. 709 primaries, D65 white point, and nonlinear sRGB transfer functions.
- The sRGB Linear space is the same as sRGB except that the transfer function is linear-light (there is no gamma-encoding
HSV[edit | edit source]
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <complex.h> // http://pubs.opengroup.org/onlinepubs/009604499/basedefs/complex.h.html
/*
based on
c++ program from :
http://commons.wikimedia.org/wiki/File:Color_complex_plot.jpg
by Claudio Rocchini
gcc d.c -lm -Wall
http://en.wikipedia.org/wiki/Domain_coloring
*/
const double PI = 3.1415926535897932384626433832795;
const double E = 2.7182818284590452353602874713527;
/*
complex domain coloring
Given a complex number z=re^{ i \theta},
hue represents the argument ( phase, theta ),
sat and value represents the modulus
*/
int GiveHSV( double complex z, double HSVcolor[3] )
{
//The HSV, or HSB, model describes colors in terms of hue, saturation, and value (brightness).
// hue = f(argument(z))
//hue values range from .. to ..
double a = carg(z); //
while(a<0) a += 2*PI; a /= 2*PI;
// radius of z
double m = cabs(z); //
double ranges = 0;
double rangee = 1;
while(m>rangee){
ranges = rangee;
rangee *= E;
}
double k = (m-ranges)/(rangee-ranges);
// saturation = g(abs(z))
double sat = k<0.5 ? k*2: 1 - (k-0.5)*2;
sat = 1 - pow( (1-sat), 3);
sat = 0.4 + sat*0.6;
// value = h(abs(z))
double val = k<0.5 ? k*2: 1 - (k-0.5)*2;
val = 1 - val;
val = 1 - pow( (1-val), 3);
val = 0.6 + val*0.4;
HSVcolor[0]= a;
HSVcolor[1]= sat;
HSVcolor[2]= val;
return 0;
}
int GiveRGBfromHSV( double HSVcolor[3], unsigned char RGBcolor[3] ) {
double r,g,b;
double h; double s; double v;
h=HSVcolor[0]; // hue
s=HSVcolor[1]; // saturation;
v = HSVcolor[2]; // = value;
if(s==0)
r = g = b = v;
else {
if(h==1) h = 0;
double z = floor(h*6);
int i = (int)z;
double f = (h*6 - z);
double p = v*(1-s);
double q = v*(1-s*f);
double t = v*(1-s*(1-f));
switch(i){
case 0: r=v; g=t; b=p; break;
case 1: r=q; g=v; b=p; break;
case 2: r=p; g=v; b=t; break;
case 3: r=p; g=q; b=v; break;
case 4: r=t; g=p; b=v; break;
case 5: r=v; g=p; b=q; break;
}
}
int c;
c = (int)(256*r); if(c>255) c = 255; RGBcolor[0] = c;
c = (int)(256*g); if(c>255) c = 255; RGBcolor[1] = c;
c = (int)(256*b); if(c>255) c = 255; RGBcolor[2] = c;
return 0;
}
int GiveRGBColor( double complex z, unsigned char RGBcolor[3])
{
static double HSVcolor[3];
GiveHSV( z, HSVcolor );
GiveRGBfromHSV(HSVcolor,RGBcolor);
return 0;
}
//
double complex fun(double complex c ){
return (cpow(c,2)-1)*cpow(c-2.0- I,2)/(cpow(c,2)+2+2*I);} //
int main(){
// screen (integer ) coordinate
const int dimx = 800; const int dimy = 800;
// world ( double) coordinate
const double reMin = -2; const double reMax = 2;
const double imMin = -2; const double imMax = 2;
//
double stepX=(imMax-imMin)/(dimy-1);
double stepY=(reMax-reMin)/(dimx-1);
static unsigned char RGBcolor[3];
FILE * fp;
char *filename ="complex.ppm";
fp = fopen(filename,"wb");
fprintf(fp,"P6\n%d %d\n255\n",dimx,dimy);
int i,j;
for(j=0;j<dimy;++j){
double im = imMax - j*stepX;
for(i=0;i<dimx;++i){
double re = reMax - i*stepY;
double complex z= re + im*I; //
double complex v = fun(z); //
GiveRGBColor( v, RGBcolor);
fwrite(RGBcolor,1,3,fp);
}
}
fclose(fp);
printf("OK - file %s saved\n", filename);
return 0;
}
In Basic :
' /panomand/src/dll/hsvtorgb.bas
' https://www.unilim.fr/pages_perso/jean.debord/panoramic/mandel/panoramic_mandel.htm
' PANOMAND is an open source software for plotting Mandelbrot and Julia sets. It is written in two BASIC dialects: PANORAMIC and FreeBASIC
' by Jean Debord
sub HSVtoRGB(byref H as double, _
byref S as double, _
byref V as double, _
byref R as integer, _
byref G as integer, _
byref B as integer)
' Convert RGB to HSV
' Adapted from http://www.cs.rit.edu/~ncs/color/t_convert.html
' R, G, B values are from 0 to 255
' H = [0..360], S = [0..1], V = [0..1]
' if S = 0, then H = -1 (undefined)
if S = 0 then ' achromatic (grey)
R = V * 255
G = R
B = R
exit sub
end if
dim as integer I
dim as double Z, F, P, Q, T
dim as double RR, GG, BB
Z = H / 60 ' sector 0 to 5
I = int(Z)
F = frac(Z)
P = V * (1 - S)
Q = V * (1 - S * F)
T = V * (1 - S * (1 - F))
select case I
case 0
RR = V
GG = T
BB = P
case 1
RR = Q
GG = V
BB = P
case 2
RR = P
GG = V
BB = T
case 3
RR = P
GG = Q
BB = V
case 4
RR = T
GG = P
BB = V
case 5
RR = V
GG = P
BB = Q
end select
R = RR * 255
G = GG * 255
B = BB * 255
end sub
Interpolating function[edit | edit source]
- One can use any function in each segment of gradient
- Output of function is scaled to range of color component
- interpolation between colors can be:
- lerp = Linear intERPolation, in sRGB color space
- nonlinear (quadratic, ...) classic in Photoshop[15]
- linear color space interpolation: convert keys from sRGB to float Linear, lerp between them, convert back into fixed point sRGB
- perceptual color space interpolation ( OKlab): convert keys from sRGB to float Linear, then into Oklab, lerp between them, convert back into float Linear, then back into fixed point sRGB.[16]
the tail of gradient Oklab evaluation function code by Aras Pranckevičius:
// to-Linear -> to-Oklab -> lerp -> to-Linear -> to-sRGB
float3 ca = pix_to_float(m_Keys[idx]);
float3 cb = pix_to_float(m_Keys[idx+1]);
ca = sRGB_to_Linear(ca);
cb = sRGB_to_Linear(cb);
ca = Linear_sRGB_to_OkLab_Ref(ca);
cb = Linear_sRGB_to_OkLab_Ref(cb);
float3 c = lerp(ca, cb, a);
c = OkLab_to_Linear_sRGB_Ref(c);
c = Linear_to_sRGB(c);
return float_to_pix(c);
In CSS interpolation between two color values takes place by executing the following steps:[17]
- (if required) converting them to a given color space which will be referred to as the interpolation color space below
- (if required) re-inserting carried-forward values in the converted colors
- (if required) fixing up the hues, depending on the selected <hue-interpolation-method>
- premultiplication of the color components
- linearly interpolating each component of the computed value of the color separately
- undoing premultiplication
Example 36. To interpolate:[18]
- in the Lab color space
- the two colors: rgb(76% 62% 03%/0.4) and color(display-p3 0.84 0.19 0.72/0.6)
- they are first converted to lab: lab(66.927% 4.873 68.622/0.4) lab(53.503% 82.672 -33.901/0.6)
- premultiplication: then the L, a and b coordinates are premultiplied before interpolation: [26.771% 1.949 27.449] and [32.102% 49.603 -20.341].
- Interpolation: The midpoint of linearly interpolating these would be [29.4365% 25.776 3.554] which,
- premultiplication is undone: with an alpha value of 0.5, which gives lab(58.873% 51.552 7.108) / 0.5)
Number of colors[edit | edit source]
Number of color is determined by color depth : from 2 colors to 16 mln of colors.
-
6-bit RGB uniform palette with black borders
-
Image:6-bit RGB uniform palette
-
256 VGA color gradient
See also
- 16-bit (rgb-565) color name definitions in c by Nic Newdigate
- About RGB565 and how to convert into it November 14, 2018 by Thomas Barth
Repetition and offset[edit | edit source]
Direct repetition :
Color is proportional to position <0;1> of color in color gradient. if position > 1 then we have repetition of colors. it maybe useful
Mirror repetition :
"colorCycleMirror - This will reflect the colour gradient so that it cycles smoothly " [19]
Offset :
How to use color gradients in computer programs[edit | edit source]
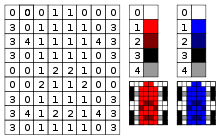
First find what format of color you need in your program.[20][21]
Ways of making gradient :
- gradient functions
- gradient files
"Lookup tables (LUTs) are an excellent technique for optimizing the evaluation of functions that are expensive to compute and inexpensive to cache. ... For data requests that fall between the table's samples, an interpolation algorithm can generate reasonable approximations by averaging nearby samples."[26]
CLUT image[edit | edit source]
One can use CLUT image a a source of the gradient[27][28]
convert input.pgm -level 0,65532 clut.ppm -interpolate integer -clut -depth 8 output.png
CLUT Array[edit | edit source]
python[edit | edit source]
# http://jtauber.com/blog/2008/05/18/creating_gradients_programmatically_in_python/
# Creating Gradients Programmatically in Python by James Tauber
import sys
def write_png(filename, width, height, rgb_func):
import zlib
import struct
import array
def output_chunk(out, chunk_type, data):
out.write(struct.pack("!I", len(data)))
out.write(chunk_type)
out.write(data)
checksum = zlib.crc32(data, zlib.crc32(chunk_type))
out.write(struct.pack("!I", checksum))
def get_data(width, height, rgb_func):
fw = float(width)
fh = float(height)
compressor = zlib.compressobj()
data = array.array("B")
for y in range(height):
data.append(0)
fy = float(y)
for x in range(width):
fx = float(x)
data.extend([int(v * 255) for v in rgb_func(fx / fw, fy / fh)])
compressed = compressor.compress(data.tostring())
flushed = compressor.flush()
return compressed + flushed
out = open(filename, "w")
out.write(struct.pack("8B", 137, 80, 78, 71, 13, 10, 26, 10))
output_chunk(out, "IHDR", struct.pack("!2I5B", width, height, 8, 2, 0, 0, 0))
output_chunk(out, "IDAT", get_data(width, height, rgb_func))
output_chunk(out, "IEND", "")
out.close()
def linear_gradient(start_value, stop_value, start_offset=0.0, stop_offset=1.0):
return lambda offset: (start_value + ((offset - start_offset) / (stop_offset - start_offset) * (stop_value - start_value))) / 255.0
def gradient(DATA):
def gradient_function(x, y):
initial_offset = 0.0
for offset, start, end in DATA:
if y < offset:
r = linear_gradient(start[0], end[0], initial_offset, offset)(y)
g = linear_gradient(start[1], end[1], initial_offset, offset)(y)
b = linear_gradient(start[2], end[2], initial_offset, offset)(y)
return r, g, b
initial_offset = offset
return gradient_function
## EXAMPLES
# normally you would make these with width=1 but below I've made them 50
# so you can more easily see the result
# body background from jtauber.com and quisition.com
write_png("test1.png", 50, 143, gradient([
(1.0, (0xA1, 0xA1, 0xA1), (0xDF, 0xDF, 0xDF)),
]))
# header background similar to that on jtauber.com
write_png("test2.png", 50, 90, gradient([
(0.43, (0xBF, 0x94, 0xC0), (0x4C, 0x26, 0x4C)), # top
(0.85, (0x4C, 0x26, 0x4C), (0x27, 0x13, 0x27)), # bottom
(1.0, (0x66, 0x66, 0x66), (0xFF, 0xFF, 0xFF)), # shadow
]))
# header background from pinax
write_png("test3.png", 50, 80, gradient([
(0.72, (0x00, 0x26, 0x4D), (0x00, 0x40, 0x80)),
(1.0, (0x00, 0x40, 0x80), (0x00, 0x6C, 0xCF)), # glow
]))
# form input background from pinax
write_png("test4.png", 50, 25, gradient([
(0.33, (0xDD, 0xDD, 0xDD), (0xF3, 0xF3, 0xF3)), # top-shadow
(1.0, (0xF3, 0xF3, 0xF3), (0xF3, 0xF3, 0xF3)),
]))
perl[edit | edit source]
# Perl code
# http://www.angelfire.com/d20/roll_d3_for_this/mandel-highorder/mandel-high.pl
# from perl High-order Mandelbrot program.
# Written by Christopher Thomas.
# Picture palette info.
my ($palsize);
my (@palette);
if(0)
{
# Light/dark colour banded palette.
# NOTE: This looks ugly, probably because the dark colours look muddy.
$palsize = 16;
@palette =
( " 255 0 0", " 0 112 112", " 255 128 0", " 0 0 128",
" 224 224 0", " 64 0 96", " 0 255 0", " 96 0 64",
" 0 224 224", " 128 0 0", " 0 0 255", " 128 64 0",
" 128 0 192", " 112 112 0", " 192 0 128", " 0 128 0" );
}
else
{
# 8-colour rainbow palette.
$palsize = 8;
@palette =
( " 255 0 0", " 255 128 0",
" 224 224 0", " 0 255 0",
" 0 224 224", " 0 0 255",
" 128 0 192", " 192 0 128" );
}
Conversions :
- between FractInt and Fractal eXtreme palettes [29]
lists:
Gradient functions[edit | edit source]
Name:
- coloring function
types

Examples :
- in JS using mandel.js[35] by Christopher Williams[36]
- Javascript using jQuery [37]
- C++ function by Richel Bilderbeek [38]
- Multiwave coloring for Mandelbrot[39]
- histogram colouring [40]
- Dave Green's `cubehelix' colour scheme
- css gradients
- stackoverflow question: how-to-create-colour-gradient-in-python
- complex_plot from Arb library and description
glsl[edit | edit source]
// https://www.shadertoy.com/view/lsd3zN
// sRGB demo by Tom Forsyth
// https://medium.com/@tomforsyth/the-srgb-learning-curve-773b7f68cf7a
//////////////////////////////////////////////////////////
//
// Illustration of the precision distribution of linear
// and sRGB formats.
//
// A ramp of 64 shades of each colour is shown to
// emphasise the distribution of banding in each format.
// Real formats of course have 256 shades.
//
// The leftmost bar of each colour is a linear format
// As you can see, although this format is linear in
// "photons per second", the difference in shades between
// the darker bands is far more obvious to the eye than
// the difference between the brighter bands. Thus,
// although linear space is a good place to do maths,
// when stored in a buffer the distribution of precision
// is poorly matched to the eye's preception of brightness.
//
// The middle bar of each colour is an sRGB format.
// While this is a strange non-linear format, and doing
// maths in it is not a good idea, it is an excellent
// format for storing "picturelike" data. You can see
// that the change in perceived brightness between adjacent
// bands is very uniform across the entire range of
// brightnesses, meaning that it has a distribution of
// precision that matches the eye's perception very well.
//
// The rightmost bar of each colour is a gamma 2.2 bar.
// This is not directly supported by hardware, and is there
// to illustrate that although it is quite similar to sRGB,
// there are significant differences between them, and
// care must be taken if trying to approximate one with
// the other. In general, it's not worth the very small
// performance difference.
//
//////////////////////////////////////////////////////////
// Taken from D3DX_DXGIFormatConvert.inl
float D3DX_FLOAT_to_SRGB ( float val )
{
if( val < 0.0031308 )
val *= 12.92;
else
val = 1.055 * pow(val,1.0/2.4) - 0.055;
return val;
}
// Taken from D3DX_DXGIFormatConvert.inl
// Technically this is not bit-exact - that requires a look-up table,
// but it's accurate enough for our purposes here.
float D3DX_SRGB_to_FLOAT(float val)
{
if( val < 0.04045 )
val /= 12.92;
else
val = pow((val + 0.055)/1.055,2.4);
return val;
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = fragCoord.xy / iResolution.xy;
float yShade = uv.y;
int colCol = int(floor(uv.x*4.0));
float fraction = uv.x*4.0 - float(colCol);
int colRamp = int(floor(fraction * 3.1));
// Make the basic colour.
vec3 baseCol;
if ( colCol == 0 )
{
baseCol = vec3(yShade,yShade,yShade); // white
}
else if ( colCol == 1 )
{
baseCol = vec3(yShade*0.6,yShade,0.0); // light green
}
else if ( colCol == 2 )
{
baseCol = vec3(yShade,yShade*0.5,yShade*0.2); // bronzeish
}
else
{
baseCol = vec3(yShade*0.5,0.0,yShade); // purple
}
// Artificially quantise to emphasise precision distribution
float shadeSteps = 64.0;
baseCol = (1.0/shadeSteps) * floor ( baseCol * shadeSteps );
// Now interpret that value as if it was a value stored in a texture of various formats.
vec3 linearCol;
if ( colRamp == 0 )
{
// Linear texture
linearCol = baseCol;
}
else if ( colRamp == 1 )
{
// sRGB texture
linearCol.x = D3DX_SRGB_to_FLOAT ( baseCol.x );
linearCol.y = D3DX_SRGB_to_FLOAT ( baseCol.y );
linearCol.z = D3DX_SRGB_to_FLOAT ( baseCol.z );
}
else if ( colRamp == 2 )
{
// 2.2 gamma for illustration
linearCol.x = pow ( baseCol.x, 2.2 );
linearCol.y = pow ( baseCol.y, 2.2 );
linearCol.z = pow ( baseCol.z, 2.2 );
}
else
{
// Separator.
linearCol = vec3(0.0,0.0,0.0);
}
// But then assume the display we're outputting to is gamma 2.2
float displayGamma = 2.2;
fragColor.x = pow ( linearCol.x, 1.0/displayGamma );
fragColor.y = pow ( linearCol.y, 1.0/displayGamma );
fragColor.z = pow ( linearCol.z, 1.0/displayGamma );
fragColor.w = 1.0;
}
HSV gradient[edit | edit source]
- explanation by Robert P. Munafo[41]
- Basic code and images by Jean Debord[42]
- c programs by Curtis T McMullen [43]
Linear RGB gradient with 6 segments[edit | edit source]
- rainbow gradient
-
2D RGB profile
-
2D HSV profile
-
3D RGB profile
Rainbow gradient
- in scientific computing
Here gradient consists from 6 segments. In each segment only one RGB component of color is changed using linear function.
Delphi version[edit | edit source]
// Delphi version by Witold J.Janik with help Andrzeja Wąsika from [pl.comp.lang.delphi]
// [i] changes from [iMin] to [iMax]
function GiveRainbowColor(iMin, iMax, i: Integer): TColor;
var
m: Double;
r, g, b, mt: Byte;
begin
m := (i - iMin)/(iMax - iMin + 1) * 6;
mt := (round(frac(m)*$FF));
case Trunc(m) of
0: begin
R := $FF;
G := mt;
B := 0;
end;
1: begin
R := $FF - mt;
G := $FF;
B := 0;
end;
2: begin
R := 0;
G := $FF;
B := mt;
end;
3: begin
R := 0;
G := $FF - mt;
B := $FF;
end;
4: begin
R := mt;
G := 0;
B := $FF;
end;
5: begin
R := $FF;
G := 0;
B := $FF - mt;
end;
end; // case
Result := rgb(R,G,B);
end;
/////
C version[edit | edit source]
Input of function are 2 variables :
- position of color in gradient, (a normalized float between 0.0 and 1.0 )
- color as an array of RGB components ( integer without sign from 0 to 255 )
This function does not use direct outoput ( void) but changes input variables color. One can use it this way:
GiveRainbowColor(0.25,color);
/* based on Delphi function by Witold J.Janik */
void GiveRainbowColor(double position,unsigned char c[])
{
/* if position > 1 then we have repetition of colors it maybe useful */
if (position>1.0){if (position-(int)position==0.0)position=1.0; else position=position-(int)position;}
unsigned char nmax=6; /* number of color segments */
double m=nmax* position;
int n=(int)m; // integer of m
double f=m-n; // fraction of m
unsigned char t=(int)(f*255);
switch( n){
case 0: {
c[0] = 255;
c[1] = t;
c[2] = 0;
break;
};
case 1: {
c[0] = 255 - t;
c[1] = 255;
c[2] = 0;
break;
};
case 2: {
c[0] = 0;
c[1] = 255;
c[2] = t;
break;
};
case 3: {
c[0] = 0;
c[1] = 255 - t;
c[2] = 255;
break;
};
case 4: {
c[0] = t;
c[1] = 0;
c[2] = 255;
break;
};
case 5: {
c[0] = 255;
c[1] = 0;
c[2] = 255 - t;
break;
};
default: {
c[0] = 255;
c[1] = 0;
c[2] = 0;
break;
};
}; // case
}
Cpp version[edit | edit source]
// C++ version
// here are some my modification but the main code is the same
// as in Witold J.Janik code
//
Uint32 GiveRainbowColor(double position)
// this function gives 1D linear RGB color gradient
// color is proportional to position
// position <0;1>
// position means position of color in color gradient
{
if (position>1)position=position-int(position);
// if position > 1 then we have repetition of colors
// it maybe useful
Uint8 R, G, B;// byte
int nmax=6;// number of color bars
double m=nmax* position;
int n=int(m); // integer of m
double f=m-n; // fraction of m
Uint8 t=int(f*255);
switch( n){
case 0: {
R = 255;
G = t;
B = 0;
break;
};
case 1: {
R = 255 - t;
G = 255;
B = 0;
break;
};
case 2: {
R = 0;
G = 255;
B = t;
break;
};
case 3: {
R = 0;
G = 255 - t;
B = 255;
break;
};
case 4: {
R = t;
G = 0;
B = 255;
break;
};
case 5: {
R = 255;
G = 0;
B = 255 - t;
break;
};
}; // case
return (R << 16) | (G << 8) | B;
}
Sine based gradient[edit | edit source]
"The idea is to change the color based on a sine wave. This gives a nice smooth gradient effect (although it’s not linear, which is not a requirement anyway). By changing the frequency of the RGB components (we could theoretically work with other color spaces such as HSV) we can get various gradients. Also, we can also play with the phase of each color component, creating a “shifting” effect. The basic implementation of such a gradient can be implemented like so:"
/*
http://blogs.microsoft.co.il/pavely/2013/11/12/color-gradient-generator/
*/
public Color[] GenerateColors(int number) {
var colors = new List<Color>(number);
double step = MaxAngle / number;
for(int i = 0; i < number; ++i) {
var r = (Math.Sin(FreqRed * i * step + PhaseRed) + 1) * .5;
var g = (Math.Sin(FreqGreen * i * step + PhaseGreen) + 1) * .5;
var b = (Math.Sin(FreqBlue * i * step + PhaseBlue) + 1) * .5;
colors.Add(Color.FromRgb((byte)(r * 255), (byte)(g * 255), (byte)(b * 255)));
}
return colors.ToArray();
}
"Where:
- the Freq* are the frequencies of the respective RGB colors
- Phase* are the phase shift values.
Note that all calculations are done with floating point numbers (ranging from 0.0 to 1.0), converting to a WPF Color structure (in this case) at the very end. This is simply convenient, as we’re working with trigonometric functions, which like floating point numbers rather than integers. The result is normalized to the range 0 to 1, as the sine function produces results from –1 to 1, so we add one to get a range of 0 to 2 and finally divide by 2 to get to the desired range."[44]
cubehelix[edit | edit source]
- Cubehelix gradient
-
2D RGB profile
-
3D RGB profile
cubehelix gradient
/*
GNUPLOT - stdfn.h
Copyright 1986 - 1993, 1998, 2004 Thomas Williams, Colin Kelley
*/
#ifndef clip_to_01
#define clip_to_01(val) \
((val) < 0 ? 0 : (val) > 1 ? 1 : (val))
#endif
/*
input : position
output : c array ( rgb color)
the colour scheme spirals (as a squashed helix) around the diagonal of the RGB colour cube
https://arxiv.org/abs/1108.5083
A colour scheme for the display of astronomical intensity images by D. A. Green
*/
void GiveCubehelixColor(double position, unsigned char c[]){
/* GNUPLOT - color.h
* Petr Mikulik, December 1998 -- June 1999
* Copyright: open source as much as possible
*/
// t_sm_palette
/* gamma for gray scale and cubehelix palettes only */
double gamma = 1.5;
/* control parameters for the cubehelix palette scheme */
//set palette cubehelix start 0.5 cycles -1.5 saturation 1
//set palette gamma 1.5
double cubehelix_start = 0.5; /* offset (radians) from colorwheel 0 */
double cubehelix_cycles = -1.5; /* number of times round the colorwheel */
double cubehelix_saturation = 1.0; /* color saturation */
double r,g,b;
double gray = position;
/*
Petr Mikulik, December 1998 -- June 1999
* Copyright: open source as much as possible
*/
// /* Map gray in [0,1] to color components according to colorMode */
// function color_components_from_gray
// from gnuplot/src/getcolor.c
double phi, a;
phi = 2. * M_PI * (cubehelix_start/3. + gray * cubehelix_cycles);
// gamma correction
if (gamma != 1.0) gray = pow(gray, 1./gamma);
a = cubehelix_saturation * gray * (1.-gray) / 2.;
// compute
r = gray + a * (-0.14861 * cos(phi) + 1.78277 * sin(phi));
g = gray + a * (-0.29227 * cos(phi) - 0.90649 * sin(phi));
b = gray + a * ( 1.97294 * cos(phi));
// normalize to [9,1] range
r = clip_to_01(r);
g = clip_to_01(g);
b = clip_to_01(b);
// change range to [0,255]
c[0] = (unsigned char) 255*r; //R
c[1] = (unsigned char) 255*g; // G
c[2] = (unsigned char) 255*b; // B
}
Gradient files[edit | edit source]
- Color Look-Up Table (CLUT)
File types for color gradient[edit | edit source]
There are special file types for color gradients:[45][46]
- The GIMP uses the files with .ggr extension [47]
- Fractint uses .map files [48]
- UltraFractal uses .ugr - These files can contain multiple gradients
- ual - old Ultra Fractal gradient file
- rgb, pal, gpf - gnuplot files
- The Matplotlib[49] colormap[50] is a lookup table[51]
- csv files
- maps in WHIP format ( Autodesk) by Paul Bourke
- Gnofract4D saves gradients only inside the graphic file, not as separate file.[52]
- MatLab
- Python
- R
- GMT
- QGIS
- Ncview
- Ferret
- Plotly
- Paraview
- VisIt
- Mathematica
- Surfer
- d3
- SKUA-GOCAD
- Petrel
- Fledermaus
- Qimera
- ImageJ
- Fiji
- Inkscape
- XML
- text
- SASS style sheet
- LESS - http://lesscss.org style sheet
- CSS - Cascading Style Sheet
csv files[edit | edit source]
a small table containing 33 values ( stored in a csv file) by Kenneth Moreland[53]
Scalar R G B
0 59 76 192
0.03125 68 90 204
0.0625 77 104 215
0.09375 87 117 225
0.125 98 130 234
0.15625 108 142 241
0.1875 119 154 247
0.21875 130 165 251
0.25 141 176 254
0.28125 152 185 255
0.3125 163 194 255
0.34375 174 201 253
0.375 184 208 249
0.40625 194 213 244
0.4375 204 217 238
0.46875 213 219 230
0.5 221 221 221
0.53125 229 216 209
0.5625 236 211 197
0.59375 241 204 185
0.625 245 196 173
0.65625 247 187 160
0.6875 247 177 148
0.71875 247 166 135
0.75 244 154 123
0.78125 241 141 111
0.8125 236 127 99
0.84375 229 112 88
0.875 222 96 77
0.90625 213 80 66
0.9375 203 62 56
0.96875 192 40 47
1 180 4 38CSS syntax[edit | edit source]
The default color space for mixing (and gradients) in CSS is oklab
Linear gradients[edit | edit source]
Non-repeating[edit | edit source]
Color gradients[56]
| Css code | description | Preview image |
|---|---|---|
linear-gradient(in lab to right, white, #01E)
|
CIE Lab gradient, which avoids the too-dark midpoint but has a significant purple cast; | |
linear-gradient(in srgb to right, white, #01E)
|
gamma-encoded sRGB gradient, is too dark at the midpoint, is a little desaturated, and has a slight purplish cast | |
linear-gradient(in Oklab to right, white, #01E)
|
Oklab gradient, giving a more perceptually uniform result with no purple cast at all | |
linear-gradient(to right, #a8c0ff, #3f2b96);
|
Ocean View | |
linear-gradient(in Oklab to right, #44C, #795)
|
Oklab gradient, perceptually uniform result with no purple cast at all | |
linear-gradient(in Oklab to right, black, #01E)
|
Oklab gradient, perceptually uniform result | |
linear-gradient(cyan, yellow);
|
||
linear-gradient(to left, violet, indigo, blue, green, yellow, orange, red);
|
VIBGYOR rainbow | |
linear-gradient(90deg, rgba(2,0,36,1) 0%, rgba(9,9,121,1) 35%, rgba(0,212,255,1) 100%);
|
black-to-white-gradient-in-each-space[57]
| description | Preview image |
|---|---|
| Oklab, perceptually uniform result | |
| oklch | |
| lab | |
| lch | |
| srgb | |
| srgb-linear | |
| hsl | |
| hwb | |
| xyz | |
| xyz-d50 | |
| xyz-d65 |
Repeating[edit | edit source]
| Code | Preview |
|---|---|
.gradient5 {
background-image: repeating-linear-gradient(cyan 0%, yellow 50%);
}
|
|
.gradient6 {
background-image: repeating-linear-gradient(to right, blue 0%, magenta 10%);
}
|
|
.gradient7 {
background-image: repeating-linear-gradient(60deg, cyan 0%, teal 23%, lime 31%);
}
|
conic[edit | edit source]
/* Hue wheel */ background: conic-gradient(red, yellow, lime, aqua, blue, magenta, red); border-radius: 50%
| Css code | description | Preview image |
|---|---|---|
conic-gradient(red, yellow, lime, aqua, blue, magenta, red); border-radius: 50%
|
color wheel |
Fractint map files[edit | edit source]
The default filetype extension for color-map files is ".MAP". These are ASCII text files. Consist of a series of RGB triplet values (one triplet per line, encoded as the red, green, and blue [RGB] components of the color). Color map ( or palette) is used as a colour look-up table[58] Default color map is in the Default.map file :
0 0 0 The default VGA color map 0 0 168 0 168 0 0 168 168 168 0 0 168 0 168 168 84 0 168 168 168 84 84 84 84 84 252 84 252 84 84 252 252 252 84 84 252 84 252 252 252 84 252 252 252 0 0 0 20 20 20 32 32 32 44 44 44 56 56 56 68 68 68 80 80 80 96 96 96 112 112 112 128 128 128 144 144 144 160 160 160 180 180 180 200 200 200 224 224 224 252 252 252 0 0 252 64 0 252 124 0 252 188 0 252 252 0 252 252 0 188 252 0 124 252 0 64 252 0 0 252 64 0 252 124 0 252 188 0 252 252 0 188 252 0 124 252 0 64 252 0 0 252 0 0 252 64 0 252 124 0 252 188 0 252 252 0 188 252 0 124 252 0 64 252 124 124 252 156 124 252 188 124 252 220 124 252 252 124 252 252 124 220 252 124 188 252 124 156 252 124 124 252 156 124 252 188 124 252 220 124 252 252 124 220 252 124 188 252 124 156 252 124 124 252 124 124 252 156 124 252 188 124 252 220 124 252 252 124 220 252 124 188 252 124 156 252 180 180 252 196 180 252 216 180 252 232 180 252 252 180 252 252 180 232 252 180 216 252 180 196 252 180 180 252 196 180 252 216 180 252 232 180 252 252 180 232 252 180 216 252 180 196 252 180 180 252 180 180 252 196 180 252 216 180 252 232 180 252 252 180 232 252 180 216 252 180 196 252 0 0 112 28 0 112 56 0 112 84 0 112 112 0 112 112 0 84 112 0 56 112 0 28 112 0 0 112 28 0 112 56 0 112 84 0 112 112 0 84 112 0 56 112 0 28 112 0 0 112 0 0 112 28 0 112 56 0 112 84 0 112 112 0 84 112 0 56 112 0 28 112 56 56 112 68 56 112 84 56 112 96 56 112 112 56 112 112 56 96 112 56 84 112 56 68 112 56 56 112 68 56 112 84 56 112 96 56 112 112 56 96 112 56 84 112 56 68 112 56 56 112 56 56 112 68 56 112 84 56 112 96 56 112 112 56 96 112 56 84 112 56 68 112 80 80 112 88 80 112 96 80 112 104 80 112 112 80 112 112 80 104 112 80 96 112 80 88 112 80 80 112 88 80 112 96 80 112 104 80 112 112 80 104 112 80 96 112 80 88 112 80 80 112 80 80 112 88 80 112 96 80 112 104 80 112 112 80 104 112 80 96 112 80 88 112 0 0 64 16 0 64 32 0 64 48 0 64 64 0 64 64 0 48 64 0 32 64 0 16 64 0 0 64 16 0 64 32 0 64 48 0 64 64 0 48 64 0 32 64 0 16 64 0 0 64 0 0 64 16 0 64 32 0 64 48 0 64 64 0 48 64 0 32 64 0 16 64 32 32 64 40 32 64 48 32 64 56 32 64 64 32 64 64 32 56 64 32 48 64 32 40 64 32 32 64 40 32 64 48 32 64 56 32 64 64 32 56 64 32 48 64 32 40 64 32 32 64 32 32 64 40 32 64 48 32 64 56 32 64 64 32 56 64 32 48 64 32 40 64 44 44 64 48 44 64 52 44 64 60 44 64 64 44 64 64 44 60 64 44 52 64 44 48 64 44 44 64 48 44 64 52 44 64 60 44 64 64 44 60 64 44 52 64 44 48 64 44 44 64 44 44 64 48 44 64 52 44 64 60 44 64 64 44 60 64 44 52 64 44 48 64 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Gimp/Inscape gpl files[edit | edit source]
Used by : Gimp, Inscape, Aseprite, Drawpile, Krita, MyPaint[59]
Syntax:
- ASCII files ( text files)[60]
- Comments must start with a #. In non-empty lines that don't, the first three tokens are parsed as numbers
- There is no alpha support
- GIMP Palette - it must be the first line of the file[61]
- Name: <name> - sets the name of the color palette.
- Columns: <number> - is just an indication for displaying the palette inside GIMP.
- # <comment> - comments must start with a #. All comments are ignored by GIMP.
- 0 0 0 Black - RGB values for the color followed by the color name
Source code of loader function [62]
GIMP palettes are stored using a special file format, in files with the extension .gpl.
Directory:
- ~/.config/GIMP/x.y/palettes/ directory (where x.y is the GIMP version number)
- ~/.config/inkscape/palettes/
GIMP Palette Name: Material Design Columns: 14 # 255 248 225 amber 50 255 236 179 amber 100 255 224 130 amber 200 255 213 79 amber 300 255 202 40 amber 400 255 193 7 amber 500 255 179 0 amber 600 255 160 0 amber 700 255 143 0 amber 800 255 111 0 amber 900 255 229 127 amber a100 255 215 64 amber a200 255 196 0 amber a400 255 171 0 amber a700 227 242 253 blue 50 187 222 251 blue 100 144 202 249 blue 200 100 181 246 blue 300 66 165 245 blue 400 33 150 243 blue 500 30 136 229 blue 600 25 118 210 blue 700 21 101 192 blue 800 13 71 161 blue 900 130 177 255 blue a100 68 138 255 blue a200 41 121 255 blue a400 41 98 255 blue a700 224 247 250 cyan 50 178 235 242 cyan 100 128 222 234 cyan 200 77 208 225 cyan 300 38 198 218 cyan 400 0 188 212 cyan 500 0 172 193 cyan 600 0 151 167 cyan 700 0 131 143 cyan 800 0 96 100 cyan 900 132 255 255 cyan a100 24 255 255 cyan a200 0 229 255 cyan a400 0 184 212 cyan a700 251 233 231 deep-orange 50 255 204 188 deep-orange 100 255 171 145 deep-orange 200 255 138 101 deep-orange 300 255 112 67 deep-orange 400 255 87 34 deep-orange 500 244 81 30 deep-orange 600 230 74 25 deep-orange 700 216 67 21 deep-orange 800 191 54 12 deep-orange 900 255 158 128 deep-orange a100 255 110 64 deep-orange a200 255 61 0 deep-orange a400 221 44 0 deep-orange a700 237 231 246 deep-purple 50 209 196 233 deep-purple 100 179 157 219 deep-purple 200 149 117 205 deep-purple 300 126 87 194 deep-purple 400 103 58 183 deep-purple 500 94 53 177 deep-purple 600 81 45 168 deep-purple 700 69 39 160 deep-purple 800 49 27 146 deep-purple 900 179 136 255 deep-purple a100 124 77 255 deep-purple a200 101 31 255 deep-purple a400 98 0 234 deep-purple a700 232 245 233 green 50 200 230 201 green 100 165 214 167 green 200 129 199 132 green 300 102 187 106 green 400 76 175 80 green 500 67 160 71 green 600 56 142 60 green 700 46 125 50 green 800 27 94 32 green 900 185 246 202 green a100 105 240 174 green a200 0 230 118 green a400 0 200 83 green a700 232 234 246 indigo 50 197 202 233 indigo 100 159 168 218 indigo 200 121 134 203 indigo 300 92 107 192 indigo 400 63 81 181 indigo 500 57 73 171 indigo 600 48 63 159 indigo 700 40 53 147 indigo 800 26 35 126 indigo 900 140 158 255 indigo a100 83 109 254 indigo a200 61 90 254 indigo a400 48 79 254 indigo a700 225 245 254 light-blue 50 179 229 252 light-blue 100 129 212 250 light-blue 200 79 195 247 light-blue 300 41 182 246 light-blue 400 3 169 244 light-blue 500 3 155 229 light-blue 600 2 136 209 light-blue 700 2 119 189 light-blue 800 1 87 155 light-blue 900 128 216 255 light-blue a100 64 196 255 light-blue a200 0 176 255 light-blue a400 0 145 234 light-blue a700 241 248 233 light-green 50 220 237 200 light-green 100 197 225 165 light-green 200 174 213 129 light-green 300 156 204 101 light-green 400 139 195 74 light-green 500 124 179 66 light-green 600 104 159 56 light-green 700 85 139 47 light-green 800 51 105 30 light-green 900 204 255 144 light-green a100 178 255 89 light-green a200 118 255 3 light-green a400 100 221 23 light-green a700 249 251 231 lime 50 240 244 195 lime 100 230 238 156 lime 200 220 231 117 lime 300 212 225 87 lime 400 205 220 57 lime 500 192 202 51 lime 600 175 180 43 lime 700 158 157 36 lime 800 130 119 23 lime 900 244 255 129 lime a100 238 255 65 lime a200 198 255 0 lime a400 174 234 0 lime a700 255 243 224 orange 50 255 224 178 orange 100 255 204 128 orange 200 255 183 77 orange 300 255 167 38 orange 400 255 152 0 orange 500 251 140 0 orange 600 245 124 0 orange 700 239 108 0 orange 800 230 81 0 orange 900 255 209 128 orange a100 255 171 64 orange a200 255 145 0 orange a400 255 109 0 orange a700 252 228 236 pink 50 248 187 208 pink 100 244 143 177 pink 200 240 98 146 pink 300 236 64 122 pink 400 233 30 99 pink 500 216 27 96 pink 600 194 24 91 pink 700 173 20 87 pink 800 136 14 79 pink 900 255 128 171 pink a100 255 64 129 pink a200 245 0 87 pink a400 197 17 98 pink a700 243 229 245 purple 50 225 190 231 purple 100 206 147 216 purple 200 186 104 200 purple 300 171 71 188 purple 400 156 39 176 purple 500 142 36 170 purple 600 123 31 162 purple 700 106 27 154 purple 800 74 20 140 purple 900 234 128 252 purple a100 224 64 251 purple a200 213 0 249 purple a400 170 0 255 purple a700 255 235 238 red 50 255 205 210 red 100 239 154 154 red 200 229 115 115 red 300 239 83 80 red 400 244 67 54 red 500 229 57 53 red 600 211 47 47 red 700 198 40 40 red 800 183 28 28 red 900 255 138 128 red a100 255 82 82 red a200 255 23 68 red a400 213 0 0 red a700 224 242 241 teal 50 178 223 219 teal 100 128 203 196 teal 200 77 182 172 teal 300 38 166 154 teal 400 0 150 136 teal 500 0 137 123 teal 600 0 121 107 teal 700 0 105 92 teal 800 0 77 64 teal 900 167 255 235 teal a100 100 255 218 teal a200 29 233 182 teal a400 0 191 165 teal a700 255 253 231 yellow 50 255 249 196 yellow 100 255 245 157 yellow 200 255 241 118 yellow 300 255 238 88 yellow 400 255 235 59 yellow 500 253 216 53 yellow 600 251 192 45 yellow 700 249 168 37 yellow 800 245 127 23 yellow 900 255 255 141 yellow a100 255 255 0 yellow a200 255 234 0 yellow a400 255 214 0 yellow a700 236 239 241 blue-grey 50 207 216 220 blue-grey 100 176 190 197 blue-grey 200 144 164 174 blue-grey 300 120 144 156 blue-grey 400 96 125 139 blue-grey 500 84 110 122 blue-grey 600 69 90 100 blue-grey 700 55 71 79 blue-grey 800 38 50 56 blue-grey 900 239 235 233 brown 50 215 204 200 brown 100 188 170 164 brown 200 161 136 127 brown 300 141 110 99 brown 400 121 85 72 brown 500 109 76 65 brown 600 93 64 55 brown 700 78 52 46 brown 800 62 39 35 brown 900 250 250 250 grey 50 245 245 245 grey 100 238 238 238 grey 200 224 224 224 grey 300 189 189 189 grey 400 158 158 158 grey 500 117 117 117 grey 600 97 97 97 grey 700 66 66 66 grey 800 33 33 33 grey 900 0 0 0 black 255 255 255 white
Gimp ggr files[edit | edit source]
"The gradients that are supplied with GIMP are stored in a system gradients folder. By default, gradients that you create are stored in a folder called gradients in your personal GIMP directory. Any gradient files (ending with the extension .ggr) found in one of these folders, will automatically be loaded when you start GIMP" ( from gimp doc ) Default gradients are in /usr/share/gimp/2.0/gradients directory ( check it in a window : Edit/preferences/directories)
Git repo
Gimp gradients can be created thru :
- GUI [63]
- manually in text editor ( use predefined gradients as a base)
- in own programs
Gimp gradient file format is described in:
- GIMP Application Reference Manual [64]
- source files :
- app/gradient.c and app/gradient_header.h for GIMP 1.3 version.[65]
- gimp-2.6.0/app/core/gimpgradient.c
Gimp Gradient Segment format :
typedef struct {
gdouble left, middle, right;
GimpGradientColor left_color_type;
GimpRGB left_color;
GimpGradientColor right_color_type;
GimpRGB right_color;
GimpGradientSegmentType type; /* Segment's blending function */
GimpGradientSegmentColor color; /* Segment's coloring type */
GimpGradientSegment *prev;
GimpGradientSegment *next;
} GimpGradientSegment;
In GimpConfig style format:[66]
<proposal>
# GIMP Gradient file
(GimpGradient "Abstract 1"
(segment 0.000000 0.286311 0.572621
(left-color (gimp-rgba 0.269543 0.259267 1.000000 1.000000))
(right-color (gimp-rgba 0.215635 0.407414 0.984953 1.000000))
(blending-function linear)
(coloring-type rgb))
(segment ...)
...
(segment ...))
</proposal>
GIMP Gradient Name: GMT_hot 3 0.000000 0.187500 0.375000 0.000000 0.000000 0.000000 1.000000 1.000000 0.000000 0.000000 1.000000 0 0 0.375000 0.562500 0.750000 1.000000 0.000000 0.000000 1.000000 1.000000 1.000000 0.000000 1.000000 0 0 0.750000 0.875000 1.000000 1.000000 1.000000 0.000000 1.000000 1.000000 1.000000 1.000000 1.000000 0 0
First line says it is a gimp gradient file.
Second line is a gradient's name.
Third line tells the number of segments in the gradient.
Each line following defines the property of each segment in following order :"[68]
- position of left stoppoint
- position of middle point
- position of right stoppoint
- R for left stoppoint
- G for left stoppoint
- B for left stoppoint
- A for left stoppoint
- R for right stoppoint
- G for right stoppoint
- B for right stoppoint
- A for right stoppoint
- Blending function constant
- coloring type constant
There are only two constants at the end of each line:
- the blending function constant of the segment (apparently 0=Linear, 1=Curved, 2=Sinusoidal, 3=Spherical (increasing), 4=Spherical (decreasing))
- the coloring type constant of the segment (probably 0=RGB, 1=HSV (counter-clockwise hue), 2=HSV (clockwise hue)[69]
json[edit | edit source]
links[edit | edit source]
- cpp code by Patrick Ross
- Reading gimp ggr files in python by Ned Batchelder
- Python Pil library functions for reading GIMP gradient files ( in file GimpGradientFile.py)
- perl scripts to convert gimp-1.2.x palettes and gradients into a 1.3 form by Jeff Trefftzs
- Gimp Python plugin: make-gradient.py by Giuseppe Conte
- gimp gradient files - lisp code from Polypen by Yannick Gingras
- Perl functions from GIMP pdb - gradient.pdb
- stackoverflow : javascript-color-gradient
- c pseudocode and js code by Christopher Williams
- Lode's Computer Graphics Tutorial : Light and Color
- bruce lindbloom : color equations
Collections of gradients / colormaps[edit | edit source]
- gradcentral
- Cpt-city
- gimp gradients (ggr files) are in directory : /usr/share/gimp/2.0/gradients/
- The COLOURlovers site hosts a million 5-colour palettes in several formats
- thi.ng
- SciVisColor
- Fabio Crameri: scientific colourmaps in provided in all major formats
programs[edit | edit source]
- [1] Color tools for design systems
- gnuplot
- mdigi tools color: Color tools for the web listed alphabetically
- The CCC-Tool[70] is a general tool for the creation, analyzing and testing of colormaps with the effort to minimize the needed interaction components.
- image magic[71]
- OpenCV library
- python
- colorAide A library to aid in using colors
- coloria Tools for color research
- colour-science: Colour is an open-source Python package providing a comprehensive number of algorithms and datasets for colour science.
- colour = color representations manipulation library (RGB, HSL, web, ...) by Valentin Lab
- njsmith: colorspacious: A powerful, accurate, and easy-to-use Python library for doing colorspace conversions
- Colour is an open-source Python package providing a comprehensive number of algorithms and datasets for colour science. It is freely available under the New BSD License terms. Colour is an affiliated project of NumFOCUS, a 501(c)(3) nonprofit in the United States.
- matplotlib
- matplotlib: viscm A tool for visualizing and designing colormaps using colorspacious and matplotlib
- math3d : sphere colormap
- VIVID GRADIENT GENERATOR TOOL by learn ui design
- paletton- color scheme designer and generator
- Image Magic
color convert[edit | edit source]
- qConv.com - The quick converter and color manager. The powerful color database for designers and agencies.
- hextoral color converter
- colormine color-converter
- ColorSpace: C++ library for converting between color spaces and comparing colors by Nicolae Berendea
- farver: High Performance Colourspace Manipulation in R. Src code in c++. It provides an interface to a modified version of the ColorSpace C++ library.
split your hexadecimal color code into 3 values, that could be treated as RGB vectors (RGB decimals) ( from hextoral)
color gradient convert[edit | edit source]
- ggr2glsl is a simple utility to convert GIMP gradient files to GLSL functions.
- gradient-converter-apophysis-to-kalles-fraktaler
tests[edit | edit source]
Test your :
- monitor ( gamut)
- graphic card
- printer
- own
Test your color abilities[edit | edit source]
- The X-Rite Color Challenge and Hue Test
- The FM100 Hue Test is an easy-to-administer test and a highly effective method for evaluating an individual's ability to discern color.
How to choose color gradient ?[edit | edit source]
- How to Choose Colours Procedurally (Algorithms) 29 Jul, 2012 by Herman Tulleken
- perceptually-smooth-multi-color-linear-gradients by Matt DesLauriers Jan 25, 2021
- Nonlinear Color Scales for Interactive Exploration by Young Hyun
- gencolormap
- Color Maps for Scientific Visualization by Kenneth Moreland
- In Search of a Perfect Colormap by Peter Karpov
- Good Colour Maps: How to Design Them by Peter Kovesi
- Rainbow Color Map Critiques: An Overview and Annotated Bibliography By Steve Eddins, MathWorks
- scivis tutorials
- Matteo Niccoli
- bids: Colormap recommendation
How to visualize/test/evaluate/compare colormaps?[edit | edit source]
In python to visualize matplotlib built-in colormaps:
python -m viscm view jet
To visualize one of viscm colormaps:
python -m viscm view path/to/colormap_script.py
In gnuplot use test command:
set palette rgbformulae 21,22,23
set terminal gif
set output 'p.gif'
test palette
Results: 2D profiles of each color channel
One can also make curve through RGB colorspace:
R code
# Install the released version from CRAN:
install.packages("pals")
# Loading required package: pals
require(pals)
# The palette is converted to RGB or LUV coordinates and plotted in a three-dimensional scatterplot. The LUV space is probably better, but it is easier to tweak colors by hand in RGB space.
pal.cube(cubehelix)
pal.cube(coolwarm)
Tips:
- A good discrete palette has distinct colors
- A good continuous colormap does not show boundaries between colors
See also
- How to evaluate and compare color maps by SEG
- pals: R programming language package to evaluate colormaps
- colorcet test image
- matplotlib color map manipultions
- Kenneth Moreland: color-advice
- David Johnstone: lch-lab-colour-gradient-picker
- ccc tool
- scivis color : color moves app
- color brewer colomaps
How to make perceptually uniform gradient?[edit | edit source]
- How to generate a perceptually uniform gradient with CAM16UCS colour model?
- stackoverflow qestion: more-perceptually-uniform-colormaps
- CMasher: Scientific, perceptually uniform colormaps
- colorcet : Perceptually Uniform Colour Maps by Peter Kovesi
- matplotlib cmocean : Beautiful colormaps for oceanography. Most of the colormaps started from matplotlib colormaps, but have now been adjusted using the viscm tool to be perceptually uniform.
How to make colormap with maximum distinguishable colours?[edit | edit source]
- stackoverflow question: colormap-with-maximum-distinguishable-colours
- Colorgorical To generate a palette with n colors,
How to use special values in colormap?[edit | edit source]
How to Calculate the average color of an image ?[edit | edit source]
Averaging RGB should be correct assuming you do it in linear RGB. If your images are in sRGB, you can remove the gamma correction by doing something like the following for each of the R, G, and B components:
float sRGBToLinear(UInt8 component)
{
float tempComponent = (float)component / 255.0;
if (tempComponent <= 0.04045)
{
tempComponent = tempComponent / 12.92;
}
else
{
tempComponent = pow((tempComponent + 0.055) / (1.055), 2.4);
}
return tempComponent;
}
You can then average together all of the red values in the image, all of the green values in the image, and all of the blue values in the image after they've been run through the above conversion. You can then do the opposite conversion to get back to sRGB:
UInt8 linearRGBTosRGB(float component)
{
float tempComponent = 0.0;
if (component <= 0.00318308)
{
tempComponent = 12.92 * component;
}
else
{
tempComponent = 1.055 * pow(component, 1.0 / 2.4) - 0.055;
}
return (UInt8)(tempComponent * 255.0);
}
Note that alpha makes things slightly more complicated. If you're using premultiplied alpha, you can simply apply the above calculations for the average. If you're using straight alpha, you'll want to multiply each of the R, G, and B components by the alpha before doing the averaging.[74]
How to render light spectrum?[edit | edit source]
How to read(pick) color from the image ?[edit | edit source]
- Pick Color From Image by ginifab
- pick-a-color-from-an-image-using-canvas-and-javascript by nakome
- developer mozilla: getting_the_pixel_data_for_a_context
- How to get the pixel color from a canvas on click or mouse event with Javascript from ourcodeworld
How to read color gradient from image ?[edit | edit source]
- online
- color.adobe tool
- color-loom/ Colorloom is a tool developed by the Sculpting Vis Collaborative and inspired to mimic palette creation in the arts. The tool extracts a selection of hues from images and enables users to create continuous colormaps by dragging these extracted hues into a desired order, all within the same interface. These colormaps can be exported in a variety of formats for use in major visualization software.
How to extract color palette from image ?[edit | edit source]
- Colores.py—extract color palettes from your favorite images [75]
- Color Scheme Extraction[76]
- using Image Magic [77]
- using Gimp [78]
- "There is this small tool in fractalshades that interactively grabs a colormap from a line you draw on an image, the editor looks like the attached picture. Not perfect, but I found it useful (in the 'tools' section). The cmap can then be used in the program or exported for later use (for the time being, exports only to a txt format specific to this program.)" Geoffroy Billotey (GBillotey)[79]
How to extract ICC profile from the image file ?[edit | edit source]
Using Image Magic:[80]
convert photo.jpg profile.icc
How to view ICC profile ?
exiftool a.icc
Example output:
ExifTool Version Number : 12.40 File Name : vw1.icc Directory : . File Size : 548 bytes File Modification Date/Time : 2023:11:12 20:48:16+01:00 File Access Date/Time : 2023:11:12 20:48:47+01:00 File Inode Change Date/Time : 2023:11:12 20:48:16+01:00 File Permissions : -rw-rw-r-- File Type : ICC File Type Extension : icc MIME Type : application/vnd.iccprofile Profile CMM Type : Apple Computer Inc. Profile Version : 4.0.0 Profile Class : Display Device Profile Color Space Data : RGB Profile Connection Space : XYZ Profile Date Time : 2018:06:24 13:22:32 Profile File Signature : acsp Primary Platform : Apple Computer Inc. CMM Flags : Not Embedded, Independent Device Manufacturer : Unknown (OPPO) Device Model : Device Attributes : Reflective, Glossy, Positive, Color Rendering Intent : Perceptual Connection Space Illuminant : 0.9642 1 0.82491 Profile Creator : Apple Computer Inc. Profile ID : 0 Profile Description : Display P3 Profile Copyright : Copyright Apple Inc., 2017 Media White Point : 0.95045 1 1.08905 Red Matrix Column : 0.51512 0.2412 -0.00105 Green Matrix Column : 0.29198 0.69225 0.04189 Blue Matrix Column : 0.1571 0.06657 0.78407 Red Tone Reproduction Curve : (Binary data 32 bytes, use -b option to extract) Chromatic Adaptation : 1.04788 0.02292 -0.0502 0.02959 0.99048 -0.01706 -0.00923 0.01508 0.75168 Blue Tone Reproduction Curve : (Binary data 32 bytes, use -b option to extract) Green Tone Reproduction Curve : (Binary data 32 bytes, use -b option to extract)
How to find lighter and darker colors based on any initial color ?[edit | edit source]
- 0to255 a color tool by Shaun Chapman uses the lightness (L) scale from HSL
- stackoverflow : formula-to-determine-brightness-of-rgb-color
- stackoverflow : programmatically-lighten-or-darken-a-hex-color-or-rgb-and-blend-colors
- learnwebgl: model_color by C. Wayne Brown: To change a color (r,g,b) to make it lighter, move it closer to (1,1,1). To change a color (r,g,b) to make it darker, move it closer to (0,0,0).
// darker by C. Wayne Brown newR = R + (0-R)*t; // where t varies between 0 and 1 newG = G + (0-G)*t; // where t varies between 0 and 1 newB = B + (0-B)*t; // where t varies between 0 and 1 // lighter C. Wayne Brown newR = R + (1-R)*t; // where t varies between 0 and 1 newG = G + (1-G)*t; // where t varies between 0 and 1 newB = B + (1-B)*t; // where t varies between 0 and 1
How to remove gradient banding ?[edit | edit source]
How to generate and refine palettes of optimally distinct colors[edit | edit source]
How to simulating colors of the sky ?[edit | edit source]
How to make quality images?[edit | edit source]
Gradient contours[edit | edit source]
- description by Alan Gibson.[81]
Examples of beautiful gradients[edit | edit source]
- Mandelbrot 109 - Mandelflake by olbaid-st
- a slight motion in the colour gradient
See also[edit | edit source]
- Color_calibration
- Color correction
- Color terms
- Swatch Book = color palette in digital terminology, collection of material fragments in different colors, Paper color swatch book, Wool swatch book
- Image noise
- Commons Category:Color in computer graphics
- stackoverflow questions tagged gradient
- github topics
- scratchapixel: simulating-sky
- Color by Bruce MacEvoy
- The X-Rite Color Challenge and Hue Test
- colour lovers: Color/s, Pattern/s, Palette/s, Lover/s or stats
- gamma correction
- coloring algorithms
- perceptually uniform color space
- bruce lindbloom
- gradient maps by bjango: Gradient maps in Photoshop use brightness to assign corresponding colours taken from a gradient of your choice
References[edit | edit source]
- ↑ dsp.stackexchange question: why-do-we-use-the-hsv-colour-space-so-often-in-vision-and-image-processing
- ↑ stackoverflow question:how-can-i-plot-nan-values-as-a-special-color-with-imshow
- ↑ matplotlib: Colormap set_bad
- ↑ Completely Painless Programmer's Guide to XYZ, RGB, ICC, xyY, and TRCs by Elle Stone
- ↑ fractalforums.org: smooth-1d-coloring
- ↑ observablehq mjbo: perceptually-uniform-color-models
- ↑ R2.1/2.C(1/2) by Robert Munafo
- ↑ Color by Robert Munafo
- ↑ Mandelbrot and Julia sets with PANORAMIC and FreeBASIC By jdebord
- ↑ The Mandelbrot Function by John J. G. Savard
- ↑ The Mandelbrot Function 2 by John J. G. Savard
- ↑ fractalforums.org/: 2d-coloring
- ↑ Visualizing complex analytic functions using domain coloring by Hans Lundmark
- ↑ w3docs color-hwb
- ↑ New gradient interpolation options ( Last updated on May 24, 2023) from Adobe
- ↑ Optimizing Oklab gradients by Aras Pranckevičius.
- ↑ drafts csswg org: css-color-4
- ↑ drafts csswg.org: css-color-4
- ↑ The Fractal Explorer Pixel Bender filters by Tom Beddard
- ↑ What's Delphi TColor format? at ACASystems
- ↑ Delhi TColor at efg2.com
- ↑ wikipedia :Colour_look-up_table
- ↑ fractalforums : creating-a-good-palette-using-bezier-interpolation
- ↑ FracTest : palettes
- ↑ stefanbion : fraktal-generator and colormapping/
- ↑ nvidia gpu gems2 : using-lookup-tables-accelerate-color
- ↑ Paul Tol's notes
- ↑ gmic : color_presets
- ↑ Fractal Forums > Fractal Software > Fractal Programs > Windows Fractal Software > Fractal eXtreme > Converting between FractInt and Fractal eXtreme palettes
- ↑ stackoverflow question : smooth-spectrum-for-mandelbrot-set-rendering
- ↑ on-rainbows by Charlie Loyd
- ↑ Stefan Bion : color mapping
- ↑ stackoverflow question : which-color-gradient-is-used-to-color-mandelbrot-in-wikipedia
- ↑ Making annoying rainbows in javascript A tutorial by jim bumgardner
- ↑ mandel.js by Christopher Williams
- ↑ Custom Palettes by Christopher Williams
- ↑ Gradient jQuery plugin Posted by David Wees
- ↑ C++ function by Richel Bilderbeek
- ↑ Multiwave coloring for Mandelbrot
- ↑ histogram colouring is really streching (not true histogram)
- ↑ Color by Robert Munafo
- ↑ Mandelbrot and Julia sets with PANORAMIC and FreeBASIC By Jean Debord
- ↑ c programs by Curtis T McMullen
- ↑ color-gradient-generator by Pavel
- ↑ Color gradient file formats explained
- ↑ 29 Colour Map Formats... by Peter Kovesi
- ↑ GIMP add-ons: types, installation, management by Alexandre Prokoudine
- ↑ Fractint Palette Maps and map files
- ↑ matplotlib: colormap-manipulation
- ↑ matplotlib colormaps
- ↑ wikipedia: Lookup table
- ↑ gnofract4d manual
- ↑ kenneth moreland: color-maps
- ↑ w3.org docs : gradient
- ↑ stackoverflow question : how-is-a-css-gradient-path-calculated ?
- ↑ New functions, gradients, and hues in CSS colors (Level 4) by Smith 3 May 2023
- ↑ developer chrome articles: css-color-mix
- ↑ w:Colour look-up table
- ↑ About A collection of RGB color palettes for GIMP and Inkscape (but also Aseprite, Drawpile, Krita and MyPaint) by Dezmerean Robert
- ↑ stackoverflow question: gimp-palette-file-gpl-format-syntax
- ↑ Add custom color palettes to GIMP and Inkscape by Dezmerean Robert
- ↑ Source code of gimp load palette function
- ↑ gimp-gradient-editor-dialog doc
- ↑ GimpGradient doc at GIMP Application Reference Manual
- ↑ [Gimp-developer] Format of GIMP gradient files
- ↑ [Gimp-developer] Format of GIMP gradient files
- ↑ [Gimp-developer] Format of GIMP gradient files
- ↑ gpr format description by Vinay S Raikar
- ↑ Emulating ggr/GIMP gradient in JavaFx
- ↑ CCC-Tool
- ↑ imagemagick : gradient
- ↑ Dave Green's 'cubehelix' colour scheme
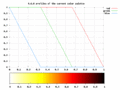
- ↑ Diverging Color Maps for Scientific Visualization - Kenneth Moreland
- ↑ computergraphics SE question: calculate-the-average-color-of-an-image
- ↑ extract color palletes from your favorite images by John Mangual
- ↑ algorithmia : create-a-custom-color-scheme-from-your-favorite-website/
- ↑ ImageMagick v6 Examples -- Color Quantization and Dithering
- ↑ Tool to extract palette / color table from image
- ↑ fractalforums.org : beautiful-and-effective-coloring-of-fractals
- ↑ rawpedia: how to extract and examine ICC profiles ?
- ↑ gradint contours by Alan Gibson


























![diverging[73]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/d1/3D_RGB_profile_of_the_Smooth_Cool_Warm_diverging_color_gradient_by_Kenneth_Moreland.png/120px-3D_RGB_profile_of_the_Smooth_Cool_Warm_diverging_color_gradient_by_Kenneth_Moreland.png)