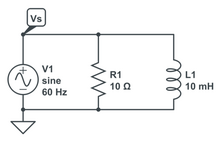
Parallel RL circuit for example 9 Given that the voltage source is defined by
V
s
(
t
)
=
120
2
c
o
s
(
377
t
+
120
∘
)
{\displaystyle V_{s}(t)=120{\sqrt {2}}cos(377t+120^{\circ })}
Parallel RL circuit marked up for analysis In a parallel circuit, all devices have the exact same voltage across them.
Knowns, Unknowns and Equations [ edit | edit source ] Knowns:
V
s
,
R
,
L
{\displaystyle V_{s},R,L}
Unknowns:
I
s
,
i
R
,
i
L
{\displaystyle I_{s},i_{R},i_{L}}
Equations:
V
s
(
t
)
=
R
∗
i
R
(
t
)
,
V
s
=
L
∗
d
d
t
i
L
(
t
)
,
i
R
(
t
)
+
i
L
(
t
)
−
I
s
(
t
)
=
0
{\displaystyle V_{s}(t)=R*i_{R}(t),V_{s}=L*{d \over dt}i_{L}(t),i_{R}(t)+i_{L}(t)-I_{s}(t)=0}
Saying the initial conditions are zero is impossible in this problem.
Look at the terminal relation:
V
s
=
V
L
=
L
∗
d
d
t
i
L
(
t
)
{\displaystyle V_{s}=V_{L}=L*{d \over dt}i_{L}(t)}
VS has a non-zero value at t=0+ . This means
d
d
t
i
L
(
t
)
=
V
s
/
L
{\displaystyle {d \over dt}i_{L}(t)=V_{s}/L}
+ ) = 0.
Evaluate the terminal relations in this order:
i
R
(
t
)
=
V
s
R
{\displaystyle i_{R}(t)={\frac {V_{s}}{R}}}
i
L
(
t
)
=
∫
V
s
L
d
t
{\displaystyle i_{L}(t)=\int {\frac {V_{s}}{L}}dt}
i
s
(
t
)
=
i
R
(
t
)
+
i
L
(
t
)
{\displaystyle i_{s}(t)=i_{R}(t)+i_{L}(t)}
phasor matlab solution of RL circuit .... m file
V
s
(
t
)
=
120
2
cos
(
377
t
+
2.09
)
{\displaystyle V_{s}(t)=120{\sqrt {2}}\cos(377t+2.09)}
R
=
10
{\displaystyle R=10}
L
=
.01
{\displaystyle L=.01}
i
R
=
12
2
cos
(
377
t
+
2.09
)
{\displaystyle i_{R}=12{\sqrt {2}}\cos(377t+2.09)}
i
L
=
∫
120
2
cos
(
377
t
+
2.09
)
.01
d
t
=
45
sin
(
377
t
+
2.09
)
+
C
1
{\displaystyle i_{L}=\int {\frac {120{\sqrt {2}}\cos(377t+2.09)}{.01}}dt=45\sin(377t+2.09)+C_{1}}
i
L
(
0
)
=
0
=
45
sin
(
2.09
)
+
C
1
{\displaystyle i_{L}(0)=0=45\sin(2.09)+C_{1}}
C
1
=
−
39
{\displaystyle C_{1}=-39}
i
L
=
45
sin
(
377
t
+
2.09
)
−
39
{\displaystyle i_{L}=45\sin(377t+2.09)-39}
I
s
(
t
)
=
12
2
cos
(
377
t
+
2.09
)
+
45
sin
(
377
t
+
2.09
)
−
39
{\displaystyle I_{s}(t)=12{\sqrt {2}}\cos(377t+2.09)+45\sin(377t+2.09)-39}
phasor math avoids trig! m-file The next step is to combine the answer into a single cos term with a phase shift so it can be compared to
i
L
{\displaystyle i_{L}}
i
R
{\displaystyle i_{R}}
The easiest method to combine the sin and cos terms is phasors.
Here is the phasor method. Notice the math is done in the phasor domain ... with imaginary numbers.
12
∗
2
∗
(
377
t
+
2.09
)
⇔
12
∗
2
c
o
s
(
2.09
)
+
j
12
∗
2
s
i
n
(
2.09
)
{\displaystyle 12*{\sqrt {2}}*(377t+2.09)\Leftrightarrow 12*{\sqrt {2}}cos(2.09)+j12*{\sqrt {2}}sin(2.09)}
45
s
i
n
(
377
t
+
2.09
)
⇔
45
∗
s
i
n
(
2.09
)
−
j
45
∗
c
o
s
(
2.09
)
{\displaystyle 45sin(377t+2.09)\Leftrightarrow 45*sin(2.09)-j45*cos(2.09)}
Now the numbers are in the phasor world. The next step is to add them all up.
I
s
=
48.1
∠
0.884
{\displaystyle \mathbb {I} _{s}=48.1\angle 0.884}
Now put back into the time domain:
I
s
=
48.1
cos
(
377
t
+
0.884
)
−
39
{\displaystyle I_{s}=48.1\cos(377t+0.884)-39}
i
R
=
V
s
/
R
{\displaystyle i_{R}=V_{s}/R}
i
L
=
∫
V
s
L
d
t
{\displaystyle i_{L}=\int {\frac {V_{s}}{L}}dt}
i
S
=
i
R
+
i
L
{\displaystyle i_{S}=i_{R}+i_{L}}
V
s
(
t
)
→
V
{\displaystyle V_{s}(t)\rightarrow \mathbb {V} }
V
=
V
m
∠
ϕ
{\displaystyle \mathbb {V} =V_{m}\angle \phi }
I
R
=
V
R
=
V
m
R
∠
ϕ
{\displaystyle \mathbb {I} _{R}={\frac {\mathbb {V} }{R}}={\frac {V_{m}}{R}}\angle \phi }
∫
V
s
(
t
)
d
t
→
V
j
ω
=
V
ω
∠
−
π
2
=
V
m
ω
∠
(
ϕ
−
π
2
)
{\displaystyle \int V_{s}(t)dt\rightarrow {\frac {\mathbb {V} }{j\omega }}={\frac {\mathbb {V} }{\omega }}\angle {\frac {-\pi }{2}}={\frac {V_{m}}{\omega }}\angle (\phi -{\frac {\pi }{2}})}
I
L
=
V
m
ω
L
∠
(
ϕ
−
π
2
)
{\displaystyle \mathbb {I} _{L}={\frac {V_{m}}{\omega L}}\angle (\phi -{\frac {\pi }{2}})}
I
S
=
V
m
R
∠
ϕ
+
V
m
ω
L
∠
(
ϕ
−
π
2
)
{\displaystyle \mathbb {I} _{S}={\frac {V_{m}}{R}}\angle \phi +{\frac {V_{m}}{\omega L}}\angle (\phi -{\frac {\pi }{2}})}
I
S
=
V
m
∗
1
R
2
+
1
(
L
ω
)
2
∠
(
ϕ
−
a
r
c
t
a
n
(
R
L
ω
)
)
{\displaystyle \mathbb {I} _{S}=V_{m}*{\sqrt {{\frac {1}{R^{2}}}+{\frac {1}{(L\omega )^{2}}}}}\angle (\phi -arctan({\frac {R}{L\omega }}))}
I
L
(
t
)
=
Re
(
I
L
e
j
ω
t
)
=
V
m
ω
L
∗
c
o
s
(
ω
t
+
ϕ
−
π
2
)
+
C
1
{\displaystyle I_{L}(t)=\operatorname {Re} (\mathbb {I} _{L}e^{j\omega t})={\frac {V_{m}}{\omega L}}*cos(\omega t+\phi -{\frac {\pi }{2}})+C_{1}}
I
s
(
t
)
=
Re
(
I
s
e
j
ω
t
)
=
V
m
1
R
2
+
1
(
L
ω
)
2
c
o
s
(
ω
t
+
ϕ
−
a
r
c
t
a
n
(
R
L
ω
)
)
+
C
1
{\displaystyle I_{s}(t)=\operatorname {Re} (\mathbb {I} _{s}e^{j\omega t})=V_{m}{\sqrt {{\frac {1}{R^{2}}}+{\frac {1}{(L\omega )^{2}}}}}cos(\omega t+\phi -arctan({\frac {R}{L\omega }}))+C_{1}}
I
R
(
t
)
=
Re
(
I
R
e
j
ω
t
)
=
V
m
R
c
o
s
(
ω
t
+
ϕ
)
{\displaystyle I_{R}(t)=\operatorname {Re} (\mathbb {I} _{R}e^{j\omega t})={\frac {V_{m}}{R}}cos(\omega t+\phi )}
I
L
{\displaystyle I_{L}}
doing problem using phasors rather than calculus m-filec there is no point in doing the math in the phasor domain if can solve in symbol form as above
i
r
(
t
)
=
120
∗
2
10
cos
(
377
t
+
2.09
)
=
17.0
c
o
s
(
377
t
+
2.09
)
{\displaystyle i_{r}(t)={\frac {120*{\sqrt {2}}}{10}}\cos(377t+2.09)=17.0cos(377t+2.09)}
i
L
(
t
)
=
120
∗
2
.01
∗
377
cos
(
377
t
+
2.09
−
π
2
)
+
C
2
=
45
cos
(
377
t
+
0.524
)
+
C
1
{\displaystyle i_{L}(t)={\frac {120*{\sqrt {2}}}{.01*377}}\cos(377t+2.09-{\frac {\pi }{2}})+C_{2}=45\cos(377t+0.524)+C_{1}}
0
=
45
cos
(
0.524
)
+
C
1
{\displaystyle 0=45\cos(0.524)+C_{1}}
C
1
=
−
39.0
{\displaystyle C_{1}=-39.0}
i
s
(
t
)
=
120
∗
2
∗
1
10
2
+
1
(
.01
∗
377
)
2
cos
(
377
t
+
2
∗
ϕ
3
−
arctan
(
10
.01
∗
377
)
)
−
39
{\displaystyle i_{s}(t)=120*{\sqrt {2}}*{\sqrt {{\frac {1}{10^{2}}}+{\frac {1}{(.01*377)^{2}}}}}\cos(377t+{\frac {2*\phi }{3}}-\arctan({\frac {10}{.01*377}}))-39}
i
s
(
t
)
=
48.1
cos
(
377
t
+
0.844
)
−
39
{\displaystyle i_{s}(t)=48.1\cos(377t+0.844)-39}
These are the same numbers as calculated with Calculus above ...
V
s
{\displaystyle Vs}
I
s
{\displaystyle I_{s}}
i
L
{\displaystyle i_{L}}
i
R
{\displaystyle i_{R}}
simulation are graphed below.
circuitlab.com simulation with the current into a device which produces 180° phase shift
Symbol
color
Equation
I
s
{\displaystyle I_{s}}
Brown
48.1
cos
(
377
t
+
50.6
∘
)
−
39
{\displaystyle 48.1\cos(377t+50.6^{\circ })-39}
i
L
{\displaystyle i_{L}}
Orange
45
cos
(
377
t
+
30
∘
)
−
39
{\displaystyle 45\cos(377t+30^{\circ })-39}
i
R
{\displaystyle i_{R}}
Example
17
cos
(
377
t
+
120
∘
)
{\displaystyle 17\cos(377t+120^{\circ })}
Vs</math>
Blue
170
cos
(
377
t
+
120
∘
)
{\displaystyle 170\cos(377t+120^{\circ })}
showing what happens when circuitlab skip initial=no ..
The simulation also shows that the integration constant is dependent upon the phase angle of the source.
The period above looks to be between 16ms and 17ms, closer to 17ms. This agrees with the formula:
ω
=
2
π
∗
f
{\displaystyle \omega =2\pi *f}
f
=
ω
2
π
{\displaystyle f={\frac {\omega }{2\pi }}}
T
=
1
f
=
2
π
ω
=
2
π
377
=
16.7
m
s
{\displaystyle T={\frac {1}{f}}={\frac {2\pi }{\omega }}={\frac {2\pi }{377}}=16.7ms}
The simulation magnitudes, if measured peak to peak match the doubled magnitudes of the numeric answers. The integration constant adds a DC bias which is negative in this case.
Voltage will always lead the current through an inductor (think of the terminal relationship or ELI) by
90
∘
,
π
2
{\displaystyle 90^{\circ },{\frac {\pi }{2}}}
1
4
{\displaystyle {\frac {1}{4}}}
The constants are going to add some DC power or real power to this analysis. Without knowing what they are, we can not compute their impact. So for now we stick with phasor domain power analysis:
V
s
=
120
2
∠
2.09
{\displaystyle \mathbb {V} _{s}=120{\sqrt {2}}\angle 2.09}
I
s
=
48.1
∠
0.884
{\displaystyle \mathbb {I} _{s}=48.1\angle 0.884}
I
s
∗
=
48.1
2
∠
−
0.884
{\displaystyle \mathbb {I} _{s}^{*}=48.1{\sqrt {2}}\angle -0.884}
if :
V
=
M
v
∠
ϕ
v
{\displaystyle \mathbb {V} =M_{v}\angle \phi _{v}\quad }
I
=
M
i
∠
ϕ
i
{\displaystyle \quad \mathbb {I} =M_{i}\angle \phi _{i}}
S
=
V
I
∗
=
M
v
M
i
2
∠
(
ϕ
v
−
ϕ
i
)
=
120
2
∗
48.1
2
∠
(
2.09
−
0.884
)
=
4081
∠
1.206
=
1456
+
3813
j
{\displaystyle \mathbb {S} =\mathbb {V} \mathbb {I} ^{*}={\frac {M_{v}M_{i}}{2}}\angle (\phi _{v}-\phi _{i})={\frac {120{\sqrt {2}}*48.1}{2}}\angle (2.09-0.884)=4081\angle 1.206=1456+3813j}
and
c
o
s
(
1.206
)
=
.357
{\displaystyle cos(1.206)=.357}
This is a bad power factor. The utility's apparent power is much larger than what the customer is willing to pay. Pure inductive loads as described are found in large motors in industrial settings where engineers working for industry are talking to engineers working for the power company. Power conditioners may be needed to bring this power factor back up closer to 1. The utility will charge based upon apparent power ... which is real $$$ for them.
Value
Units
Description
4081
{\displaystyle 4081}
volt-ampere vaapparent power what utility companies manage: peak power they design for, peak power they have to deliver
.357
{\displaystyle .357}
unitless power factor, ratio of real power to apparent power, ideally 1
1456
{\displaystyle 1456}
watt Wreal, average, active power ... what consumers want to pay for (watt-hours)
3813
{\displaystyle 3813}
volt-amp-reactive varreactive power ... why not all outlets in a room are on the same circuit breaker
ELI ... voltage leads the current through an inductor
Integration constants matter. Initial conditions matter. Phasors don't deal with them.
A purely inductive load connected to a power source is going to create a bad power factor.
If integration constants show up, and there is no differential equation, must compute the integration constants using initial conditions.
Phase angle of the source influences the integration constant.