Circuit Theory/Convolution Integral/Examples/example49/current

series LRC circuit ... find voltage across the resistor

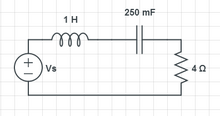
Given that the source voltage is (2t-3t²), find voltage across the resistor.

Here focused on finding current first:

Transfer Function

$H(s)={\frac {i}{V_{S}}}={\frac {1}{4+s+{\frac {1}{0.25s}}}}$

simplify(1/(4 + s + 1/(0.25*s)))

$H(s)={\frac {s}{s^{2}+4s+4}}$

Homogeneous Solution

solve(s^2 + 4.0*s + 4.0,s)

There are two equal roots at s = -2, so the solution has the form:

$i_{h}(t)=Ae^{-2t}+Bte^{-2t}+C_{1}$

Particular Solution

After a long time attached to a unit step function source, the inductor has shorted and the capacitor has opened. All the drop is across the capacitor. The current is zero.

$i_{p}=0$

Initial Conditions

So far the full equation is:

$i(t)=Ae^{-2t}+Bte^{-2t}+C_{1}$

Initial current through the series leg is zero because of the assumed initial conditions of the inductor. This means:

$i(0)=0=A+C_{1}$

Assuming the initial voltage across the capacitor is zero, then initial voltage drop has to be across the inductor.

$V_{L}(t)=L{di(t) \over dt}=(-2A+B)e^{-2t}-2Bte^{-2t}$

$V_{L}(0)=1=-2A+B$

After a long period of time, the current still has to be zero so:

$C_{1}=0$

This means that:

$A=0$

$B=1$

$i(t)=te^{-2t}$

$V_{r}(t)=4te^{-2t}$

The 4 is lost in the numerator of the transfer function if a transfer function is written for V_r initially. The 4 does not make it into the homogeneous solution. In second order analysis, never write a transfer function for a resistor.

Impulse Solution

Taking the derivative of the above get:

$V_{R}\delta (t)=4e^{-2t}-8te^{-2t}$

Convolution Integral

$V_{R}(t)=\int _{0}^{t}(4e^{-2(t-x)}-8(t-x)e^{-2(t-x)})(2x-3x^{2})dx$

f := (4*exp(-2*(t-x)) - 8*(t-x)exp(-2*(t-x)))*(2*x-3*x^2);
S :=int(f,x=0..t)

$V_{R}(t)=8-8e^{-2t}-10te^{-2t}-6t$

There will not be any constant since again, V_R(t) = 0 after a long time ... and the capacitor opens.