Circuit Theory/Convolution Integral/Examples/example49/Vc

series LRC circuit ... find voltage across the resistor

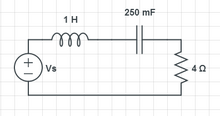
Given that the source voltage is (2t-3t²), find voltage across the resistor.

This is the V_c solution.

Outline:

Transfer Function

$H(s)={\frac {V_{C}}{V_{S}}}={\frac {\frac {1}{0.25s}}{4+s+{\frac {1}{0.25s}}}}$

simplify((1/(s*0.25))/(4 + s + 1/(0.25*s)))

$H(s)={\frac {4}{s^{2}+4s+4}}$

Homogeneous Solution

solve(s^2 + 4.0*s + 4.0,s)

There are two equal roots at s = -2, so the solution has the form:

$V_{C_{h}}(t)=Ae^{-2t}+Bte^{-2t}+C_{1}$

Particular Solution

After a long time attached to a unit step function source, the inductor has shorted and the capacitor has opened. All the drop is across the capacitor. The current is zero.

$V_{C_{p}}=1$

This also means that C₁ is still unknown.

Initial Conditions

So far the full equation is:

$V_{C}(t)=1+Ae^{-2t}+Bte^{-2t}+C_{1}$

At t = ∞ what is the B term's value?

limit(B*t*exp(-t),t = infinity)

Mupad says 0. So This means that at t = ∞:

$1=1+C_{1}$

$C_{1}=0$

Initial voltage across the capacitor is 0 so:

$0=1+A+C_{1}$

$A=-1$

Initial current through the series leg is zero because of the assumed initial conditions of the inductor. This means i(0) = 0, so:

$i(t)=C*{dV_{C}(t) \over dt}={\frac {1}{4}}((-2A+B)e^{-2t}-2Bte^{-2t})$

$0={\frac {1}{4}}(-2A+B)$

$B=2A$

$B=-2$

This means that i(t) =:

$i(t)={\frac {1}{4}}((-2(-1)+(-2))e^{-2t}-2(-2)te^{-2t})=te^{-2t}$

$V_{R}(t)=4*i(t)=4te^{-2t}$

Impulse Solution

Taking the derivative of the above get:

$V_{R}\delta (t)=4e^{-2t}-8te^{-2t}$

Convolution Integral

$V_{R}(t)=\int _{0}^{t}(4e^{-2(t-x)}-8(t-x)e^{-2(t-x)})(2x-3x^{2})dx$

f := (4*exp(-2*(t-x)) - 8*(t-x)exp(-2*(t-x)))*(2*x-3*x^2);
S :=int(f,x=0..t)

$V_{R}(t)=8-8e^{-2t}-10te^{-2t}-6t$

There will not be any constant since again, V_R(t) = 0 after a long time ... and the capacitor opens.